计及风电不确定性的多场景多时段安全约束机组组合解耦求解方法

吴 雄，何雯雯，李晓飞，麻 淞，刘炳文

（西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

随着新型电力系统的发展，风电机组装机容量在电力系统中的占比不断提高［1］。在大规模风电机组并网带来巨大的环境效益和经济效益的同时，风电的强波动性和不确定性［2］也给电力系统的调度运行带来了困难。在数学建模分析中，通常采用多场景刻画风电不确定性，随着场景数的增加，计及风电不确定性的安全约束机组组合（security-constrained unit commitment，SCUC）问题成为一个多场景多时段的大规模混合整数优化问题，该问题的求解难度较大［3］。

求解传统确定性的SCUC 问题是电力系统短期发电计划编排的核心环节，能够提升系统的节能性和经济性，使机组尽可能地运行在最佳工作点［4］，而大规模风电的接入给SCUC 问题带来了不确定变量，使得传统确定性SCUC 问题的可行域发生了改变。目前，关于计及风电不确定性的SCUC 问题的研究分为确定性和不确定性思想［5］。确定性思想需要在备用约束中考虑风电的全部备用，该思想过于保守，会增加电力系统的运行成本；不确定性思想主要集中于对风电随机性的研究。国内外学者对计及风电不确定性的SCUC 问题开展了广泛研究。文献［6］提出满足非预期约束条件的风电最优消纳全场景可行混合整数线性规划（mixed integer linear programming，MILP）模型及求解方法，但当风电场数量较多时，该方法存在求解规模较大的问题。文献［7］考虑新能源机组出力的随机性与电力系统负荷的波动性，为日前调度提供了一个具有可靠性指标的机会约束随机规划模型。文献［8］针对风电出力过程中难以对概率密度与分布进行建模的问题，提出一种基于非精确狄利克雷模型的分布鲁棒机组组合模型。文献［9］根据不确定集的离散性特点，针对大规模新能源机组接入电力系统的问题，提出适合离散型不确定集的鲁棒优化模型，但该模型的结果过于保守。文献［10］建立考虑风电出力模糊置信水平的机组组合模型，推导风电预测误差的可信性分布函数，并将模糊机会约束转化为等价约束，该方法适用于大规模电力系统。文献［11-13］提出基于地理区域分解的分布式SCUC 求解方法，虽然该方法降低了问题的复杂度，但是由于不同时段和不同场景之间是耦合的，求解时间较长，无法满足电网调度的实际需要。文献［14］提出对传统SCUC 问题的并行求解方法，但是未考虑新能源机组出力的波动性对电力系统运行产生的影响。

综上，本文针对计及风电不确定性的多场景多时段SCUC问题，提出一种基于目标级联分析（analytical target cascading，ATC）［1］算法的并行求解方法。首先，考虑随机场景与基准场景之间火电机组的爬坡耦合约束，在各子问题的模型中添加惩罚项和一致性约束，用于保证场景解耦的可行性，并对各场景的SCUC 问题进行并行计算；其次，为了进一步缩短求解时间，将解耦后的各场景SCUC 问题按照时段分解为几个较小时段的子问题，在各子问题的模型中添加惩罚项和一致性约束，以保证解的可行性，并对各子问题进行并行计算；然后，提出一种基于ATC算法的多场景多时段SCUC 并行求解方法；最后，通过算例分析验证所提方法的有效性。

1 多场景多时段解耦机制及数学模型

1.1 计及风电不确定性的多场景SCUC原始模型

由于风电出力具有不确定性，风电实际出力会在预测值附近波动，因此，将风电出力预测值设置为基准场景，将偏离预测值的风电出力值设置为随机场景。

以发电费用f最小为目标函数，即：

在随机场景和基准场景下，系统均需满足功率平衡、机组爬坡、线路潮流等约束，具体表达式如附录A式（A1）—（A18）所示。

1.2 多场景解耦机制

为便于描述以及更好地利用分布式算法的优点，将计及风电不确定性的SCUC 模型划分为基准场景和多个随机场景。以基准场景和随机场景m为例进行说明，为了确保解的可行性，在各场景的目标函数中添加惩罚项，并在模型中增加一致性约束。

电力系统需要时刻保持功率平衡，在风电出力波动的情况下，火电机组需要在规定时间内调整输出功率，以满足功率平衡条件，即在每个时段t内，随机场景m下的火电机组需要与基准场景下的火电机组满足爬坡耦合约束，如式（12）所示。火电机组的上下限出力限制如式（13）所示。火电机组在随机场景m和基准场景下的出力一致性约束如式（14）所示。火电机组在随机场景m和基准场景下的启停状态一致性约束如式（15）所示。ub，t，n(m，b)与ηb，t，n(m，b)、γb，t，n(m，b)的关系如式（16）所示。ub，t，n(b，m)与ηb，t，n(b，m)、γb，t，n(b，m)的关系如式（17）所示。

式中：t=1，2，…，T；n=1，2，…，N；下标“(m，b)”表示在随机场景m下求得的基准场景下的相应变量；下标“(b，m)”表示在基准场景下求得的随机场景m下的相应变量；ΔP为火电机组n的最大上爬坡速率；ΔP为火电机组n的最大下爬坡率；ub，t，n为t时段基准场景下火电机组n的启停状态变量，当火电机组n开启时其值为1，当火电机组n停机时其值为0；P为火电机组n的最小出力；P为火电机组n的最大出力。

1.3 多时段解耦机制

利用多场景解耦机制将原始的多场景SCUC 问题解耦为各单场景SCUC 问题，为进一步缩短求解时间，以计及风电不确定性的单场景SCUC 模型为例，分析适用于所有场景的多时段解耦机制。将SCUC 模型的整个时段划分为多个较小的连续子时段，不失一般性，如图1所示，将总时段划分为3个子时段，分别记为c-、c和c+，t1—tc+为时长是1 h 的时段，将对应的SCUC 子问题分别记为Sc-、Sc和Sc+。引入耦合时段［14］的概念，以分析2个连续子时段间的一致性条件，子时段c-与子时段c间的耦合时段为tc-+1，子时段c与子时段c+间的耦合时段为tc+1。

图1 时段解耦示意图Fig.1 Schematic diagram of period decomposition

多时段解耦机制采用与多场景解耦机制类似的策略，即为确保解的可行性，在邻接的子问题目标函数中添加惩罚项和一致性约束。SCUC 子问题的模型与传统集中式方法的SCUC 模型相同，将各连续SCUC 子问题间的时段耦合关联转换为一组共享变量，并用一致性约束的方式耦合各子问题模型。在各子问题间的耦合时段内，需保持一致性的变量包括火电机组出力、火电机组启停状态、风电机组出力以及火电机组需要达到的最小开机与最小停机时间。

火电机组在耦合时段内发电的一致性约束为：

式中：n=1，2，…，N；P为t时段火电机组n的出力；下标“(c-，c)”表示在子时段c-求得的子时段c的相应变量；下标“(c，c-)”表示在子时段c求得的子时段c-的相应变量；下标“(c，c+)”表示在子时段c求得的子时段c+的相应变量；下标“(c+，c)”表示在子时段c+求得的子时段c的相应变量。

风电机组在耦合时段内发电的一致性约束为：

式中：k=1，2，…，K；P为t时段风电机组k的出力。为了对2 个连续子时段之间的火电机组最小启停机时间进行建模，设开机变量T和停机变量分别表示火电机组n在子时段c-中最末时段内已持续开机、停机的时间。火电机组n在子时段c中需要达到的最小剩余开机时间T和停机时间分别为：

式中：n=1，2，…，N；T为火电机组n的最小开机时间；T为火电机组n的最小停机时间。

在子问题Sc中设置一个停机指示标志F，其值等于火电机组n在子时段c中第1 次停机的时间。利用大M 法［15］对火电机组n在子时段c中第1 个时段的停机情况进行建模。根据子问题Sc求得的火电机组n在子时段c-中需要达到的最小剩余开机时间为：

式中：n=1，2，…，N；M1为一个足够大的数。

同理，根据子问题Sc求得的火电机组n在子时段c-中需要达到的最小剩余停机时间TTh，Un(c，c-)为：

式中：n=1，2，…，N；F为子问题Sc中的开机指示标志；M2为一个足够大的数。

火电机组n在子问题Sc-与子问题Sc边界需要满足的最小开机、停机的一致性约束为：

式中：n=1，2，…，N；un为火电机组n的启停状态，当火电机组n开启时其值为1，当火电机组n停机时其值为0。

2 并行求解方法流程

本文基于ATC 算法提出同时进行多场景多时段解耦的并行求解方法。ATC是一种解决层次结构协调问题和分散式问题的算法［16］，该算法具有并行计算的优点且适用于大多数工程问题，因此常被用于解决大规模优化问题。ATC 算法原理如图2 所示，图中Sbc-、Sbc、Sbc+和Smc-、Smc、Smc+分别表示基准场景和随机场景m下的各子问题。ATC 算法的基本原理是，将整个优化问题分解为不同的子问题，利用一致性约束耦合各邻接子问题，引入协调器对各子问题一致性约束中的共享变量进行协调优化，使得可以对各子问题进行并行求解，直到满足收敛条件。在优化各子问题模型的同时，通过引入惩罚项使各子问题中的共享变量趋于一致，惩罚项通常用各种范数进行表示，本文使用增广拉格朗日罚函数来惩罚违反一致性约束的行为。

2.1 协调器数学模型

协调器数学模型以最小化子问题的共享变量差值为目标函数，如式（29）所示。将协调器中的共享变量组记为响应变量组，将各子问题的共享变量组记为目标变量组。

式中：h为迭代次数；ζh为第h次迭代时的拉格朗日乘子向量组；eh为第h次迭代时求得的响应变量组；yh为 第h次 迭 代 时 求 得 的 目 标 变 量 组；ρ为 惩 罚因子。

当协调器从各子问题中接收到目标变量组yh后，通过求解式（29）、（30）可得到更新后的响应变量组eh，并将eh传递至子问题数学模型。

拉格朗日乘子向量组的更新公式为：

并行求解方法的收敛条件为：

式中：ε为收敛精度。

2.2 基于增广拉格朗日函数的子问题数学模型

同一场景中各邻接子问题之间的共享变量包括在子问题边界需要达到的最小开机、停机时间以及耦合时段内的火电机组出力和风电机组出力。随机场景和基准场景之间的共享变量包括随机场景中的火电机组出力。不失一般性，假设将总时段划分为3 个子时段，即每个随机场景m和基准场景下均包括3个子问题，如图2所示。

利用紧凑模型表示各子问题。对于随机场景m，在其子问题的目标函数中加入增广拉格朗日惩罚项，在其子问题的模型中加入一致性约束。子问题的数学模型为：

2.3 并行算法求解流程

如果没有选取合适的初始化数据，ATC 算法就难以收敛，为此，本文提出一种初始化变量的方式。忽略邻接子问题之间的一致性约束与共享变量，此时各子问题均完全独立，对这些子问题进行并行求解。可行域示意图如图3 所示，对于原始的多场景多时段SCUC 问题，假设x1为实际最优解，x2为忽略邻接子问题之间一致性约束与共享变量的最优解，x3为任意选取的初始数据。实际的可行域常被包含于忽略一致性约束与共享变量的可行域中，否则SCUC 问题将无解。由于各子问题的数学模型中包含除一致性约束外的其他SCUC 约束，因此，所得到的结果x2可能不是可行解，但x2比任意选取的初始数据x3更加逼近实际最优解x1，因此，将x2作为ATC算法的初始化数据。

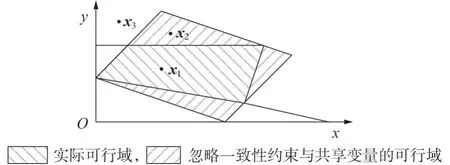
图3 可行域示意图Fig.3 Schematic diagram of feasible region

本文提出的多场景多时段解耦并行求解方法具体流程如下。

步骤1 输入网络及机组参数，设置变量初始值、拉格朗日乘子向量组初始值以及惩罚因子初始值。

步骤2 令迭代次数h=1。

步骤3 对各随机场景m与基准场景的子问题进行并行求解，并将其所得目标变量组yh向上反馈至协调器。

步骤4 协调器在接收到目标变量组yh后，通过求解式（29）、（30）得到更新后的响应变量组eh。

步骤5 判断是否满足收敛条件式（32）：若满足，则迭代结束；否则，将步骤4 中更新得到的响应变量组向下反馈至各子问题，同时根据式（31）更新拉格朗日乘子向量组，并令h=h+1。

步骤6 重复步骤3 — 5，直到满足收敛条件。

3 算例分析

3.1 算例参数

选取基于IEEE 118 节点系统的算例验证多场景SCUC 解耦机制的有效性。整个SCUC 模型包括96 个时段，每个时段为15 min。火电机组参数如附录C 表C1 所示。本文的研究重点在于计及风电不确定性的多场景多时段SCUC 问题的解耦求解方法，因此，以风电机组出力模型表示整座风电场的出力。在节点7、11、13、16、21处各增加1台风电机组，风力资源的相关数据参考文献［17］。利用蒙特卡罗抽样方法［18］生成20 个随机场景，各场景出现的概率均为1/20。风电机组预测出力如附录C 图C1 所示。负荷预测曲线如附录C 图C2 所示。为了确保SCUC模型结果的有效性，采用K-means聚类［18-21］的方式为基准场景生成数据。设置收敛精度ε=0.01，将拉格朗日乘子向量组的所有值均初始化为10，将惩罚因子设为1，将弃风成本系数设为200 元／MW。对于所有随机场景的SCUC模型以及基准场景的SCUC 模型，将总时段均划分为4 段。在MATLAB 2018b 中采用Yalmip 语言进行建模，并调用Gurobi 对模型进行求解。

3.2 确定性场景SCUC模型的解耦分析

为了验证本文所提多时段解耦机制的有效性，将确定性场景SCUC 模型结果作为并行求解方法的参考值。利用如式（36）所示指标e［22］衡量并行求解方法和传统集中式方法系统总成本的相对差别。

式中：Cd为并行求解方法的系统总成本；Cc为传统集中式方法的系统总成本。

表1为不同方法的结果对比，图4为并行求解方法的系统总成本曲线。2 种方法的成本存在一定的差异，这是由于传统集中式方法在求解时会在整个时段内寻找全局最优解，而并行求解方法会在各子问题对应的子时段内寻找局部最优解。传统集中式方法的求解时间为142.3 s，而并行求解方法总共迭代11 次，求解时间为70.2 s，比传统集中式方法的求解时间缩短了50.67 %。当时段数为2 时，并行求解方法的求解时间为91.2 s，当时段数为3 时，并行求解方法的求解时间为77.9 s，随着时段数的增加，求解时间逐步缩短。时段数越多，待求解的子问题模型数量也会随之增加，这会导致电脑的中央处理器和内存利用率过高，因此，当时段数达到一定数值后求解时间并不会明显缩短。由于不同电力系统的运行特性和不同计算设备的运行能力存在差异，如何选取最佳的时段数仍是一个有较大难度的问题。

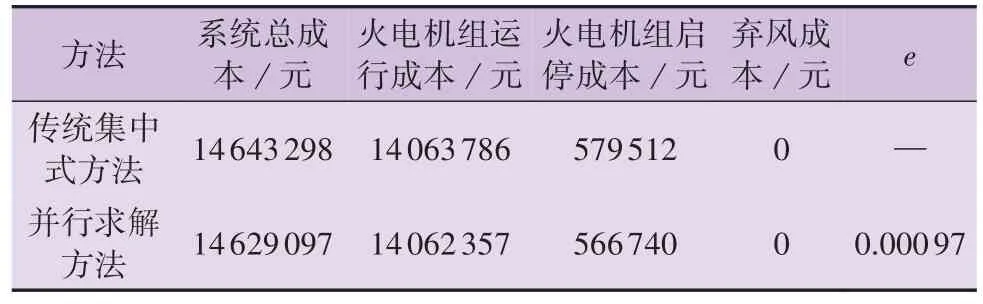
表1 不同方法的结果对比Table 1 Results comparison between different methods

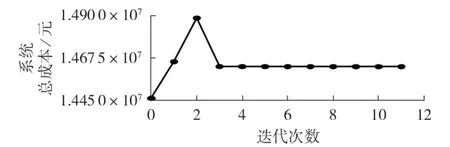
图4 并行求解方法的系统总成本曲线Fig.4 Total system cost curve of parallel solution method

图5 为不同方法的风电机组出力曲线。由图可知，2 种方法的风电出力曲线相似，这表明了多时段解耦机制的有效性。

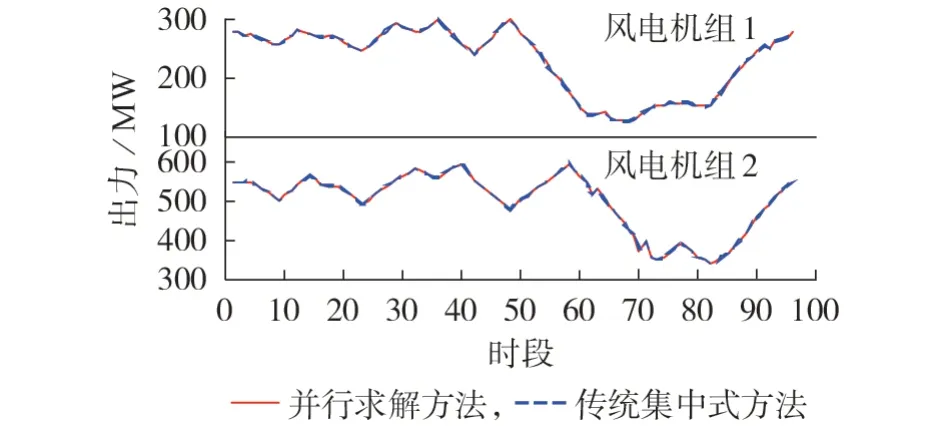
图5 不同方法的风电机组出力曲线Fig.5 Wind turbine output curves of different methods

表2 为部分火电机组在耦合时段的出力，子时段1与子时段2的耦合时段为25，子时段2与子时段3 的耦合时段为49。由表可知，这些火电机组在耦合时段的出力相同，这说明2 个连续子时段之间的共享变量差异接近于0。

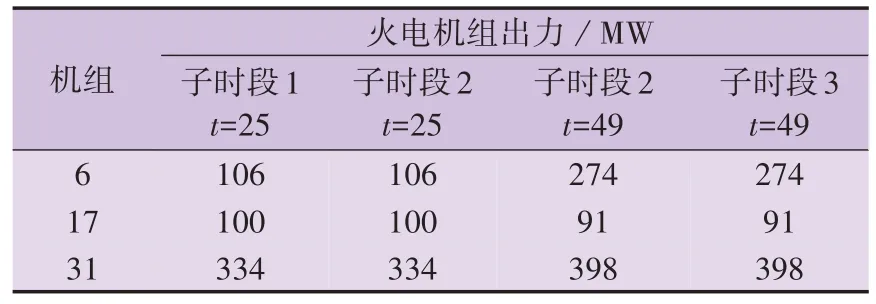
表2 部分火电机组在耦合时段的出力Table 2 Output of partial thermal power units in coupling periods

3.3 多场景SCUC模型的解耦分析

本节测试具有不同场景数的算例，设置时段数均为4，求解时间上限为5 h，若求解时间超过5 h，则默认不可解。

表3 为不同方法的求解时间。由表可知：随着场景数的增加，传统集中式方法的求解时间增长，当场景数增加到20 时，传统集中式方法不可解；相较于传统集中式方法，并行求解方法的求解时间较短，随着场景数的增加，电脑的中央处理器和内存利用率增加，并行求解方法的求解时间略有增长。

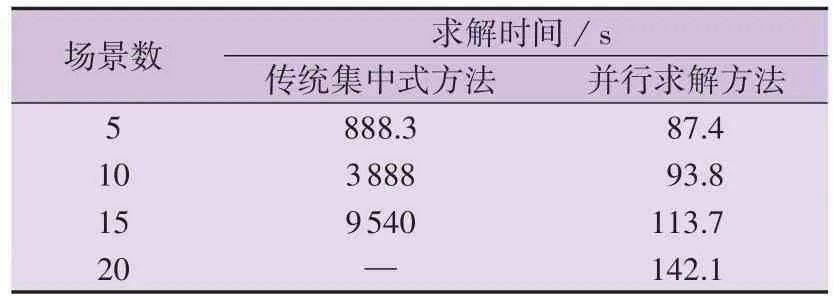
表3 不同方法的求解时间Table 3 Solution time of different methods

图6 为随机场景1 和基准场景下部分火电机组的出力曲线。由图可知，随机场景1 下的火电机组出力始终在出力上下限范围内，这表明了所提方法的有效性。

图6 随机场景1和基准场景下的部分火电机组出力曲线Fig.6 Output curves of partial thermal power units under Stochastic Scenario 1 and basic scenario

4 结论

本文提出一种基于ATC 算法的多场景多时段SCUC 问题解耦求解方法，采用2 种策略来降低SCUC 问题的复杂性并缩短求解时间。第1 种策略是采用一种多场景解耦机制，由于随机场景和基准场景之间存在火电机组爬坡的耦合，通过在子问题目标函数中添加惩罚项以及在子问题模型中添加一致性约束保证子问题解的可行性，将原始的多场景多时段SCUC 问题解耦为可以并行计算的单场景SCUC 问题。第2 种策略是采用一种多时段解耦机制，在多场景解耦的基础上，为了进一步缩短求解时间，将各单场景SCUC 问题根据时段划分为不同的子问题。算例结果表明，这些策略可以有效地缩短计及风电不确定性的多场景SCUC 问题的求解时间。后续笔者将进一步考虑多种新能源机组接入电力系统所带来的不确定因素，并研究相应的SCUC问题的分布式求解方法。

附录见本刊网络版（http：//www.epae.cn）。