构网型直驱风电机组间控制相互作用研究

王玉坤，张慕婕，李 壮，穆 清，王东泽，孙海顺，潘晓杰，邵德军

（1.国家电网公司华中分部，湖北 武汉 430070；2.中国电力科学研究院有限公司，北京 100192；3.华中科技大学 电气与电子工程学院 电力安全与高效湖北省重点实验室，湖北 武汉 430074）

0 引言

现有的风电机组变流器都是采用基于电网电压锁相的电流矢量解耦控制，以端电压相位为参考，控制注入电网的有功和无功电流，达到功率控制的目的。由于需要通过锁相控制对电网电压定向，又称该方法为跟网型控制。当风电场并网点所连交流系统较弱时，存在锁相、直流电压或电流控制不稳定导致的低频和次超同步振荡问题［1-3］。

构网型控制技术基于功率控制指令或者交流电压指令，通过虚拟同步控制等方法，生成变流器输出电压相位和幅值参考值。构网型控制无须通过锁相对电网电压定向，表现为受控电压源特性，具有较强的弱电网适应性。对于大规模风电接入弱交流电网的场景，将风电场部分风电机组设计改造为同时具有跟网型和构网型2 种控制模式，根据电网运行方式变化切换控制模式，构成混合机组风电场，可以消除风电场并网系统次超同步振荡风险［4-6］。

目前的构网型控制方法包括下垂控制［7-8］、虚拟同步控制［9-11］、惯性同步控制［12-14］、虚拟振荡器控制［15］等，其中虚拟同步控制模拟同步发电机的转子运动惯量和阻尼特性，是目前主流的构网型控制策略之一，已经应用于构网型双馈和直驱风电机组样机的研发和试验中［15-17］。

研究表明，构网型风电机组的控制会参与跟网型风电机组并网的次超同步振荡模式并对其产生较强的阻尼作用，风电场投入少量构网型风电机组可以有效抑制次超同步振荡［18］。但是构网型风电机组采用模拟同步发电机转子运动的虚拟同步控制模式，会引入对应的低频特征模式，跟网型风电机组对该模式无影响。当混合风电场内投入的构网型风电机组容量太小时，构网型风电机组对应的等效短路比很高，低频特征模式会出现振荡失稳［18-19］。为此文献［18］研究了混合风电场构网型控制风电机组的容量配比问题，并提出了容量配比原则。

风电场内多台构网型风电机组并联运行时，虚拟同步控制会引入机组间相互作用的低频振荡模式，其稳定性是混合风电场运行需要关注另一个重要问题，目前尚无相关研究报道。本文采用特征模式分析方法，研究了基于虚拟惯量控制方法的构网型直驱风电机组并联运行时的控制相互作用及主导低频失稳模式稳定性，揭示了虚拟惯量控制参数及系统运行方式对构网型风电机组并列运行低频振荡特性的影响，并通过详细时域仿真验证了分析结果的正确性，相关研究结论可用于指导构网型风电机组控制技术的工程应用。

1 基于虚拟同步控制的构网型直驱风电机组数学模型

构网型直驱风电机组与现有跟网型直驱风电机组的主要区别在于变流器控制不同，其结构如图1所示。图中：Udc、Udcref分别为直流电容Cdc两端电压及其参考值；usd、usq和usdref、usqref分别为机侧输出电压us的d、q轴分量及其参考值；isd、isq和isdref、isqref分别为机侧输出电流is的d、q轴分量及其参考值；usdm、usqm和isdm、isqm分别为机侧输出电压和电流经滤波后的d、q轴分量；ωm为发电机转子角速度；Ps为发电机输出的有功功率；Pref、Qref分别为有功、无功功率参考值；Pg、Qg分别为网侧有功、无功功率；ω0为电网额定角频率；U0、Uref分别为风电机组机端电压幅值的额定值及其参考值；Lg为网侧滤波电感；θs为直驱风电机组输出的相位角；θv为虚拟同步控制生成的电压相位角；igdm、igqm分别为网侧输出电流ig经滤波后的d、q轴分量；ugdm、ugqm分别为风电机组机端电压ug经滤波后的d、q轴分量；igd、igq和ugd、ugq分别为网侧输出电流和风电机组机端电压的d、q轴分量；ugcdref、ugcqref分别为网侧端口电压的d、q轴参考值；Tm为一阶滤波器的时间常数。

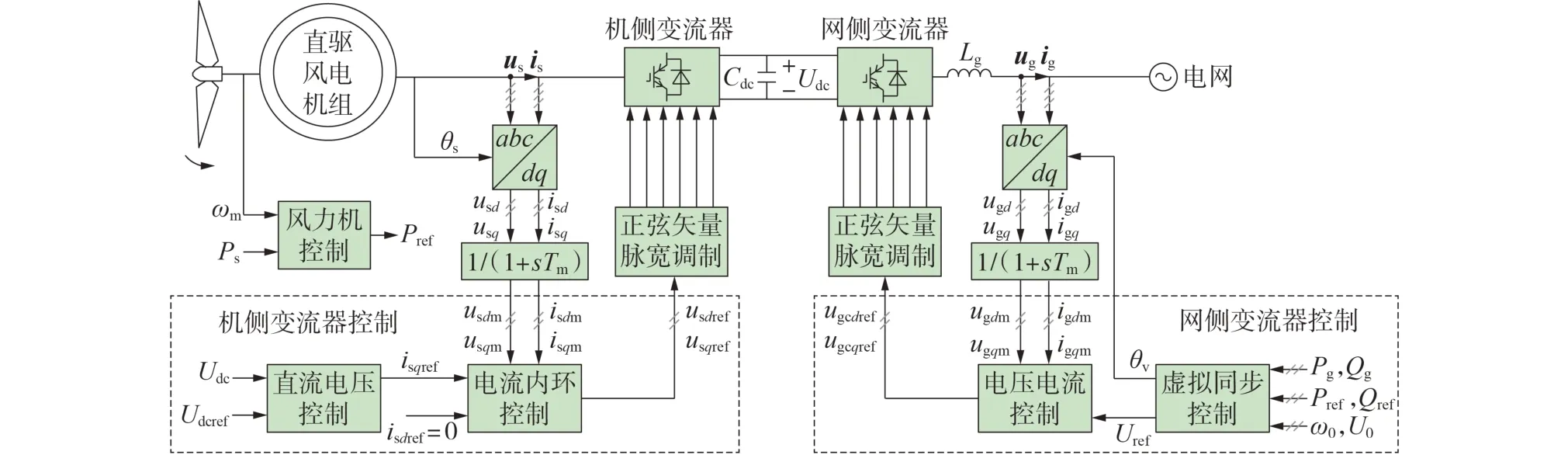
图1 构网型直驱风电机组并网系统及其控制结构Fig.1 Grid forming direct-drive wind turbine grid-connected system and its control structure

构网型直驱风电机组机侧变流器控制直流电压的稳定；网侧变流器采用虚拟同步控制，在控制风电机组并网有功和无功功率的同时，模拟同步机特性，使得风电机组能够主动响应电网频率变化和提供无功电压支撑。

1.1 机侧变流器控制数学模型

构网型直驱风电机组的机侧变流器包括外环直流电压控制和内环电流控制双闭环控制回路，外环直流电压控制维持背靠背变流器的直流电压稳定，内环电流控制采用永磁电机转子磁链定向矢量控制，保持机侧输出电流d轴分量isd为0，控制框图如图2 所示。图中：Ψf为转子磁链；Lsd、Lsq分别为发电机定子d、q轴电感；Kp1、Ki1分别为外环直流电压控制比例、积分参数；Kp3、Ki3和Kp2、Ki2分别为机侧d轴和q轴内环电流控制的比例、积分参数。

引入中间变量z1—z3，列写机侧变流器控制部分状态空间方程如式（1）所示。

1.2 网侧变流器控制数学模型

网侧变流器控制由虚拟同步控制以及外环电压、内环电流控制组成，控制框图如图3 所示。图中：Pf为虚拟调速器附加的功率参考值；nq为无功下垂系数；ωg、ωgb分别为电网侧同步角速度及其基准值；Rv、Lv分别为虚拟电阻、电感系数；J、D分别为虚拟惯量、阻尼系数；Kp4、Ki4和Kp6、Ki6分别为网侧d、q轴外环电压控制比例、积分参数；Kp5、Ki5和Kp7、Ki7分别为网侧d轴和q轴内环电流控制比例、积分参数；Kw为有功调频系数。

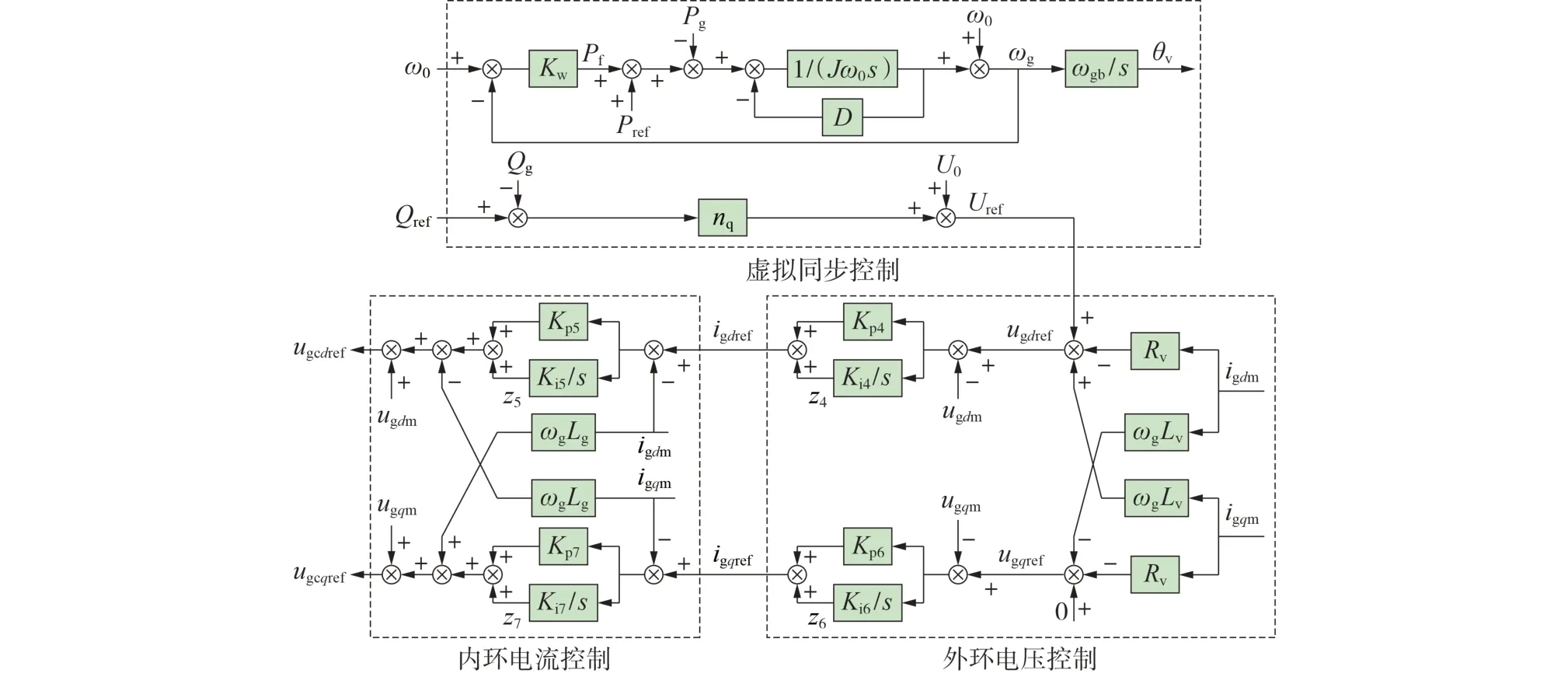
图3 构网型直驱风电机组网侧变流器控制模型Fig.3 Grid side converter control model of grid forming direct-drive wind turbine

由图3 可知：虚拟惯量的虚拟同步控制包括有功相位控制和无功电压控制2 条通道。有功相位控制根据风电机组最大功率点跟踪控制产生的有功功率参考值Pref和实际网侧有功功率Pg，模拟转子运动产生变流器输出电压相位指令，输出电压相位指令过程相当于跟网型控制中的锁相输出环节，用于电流矢量解耦控制，其方程如式（2）所示。

无功电压控制通道根据无功功率参考值和实际网侧无功功率产生风电机组机侧变流器输出电压幅值指令，此处采用调差控制，其方程式见式（3）。

外环电压控制以输出电压相位为坐标参考，控制q轴电压为0，d轴电压为电压幅值指令，输出相应的d、q轴电流指令。外环电压控制也可引入虚拟阻抗（如图3中Rv+jωgLv所示），等效于控制机端经过虚拟阻抗后的电压幅值和相位为虚拟同步控制产生的指令。内环电流采用矢量解耦控制。引入中间变量z4—z7后，网侧电压电流控制方程为：

1.3 构网型直驱风电机组状态空间模型

考虑直驱风电机组转子运动方程、永磁电机动态方程、变流器直流电容动态、输出滤波以及脉宽调制控制动态［6］等，联合式（1）—（4）所示变流器控制方程，可以构建构网型直驱风电机组的状态空间方程及其线性化模型，如式（5）所示。

式中：ugGFM=［ugd，ugq］T为机端电压向量；igGFM=［igd，igq］T为机端电流向量；ΔXGFM为构网型直驱风电机组对应的全部状态变量，共27 维，即ΔXGFM=［Δωm，Δωref，Δx1，Δisd，Δisq，Δisdm，Δisqm，Δz1，Δz2，Δz3，Δusd，Δusq，ΔUdc，Δigd，Δigq，Δigdm，Δigqm，Δugdm，Δugqm，Δz4，Δz5，Δz6，Δz7，Δugcd，Δugcq，Δωg，Δθvsg］T，Δx1为功率外环输出量的线性化状态量，变量前方的Δ 表示对应变量的小扰动量；AGFM、BGFM、CGFM、DGFM为系数矩阵。

2 两机并联运行小扰动稳定性分析

为了研究构网型直驱风电机组并联运行的主导特征模式及其稳定性，考虑2 台构网型直驱风电机组W1、W2并联运行。含构网型直驱风电机组的两机并联运行并网系统拓扑结构如图4 所示。图中：Lm为连接线路电感；并网点交流系统采用等值电势源E表示；Ls为内电感。

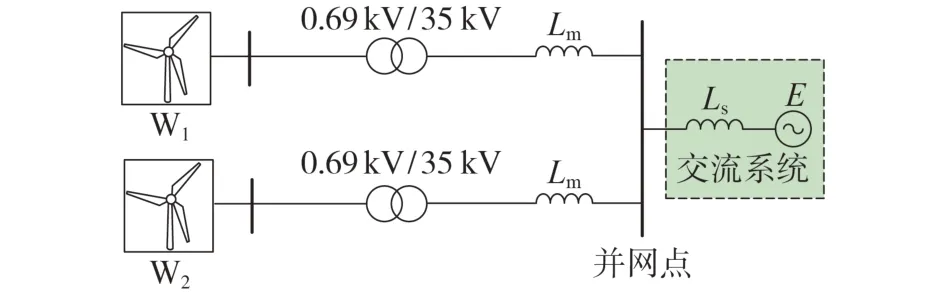
图4 含构网型直驱风电机组的两机并联运行并网系统拓扑结构Fig.4 Topology structure of double-machine parallel operation grid-connected system with grid forming direct-drive wind turbine

由式（5）所示构网型直驱风电机组的状态空间模型，联立机端升压变压器、并网线路及交流系统等值电势源的电压电流方程，消去式（5）中代数方程，可得式（6）所示算例系统线性化状态空间方程。

式中：ΔX为2 台构网型直驱风电机组对应的全部状态变量；A为线性化状态空间方程状态变量系数矩阵。

2.1 两机并联运行并网系统特征模式分析

设并网点的短路比SSCR=6，风电机组直接与并网点相连，即Lm=0，风电机组W1、W2的运行工况和参数相同，风电机组控制参数设置见附录A表A1，不考虑风电机组外环电压控制中的虚拟阻抗环节，计算两机并联运行并网系统特征值，部分特征模式见表1。

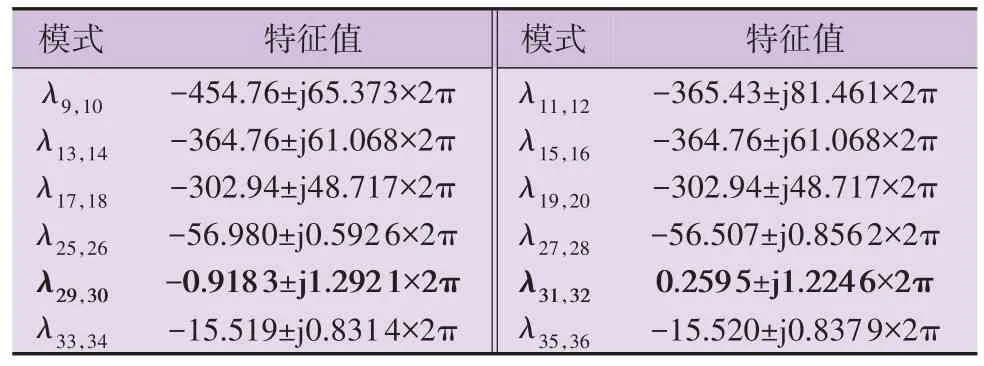
表1 含构网型直驱风电机组的两机并联运行并网系统低频特征模式Table 1 Low frequency characteristic modes of doublemachine parallel operation grid-connected system with grid forming direct-drive wind turbine

系统特征模式中，次超同步振荡模式均为稳定模式，说明构网型直驱风电机组控制不会引起次超同步振荡问题。系统存在2 对靠近虚轴的低频特征模式，如表1中λ29，30、λ31，32，且模式λ31，32处于不稳定状态。

对上述2对特征模式进行参与因子分析，结果见图5，可以发现2 对低频特征模式与2 台风电机组的虚拟同步控制及网侧变流器外环电压控制强相关。

图5 低频特征模式（λ29，30和λ31，32）的参与因子Fig.5 Participation factor of low frequency characteristic modes（λ29，30 and λ31，32）

在罗盘图中画出上述2 对低频特征模式的右特征向量中对应风电机组输出电流、直流电压及相位输出等状态变量，可以反映各状态变量中该模态分量的相位和幅值间相对关系，如图6 所示。可以看出：2 台构网型直驱风电机组输出电流中低频特征模式λ29，30分量同相位，表现为2 机共同相对交流系统的振荡，为共模模态；低频特征模式λ31，32分量反相，表现为2台机组之间的相互作用，为异模模态。

图6 低频特征模式（λ29，30和λ31，32）右特征向量罗盘图Fig.6 Compass graph of right eigen vector of low frequency characteristic modes（λ29，30 and λ31，32）

低频特征模式分析结果表明：2 台构网型直驱风电机组并联运行时，存在2 对由虚拟同步控制和网侧变流器外环电压控制主导的低频振荡模式，分别对应两机并联运行并网系统的共模模态和异模模态，其中异模模态不稳定说明2台构网型直驱风电机组之间存在由控制相互作用导致的振荡失稳问题。

2.2 时域仿真分析

建立两机并联运行并网系统的详细电磁暂态仿真模型，风电机组控制参数按照表1 特征值计算条件确定，初始条件下设Lm为0.1 p.u.，系统达到稳态后第10 s 将Lm变为0，风电机组输出功率以及注入交流系统功率仿真结果如图7所示。

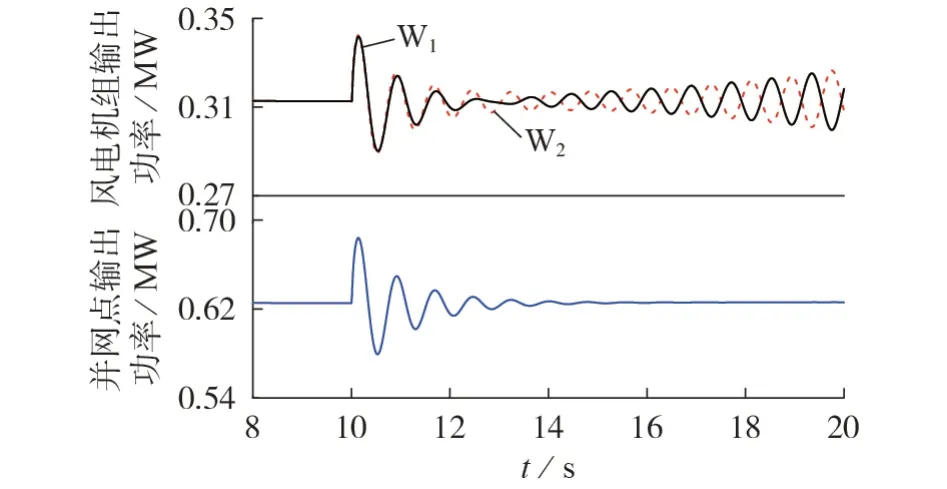
图7 含构网型直驱风电机组的两机并联运行并网系统扰动仿真Fig.7 Disturbance simulation of double-machine parallel operation grid-connected system with grid forming direct-drive wind turbine

由图7可见：2台风电机组输出功率首先呈现对电网的共模振荡，且该模态的振荡幅值逐渐衰减至0，同时2 台风电机组共同注入交流系统的振荡功率也衰减到0，随后2台风电机组输出功率呈现异模振荡并发散，与表1所示特征值分析结果一致。

3 机组间相互作用的关键影响因素分析

由参与因子分析结果可知，2 台构网型直驱风电机组并联运行的共模模态和异模模态由虚拟同步控制、网侧外环电压控制主导，分别反映2 台构网型直驱风电机组与交流系统间以及风电机组间相互作用，以下分别从并网电气距离（短路比、两机并网线路长度）、关键控制参数等方面对影响机组间相互作用稳定性的关键因素进行分析。

3.1 并网电气距离的影响

3.1.1 特征根轨迹分析

以表1 计算条件为基准，分别改变两机并联运行并网系统的短路比（SSCR：5 → 7）和两机并网线路长度（Lm：0 → 0.05 p.u.），计算共模模态和异模模态根轨迹，如图8 所示。由图可见：增大并网点短路比，共模模态阻尼减弱，异模模态基本不受影响，这说明交流电网强弱主要影响并网运行机组的共模模态稳定性，对异模模态稳定性几乎无影响；增加两机并网线路长度，共模和异模模态阻尼均增大，说明构网型直驱风电机组间相互作用的异模模态稳定性与两机并网线路长度密切相关，两机并网线路长度为0 时异模模态不稳定，随着两机并网线路长度增加，异模模态逐渐趋于稳定。

3.1.2 时域仿真

基于图7 仿真工况，分别修改短路比和机组并网线路长度（第10 sLm发生变化），仿真结果见图9。对比图9与图7仿真结果可以发现：短路比减小时共模模态振荡衰减相对较快，异模模态振荡基本无变化；而增加机组并网电气距离，异模模态振荡稳定。时域仿真结果验证了根轨迹分析结果的正确性。

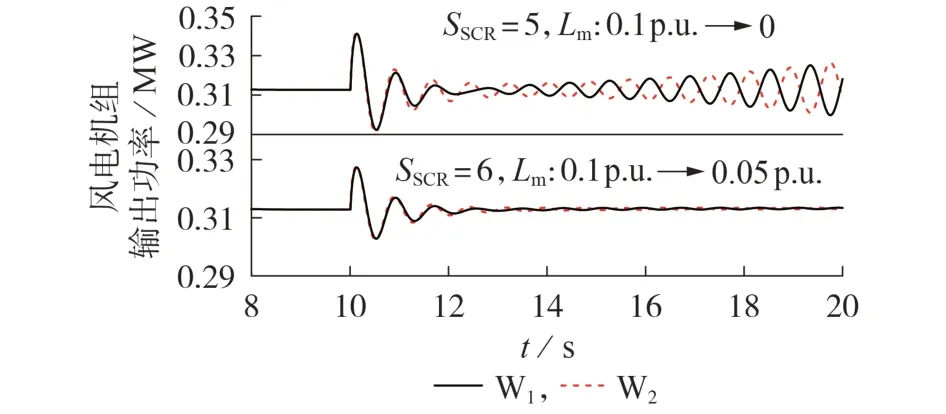
图9 并网电气距离对机组间相互作用的影响Fig.9 Impact of electrical distance on interaction between grid forming direct-drive wind turbines

3.2 虚拟同步控制参数的影响

本文虚拟同步控制采用的虚拟转子运动方程根据有功指令控制风电机组出口电压相角，虚拟惯量系数J和虚拟阻尼系数D是其重要参数。

3.2.1 特征根轨迹分析

仍然基于表1 所示计算条件，分别设置如下工况：①虚拟惯量系数J由0.2 p.u.增加到1 p.u.；②虚拟阻尼系数D由30 p.u.增加到50 p.u.，保持系统其余参数不变，计算两机并联运行并网系统共模和异模模态的根轨迹，如图10所示。

根轨迹结果表明：虚拟惯量系数J的增大会导致异模模态呈现负阻尼特性，共模模态阻尼也会降低；虚拟阻尼系数对共模和异模模态频率有明显影响，对2 种模式的阻尼有一定程度的改善，但是在所设参数范围内对异模模态稳定性的改善作用不足以令其达到稳定状态。

3.2.2 时域仿真

仍然基于图7 的仿真工况，分别设置：①虚拟惯量系数J为0.3、0.7、1 p.u.；②虚拟阻尼系数D为30、40、50 p.u.。在t=10 s 时，将Lm由0.1 p.u.变为0，仿真结果如图11 所示。可以看到：当J=0.3 时异模模态进入稳定状态，即虚拟阻尼系数对异模模态阻尼有一定影响；共模模态始终保持稳定。这与根轨迹分析结果一致。

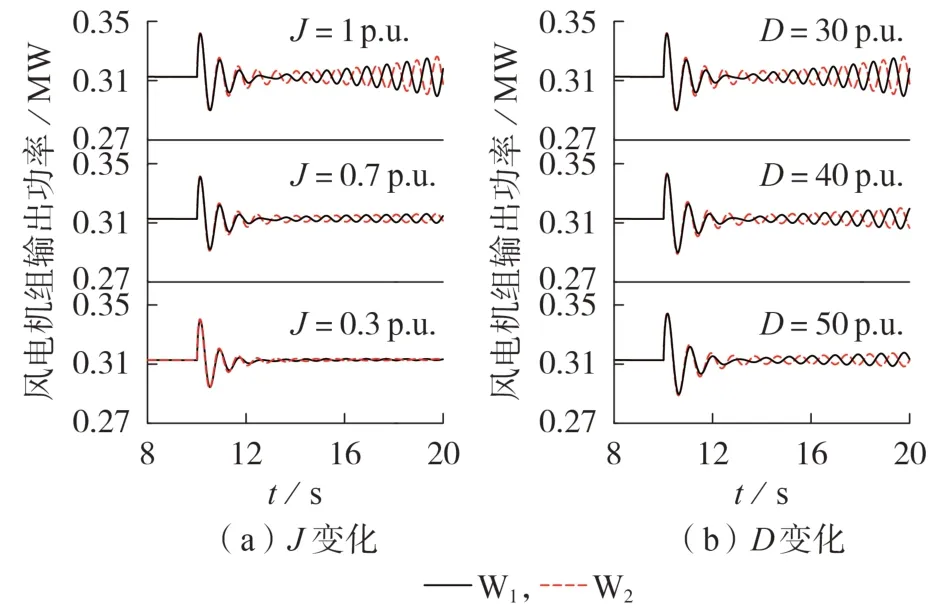
图11 不同虚拟同步控制系数变化下的系统扰动仿真Fig.11 Disturbance simulation when different virtual synchronous control parameters change

虚拟同步控制模式下，虚拟惯量系数和虚拟阻尼系数是影响构网型直驱风电机组响应系统功率不平衡（惯量和一次调频）能力的重要参数，本文分析结果表明，虚拟同步控制参数设计还需要考虑机组并网振荡稳定性约束。

3.3 网侧外环电压控制参数的影响

构网型直驱风电机组网侧变流器外环电压控制以虚拟转子运动方程输出的电压相位指令为dq坐标参考，采用比例积分控制令q轴电压为0，d轴电压为无功控制输出的幅值参考值；另一方面，外环电压控制还可以引入虚拟阻抗Rv+jωLv，构网型控制等效为具有内阻抗的受控电压源。以下研究外环电压控制其比例系数对异模模态稳定性的影响。

3.3.1 特征根轨迹分析

基于表1 计算条件，设置如下工况：①改变网侧外环电压控制的比例系数（Kp4：1.2 p.u.→1.34 p.u.）；②改变虚拟电阻系数（Rv：0 → 0.1 p.u.，Lv=0）；③改变虚拟电感系数（Rv=0，Lv：0.3 p.u.→ 0.37 p.u.）。计算两机并联运行并网系统共模和异模模态的根轨迹如图12所示。

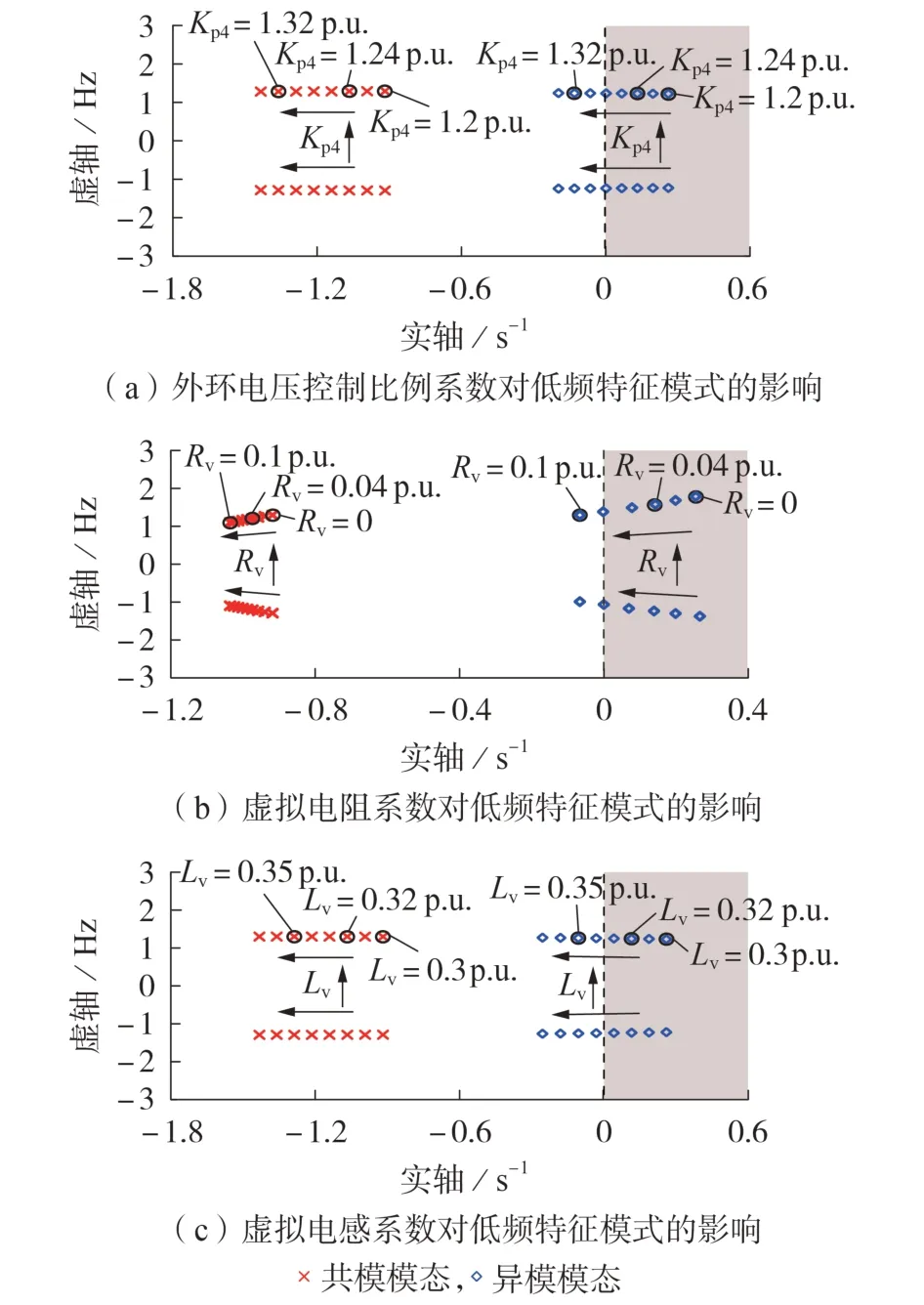
图12 外环电压控制参数对低频特征模式的影响Fig.12 Impact of outer-loop voltage control parameters on low frequency characteristic mode

根轨迹结果说明，随着网侧外环电压控制比例系数增大，异模模态逐渐从负阻尼状态趋于稳定的正阻尼状态，共模模态阻尼也得到增强。采用虚拟电阻或虚拟电感控制，均可有利于提高共模和异模模态稳定性。

3.3.2 时域仿真

基于图7 的仿真工况，分别设置如下工况：①网侧外环电压比例系数Kp4分别为1.2 p.u.和1.32 p.u.；②虚拟电阻系数为0 和0.1 p.u.；③虚拟电感系数Lv为0.3 p.u.和0.35 p.u.。在t=10 s 时，将Lm由0.1 p.u.变为0，两机系统功率振荡曲线见图13。仿真结果验证了根轨迹分析结果。

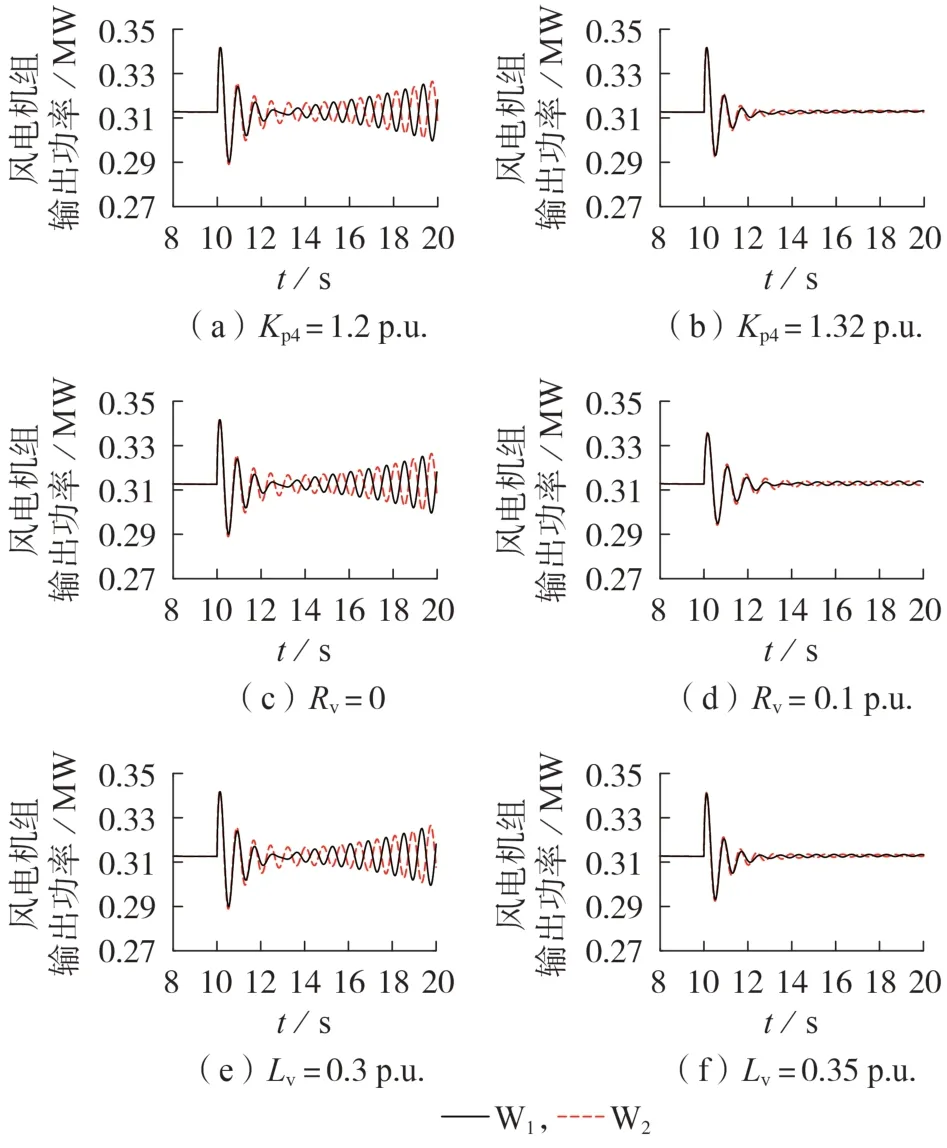
图13 不同外环电压控制参数的功率振荡曲线Fig.13 Power oscillation curves with different outer-loop voltage control parameters

以上分析表明，构网型直驱风电机组网侧外环电压控制比例系数对异模模态稳定性有重要影响，引入虚拟阻抗控制可以有效稳定异模模态振荡模式。从机理上理解，构网型控制等效为理想受控电压源，引入虚拟阻抗控制后机组等效为具有内阻抗的受控电压源。电路中2 个理想电压源难以并联运行，而具有内阻抗的电势源并联更容易实现稳定运行。

4 多机并联运行的控制相互作用分析

分别考虑1 — 4 台同型构网型直驱风电机组直接并联运行，设置并网点短路比为6.0，计算系统特征模式，结果如表2所示。

表2 多台构网型直驱风电机组并联运行并网系统低频特征模式Table 2 Low frequency characteristic modes of grid-connected system with parallel operation of multi grid forming direct-drive wind turbines

多台同型构网型直驱风电机组以相同电气距离并联运行时，分析结果可得如下结论：①共模模态稳定性与单台等值机组并网系统一致；②异模模态的数量与风电机组数量有关，控制参数和电气距离一样的情况下，所有异模模态的稳定性与两机并联运行并网系统的异模模态一致。

实际风电场是多台风电机组通过交流汇集组成，多台构网型控制机组间的相互作用须根据风电场结构构建算例进行分析。相比两机并联分析的结果，实际风电场多机联合运行的情况，机组间控制相互作用的低频模式稳定性趋势应该具有相似性。

5 结论

本文基于两机并联运行并网系统，研究了采用虚拟同步控制的构网型直驱风电机组之间的控制相互作用模式及其稳定性，主要研究结论如下：

1）构网型直驱风电机组并联运行时，存在一对共模模态和一对异模模态，异模模态反映机组之间的控制相互作用，共模模态反映两机并联运行系统与电网间的相互作用；2 种模态均为与机组虚拟同步控制和网侧外环电压控制强相关的低频控制模式；

2）并联运行机组间的电气距离对异模模态稳定性具有重要影响，并联运行的构网型直驱风电机组存在控制相互作用引起的低频异模模态振荡风险；

3）虚拟惯量系数对共模和异模模态稳定性具有重要影响，虚拟阻尼系数对振荡模式频率有明显影响，需要与机组等效惯量和一次调频能力协调设计；

4）网侧外环电压引入虚拟阻抗控制等效为增加机组间电气距离，有利于异模模态的稳定性，是解决机组间控制相互作用的有效方法。

结合风电场实例，研究同时具有构网型和跟网型机组甚至全构网型机组的风电场并网稳定性是未来需要进一步开展的研究工作。此外，将构网型控制技术应用到静止无功补偿、储能、柔性直流换流器等大容量并网变流器是未来新型电力系统关键支撑技术的重要研究方向，本文研究工作也是开展相关研究的基础。

附录见本刊网络版（http：//www.epae.cn）。