传统交流线路保护在换流器并网系统中的适应性分析
2024-03-26宋国兵侯俊杰李唯嘉张晨浩
常 鹏,宋国兵,侯俊杰,李唯嘉,张晨浩
(1.西安交通大学 电气工程学院,陕西 西安 710049;2.新疆大学 电气工程学院,新疆 乌鲁木齐 830046)
0 引言
伴随着“双碳”战略的执行及电力电子技术的高速发展,我国电网中电力电子设备的渗透率日益提升[1],截至2022年底,我国可再生能源装机容量已达到1.213 × 109kW,占全国发电总装机容量的47.3 %。然而,大规模电力电子设备的接入为我国能源转型带来机遇的同时,也为电网引入了迥异于传统电网的故障特征,这使得过去依赖传统电网故障特征的保护原理在电力电子设备接入系统中存在适应性问题。为了保障电力系统的安全运行,有必要对传统保护在电力电子设备接入系统中的适应性进行研究。
针对纵联差动保护的适应性,文献[2]首先分析了故障分量电流差动保护的最佳适用条件,然后通过仿真探索了风机的故障特征,最后通过比较保护最佳适用条件和系统故障特征的匹配程度对保护适应性进行了评估;文献[3]推导了逆变器短路电流的解析表达式,指出了电流差动保护在逆变器并入弱电网时存在拒动风险;文献[4]综合考虑了故障类型、电压不平衡度、功率参考值等因素的影响,对电流相位差动保护在柔性直流系统的适应性进行了评估。针对保护辅助元件的适应性,文献[5-6]研究了选相元件及方向元件在风电系统中的适应性,其结论简洁明了,但分析过程过于依赖仿真,缺乏对风机故障特征的理论推导;文献[7]对换流器的序阻抗特征进行了理论推导,然后结合保护判据对突变量方向元件的适应性进行了评估;文献[8]基于柔性直流换流器的控制策略研究了负序方向元件在系统中的适应性,并提出了改进方案;文献[9]和文献[10]分别研究了电流序分量选相元件和电流突变量选相元件在换流器并网系统中的适应性,并提出了性能优化方案。针对距离保护的适应性,文献[11]对工频量距离保护和时域距离保护在风电系统的适应性进行了分析,指出换流器的频率偏移特性对工频量距离保护存在影响,但研究过程中忽略了过渡电阻的影响;文献[12]研究了比相式距离保护在风电系统中的适应性,指出了风电序阻抗的不确定性将造成保护范围时变,从而恶化保护性能;文献[13]研究了正序电压极化距离保护在柔性直流系统中的适应性,分析了控制策略对保护的影响。
综上所述,已有研究针对保护适应性问题得到了大量有价值的结论,但也可以看到这些研究大多趋向于定性分析,缺乏对不同故障场景下故障特征的详细推导,难以给出保护适应性的定量边界,且其中鲜有文献综合考虑系统参数和换流器控制策略对保护的影响,因此所得结论具有一定的局限性。为了改进上述缺陷,本文首先提出了一种具有普适性的保护适应性评估方法;然后,针对新型电力系统典型拓扑,对换流站在不同场景下的电气量特征进行定量分析;其次,结合提出的保护适应性评估方法和研究得到的换流站电气量特征,对传统交流线路保护在换流器并网系统中的适应性进行了评估,并推导了保护适应边界,针对部分存在适应性问题的保护,提出了优化方案;最后利用PSCAD 仿真对保护适应性分析的正确性和优化方案的有效性进行验证。
1 适应性评估方法
本章从继电保护的本质出发,研究保护适应性的评估方法:所有保护的背后都有一个最佳适用模型,保护判据的构建依赖最佳适用模型的故障特征,当实际检测到的故障特征匹配最佳适用模型的故障特征时,保护总是适应的。因此,可以通过比较检测得到的故障特征和保护最佳适用模型故障特征的匹配度实现保护适应性评估。
值得指出的是,与基于电力元件等效模型推导得到的故障特征不同,实际系统中检测到的故障特征受电力元件实际模型与等效模型匹配度、互感器精度等因素的影响。因此,在推导实际检测到的故障特征时,上述因素应被综合考虑。
综上所述,本文提出了图1 所示的适应性评估方法,具体步骤如下:①基于保护原理,研究保护最佳适用模型,并利用模型的源/参数特性实现保护最佳适用模型对应故障特征的数学描述(因为故障特征取决于系统的源/参数特性);②针对被保护元件,综合考虑等效模型和实际模型的差异、互感器精度等因素的影响,利用源/参数特性实现被保护元件故障特征的数学描述;③当被保护元件故障特征的数学描述匹配保护最佳适用模型对应的数学描述时,保护适应,否则保护不适应。
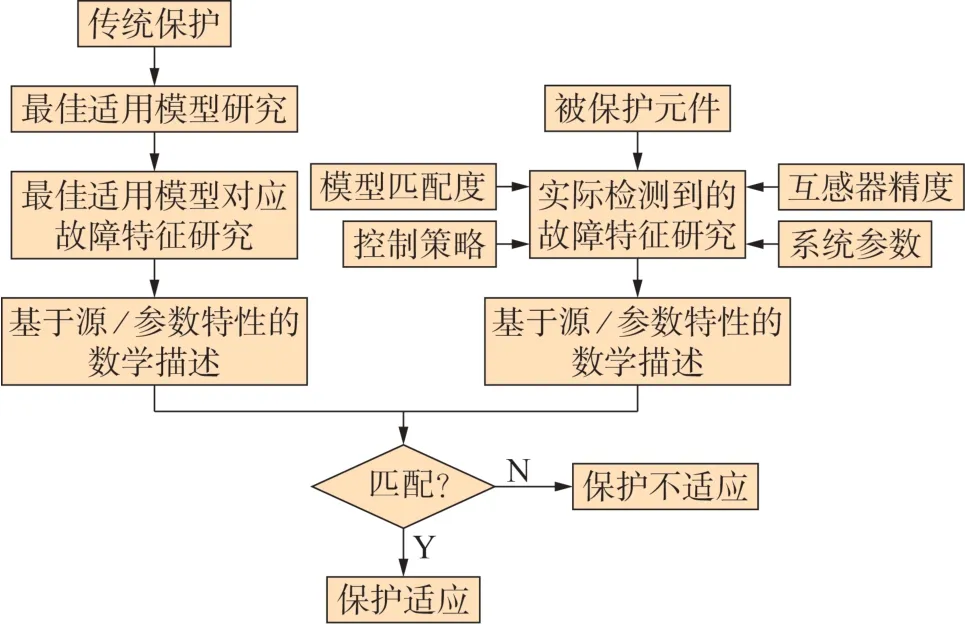
图1 基于最佳适用模型匹配度的保护适应性评估方法Fig.1 Protection adaptability evaluation method based on matching degree of best applicable model
当系统含换流站时,换流站的源/参数特性与故障场景、控制策略等多种因素有关,为波动量,基于图1 所示的保护适应性评估方法,可以通过探索该波动量是否满足保护最佳适用模型对应的源/参数特性实现保护适应性评估。
特别地,对于母线侧并入换流器和多条交流馈线的交直流多馈入系统而言,当某一馈线发生故障时母线背侧系统等效参数为换流站参数(波动量)和非故障馈线参数(恒定量)的结合,为此本文进一步提出了针对该场景的保护适应性定量评估方法,如附录A图A1所示。该场景下可以首先固定波动量,随后推导保护性能满足要求时对应的恒定量约束条件,并将该约束条件作为保护适应性评估的定量指标。在此记约束条件的通用表达式为F(x1,x2,…),其中xi(i=1,2,…)表示不同的参数变量,例如背侧阻抗、电压等级、容量等。而针对不同的保护原理,约束表达式可以是单个参数变量的线性组合或多个参数变量的非线性组合。
2 典型场景及特性分析
2.1 典型场景分析
换流器并网系统典型场景可以分为集中式新能源汇集系统、100 % 新能源电网、特高压直流系统、柔性直流系统4 类。本文选取由电压源型换流器(voltage source converter,VSC)组成的集中式新能源汇集系统以及由模块化多电平换流器(modular multilevel converter,MMC)组成的柔性直流系统作为研究对象,图2(a)—(c)分别展示了VSC 和MMC的单馈入受端拓扑以及VSC的多馈入受端拓扑。图中:Um和Im分别为m侧电压和电流;Uf和If分别为故障点f的电压和电流;In为n侧电流;Rf为过渡电阻;Zn和En分别为常规系统的阻抗和电动势,本文设定En的相位为0°;Zfm和Zfn分别为点f至m侧和n侧的阻抗;Zζ和u分别为非故障馈线的阻抗和电动势。
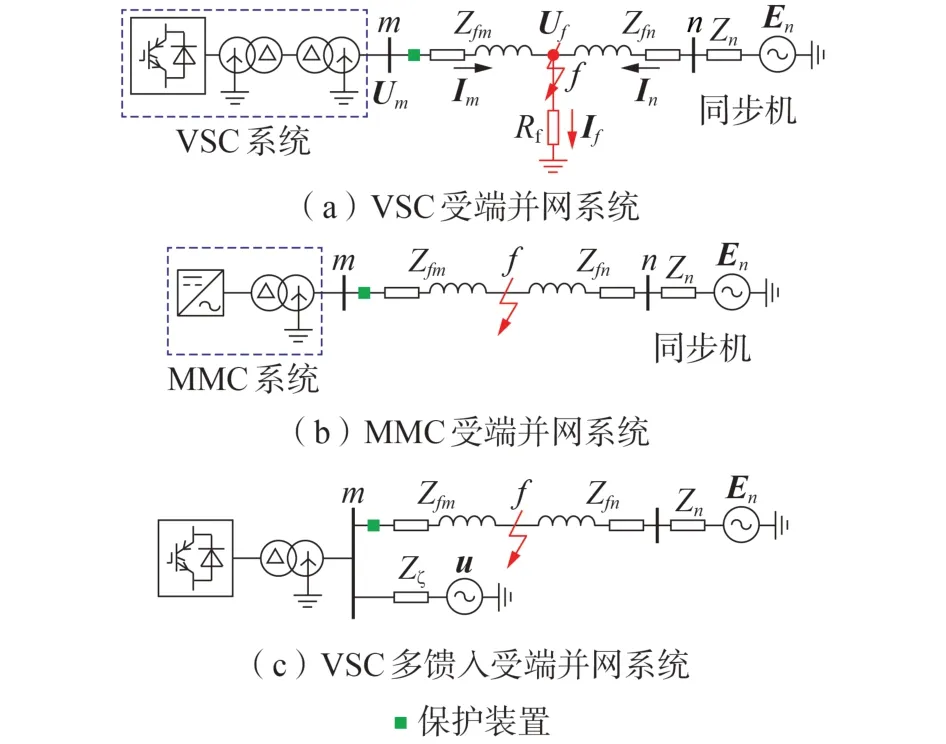
图2 新型电力系统典型拓扑Fig.2 Typical topology of new power system
2.2 换流站特性分析
本节对换流站侧故障前、后的电气量特性和等值阻抗进行研究,其中换流站侧等值阻抗Zm定义为:
式中:Δ表示突变量,后同。
2.2.1 正常运行状态下的换流站特性
基于变压器变比将图2(a)转化为图3。图中:US为经等效变换后的换流站控制点S的电压(本文假定控制点在变压器前);ZT为控制点至保护安装处的等效阻抗(变压器和并网联络线阻抗之和)。

图3 换流器并网系统等效拓扑Fig.3 Equivalent topology of inverter-interfaced system
依据现有的控制策略,系统正常状态下控制点电压U[0]S和I[0]m同相位(上标“[0]”表示正常运行时的电气量,后同)。基于图3和argZT≈ 90°的假设,可以推导得到U[0]S、I[0]m和U[0]m在空间的分布如图4所示,在此记I[0]m超前U[0]m的相位为δ,其取值和ZT有关,当变压器的等值短路阻抗取15 % 时,δ≈arcsin 0.15 ≈ 8.63°。

图4 系统正常运行时的电气相量图Fig.4 Phasor diagram of electrical quantities during normal operation of system
2.2.2 交流故障下的换流站特性
依据实际工程资料和调研[14-15],交流故障下部分MMC 系统的控制指令如式(2)所示,本文记为不注入无功策略;VSC 不对称故障、三相故障下的部分控制指令分别如式(3)、(4)所示,本文中记为注入无功策略。
式中:id1ref和iq1ref分别为正序电流在d、q轴下的参考值;Pref为输出功率;IN为额定电流;Imax为换流器最大耐受电流,其一般为1.2IN~2IN;U1为控制点正序电压的幅值,U*1为其标幺值。
由于篇幅限制,本节后续只分析了换流器采用式(3)、(4)对应控制策略且系统发生三相故障和单相接地故障时的故障特征,其他类型故障的故障特征可参考这2种故障的分析过程。
1)三相故障。
当交流线路发生三相高阻故障时,Im超前Um的相位很小,此时换流器可以近似为一个幅值很大的负阻抗。依据图2(a),In可以表示为:
式(5)中,当Rf较大但小于Um/Im的实部时,Rf//(-Um/Im)往往幅值很大且位于第一象限,因此argIn往往小于0°。考虑到换流器的弱馈性,If由In主导,而Uf=IfRf,因此argIn和argUn均小于0°。由于常态下的沿线电压相位近似相等,因此故障后电网电压相位一般滞后于故障前,系统发生三相高阻故障时m侧电气量如附录A 图A2 所示,此时arg(-ΔUm/ΔIm) ∈ (0°,180°)。
当交流线路发生三相低阻故障时,In和Uf可以近似表示为:
式(6)中,假定arg(Zn+Zfn) = 85°,Rf很小时可推导得到argUf≈ -85°。根据式(4),US严重跌落时电流控制指令应满足电路拓扑,此时Im滞后US近90°,进一步可推导得到ImZT、ImZfm近似和US同相位,因此US、Um和Uf近似同相位,该场景下m侧电气量的空间分布如附录A 图A3 所示,可知arg(-ΔUm/ΔIm)可能大于180°。
下面进一步推导Zm在不同场景下的波动范围。本文中换流器作用于控制点,因此首先推导控制点背侧阻抗ZS,然后通过式(7)计算Zm。
在此定义故障后US的相位变化量为φu,幅值与故障前幅值之比为ku。为了更好地应对不同的故障场景,确保所有等值正序阻抗均被考虑在内,对不同电压跌落下φu的取值进行讨论:①当ku≥ 0.8 时,US可用Uf近似,基于式(6)可知当时有argUf≈-arctan 0.75≈ -37°,取一定的裕度认为φu∈[-45°,0°];②当0.5≤ku<0.8 时,US仍可用Uf近似,基于式(6)可知Uf幅值跌落至0.5 |En|时argUf≈ -60°,取一定的裕度,认为φu∈[-75°,-15°];③当0.2≤ku<0.5时,argUS甚至可以达到-85°,在此认为φu∈[-110°,-45°];④当ku<0.2 时,认为φu∈[-110°,-80°]。针对特定容量和电压等级的换流器,将上述φu和ku代入式(1)和式(7)即可计算得到Zm的取值范围。以电压等级为500 kV、容量为300 MW 的换流器为例,Imax取1.5IN,ZT取10 %,该场景下ku> 0.15,结合式(1)和式(7)可得交流线路发生三相故障时,Zm的理论取值范围如图5所示。图中:Rm和Xm分别Zm的实部和虚部。
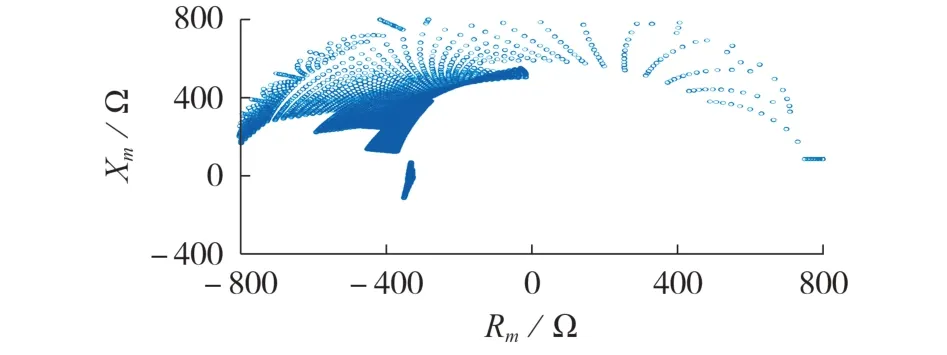
图5 发生三相故障时的换流器等值背侧阻抗Fig.5 Equivalent back impedance of converter during three-phase fault
2)单相接地故障。
以A 相接地故障为例,故障复合序网络如附录A图A4所示,图中:下标1、2、0分别表示正、负、零序分量,后同。设置换流器采用电流平衡控制。基于图A4,Uf1可以表示为式(8)。
式中:ZΣ0为故障点两侧零序阻抗的并联。
当Rf很大时,基于式(8)可知argUf1<0°,此时m侧正序电气量和图A2 相似;当Rf= 0 时,由于系统存在负序和零序支路,Uf1无法严重跌落,argZσ_AG接近90°,argUf1接近0°;当Rf和Zn+Zfn的幅值相近时,故障后的Uf1滞后于故障前。综上所述,在推导换流站单相接地故障对应的背侧阻抗时认为:①当ku≥0.8时,φu∈[-30°,0°];②当0.6 ≤ku< 0.8时,φu∈[-45°,15°]。将上述φu和ku代入式(1)可推导得到Zm1的取值范围如附录A图A5所示。
3 单馈入系统适应性评估
下面对电流差动保护、突变量方向元件、正序电压极化距离保护在图2(a)、(b)所示系统中的适应性进行评估。值得指出的是,考虑到互感器误差具有不确定性,本文忽略了互感器精度对保护的影响。
3.1 电流差动保护
3.1.1 保护原理
基于图2(a)所示的拓扑,当系统发生区内故障时,电流差动保护的动作判据如式(9)所示[1]。
式中:Icd为差动电流;Izd为制动电流;k为制动系数,本文取为0.5;Ix为很小的定值。
3.1.2 适应性分析
1)三相对称故障。
(1)控制策略的影响。对于图2(a)所示的系统,当系统发生区内三相低阻故障时恒成立,不受换流器控制策略和故障位置的影响。此时有Icd≈2Izd,如式(10)所示,因此保护能正确动作。
当系统发生区内三相高阻故障时,电网电压跌落较小,根据式(2)和式(4),U*1≥0.9 p.u.时VSC 和MMC 型换流站控制点处的正序电流和正序电压保持同相位。取极端情况进行分析,对于电压等级为220 kV、传输功率为200 MW 的换流站而言,当系统发生Rf= 246 Ω(由电压有效值除以电流有效值得到)的区内三相故障时,Im基本由故障点分流,In≈0,将Im和In代入式(9)可知Icd≈2Izd,电流差动保护能够正确动作,可见发生三相故障时电流差动保护具有较好的抗过渡电阻能力。
(2)系统参数的影响。基于3.1.1 节可知,传统电流差动保护基于R-L 模型,当线路较长时其分布电容特性可能对保护造成影响,下面对此进行分析。当线路发生区内故障时,由于换流站弱馈,大部分故障场景下,保护性能良好;当系统发生区外故障时,以金属性故障为例,此时Icd和Izd可表示为式(11)所示的形式。
式中:γ为传播系数;l为线路长度。
取我国南方某系统线路阻抗代入式(11),计算得到的Icd、Izd与线路长度的关系如附录A 图A6 所示。当k=0.5 时,若线路长度超过1 000 km,则电流差动保护不会误动,考虑到交流线路长度往往小于300 km,因此可以忽略分布电容对保护的影响。
2)单相接地故障。
以A 相接地故障为例,结合故障边界条件可知区内A 相接地故障下A 相差动电流Icda可以表示为式(12)所示的形式。
式中:Ima和Ina分别为m侧和n侧的A相电流。
默认换流器采用电流平衡控制,m侧负序电流为0,Ima-Ina可以表示为:
当系统发生区内A 相低阻接地故障时,短路电流由零序电流主导,式(13)可以近似为式(14)。由于变压器、传输线和常规系统的零序阻抗相位均接近90°,因此Im0和If0的相位相近,结合式(12)和式(14)可知Ima-Ina的幅值小于Icda,因此Icda>Izda(Izda为A相制动电流),电流差动保护能够正确动作。
而当Rf较大时,零序电流较小,此时Ima-Ina可以近似表示为式(15)。
进一步,由A相接地故障的边界条件可知:
式中:ZΣ0—ZΣ2分别为故障点两侧零、正、负序阻抗的并联[10]。
式(16)中,由于正常运行时沿线电压的相位接近,因此argU[0]f可以近似为0°,代入式(16)可知argIf0∈(-90°,0°),当Rf很大时,argIf0≈ 0°,考虑到此时正序电压跌落小,因此argUm1同样接近0°,根据式(2)—(4)以及第2 章的分析可知,无论是VSC 还是MMC 系统,正序电压跌落较小时argIm1均和argUm1相似,因此argIm1≈argIm0≈ 0°,代入保护判据可知,电流差动保护能够正确动作。
3)相间故障。
以BC相间故障为例,当换流站采用电流平衡控制时,Imb和Imc的幅值相等、相位相差120°,由于相间故障的Rf较小,因此n侧提供的短路电流较大。基于故障点电路可知式(17)成立。
由于换流器弱馈,因此Imb和Imc的幅值较小,结合式(17)可知,Inb和Inc的幅值近似相等、相位相差约180°。忽略Rf,Inb和Inc可以表示为:
式中:Eb和Ec分别为常规系统的B相和C相电动势;Z′为BC相间故障点至常规系统等效阻抗。
式(18)中,argEb= -120°。设argZ′ = 85°,可推得argInb≈ -175°,且因为argEa= 0°,可知正常运行时argU[0]ma≈ 0°。基于故障复合序网络,系统发生BC 相间故障时Uf1可以表示为:
式(19)中,由于换流器具有弱馈特性,-Um1/Im1+Zfm1的幅值往往较大,结合BC 相间故障的边界条件Uf1=Uf2+If1Rf可知,Uf1不会发生严重跌落,且相位跳变较小,这导致Um1故障后相位跳变同样较小。结合上述分析和式(2)—(4),可以绘制出换流器采用不同控制策略且系统发生BC 相间故障时的电气相量如图6所示。
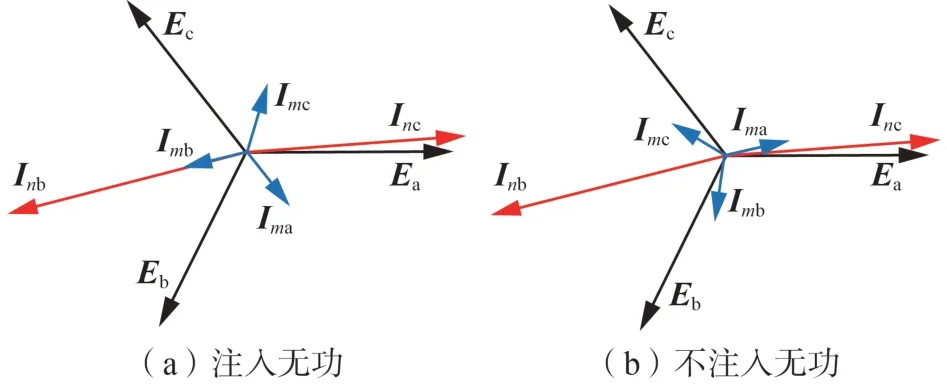
图6 不同控制策略下换流器发生BC相间故障时的电气相量图Fig.6 Phasor diagram of electrical quantities for different control strategies of converters during phase BC fault
由图6(a)可知,当换流器注入无功且系统发生BC 相间故障时,电流差动保护性能较好。而由图6(b)可知,当换流器不注入无功且系统发生BC 相间故障时,C 相两端电流的相位差可能大于90°,电流差动保护的灵敏度下降。对于图6(b)对应的控制策略,以线路近端发生BC 相间金属性故障为例,根据式(19)可知此时Uf1和Um1跌落近50 %,当ZT取15 % 且Imax=2IN时,|Im1ZT|将会造成30 % 的压降,而根据式(2)可知,US1和Im1仍保持同相位,基于图4可推导得到Im1的相位超前Um1近37°,这将使图6(b)中Imc和Inc的相位差接近180°,从而导致电流差动保护的灵敏度下降。
但值得指出的是,当换流站并入强系统时,交流线路发生BC 相间故障时Inc往往远大于Imc,因此Inc的相位对电流差动保护的影响可以忽略,只有在换流站并入弱电网时电流差动保护才会受到影响。
3.2 突变量方向元件
3.2.1 保护原理
由于同步机、传输线的序阻抗相位接近90°,m侧发生正方向故障时,方向判据可设置为:
由式(20)可知,突变量方向元件的最佳适用条件为电力元件等值阻抗呈感性。当m侧发生反方向故障时,易推得交流线路长度小于500 km 时线路分布参数效应对方向元件的影响可以忽略,因此下面主要对m侧发生正方向故障时的正序突变量方向元件的适应性进行研究。
3.2.2 适应性分析
1)三相对称故障。
a)控制策略影响:发生三相高阻故障时,无论换流器采用何种控制策略,m侧的电气相量均和图A2相似,换流站等值正序阻抗呈感性,方向元件能够正确动作。
当换流器注入无功且系统发生三相低阻故障时,由图A3 可知,方向元件可能误判。当换流器不注入无功且系统发生三相低阻故障时,依据式(2)可知Im和US同相位,结合Um=Uf+ImZfm,可推导得到m侧发生近端三相低阻故障时ImZfm的幅值较小,argUm≈ argUf≈ -85°,此时的电气相量如附录A图A7所示。由图可知,方向元件能够进行正确判别。而当系统发生远端三相低阻故障时,Im(Zfm+ZT)的幅值较大,如果Im和US仍保持同相位,则Uf可以近似为US、US1和Uf构成三角形的最长边,因此Uf的幅值应大于Im(Zfm+ZT),这与三相低阻故障是矛盾的,此时依据式(2)所示的控制指令,换流器无法到达稳态工作点,因此换流器在系统发生三相低阻故障时应具备式(21)所示的iq1ref提供能力。
b)系统参数影响:当线路末端含容抗为ZC的串补时[16],区内三相故障下的In可表示为:
基于式(22)可知,当Rf较小且ZC足够大时,argIn>0°,这将导致Uf和Um相位均超前于故障前,此时不同故障穿越控制策略下m侧电气相量图如附录A图A8所示,由图可知,方向元件将发生误判。
2)单相接地故障。
a)控制策略的影响:基于第2 章的序阻抗特征研究可知,发生A相高阻接地故障时,方向元件一般不会发生误判。当系统发生A 相极低阻接地故障时,Um1的相位可能超前于故障前,此时换流器场站侧的正序电气相量和图A8相似,方向元件可能发生误判,特别是对于不注入无功的换流器系统,Um1的相位往往超前Uf1较多,因此故障后Um1的相位超前于故障前的概率更大,方向元件的误判概率更大。
b)系统参数的影响:当线路末端含有串补装置时,Uf1可以表示为式(23),当串补度较高时,Uf1的相位超前于故障前,进而导致Um1的相位超前于故障前,方向元件误判。
3)相间故障和相间接地故障。
相间故障与相间接地故障的分析方法和单相接地故障相似,在此不再赘述。
3.3 正序电压极化距离保护
3.3.1 保护原理
正序电压极化距离保护通过比较补偿电压Uop和极化电压Uref的相位来判别故障位置[17],其中Uop定义为:
式中:Zset为正序电压极化距离保护Ⅰ段整定阻抗。
以三相故障为例,正序电压极化距离保护Ⅰ段的区内故障动作判据为:
3.3.2 适应性分析
1)相间故障。
以BC相间故障为例,Uop和Uref的表达式为:
式中:Umbc和Imbc分别表示m侧BC 相的电压差和电流差。
当系统发生BC 相间金属性故障且换流站采用电流平衡控制时,保护判据可表示为式(28)。依据图1 中的适应性评估方法,当换流器不注入无功时,由于ZT的影响δ> 0°,同时考虑到线路模型匹配度的影响,实际工程中Zfm如式(29)所示。
式中:Zc为传输线波阻抗;d为实际故障位置。
由于分布电容效应的影响,argZfm将小于argZset,综合考虑上述因素后可推导得到发生Ⅰ段区内故障时arg(Uop/Uref)将位于第四象限,正序电压极化距离保护拒动;而当换流器注入无功时,根据式(4)可知,发生BC 相间金属性故障时δ往往小于0°,正序电压极化距离保护能够正确动作。
当Rf≠ 0时,由于换流器的弱馈特性和相间故障的低过渡电阻特性,故障点电流基本由n侧系统提供,此时arg(Uop/Uref)可表示为:
式(30)中,无 论 是MMC 还 是VSC 系 统,arg(If1Rf/Um1)一般在(-90°,0°)范围内,即使Rf较小,对端系统的强助增特性也可能导致Ⅰ段发生区内故障时arg(Uop/Uref)在(-90°,90°)范围内,进而造成正序电压极化距离保护拒动。
2)三相对称故障。
发生Ⅰ段区内三相金属性故障时,电气量满足式(25),保护能够正确动作。
当Rf≠ 0时,正序电压极化距离保护的判据可以转化为:
式(31)中,当Rf很大时,IfRf值很大,而由换流器的弱馈特性可知Im(Zfm-Zset)和ImZfm均较小,因此沿线电压相位近似相等,arg(Uop/Uref) ≈ 0°,Ⅰ段区内发生三相高阻故障时保护拒动。
当Rf较小且换流器不注入无功时,Uop和Um在空间的分布如附录A 图A9(a)所示,发生Ⅰ段区内故障时正序电压极化距离保护拒动。当换流器注入无功且US严重跌落时,Im滞后于Um近90°,ImZset较大时的Uop和Um如附录A图A9(b)所示,可见发生Ⅰ段区内故障时正序电压极化距离不会拒动;而当US没有严重跌落时,m侧电气相量如附录A图A9(c)所示,可见发生区内故障时正序电压极化距离保护将会拒动。
4 多馈入系统适应性评估
基于第3 章和已有研究[9]可知,突变量方向元件、电流序分量选相元件、正序电压极化距离保护在图2(a)、(b)所示系统中存在较明显的适应性问题,因此利用图A1 所示的方法对上述保护元件在图2(c)系统中的适应性进行评估。
4.1 突变量方向元件
对于图2(c)所示的系统,保护安装处背侧阻抗相位θ=arg( )Zm//Zζ与换流站等值阻抗Zm和非故障馈线阻抗Zζ的关系如图7所示[18]。
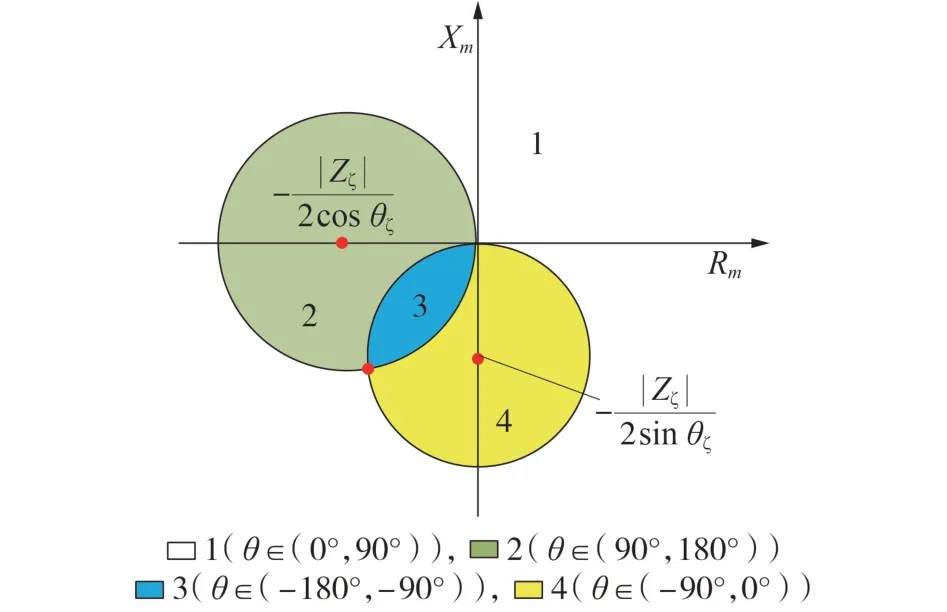
图7 Zm和Zζ与θ的关系Fig.7 Zm and Zζ in relation to θ
以图5中交流系统发生三相故障时对应的Zm波动范围为例,当Zζ较小以致Zm位于附录A 图A10 中的白色区域时,θ∈[0°,180°],方向元件不会发生误判。针对其他类型故障均可采用该方法进行评估。
对于电压等级为500 kV、容量为300 MW、ZT=10 % 的VSC 换流站而言,当式(32)满足时,恒有θ∈[0°,180°],可以将式(32)设置为适应边界。
取θζ=85°,可以将式(32)转化为新能源和非故障馈线相对短路比(short circuit ratio,SCR)rSC的形式,如式(33)所示。
式中:UN为系统额定电压;P为额定功率。
4.2 电流序分量选相元件
对于图2(c)所示的系统,当换流器采用电流平衡控制时,发生A 相接地故障时选相元件不误判的边界为:
式中:arg (Zfn1+Zn1) ≈ 85°,取一定的裕度认为当arg (Zm1//Zζ1)∈(0°,170°)时选相元件不会误判。基于文献[18],可推导得到系统发生A 相接地故障且Zm1位于附录A 图A11 中的白色区域时,选相元件不会发生误判。结合图A5 和图A11 可知,当θζ=85°时,可求得发生A 相接地故障时选相元件不误判对应的边界条件为:
对于其他类型的故障,可以用与A 相接地故障相同的方法求解适应边界,最后对所有类型故障的适应边界取交集即可得到最终的适应边界。对于电压等级为500 kV、容量为300 MW,ZT= 10 % 的换流站而言,可推导得到适应边界如式(36)所示。
4.3 正序电压极化距离保护
基于3.3节的分析可知,不注入无功的换流器系统发生Ⅰ段区内BC 相金属性故障时保护拒动。以ZT=10 %、Imax=1.5IN为例,取一定裕度,认为式(28)中换流站电气量造成的最大误动角δ为25°。对于图2(c)所示的系统,非故障馈线提供的电气量一般能够使正序电压极化距离保护最灵敏地动作,在故障线发生Ⅰ段区内BC相金属性故障时,非故障馈线提供的最小短路电流近似如式(37)所示(假定Zζ1=Zζ2)。
式中:ubc和Ibc分别为非故障馈线BC 两相的电压差和电流差;ZL1为故障馈线的正序线路阻抗。
本文设置u和En相同,当式(38)被满足时,非故障馈线提供的短路电流能够覆盖换流站短路电流对保护的影响。
以ZL1=6+j40.2 Ω为例,可求得适应边界为 |Zζ1|≤1 285(θζ1=85°),将其转化为短路比的形式可以表示为rSC>0.65。
5 性能提升方案
基于第2 章中的故障特性分析及第3 章中的适应性评估结论,提出2 种通过调整保护判据提升保护性能的方案。
5.1 方向元件性能提升方案
由3.2节可知,换流器系统正方向发生三相故障时,argZm1可能大于180°,argZm1取值的极端情况通常为线路远端发生三相极低阻故障,此时受系统拓扑的限制,Im滞后Um近90°,而Um的取值比线路近端发生三相极低阻故障时要大,结合图A3可知此时argZm1较大。基于此,可以对保护判据进行补偿以提升发生三相故障时保护元件的性能,如式(39)所示。
式中:λ为补偿量,可通过线路远端发生三相极低阻故障时arg( -ΔUm/ΔIm)的相位进行估算。
5.2 距离保护性能提升方案
对于正序电压极化距离保护,当不注入无功的换流器系统发生相间故障时,可以对保护判据添加补偿量γ以提升保护性能,如式(40)所示。
γ的选择与系统参数、控制策略、Rf有关。以BC相间金属性故障为例给出γ的设置方法:当ZT=15 %、Imax=2IN时,发生故障时ZT造成的压降为0.3UN;依据故障序网络可推导得到发生近端BC 相间金属性故障时|Um|≈0.5UN、δ≈arcsin 0.6≈37°,发生远端B相间C金属性故障时δ可能更大,该场景下可以将γ设置为 -50°。
6 仿真验证
为了验证保护适应性分析的正确性和优化方案的有效性研究的有效性,利用电磁暂态仿真中广泛使用的PSCAD 软件[19]搭建了电压等级500 kV 的MMC系统模型,模型参数如附录B表B1所示。系统频率设置为50 Hz,采样频率为10 kHz,线路采用贝瑞隆模型。同时,为了保持其他变量一致以分析控制策略对保护的影响,在MMC 系统模型中设计了2 套控制策略,即式(2)和式(3)、(4)所示的控制策略,控制点均位于变压器前。
6.1 换流站序阻抗特征验证
本节设置MMC 系统采用式(3)、(4)对应控制策略,对不同故障场景下换流站的等值背侧阻抗进行仿真计算,结果如表1 所示。由表可见,A 相接地和三相故障下Zm1的取值与图5、图A5 中的数据能够对应。
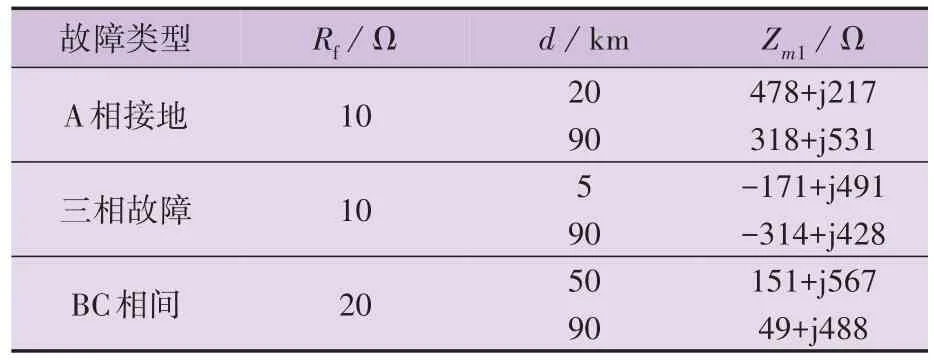
表1 换流站注入无功时的等值正序阻抗Table 1 Equivalent positive-sequence impedance of converter station when converter injects reactive power
6.2 单馈入系统验证
本节对换流器单馈入系统中传统保护的适应性进行了验证,限于篇幅,仅给出三相故障、单相故障以及BC相间故障对应的仿真结果。
1)电流差动保护。
对不同场景下的交流故障进行仿真验证并取稳态数据进行计算,20 ms 时线路5 km 处发生BC 相间故障(Rf= 20 Ω)的计算结果如附录B 图B1所示。由图可知,当换流器并入强系统时,B、C 相电流差动保护均能正确动作,但当换流站注入无功时C 相电流差动保护的灵敏度更优。
不同控制策略下系统发生单相接地和三相故障时电流差动保护的动作情况如附录B 表B2、B3 所示。由表可见,电流差动保护能够正确动作。
2)突变量方向元件。
对不同故障场景下突变量方向元件的性能进行仿真验证,结果如附录B 表B4、B5 所示。由表可见:若线路不含串补,则正序突变量方向元件在发生高阻故障时一般不会误判;若线路末端含有串补度为40 % 的串补,则线路90 km 处发生不同类型故障时,正序突变量方向元件均会误判,且argZm1位于[-173.8°,-120.5°]范围内,难以通过调整保护判据改善保护性能。
3)正序电压极化距离保护。
不同故障场景下正序电压极化距离保护的计算结果如附录B 表B6、B7 所示,表中Zset取线路阻抗的85 %。由表可见:当系统发生A 相低阻接地故障时,保护性能较好,但当Rf达到300 Ω 时,无论故障位置如何arg( )Uop/Uref均接近0°,区内A 相接地故障下正序电压极化距离保护拒动;当系统发生三相故障时,保护耐过渡电阻能力差,即使Rf仅为10 Ω,线路20 km 处发生故障时保护仍会拒动;当系统发生BC相间故障时,保护耐过渡电阻能力同样极差,此时可基于式(40)对保护判据进行补偿,在此设置ζ=-50°,代入表中数据可见保护的性能有所改善。
6.3 多馈入系统验证
基于第4 章推导得到的保护适应边界,在MMC模型侧并入u=500∠0° kV、Zζ=30+j620 Ω 的同步机系统,设置MMC 采用式(3)、(4)对应的控制策略,检测保护安装处正序突变量方向元件和电流序分量选相元件的性能,部分仿真结果如附录B 表B8 所示,由表可见,保护元件不会误判。
随后针对正序电压极化距离保护,在MMC 侧并入u=500∠0° kV、Zζ=85+j1 000 Ω 的同步机系统,设置MMC 采用式(2)所示的控制策略,设置不同位置发生Rf= 0.1 Ω 的BC 相间故障,保护动作结果如附录B表B9所示,可见保护不会误动或拒动。
7 结论
本文对传统交流线路保护在换流器并网系统中的适应性进行了评估,给出了部分保护在交直流多馈入系统的适应边界,针对部分存在适应性问题的保护提出了改进方案,具体结论如下。
1)评估保护适应性时,应综合考虑模型匹配度、互感器精度、系统参数等因素对被保护元件故障特征的影响。
2)当换流器并入弱系统且只注入有功电流时,相间故障场景下电流差动保护灵敏度下降。
3)系统发生三相低阻故障且换流器只注入无功时,正序突变量方向元件可能误判,此时可通过扩大保护判据以提升保护性能;当系统发生不对称低阻故障且换流器只注入有功时,方向元件误判概率增大。当线路末端含串补时,远端故障时方向元件大概率误判。
4)系统发生三相故障时正序电压极化距离保护耐过渡能力差,只有过渡电阻很小、且换流器采用“零有功,注无功”策略时保护才可能具有较好的性能;当系统发生相间金属性故障时,受变压器参数和换流器控制策略的影响,发生Ⅰ段区内故障且换流器不注入无功时保护易拒动,此时可以通过调整保护判据提升保护性能。
5)在交直流多馈入系统中,当非故障馈线系统的参数/源特性满足适应边界时,保护能够正确动作,可以将其作为适应性评估的定量指标。
6)现有故障穿越策略存在改进空间,特别是当MMC 发生三相低阻故障时,换流器控制策略应具备自动调节参考值的能力以满足电路拓扑。
本文在已有研究的基础上更着重考虑了系统实际参数等因素对保护的影响,所得结论更适用于实际工程,但仍存在巨大的改进空间,例如:对于新能源汇集系统的处理目前仍将其等效为单机,并没有考虑规模化新能源机组工作点不一致、内部存在交互的问题;当系统为100 % 新能源系统时,故障后电气量的变化规律以及保护适应性问题仍有待探索;当换流器在不对称故障期间吸收负序电流时,保护适应性是否会受到影响还尚未分析。后续将对上述问题进行研究。
附录见本刊网络版(http://www.epae.cn)。
