基于粒子群差分进化极限学习机的电力系统故障诊断模型

张 耀,姚 瑶,陈 卓,袁子霞,熊国江

(1.贵州电网有限责任公司电力调度控制中心,贵州 贵阳 550002;2.贵州大学电气工程学院,贵州 贵阳 550025)

0 引言

电力系统故障诊断(fault section diagnosis,FSD)是指通过数据采集系统(supervisory control and data acquisition,SCADA)得到的保护继电器(protective relays,PRs)和断路器(circuit breakers,CBs)动作与否的信息来识别故障区段[1]。在电力系统发生故障时,首要的是隔离故障,降低事故范围,解决故障,从而实现快速恢复供电。因此,对故障实现快速准确的诊断至关重要。当区段发生故障时,首先是其对应的主保护继电器运行,使得相应的断路器跳闸,从而隔离故障,降低故障范围。在隔离故障的过程中,继电保护系统的动作存在不确定性,如果主保护继电器或者其对应的断路器由于某些原因未正确动作,则激活其后备保护以隔离故障。但是在实际过程中,继电器和断路器都会存在误操作、误动作的可能性,从而导致不确定性增加,这些不确定性会使得FSD的诊断准确率和效率大大降低。针对此类问题,有很多学者提出了不同的方法来解决。

现如今,主要的FSD方法主要包括专家系统[2-4]、贝叶斯网络[5-7]、Petri网[8-10]、解析模型[11]和神经网络[12-14]等。基于专家系统的FSD方法通过模拟专家的逻辑建立规则库,通过与规则库的对比实现故障诊断,但是针对大规模电网,建立和更新规则库都面临着巨大的困难。基于贝叶斯网络和Petri网的FSD方法都能够比较直观地揭示诊断过程,具有较好的解释性,但是此类方法容错率较低,面对复杂故障时常常无法正确诊断。基于解析模型的FSD方法的诊断性能依赖于算法的性能和所构建模型的完整性。这些方法在FSD问题上都各有优势,但是根据无免费午餐定理,如何不断提高诊断性能仍然存在很多可探索的方向。

神经网络方法在解决FSD问题上,由于其容错性好、诊断效率高、泛化能力强等特点成为热点研究对象。文献[12]通过将遗传算法与BP神经网络结合来解决FSD问题,但BP神经网络容易陷入局部最优;为解决这个问题,文献[13]提出将模糊集理论与径向基函数神经网络RBF相结合用于该问题;为了适应电网拓扑结构变化,文献[14]针对电力系统中的元件(线路、变压器、母线)建立RBF神经网络。

常用的神经网络如BP神经网络、RBF神经网络都有一个共同的问题,即神经网络的内部连接权值和阈值需要根据当前模型的输出值不停地进行调整,当电力系统规模较小时,诊断故障的时间较短,但是当电力系统规模增大时,不停地对参数进行调整则会浪费掉很多时间[15]。而极限学习机(extreme learning machine,ELM)[16]神经网络可以避免这个问题,因为ELM的部分权重和阈值只需要在初始化阶段随机给定,在整个诊断过程中不需要对其再进行循环调整,这在极大程度上解决了其他常用神经网络需要不停调整参数的问题。

但是ELM神经网络的隐含层神经元个数需要提前给定,隐含层神经元个数过少则泛化能力不够,不能正确诊断出故障,如果过多则会导致过拟合且浪费计算资源。对此,本文选用进化算法对隐含层神经元个数进行寻优。粒子群算法(particle swarm optimization,PSO)[17]和差分进化(differential evolution,DE)算法[18]是最常用的进化算法,但是基本PSO容易陷入局部最优,而DE算法收敛精度不高。考虑到两者具有互补的优势,本文提出采用一种多重随机变异的粒子群差分进化算法(particle swarm differential evolution with multiple random mutation,MRPSODE)来提高ELM隐含层神经元个数的寻优能力。MRPSODE在DE的基础上加入了PSO的策略,可以很好地实现优势互补,从而克服两者的不足[19]。考虑到原始故障样本数据可能遭受到噪声的干扰,影响样本质量,本文采用交叉验证方法对样本数据进行处理,降低噪声对最终实验结果的影响。最后通过仿真对比分析验证了所提FSD方法的诊断性能。

1 极限学习机

ELM作为一种简单但效果良好的机器学习技术,在大数据时代得到了广泛的应用。同时,ELM是针对单隐层前馈网络的有效解决方案之一,其具有学习速度快、泛化能力强和学习精度好等特点。传统的神经网络算法常常需要对内部参数进行大量的计算,如传统的BP算法需要在模型的训练过程中根据网络的期望输出和实际输出之间的差值不断调整权重值,但容易陷入局部寻优。而ELM作为单隐层前馈神经网络,随机生成隐含层的参数,在模型的训练过程中不需要调整,即ELM在获取训练样本之前就可以实现隐藏节点的建立[20]。理论上,ELM即使不更新隐藏层的参数,也能保持其通用逼近能力[21],因此不像传统的基于反向传播BP神经网络容易产生局部最优,同时ELM的最小二乘问题的求解速度比传统BP的梯度方法以及标准向量机的二次规划问题快很多。因此,ELM的泛化性能更好,学习速度更快。ELM的结构如图1所示,n为输入层节点数,m为输出层节点数。

图1 ELM结构

假设具有L个隐藏节点,N个训练样本,隐含层激活函数为p(·)的ELM可表示为

(1)

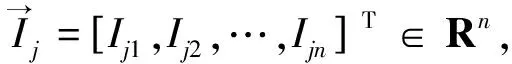
上述方程可以简写为

Hβ=O

(2)

H被称为ELM的隐藏层输出矩阵。ELM可以通过求解式(3)的最小二乘解得到唯一解。

(3)

求解式(3)可得

β=H†O

(4)

式中:H†为矩阵H的广义逆矩阵。

综上,在已确定L个隐藏节点的基础上,ELM可以总结为以下步骤:

a.随机分配隐含层节点参数(输入权值和阈值)。

b.利用激活函数计算隐含层的输出。

c.利用最小二乘法计算输出权重,解析确定输出层的权重。

2 MRPSODE

2.1 粒子群算法(PSO)

PSO受鸟类获取食物的启发在1995年被提出。具有NP个粒子的种群在给定D维解空间被随机初始化,通过适应度函数评估每个粒子的适应度值,在第t代第i个粒子的速度和位置状态属性更新为:

vi,t+1=ρ·vi,t+c1·rand1·(pbest,t-xi,t)+

c2·rand2·(gbest,t-xi,t)

(5)

xi,t+1=xi,t+vi,t+1

(6)

在迭代过程中,每个粒子根据当前的个体极值最优pbest和全局最优gbest更新其速度和位置,以便寻找到最优解。其中,ρ为权重因子;c1、c2为学习因子;rand1、rand2为[0,1]内随机生成的实数。

2.2 差分进化(DE)算法

DE算法经过变异、交叉和选择过程完成种群进化。

a.变异。DE算法采用变异操作针对每个目标向量xi,t生成突变向量ki,t+1。其中一种常用的变异策略DE/current-to-rand/1为

ki,t+1=xi,t+F·(xr1,t-xi,t)+F·(xr2,t-xr3,t)

(7)

式中:r1、r2、r3为互斥整数;F为缩放因子。

b.交叉。将目标向量xi,t和突变向量ki,t+1混合,通过交叉得到试验向量ui,t+1,即

(8)

式中:j=1,2,…,D;CR为交叉概率。

c.选择。通过计算目标向量xi,t和突变向量ki,t+1的适应度值,较小者保存进下一代中,即

(9)

2.3 多重随机变异粒子群差分进化算法(MRPSODE)

MRPSODE是基于DE算法提出的一种改进算法,它有效解决了基本DE算法收敛缓慢而导致收敛精度不高的问题。MRPSODE将PSO的更新策略引入DE算法中,从而实现全局收敛能力的提高,同时选用DE/current-to-rand/1的突变策略增加种群多样性避免陷入局部最优[19]。为了平衡算法的探索和开放能力,MRPSODE结合了3种变异策略,3种变异策略可以有效地发挥各自的优势,弥补其他策略的不足,从而具有良好稳定性和收敛性的同时保证种群多样性。针对每个个体,MRPSODE采用参数Pr(取值0.9)和RM(0和1之间随机数)来确定该个体所采用的变异策略:

a.如果某个随机数rand小于概率参数Pr,且RM小于0.5,则

(10)

b.如果某个随机数rand小于概率参数Pr,且RM不小于0.5,则

ki,t+1=xi,t+F·(xr1,t-xi,t)+F·(xr2,t-xr3,t)

(11)

c.否则,有

ki,t+1=xmin+rand·(xmax-xmin)

(12)

式中:xmin和xmax分别为个体位置下限和上限。

值得说明的是,除了变异策略选择机制外,MRPSODE的其余部分与基本DE保持一致。

3 基于MRPSODE的ELM模型

ELM的输入输出取决于具体的仿真案例,权重和阈值在初始化阶段被随机给定,所以ELM还有一个重要的参数需要给定,那就是隐含层的节点数目。为了确定最佳的隐含层节点数目,常常采用在取值范围内进行试错的方法。当取值范围很大时试错法需要对每个可能取值进行计算,整个计算过程需要花费很多时间和精力。而利用进化算法可以比较方便快速地确定不同模型中最佳的隐含层节点数目。本文利用MRPSODE对ELM隐含层节点数目进行确定,选用均方根误差(RMSE)作为适应度函数,即

(13)

基于MRPSODE确定ELM故障诊断模型的最佳隐含层节点数目的流程如图2所示。根据电力系统网络结构和保护系统配置提取故障训练样本;然后采用MRPSODE自动确定ELM的最佳隐含层节点数目,完成故障诊断模型的构建;故障发生后,通过运行ELM模型实现故障诊断。

图2 基于MRPSODE的ELM模型构建流程

考虑到训练样本中可能包含噪声数据,会影响到ELM网络的准确率,为了提高系统的准确率,降低噪声数据对最终实验结果的影响,本文选择使用5折交叉验证方法对训练样本进行处理。将训练数据划分为互不相交的5等份,如图3所示。每1行代表1折交叉验证,由于本文选择使用5折交叉验证方法,所以共有5行。每行把数据分为5份,每份数据所占总数据的比例为20%。如本文所选用的样本数据共60条,每个框代表里面共有12条样本。在训练过程中,每次选其中1份作为验证数据集(图中浅色部分),其他4份作为训练数据集(图中深色部分)。通过交叉验证,可以尽可能地降低噪声数据的影响,提高ELM的容错能力。

表1 测试系统的实验结果

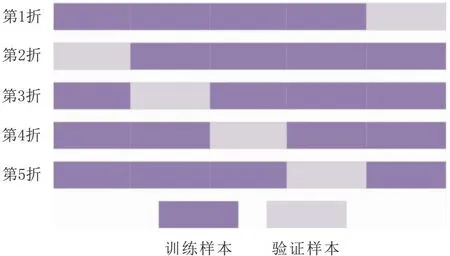
图3 交叉验证数据划分

4 算例仿真

本文采用中国吉林省四平电网发生的真实故障案例[11]来验证所提出的故障诊断方法。相关的电力系统结构如图4所示。B2母线出现故障,主保护B2m拒动,相应的后备保护L1Rs、L3Rs、L4Ss动作,使得断路器8204、1504、3104跳闸;同时B7母线出现故障,主保护B7m动作,断路器4803、4811、4802跳闸,而断路器4801拒动,断路器3170跳闸,受故障电流的影响断路器3106跳闸。

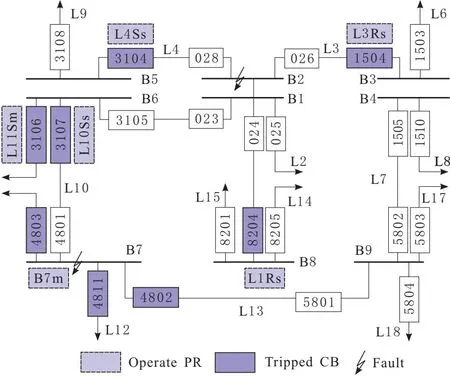
图4 吉林四平结构

本文根据图4构造了60条故障数据。样本的特征项为图中线路和母线的主保护、近后备保护、远后备保护以及断路器的动作状态。保护或者断路器动作,其特征值为1;若保护或者断路器未动作,其特征值为0。神经网络的输出即为线路和母线的故障可能性,大于0.5即认为故障,否则为无故障。故障模式包括“故障”和“无故障”2种模式。由于案例为实际故障,只有1条实际故障信息,所以本文独立运行100次,以正确诊断出故障的次数除以100作为诊断正确率。由于隐含层的节点个数必须为整数,所以最终的隐含层节点个数为独立运行100次交叉验证得出的结果求平均值,再向上取整。设定种群个体数为10,迭代次数为20,ELM隐含层神经元个数的范围为[1,80]。为了验证MRPSODE的有效性,将其与DE和PSO进行对比。3个算法的收敛曲线如图5所示。图5中,MRPSODE-ELM的收敛速度明显快于DE-ELM和PSO-ELM,且能够获得最小的适应度值RMSE,表明利用MRPSODE对ELM隐含层节点个数进行优化相比于其他对比算法更具竞争力。

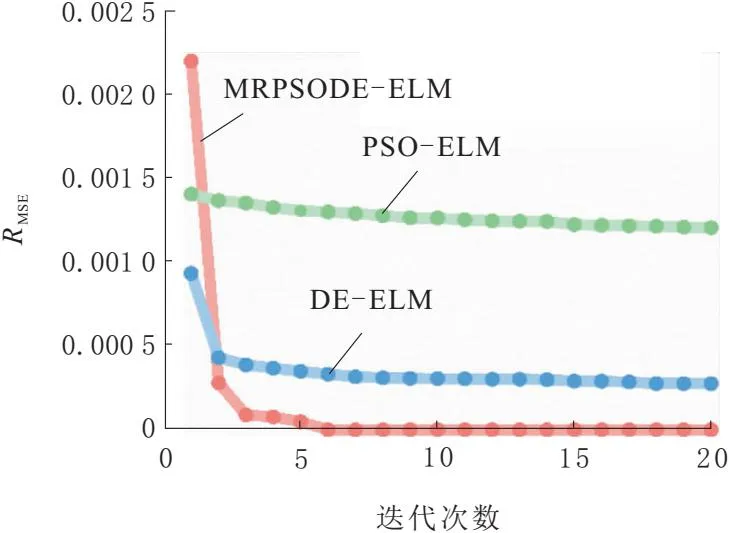
图5 迭代收敛对比

经过100次5折交叉验证得到的隐含层神经元个数平均值为74.686,但是神经元个数不能为小数,必须是一个整数,所以对求出的平均值进行向上取整,即在该测试案例中最佳的隐含层神经元个数为75。为了验证经过MRPSODE优化的ELM的诊断性能,将其与BP神经网络和RBF神经网络进行对比。本文设定BP神经网络隐含层个数为75,RBF神经网络搜索过程中隐含层节点最大值为75,独立运行100次计算诊断正确率,其实验结果如表1所示。

由表1可知,在相同结构规模的网络中,经过优化后的ELM的诊断正确率最高,达到了93%,BP神经网络最低,为86%,证明了基于MRPSODE的ELM具有更好的诊断性能。

5 结束语

为了提高处理电力系统故障中不确定性的诊断能力,本文提出了一种基于MRPSODE训练的最优ELM诊断方法。采用实际发生的电力系统故障案例来验证该方法。仿真结果表明,所采用的MRPSODE能够确定ELM最佳的隐含层节点个数。在吉林省四平电力系统实际案例中,通过与其他常用神经网络对比,ELM模型诊断的正确率达到93%,说明了所提出方法在复杂故障方面具有较强的诊断能力。

通过仿真也发现,尽管该ELM的正确率达到了93%,但仍然具有可提升的空间。下一步将继续对进化算法深入改进,不断提升ELM的泛化能力,以便在故障诊断问题上获得更好的性能;另一方面,将所构建的ELM模型应用于更多的实际故障场景。