面向分布式光伏并网的自适应距离保护策略

张 钰,王 娜,王鹏飞,戴建华,潘功银,马梦真

(内蒙古电力(集团)有限责任公司包头供电公司,内蒙古 包头 014030)

0 引言

随着风电、光伏等可再生发电在传统电网中的占比逐渐增加,这类机组对电网继电保护的影响和保护策略研究成为热点内容。由于光伏电站具有弱电源特性,故障发生时过渡电阻对线路距离保护的影响更为严重[1],因此,本文针对含有光伏电站的线路距离保护进行分析。目前,对过渡电阻影响分析的方法主要有传统方法、自适应方法和神经网络方法[2],本文利用自适应方法对距离保护展开分析。

目前针对含光伏的保护,文献[3]提出了含高比例分布式光伏的中低压配电网继电保护方法;文献[4]研究了基于故障穿越特性的光伏直流输电线路保护;文献[5]研究了针对光伏场站送出线路不对称短路故障的自适应距离保护原理;文献[6]研究了分布式光伏电站接入系统后的继电保护配置;文献[7]分析了光伏电站中集电线路保护定值整定计算。

另外,针对自适应距离保护,文献[8]提出了考虑分布式逆变电源特性的距离Ⅱ段自适应保护整定方案;文献[9]研究了基于故障电流的距离保护加速动作判据;文献[10]研究了基于模糊匹配的继电保护定值比对。可见自适应距离保护较适用于含有分布式电源的网络中,但目前针对光伏的自适应距离保护研究较少。

本文建立了可再生能源及负荷需求响应模型,以2阶段优化模型为目标,进行模型求解,提出改进求解算法,并利用仿真分析验证了本文所提模型和算法的有效性。

1 光伏系统距离保护模型

1.1 光伏联网系统模型

考虑典型的含有光伏机组的输电线路模型,如图1所示。该线路在S和R节点装有距离保护。ES和ZS为光伏机组机端电压和等值阻抗;ER和ZR分别为系统的戴维南等值参数。

与系统侧保护RR不同,光伏机组的参数会发生变动,影响RS的取值。假设在距离RS处x的距离发生A相接地,RS的计算阻抗为:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

式中:VAS和IAS为RS的A相电压和电流量测值;K0为零序补偿因子;Z1L和Z0L分别为线路SR的正序和零序阻抗;ΔZ为故障阻抗引起的误差;Z为RS量测的等值阻抗;Z0T为光伏变压器等值零序阻抗;D0、D1、D2分别为零序、正序、负序分布因子。

1.2 光伏电站送出线路距离保护的影响

当送出线路区内发生经过渡电阻RF的短路故障,光伏电站侧距离保护测量阻抗为

(8)

式中:θ为故障后系统侧电流和光伏电站侧电流的相位差;m为相应量的量测值;RF为故障过渡电阻;Zk为故障点到保护安装处的阻抗;IS和IPV分别为系统侧电流和光伏电站侧电流。

从图2中可以看出,光伏电站的相位角与控制策略有关,同以往的双侧电源不同,其角度会发生变化,通常介于-180°～180°之间。另外,由于光伏电站具有较明显的弱电源特性,体现为光伏电站整体短路容量较小,因此,在光伏逆变器电流限制的条件下,系统侧电流较光伏侧电流大很多,这会导致光伏侧相角改变而量测阻抗的灵敏度较低,尤其是发生区内过渡电阻较为明显的短路时,会造成距离保护拒动。在图2中,β表示保护线路阻抗的阻抗角,而γ表示传统距离保护测量阻抗的阻抗角。

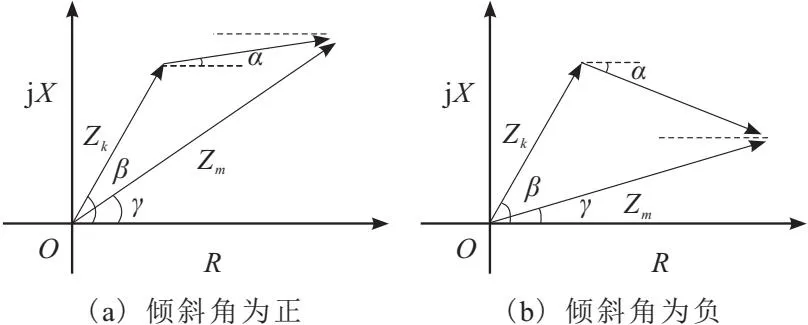
图2 光伏参数特性

1.3 单端和双端距离保护模型

双端距离保护模型按照图1所示的双端系统,距离保护量测阻抗计算如式(8)所示。测距方法根据使用的电气量不同分为单端测距和双端测距。

其中,单端测距的公式为:

(9)

(10)

双端测距的公式为

(11)

2 自适应距离保护模型

2.1 测距模型

如前所述,光伏电站的等值电源阻抗会影响RS的计算阻抗,尤其是在单相接地故障中误差更为明显。并且在多数情况下,过渡阻抗RF不为0。为了消除RF对测距的影响,本文提出自适应距离保护算法。由于正序网络可适用于对称和不对称故障,因此本文选用正序网络进行分析,原理如图3所示。

图3 光伏序网

若由于RF引起的附加阻抗ΔZ可计算得到,则S端量测的阻抗为

(12)

利用基尔霍夫定律,式(12)转化为

(13)

由此可以看出,式(13)与RF无关。利用双端测距电气量可以得到最终结果。

若利用单端测距,则:

V1R=E1R-Z1RI1R

(14)

(15)

2.2 测距参数计算

其中,E1R和Z1R的获取是难点,本文选择的自适应方法的参数等效如图4所示。

图4 参数等效

Z1R=Zth-Z1L

(16)

E1R=Eth

(17)

则Z1R和E1R可仅用S端的量测获得。

计算I1R时,由于x应为实数,则有

(18)

整理得到:

(19)

(20)

式中:K1～K4均为量测系数。

为推导I1R,本文考虑A相接地故障,则有:

IF=I0F+I1F+I2F=3I1F

(21)

I1F=I1S+I1R

(22)

I1F的相角β计算式为

(23)

最终由式(18)得到

(24)

则式(19)转化为求解

(25)

则最终可得I1R的值。

3 算例分析

3.1 系统说明

利用如图5所示系统进行仿真。光伏阵列数为60,光照辐射强度为1 000 W/m2。单个光伏输出功率为1.667 MV·A,箱变为150 MV·A,XT=0.06 pu。线路11-10的正序阻抗为20.625Ω,零序阻抗为65.88 Ω,线路长度为80 km,正序电容为7.05 nF/km,零序电容为4.68 nF/km。

图5 IEEE 33节点系统

3.2 仿真分析

假设在距离RS为0.75 pu处发生A相接地,表1给出了不同故障电阻下的测试结果。表1中,按照继电保护研究惯例,故障点位置用距离上级保护的位置百分数表示,故障类型分为A相接地(AG)、BC两相短路(BC)、BC两相接地短路(BCG)、ABC三相短路(ABC)。

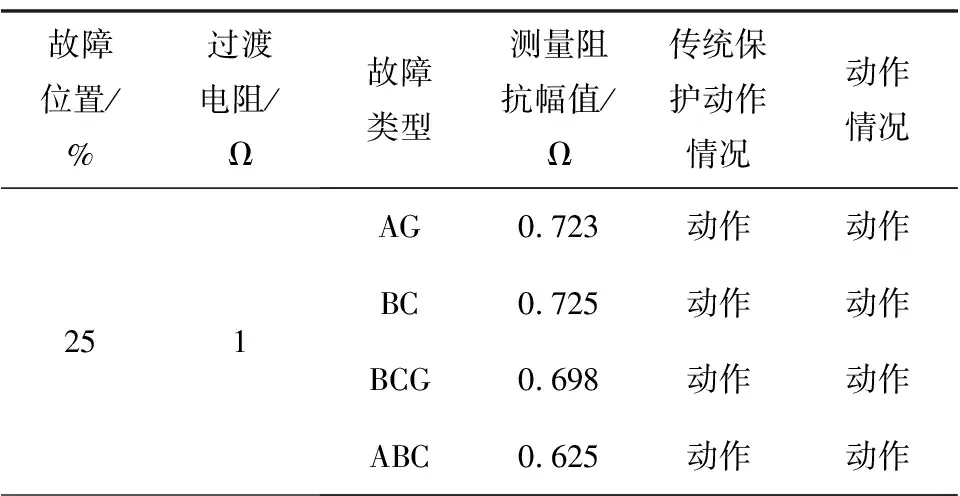
表1 故障判断结果

从表1可以看出,在传统保护机制中,可以检测1 Ω的过渡电阻故障,但10 Ω、30 Ω、100 Ω的过渡电阻检测失效。而本文方法则能够有效检测各种过渡电阻的情况。

分析线路10-11故障后的故障距离计算结果,可以看出故障距离x的计算准确度较高。根据本文模型,故障过渡电阻对本文模型影响不大。

由于光伏系统参数对故障测距有较大影响,本文针对10-11线路上0.6 pu距离的30 Ω过渡电阻进行分析,光伏电站的输出分别为100 MW、50 MW、25 MW,得到的结果如图6所示。

图6 光伏机组参数对故障距离的影响

从图6可以看出,光伏阵列的输出对故障测距的准确性影响不大,表明本文方法的鲁棒性较强。

总体来说,本文采用自适应距离保护,能够有效改善受过度电阻影响较大的误触发距离保护动作的现象。使用本文方法后,送出线路光伏电站侧的距离保护能够在区内不同位置发生不同类型的经过渡电阻短路故障后正确动作,其抵御过渡电阻的能力得到显著增强,动作性能也得到明显改善。

4 结束语

本文提出一种基于自适应距离保护的光伏系统保护模型。通过本文的研究,说明了在含有光伏电站等条件下距离保护的判断方法,并根据仿真分析论证了本文所提模型的有效性。研究结果表明,在这种机制下,光伏参数的变化不会对系统造成影响。此模型能够有效解决过渡电阻对距离保护的显著影响,从而提高了保护系统的稳定性。