基于改进GCC算法的交流配电电缆局部放电在线定位方法研究

肖小龙,郭佳豪,郭茂森,杨景刚,许佳杰,方 鑫,史明明,刘 洋

(1.国网江苏省电力有限公司电力科学研究院,江苏 南京 210008;2.东南大学电气工程学院,江苏 南京 210096;3.国网江苏省电力有限公司,江苏 南京 210024)

0 引言

交联聚乙烯(XLPE)电缆由于其良好的绝缘特性和稳定的机械性能,自20世纪90年代后被普遍应用于各电压等级的配电网中[1-2]。然而,由于设备老化或外力破坏等影响,电缆的XLPE绝缘层中会产生空隙、杂质和气泡等缺陷,引发局部放电现象。长期局部放电会导致电缆绝缘层出现劣化,严重时可能会导致绝缘击穿。因此,为确保电网的安全和稳定运行,对XLPE电缆的局部放电进行在线监测非常重要,可以及时定位和纠正局部缺陷[3-4],有助于消除潜在的故障隐患,从而提高系统可靠性。

专家学者广泛研究了电缆局部放电的定位问题[5-7],文献[8]提出了正弦波时域反射(TDR)方法,文献[9]提出了另一种基于分段相关的多端局部放电定位算法。此外,文献[10]提出利用入射波和反射波信号的交叉傅里叶谱密度函数进行定位,在信号频域中估计缺陷位置,减少了定位脉冲波形失真的影响。这些方法在实际应用中具有一定的局限性[11-12],由于电磁噪声的影响和对局部放电脉冲波速频率特性的忽视,定位结果很容易与现场的实际情况产生很大的偏差[13]。

因此,本文提出一种面向工程实际应用的电缆局部放电在线定位方法。

1 改进GCC算法的电缆局放在线定位方法

1.1 广义相关时延估计

广义互相关时延估计(generalized cross-correlation,GCC)方法通过对2个信号的互功率谱密度函数进行加权,以达到提高2个信号时延精度的目的。其原理如图1所示。

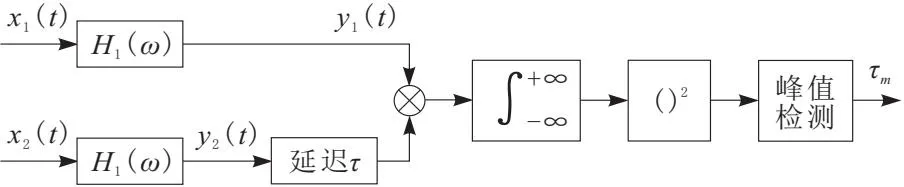
图1 GCC时延估计原理

其中,输出y1、y2之间的互谱密度函数为

(1)

则互相关函数为

(2)

在GCC方法中,通过对2个时延信号的功率谱进行加权计算,减少了外界信号对于互相关函数的影响。加权函数W(f)增大了信号干扰较小处的频谱幅值,突出了互相关函数的峰值相对位置。GCC函数及其权函数如表1所示。

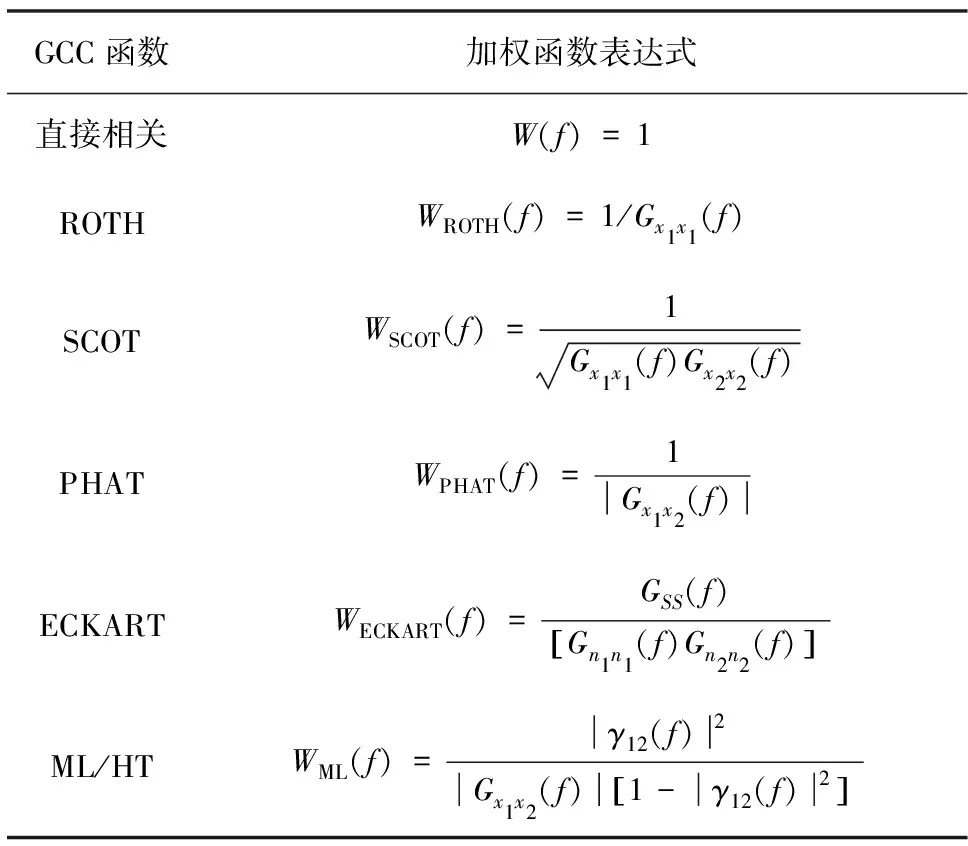
表1 GCC函数及其权函数表达式

其中,γ12为

(3)

1.2 基于改进GCC算法的电缆局放在线定位方法

目前,GCC算法已经逐步应用于电缆的局部放电定位研究中,但由于GCC算法存在缺陷,因此在应用中无法达到预期效果,其主要问题表现为:低信噪比条件下定位精度降低、未考虑波速频率特性对定位精度的影响及部分干扰信号对在线定位精度的影响等。

针对这些问题,本文提出一种改进GCC算法,用于对电缆中的局部放电信号进行检测,提高定位精度,方法流程如图2所示。

图2 基于改进GCC的电缆局放定位流程

1.3 修剪均值数据滤波算法

现场的电缆局放检测环境复杂多变,在对电缆进行局放定位时常伴随高频通信电磁干扰,影响定位结果。此外,局放检测仪的采样频率也是制约局放检测定位精度的关键因素。因此本文提出修剪均值数据滤波技术,通过构造3层数据过滤器,即修剪过滤器、聚类过滤器和平均过滤器,剔除检测到的坏数据,实现多样本局放定位结果的精确估计。

首先,利用修剪过滤器将局放定位结果样本从局部放电(PD)位置最小值到最大值进行排序,筛选定位样本中25%～75%的样本作为下一个过滤器的输入。修剪过滤器通过修剪剔除异常值充当定位样本的第1层过滤器。

其次,采用密度最大值聚类(maximum density clustering application,MDCA)算法作为第2层聚类过滤器。MDCA算法基于密度的思想引入划分聚类中,使用密度而不是初始点作为考察簇归属情况的依据,能够自动确定簇数量并发现任意形状的簇。MDCA的具体步骤如下:

a.计算样本集中第i个数据点,以dc为截断距离的局部密度ρi,即:

(4)

(5)

b.计算每个数据点到高局部密度点距离δi为

(6)

c.在ρ-δ图谱中,选取具有较大局部密度ρ和较大高局部密度点距离δ的数据点作为簇类中心,选取具有较小局部密度ρ和较大高局部密度点距离δ的数据点作为数据异常点。

最后,采用平均过滤器计算簇类中的定位样本平均值,作为最终的电缆局放在线定位结果。

2 基于改进GCC算法局部定位仿真

2.1 基于改进GCC方法的仿真

为了验证本文所提定位方法的有效性,在MATLAB Simulink中开展局放定位仿真试验。以型号为单芯8.7/10 kV 50 mm2YJV中压配电电缆为研究对象,搭建1根2 000 m的电缆模型,仿真参数[14]如表2所示。

表2 仿真电缆参数

在仿真中假设在端点B发生局部放电,向其注入局放仿真信号,在端点A通过示波器测量局放信号波形,端点A通过波阻抗接地,电缆长度Lac=1 200 m,Lbc=800 m,信号幅值A取6 mV,衰减系数τ为1.25 μs,振荡频率fc为5 MHz,采样频率为100 MHz,持续时间20 μs,如图3所示。

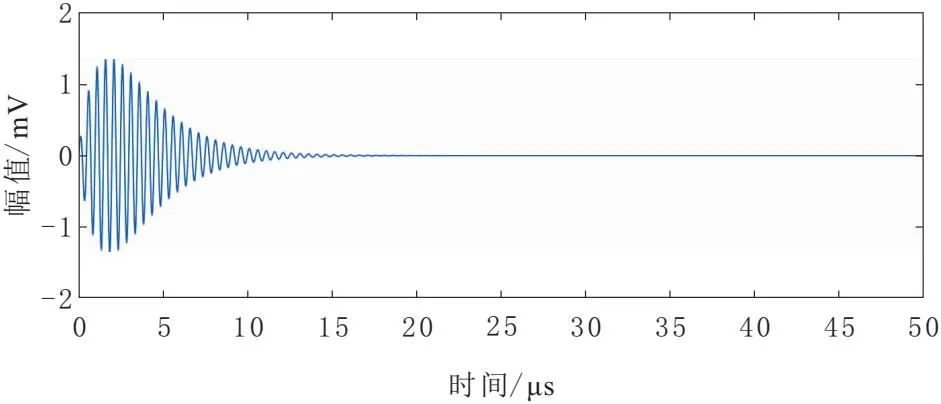
图3 局放信号波形

假设电缆C端缺陷发生局部放电,即在C端注入局放信号,在A、B两端采集到具有时间延迟的局放信号。为模拟现场环境的电磁噪声干扰,加入-5 dB的高斯白噪声。A、B端采集到的信号波形如图4所示。

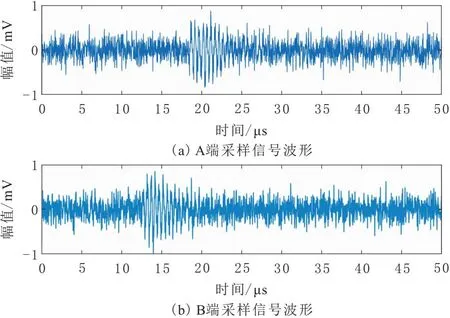
图4 双端采样信号波形

根据仿真电缆参数建立频率-波速特性曲线,如图5所示。可以看出,低频时信号波速随频率的增大显著升高;频率大于3 MHz后,波速随频率变化缓慢, 并无限接近一常数。局放电磁波具有较大的频带宽度,且其中心频率的选取受周围环境干扰噪声的影响。故本文通过顺序统计滤波器(OSF)自适应分割信号频谱,并通过峭度准则选取局放信号的相应频带,如图5,通过测量仿真信号的中心频率fz得出局放脉冲信号波速v=1.659 3×108m/s。

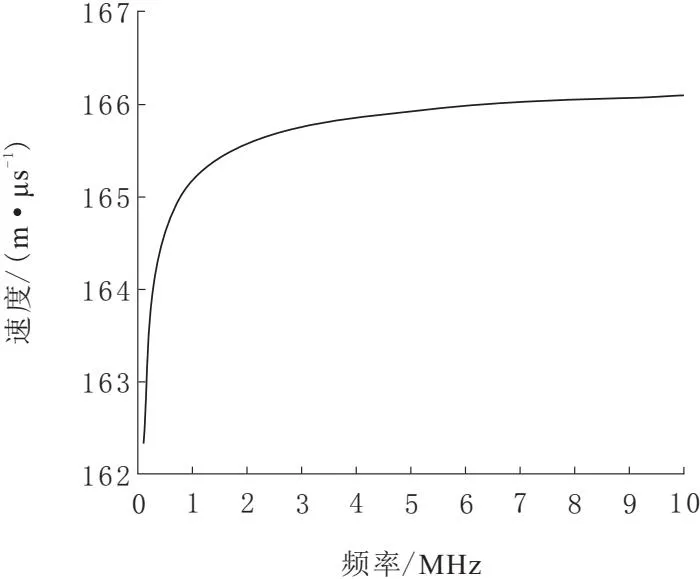
图5 电缆频率-波速特性曲线

2.2 仿真结果与讨论

为综合分析本文方法的精确性与鲁棒性,考虑在不同缺陷点位置、不同信噪比、不同采样频率条件下对局放信号进行定位,并将定位结果与峰值法、能量法、直接相关时延估计(CC)法进行对比,上述3种定位方法采用经验波速v0=1.67×108m/s,本文方法采用波速频率特性估计波速v=1.659 3×108m/s。

2.2.1 局放源位置对定位精度的影响

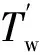
表3 不同局放源位置的定位结果

由表3可知,本文方法总体定位精度优于传统时延估计定位法。将图6的局放源位置-定位误差曲线分成2个阶段,在阶段1,随着缺陷点逐渐靠近电缆端部,4种方法的定位误差都急剧增大;在阶段2,当缺陷点越靠近电缆中心,4种方法的定位误差越小。如图7所示,当局放源靠近电缆近端A点时,电缆远端B点收到的第1个局放信号xb1(t)与经A点反射的第2个局放信号xb2(t)重叠,导致峰值法、能量法和CC法都出现了不同程度的时延估计误差。

图6 不同方法的定位结果

图7 局放信号入射波与反射波传播

本文提出的优化脉冲时窗技术,可以精确识别入射波xb1(t)和反射波xb2(t),将反射波剔除于相关函数运算之外,有效提高了时延估计精度。此外,本文提出的定位方法采用修剪均值滤波技术,通过对定位结果样本集进行3层数据过滤处理,最大限度地减少了由于局放源位置靠近端部造成的定位误差。即使在距离电缆端点仅25 m的情况下,也能达到5.26%的定位相对误差。在阶段2中,由表3可以看出,随着局放源越靠近电缆中心,优化脉冲时窗Tw远小于固定时窗,在减小了残余噪声干扰对定位精度影响的同时,提高了算法的性能与效率。

2.2.2 信噪比对定位精度的影响

保持局放源与电缆端点的距离为1 200 m不变,考虑信噪比为-10 dB、-5 dB、0、5 dB和10 dB情况下,比较4种局放定位方法在不同信噪比下的定位结果,如表4所示。

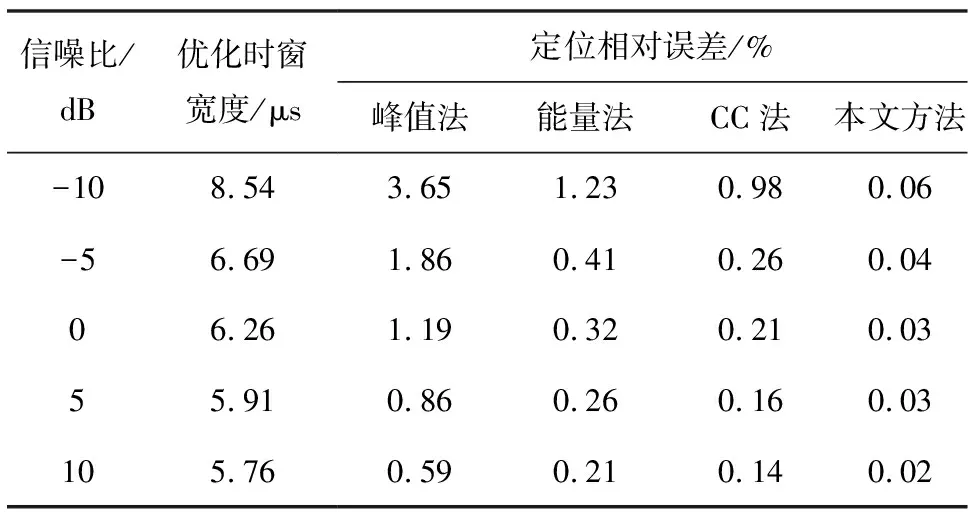
表4 不同信噪比下的定位结果

在信噪比较低(-10 dB)时,基于峰值法的定位方法,无论是从精度还是鲁棒性的角度看,较其他3种方法定位效果不佳。归其原因主要在于峰值法在低信噪比条件下的初始波峰值并不突出,再加上信号波形畸变较大,局放脉冲上升沿起始点定位困难;其次,噪声干扰会影响阈值选取,导致波峰选取出现误差。

2.2.3 采样频率对定位精度的影响

设定局放源位置和信噪比不变,当信号采样频率分别为25 MHz、50 MHz、100 MHz、200 MHz时,4种方法的定位结果如表5所示。

表5 不同采样频率下的定位结果

当采样频率较低(25 MHz)时,4种方法都出现了不同程度的定位误差。其中,峰值法的定位误差相对较大,这是由于较低的采样频率导致信号的初始波峰发生了畸变与漂移,造成波峰对应的发生时刻读取困难。能量法的问题与峰值法类似,在低采样频率的条件下累积能量曲线发生畸变,导致信号的初始时刻会出现变动。相比较而言,CC法和本文方法定位效果较好,由于CC法无需估计两端采样信号的波前到达时间和波峰发生时刻,仅依靠相关函数作用下估计信号发生的时间延迟,因此即使在较低的采样频率下也能保持较高的定位精度。与CC法相比,本文定位方法的精度更高,本文所提方法考虑了波速的频率特性,局放波速估计更加准确。此外,修剪均值滤波算法对多定位样本结果进行过滤,最大限度地减小了由于低采样频率导致的相关函数最大时延估计误差问题,因此,本文方法具有更小的定位相对误差。

3 试验验证

3.1 试验平台

为验证本文提出的局部放电在线定位方法的准确性,在某电缆厂开展了电缆局放定位试验,试验原理如图8所示。试验中所用电缆长度为90 m,电缆型号为ZR-YJV26/35 kV,具体参数如表6所示。在距离电缆A端27 m处设置一长30 mm、宽2 mm、深1 mm的沿面划痕缺陷。高频电流互感器(HFCT)钳住电缆屏蔽层的接地引线,电缆缺陷发出的局放信号被HFCT检测到,通过RG316同轴线送至局放检测仪双端口处理。

表6 ZR-YJV26/35 kV电缆结构参数

图8 局放定位试验接线

3.2 试验结果分析

本文试验的局放信号时域波形如图9所示。

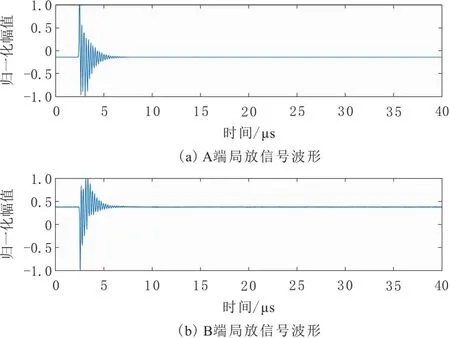
图9 试验测得的双端局放信号波形

由图9可知,实测局放信号较为分散,导致其中心频率难以确定,将局放信号利用小波分解为n个频率(记为dn),通过读取各频段的中心频率,并采用加权平均运算确定最终的信号中心频率,如表7所示。

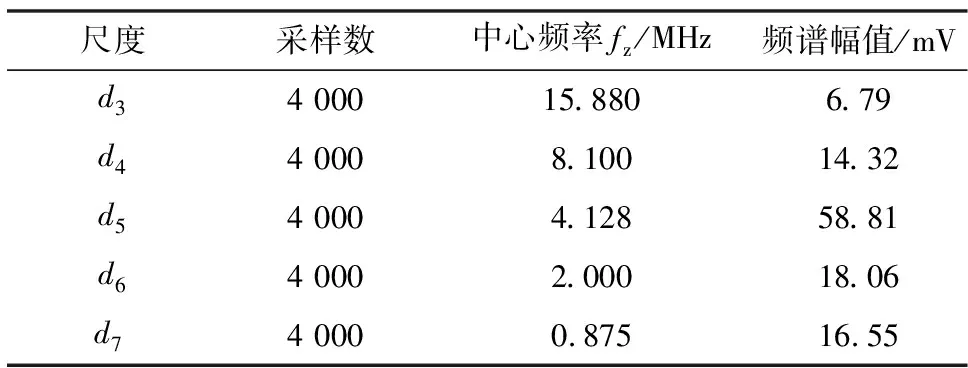
表7 实测A端信号小波分解结果

表7显示了各尺度下中心频率对应的频谱幅值,可以看出,尺度d5下的中心频率幅值最大。将各尺度下的中心频率进行加权平均,得到实测A端局放信号频谱中心频率为4.375 MHz。对B端局放信号采用相同的小波分解操作,最终得到B端局放信号频谱中心频率为4.398 MHz。根据试验电缆的基本参数,绘制相应的频率-波速特性曲线,测量得到的局放中心频率估计局放信号的频变波速为vA=1.779 1×108m/s,vB=1.779 5×108m/s。

为减小采样频率对相关函数最大时延估计的判别影响,在相关函数峰值附近选取5个采样点用于拟合峰值曲线,以获取最精确的时延估计值[15]。最终的局放试验单一样本定位结果如表8所示。

表8 单一样本定位结果

从表8中可以看出,单一样本定位结果与实际局放源位置差距较小,基本满足工程实践在线定位要求。 考虑到局放脉冲在电缆传播过程中会出现色散现象,当局放信号刚从局放源发出,此时的脉冲信号中心频率较高,随着信号传播距离的增大,脉冲信号的上升沿和下降沿变得平缓,其中心频率随之减小,即局放信号的中心频率随着信号的传播出现衰减,影响波速估计。

3.3 试验结果对比

为与其他时延估计定位法进行对比分析,采用峰值法、能量法、CC法对采样局放信号进行定位分析。4种方法均采用本文提出的修剪均值数据滤波算法进行数据处理,最终的定位结果如表9所示。

表9 不同方法定位结果对比

由表9可知,对4种方法的试验定位结果与仿真分析结果一致。峰值法、能量法和CC法均未考虑到局放波速的频率特性,造成定位结果出现误差[16]。而本文方法通过绘制试验电缆相应的频率-波速特性曲线,准确估计局放波速。此外,优化脉冲时窗技术能够根据信号信噪比和设备采样频率,自适应地调整相关函数窗口大小,最大限度地减小了相关函数出现“畸变峰”和“假峰”的概率,改善了时延估计精度。

4 结束语

本文基于经典的时延估计方法,提出一种电缆局部放电双端在线定位技术。首先在PHAT-GCC方法的基础上,提出优化脉冲时窗技术,根据局放源在电缆中的相对位置,自适应调整相关函数的时窗大小。随后在仿真及试验中对本文方法的精度进行了验证。得到的主要结论如下:

a.优化脉冲时窗技术相比于传统的固定时窗,在有效降低噪声干扰对时延估计影响的同时,能够提高算法的运算效率,更加适应局部放电在线定位的工程需求。

b.针对工程实践中异常数据多、定位误差大的问题,提出一种修剪均值数据滤波算法,通过构造3层数据过滤器对采样数据进行过滤,得到最终的定位结果。

c.对本文方法进行仿真与试验分析,结果表明,相比传统的时延估计定位方法,本文方法在环境干扰严重、检测设备采样频率受限的条件下,能够有效提高时延估计精度,减小定位误差,试验定位相对误差为0.47%,满足工程实际要求。