Negative magnetoresistance in the antiferromagnetic semimetal V1/3TaS2

Zi Wang(王子), Xin Peng(彭馨), Shengnan Zhang(张胜男), Yahui Su(苏亚慧), Shaodong Lai(赖少东),Xuan Zhou(周旋), Chunxiang Wu(吴春翔), Tingyu Zhou(周霆宇), Hangdong Wang(王杭栋),Jinhu Yang(杨金虎), Bin Chen(陈斌), Huifei Zhai(翟会飞), Quansheng Wu(吴泉生),5,Jianhua Du(杜建华),‡, Zhiwei Jiao(焦志伟),§, and Minghu Fang(方明虎),6,¶

1Department of Physics,China Jiliang University,Hangzhou 310018,China

2Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3Department of Physics,Zhejiang University,Hangzhou 310027,China

4Department of Physics,Hangzhou Normal University,Hangzhou 310036,China

5University of Chinese Academy of Sciences,Beijing 100049,China

6Collaborative Innovation Center of Advanced Microstructure,Nanjing 210093,China

Keywords: magnetoresistance,antiferromagnetic semimetal,band structure

1.Introduction

The recent discoveries of both long-range magnetic ordering in the atomically thin layers of Cr2Ge2Te6,[1]CrI3,[2]and Fe3GeTe2,[3,4]and the chiral solitons in Cr1/3NbS2[5,6]and Fe1/4TaS2[7]rekindle interest in the intercalated transition metal dichalcogenides (TMDCs).TMDCs are a class of layered materials, whose structure can be classified into 1H(triangular prismatic), 1T (octahedral), 2H (hexagonal), 3R(rhombic), and so on, depending on the local coordination of atoms around the central transition metal atoms.The intercalation(or doping)of atoms(or molecules)can modulate the physical properties of materials,[8-10]such as, the Cu intercalation in TiSe2,leads to superconductivity,[11]the Fe,Cr intercalations of TaS2or NbS2result in long-range magnetic order.[12,13]More interestingly, the Cr intercalation in NbS2leads to the chiral soliton lattice formation due to the antisymmetric Dzyaloshinskii-Moriya (DM) interactions.TMDCs become a material platform for exploring various exotic physical properties.

2.Methods

V1/3TaS2single crystals were grown by a chemical vapor transport method with two steps.First, polycrystalline samples were prepared by using a stoichiometric of V (99.9%),Ta (99.9%), and S (99.99%) powders, whose mixtures were sealed in an evacuated silica tube and heated at 1073 K for a week.Second, the evacuated silica tube containing the polycrystalline powders with iodine as transport agent(10 mg/cm3)was placed in a tube furnace, and heated for 7 days with a temperature gradient from 1223 K to 1123 K.The hexagonal crystals were obtained at the cold end, whose typical dimensions are 2 mm×1 mm×0.2 mm(see the inset of Fig.1(d)).The composition of crystals was determined by the energydispersive x-ray(EDX)technique,as shown in Fig.1(c),to be of V:Ta:S=1:3:6.The crystal structure was checked by both polycrystalline (not shown) and single crystal x-ray diffraction (XRD), as shown in Fig.1(d).The (00l) peaks with a small width at half maximum were observed, indicating that the obtained crystals have high quality.The length of thecaxis was estimated to be 11.19 °A,which is similar to that reported previously.[17]

The longitudinal and Hall resistivity and magnetization measurements were carried out on the quantum design physical property measurement system (PPMS-9T) and magnetic property measurement system (MPMS-7T), respectively.To calculate the electronic band structure, and Fermi surface of bulk V1/3TaS2, the Viennaab initiosimulation package(VASP)[18,19]with the generalized gradient approximation of Perdew, Burke, and Ernzerhof for the exchange-correlation potential[20]was employed to perform the first-principles calculations based on the density functional theory (DFT).The projector-augmented wave(PAW)potentials were adopted for the inner electrons[21]and the cores of S:(Ne,3s23p4),Ta:(Xe,6s15d4), and V:(Ar, 4s13d4) have been used in the calculations.The kinetic energy cut off was chosen as 360 eV for the wave function, and theΓ-centered mesh 6×6×4 was used to calculate the electronic structures.The tolerance of energy convergence was chosen to be 10-6eV.

Fig.1.(a)Side view of crystal structure with V atoms intercalated between the TaS2 layers.(b)Top view of crystal structure along the c-axis.(c)Energy dispersive x-ray spectrometer(EDXS)for the V1/3TaS2 crystal.(d)Single crystal XRD pattern.Inset: the photograph of a crystal.

3.Results and discussion

Figures 1(a) and 1(b) show the crystal structure of V1/3TaS2,a hexagonal non-centrosymmetric structure,where the V3+ions occupy the octahedral position and intercalate between the triangular prismatic layers of the parent 2H-TaS2,forming a superlattice ofstructure with lower symmetry.The host TaS2layer provides conduction electrons,while the orbital moment of V3+is usually quenched due to the octahedral crystal fields of neighboring S2-,and the localized moment of V3+mainly originates from the spins of the unpaired electrons.

In order to understand well the physical properties of V1/3TaS2compound, we calculate its electronic band structure.Figure 2(a)shows the band structure of the A-type AFM phase with considering spin-orbit coupling(SOC).It is clear that the Fermi energy level (EF) locates in the conduction band,indicating a metallic behavior,there are three hole pockets(the left,near theΓandApoints)and one electron pocket(near theKpoint),and the results reveal that it is antiferromagnetic out-of-plane and ferromagnetic in-plane.These results demonstrate that V1/3TaS2is a magnetic semimetal.

Fig.2.(a)The calculated band structure with SOC.(b)Temperature dependence of magnetic susceptibility,χ=M/H,measured at H=2000 Oe applied along the c-axis with both ZFC and FC processes.The right axis is for χ-1(T).

Next, we discuss the results of magnetization measurements.Figure 2(b)shows the temperature dependence of magnetic susceptibility,χ=M/H,measured at a magnetic field ofH=2000 Oe applied along thec-axis with zero-field-cooling(ZFC) and field-cooling (FC) processes.Although theχ(T)curves measured with ZFC and FC processes seem to overlap with each other,small differences at low temperatures can be recognized in the magnifiedχ(T) curves (not shown).With decreasing temperature, the susceptibility increases continuously for both processes.A sharp peak occurs atTN=6.2 K in theχ(T) curves, corresponding to an antiferromagnetic transition.The susceptibility aboveTNfollows the Curie-Weiss law

whereCis the molar Curie constant andθis the Weiss temperature.Figure 2(b) (the right axis) shows the temperature dependence of inverse susceptibility,χ-1(T), exhibiting a linear temperature dependence.We obtained thatC ≈0.11 cm3·K·mol-1, corresponding to the effective momentµeff≈2.7µB/V3+, andθ ≈3.8 K, close toTNvalue, by fitting theχ-1(T) data between 10 K-300 K.Different from the observations that two magnetic transitions emerge in the polycrystalline or as-grown V1/3TaS2single crystals,only one transition was observed in our crystals, implying our crystal has high quality(no impurities or disorders).Early,V1/3TaS2was identified as a ferromagnet by Parkinet al.,[22]similar to that suggested for other intercalated TMDCs, such as,Cr1/3TaS2, a soliton candidate;[13]Mn1/3NbS2, a ferromagnet with a long period spin modulation.[23]Recently,based on their magnetization and neutron diffraction results on a single crystal of V1/3TaS2,Luet al.[17]suggested that V1/3TaS2is an A-type antiferromagnet,composed of a staggered stacking of ferromagnetic planes,with a small out-of-plane canted(2°)ofXYspins and the Neel temperatureTN=32 K.Although theTNvalue here is different from that reported by Luet al.,[17]we believe that the magnetic structure at low temperatures is the same as that determined by their neutron diffraction and the exchange interaction analysis,i.e.,an antiferromagnetic stacking of ferromagnetic planes with a small canting of V3+spins(A-type AFM).

Fig.3.(a) Temperature dependence of longitudinal resistivity ρxx measured at zero field, the inset shows resistivity measured at various magnetic fields.(b)Field dependence of MR at various temperatures with a magnetic field applied along the c-axis.

Third,we discuss the influence of magnetic transition on electronic transport properties.Figure 3(a) presents the temperature dependence of longitudinal resistivity,ρxx(T), measured at zero field.With decreasing temperature,the resistivity decreases at first, reaches a minimum at about 60 K, then increases before dropping again belowTN.The resistivity exhibiting a maximum atTNis usually due to the scattering of local spins to the conduction electrons,which is also confirmed by the resistivity data measured at magnetic fields.As shown in the inset of Fig.3(a), with increasing magnetic field, the resistivity aroundTNis suppressed, and its maximum atTNalmost disappears.Figure 3(b) shows the magnetoresistance(MR)as a function of magnetic field measured at various temperatures,here MR is defined as

whereρ(H)andρ(0)are the resistivities measured at a magnetic fieldHapplied along thec-axis and zero-field, respectively.Below 50 K, the resistivity decreases with increasing magnetic fieldH,i.e.,exhibiting a negative magnetoresistance behavior, and MR reaches-5%, atµ0H=8 T,T=1.8 K,which can be ascribed to reducing spin scattering by the applied magnetic field.

Fig.4.(a)Field dependence of Hall resistivity,ρyx,measured at various temperatures for a V1/3TaS2 crystal.(b)Components of the conductivity tensor,i.e.,σxy as a function of magnetic field for different temperatures(＜100 K).Hollow dots represent the experimental data and the solid lines are the fitting curves using the two-carrier model.

Finally, as mentioned above, the band structure calculations demonstrate that V1/3TaS2is a magnetic semimetal,which is also confirmed by the Hall resistivity measurements.Figure 4(a)shows the Hall resistivity as a function of the magnetic field applied along thec-axis,ρyx(H,T),measured at various temperatures(1.8 K-100 K).Both the nonlinear field dependence ofρyx(H,T)below 20 K and the change in the slope ofρyx(H,T)from a positive value below 10 K to negative one above 40 K imply the existence of multi-band structure.To parameterize the Hall data,we analyze the longitudinal and Hall resistivity using a two-carrier model, as we discuss for other semimetals.[24-29]In this model,the conductivity tensor in its complex representation is given as[30]

wherene(nh) andµe(µh) denote the carrier concentrations and mobilities of electrons (holes),eis the elementary charge, respectively.To appropriately evaluate the carrier densities and mobilities, we calculate the Hall conductivityσxy=ρyx/(ρ2xx+ρ2yx) using the original experimentalρyx(H,T)data.Then,as shown in Fig.4(b),we fitσxy(H,T)data using the fitting parameters and the field dependence given by[31]

The obtainedne(nh) andµe(µh) as a function of temperature are plotted in Fig.5 and the inset.It is clear that both theneandnhare almost independent of temperature below 20 K, such asne(1.8 K) = 0.22×1019cm-3,ne(20 K)=0.34×1019cm-3,nh(1.8 K)=0.21×1019cm-3,nh(20 K)=0.54×1019cm-3,and enhance markedly with increasing temperature, such asne(100 K)=8.2×1019cm-3,nh(100 K)=3.6×1019cm-3.On the contrary, the mobility of the hole,µh, increases rapidly with decreasing temperature and is much larger than theµeat lower temperatures,although they are almost the same at higher temperatures.These behaviors are similar to those occurring in many other semimetals.[27,32]

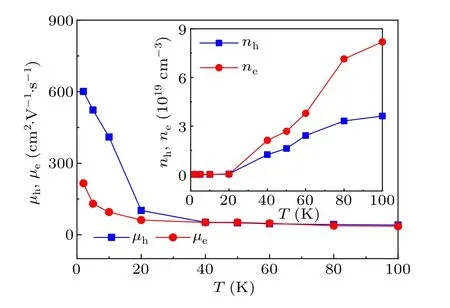
Fig.5.The carrier mobilities, µh and µe, and (inset) the carrier concentrations nh and ne, as a function of temperature, extracted from the two-carrier model analysis of σxy data.

4.Conclusion

We performed electronic structure calculations and measured the longitudinal resistivity, Hall resistivity, and susceptibility on V1/3TaS2crystals with a hexagonal noncentrosymmetric structure(space groupP6322).It was found that V1/3TaS2is an A-type antiferromagnet withTN=6.20 K,and exhibits a negative MR nearTN.Both band structure calculation and Hall resistivity measurement demonstrated it is a magnetic semimetal.

Acknowledgments

Project supported by the National Key Research and Development Program of China(Grant No.2022YFA1403202),the National Natural Science Foundation of China (Grant Nos.NSFC-12074335, 11974095, 5177115, 11974095, and 12188101), and the Natural Science Foundation of Shaanxi Province of China(Grant No.2022JM-028).