Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels

Xiao-Xiao Xie(谢笑笑), Liang-An Huo(霍良安),2,†, Ya-Fang Dong(董雅芳), and Ying-Ying Cheng(程英英)

1Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

2School of Intelligent Emergency Management,University of Shanghai for Science and Technology,Shanghai 200093,China

3School of Management,Henan University of Science and Technology,Luoyang 471023,China

Keywords: information diffusion,disease transmission,asymmetric activity levels,quarantine strength

1.Introduction

As is well known,infectious diseases shape the trajectory of human societies,often exerting more profound and comprehensive influences than wars or revolutions.Effective prevention and control of these diseases has thus become an essential and urgent priority in public health.Consequently,experts from various fields have turned their focus to dynamic disease propagation modeling.[1-3]

The study of disease transmission has a long history.Kermack and McKendrick introduced the well-known “compartment model”and derived a threshold for disease transmission that set the basis for subsequent studies on the dynamics of disease transmission.[4]Building on this,scholars have established classical mathematical models to describe disease transmission,such as susceptible-infected-recovered(SIR)model and susceptible-infected-susceptible(SIS)model.[5,6]Extensive research has been undertaken to extend these classical models, aiming to better understand the features of disease transmission.In recent years, various mathematical models have been employed to analyze various infectious diseases,leading to rapid advances in the field of global infectious disease dynamics.[7,8]At the end of the 20th century, the complex networks[9,10]have been extensively studied, providing a fresh perspective on disease transmission studies.[11]Complex network frameworks have proven valuable for description numerous real-world systems.[12-16]In recent years,many researchers have concentrated on studying infectious diseases within complex networks, yielding intriguing findings.[17-21]For example, Jagtapet al.explored the effects of different network topologies on optimal disease management strategies by using a degree-based SIR compartmental model.[22]Huang and Chen investigated disease transmission in interconnected metapopulation networks by incorporating the human mobility pattern, known as the radiation model, into movementinteraction-return models.[23]Zhuet al.proposed a generalized SIR model including infection threshold heterogeneity and neighboring resource support.[24]These studies have demonstrated that the emergence of complex networks has provided valuable reference for analyzing the infectious diseases.

The rapid advances in communication technology have made the diffusion of information easier than ever.Disease outbreaks often involve the diffusion of relevant information, including risk alerts, rumors, and fear.This type of information prompts individuals to take self-protection measures, such as social distancing and vaccinations, thereby exerting a significant influence on disease transmission.[25-31]Researchers have increasingly focused on the relationship between information and disease, and have achieved gratifying results.For instance,Funket al.investigated the influence of information on dynamic disease transmission, revealing that information can regulate the magnitude of infectious disease outbreak.[32]Granellet al.investigated the dynamic interplay between information propagation and disease spread, finding that both information and network topology can influence the critical threshold for disease transmission.[33]Some scholars have proposed a new unaware-aware-unaware-susceptibleinfected-susceptible (UAU-SIS) model that combines information awareness process and disease transmission process, revealing that information awareness can help suppress disease transmission.[34]For instance, Maet al.built a novel unaware-aware-unaware-exposed-infected-recovered(UAU-SEIR) model to investigate the effects of information diffusion caused by individuals and mass media on disease transmission.[35]Zhanget al.explored the influences of local and global information on disease transmission by analyzing a novel coupled disease-awareness propagation model called local and global information-controlled spreading.[36]These studies highlight the importance of information diffusion and its influence on disease dynamics, providing insights into effective strategies for controlling and preventing diseases.The MMCA is a stochastic process that describes the evolution of a series of random events, where the state of each event depends on the state of the previous event.Hence, the MMCA has been widely used in many fields.[37,38]Most scholars have adopted the MMCA approach to study the dynamic process of coupled information-disease transmission and have drawn some interesting conclusions.For example,Yanget al.[39]analyzed the dynamic process of disease transmission based on the MMCA approach,demonstrating that stronger heterogeneity in individual activities and smaller contact capability in the communication layer can promote inhibition.Considering the influence of information on disease transmission, Liet al.[40]established dynamic equations and derived disease outbreak thresholds by using the MMCA approach to study the dynamic mechanism and indicated that negative,local and global information can hinder the transmission of outbreaks under certain conditions.Similarly, Liet al.[41]also employed the MMCA approach to establish a dynamic process to study the coupled disease and information propagation in higher-order networks.Gaoet al.[42]proposed a nonlinear information-disease coupling model and theoretically analyzed the dynamic process of the intra-layer well-layers by using MMCA approach.The outcomes of the study showed that enhancing information communication,reducing information forgetting,and accelerating the healing process of disease can prevent diseases.These studies have further emphasized the key role of MMCA approach in studying the coupled information-disease interaction process.

Previous studies on information-disease propagation models have primarily focused on static networks, neglecting the influence of time-varying characteristics inherent to individual connections on disease transmission.In fact, both information diffusion and disease transmission are not static but change with time.[39]To capture a more realistic portrayal of disease transmission dynamics in the real world, it is essential to consider time-varying networks when building disease transmission models.Subsequently,researchers have attempted to depict the coupled information-disease propagation process within an activity-driven time-varying network.Most of scholars have explored coupled information-disease interaction models based on symmetry individual activity levels.For instance, Kotnis and Kuri established a new model to explore how individual activity levels affect disease transmission, revealing that disease propagation can be significantly suppressed by regulating the activity levels of infected individuals.[43]Fanet al.explored the dynamic process of coupled information-disease transmission by considering different activity levels of the same individuals across multiple networks, finding that an individual’s activity levels can affect disease transmission thresholds.[44]However, in reality,individuals often exhibit varying activity levels in different environments.[45,46]For instance, older individuals may be less active online, resulting in lower activity levels in the virtual information diffusion layer; however,they are frequently active in face-to-face interactions, leading to higher activity levels in the physical contact layer.Furthermore,quarantined patients are typically prohibited from physically contacting but maintain an active online.Therefore, it is important to analyze the influence of asymmetric individual activity levels on disease transmission.Moreover,most of scholars typically assumed a one-to-one mapping relationship between nodes in the network.However,during actual outbreaks,some infected individuals might withhold disease-related information from others due to panic and fear.[47]Conversely,some individuals with access to disease-related information might fail to take effective and timely preventive measures.In these cases, a clear mapping relationship between network nodes may not exist.[48]

Motivated by the discussion above,we utilize power-law distributions to characterize individual activity levels in each layer.This approach enabled us to explore the effects of asymmetric activity levels on disease transmission within timevarying multiplex networks.In this investigation,we construct a novel coupled propagation model.The upper layer of this model focuses on the diffusion of disease-related information,while the lower layer concentrates on disease transmission.Additionally, we consider the influence of partial node mapping relationships within the network on the dynamics of disease transmission.Subsequently, we analytically derive the critical thresholds for disease transmission in the model by using the MMCA.Finally, we perform MC numerical simulations to verify the accuracy of our theoretical analysis.

The remainder of this paper is organized as follows.In Section 2, we propose the UAU-susceptible-infectedquarantined-susceptible (UAU-SIQS) model to explore the dynamic interplay between information and disease propagation in time-varying multiplex networks.In Section 3,we derive the disease-outbreak threshold by using the MMCA.In Section 4,numerical simulations are performed to validate our theoretical predictions.Finally,in Section 5,some conclusions are drawn from the present study and the future perspectives are also presented.

2.Model description

The influence of information on disease transmission is largely dependent on individual behavior.Once individuals receive disease-related information, they are likely to promptly adopt effective preventive measures to reduce their risk of infection.Individual behavior is primarily influenced by activity levels, which can vary in different environments.Individuals with higher activity levels are more likely to disseminate disease-related information,but they are less likely to take protective measures.The existence of asymmetric activity levels within the same individual across different networks indicates that individuals may be highly active in the disseminating information in the virtual layer, they may not exhibit the same level of activity in the physical contact layer.Furthermore,an individual’s activity level can affect the probability of information propagation, consequently indirectly influencing the dynamic process of disease transmission.

To capture the nuances of this phenomenon, we propose a novel two-layer UAU-SIQS model as shown in Fig.1.The upper layer serves as the information diffusion layer,in which nodes exist in two states:U(unaware)andA(aware),denoted in blue and red, respectively.Individuals in stateUare unaware of disease-related information,whereas those in stateAare aware of it and have the ability to transmit it.The lower layer focuses on disease transmission and includes three states:susceptible (S), infected (I), and quarantined (Q), denoted in yellow, green, and purple, respectively.Individuals in stateSare uninfected,those in stateIare infected and can transmit the disease,and those in stateQare quarantined and cannot transmit the disease.We introduce power-law distributions to represent the influence of asymmetric activity levels on the propagation dynamics within each layer.According to the analysis, we classify the nodal states as six categories: unawaresusceptible state(US), unaware-infected state(UI), unawarequarantine state (UQ), aware-susceptible state (AS), awareinfected state (AI), and aware-quarantine state (AQ).We assume that once an individual is quarantined, they invariably become aware of disease-related information.Consequently,UQindividuals transition toAQstatus with a probability of one as indicated in the model:

The proposed model identifies five valid nodal states:US,UI,AQ,AS,andAI.This model operates under the following assumptions.

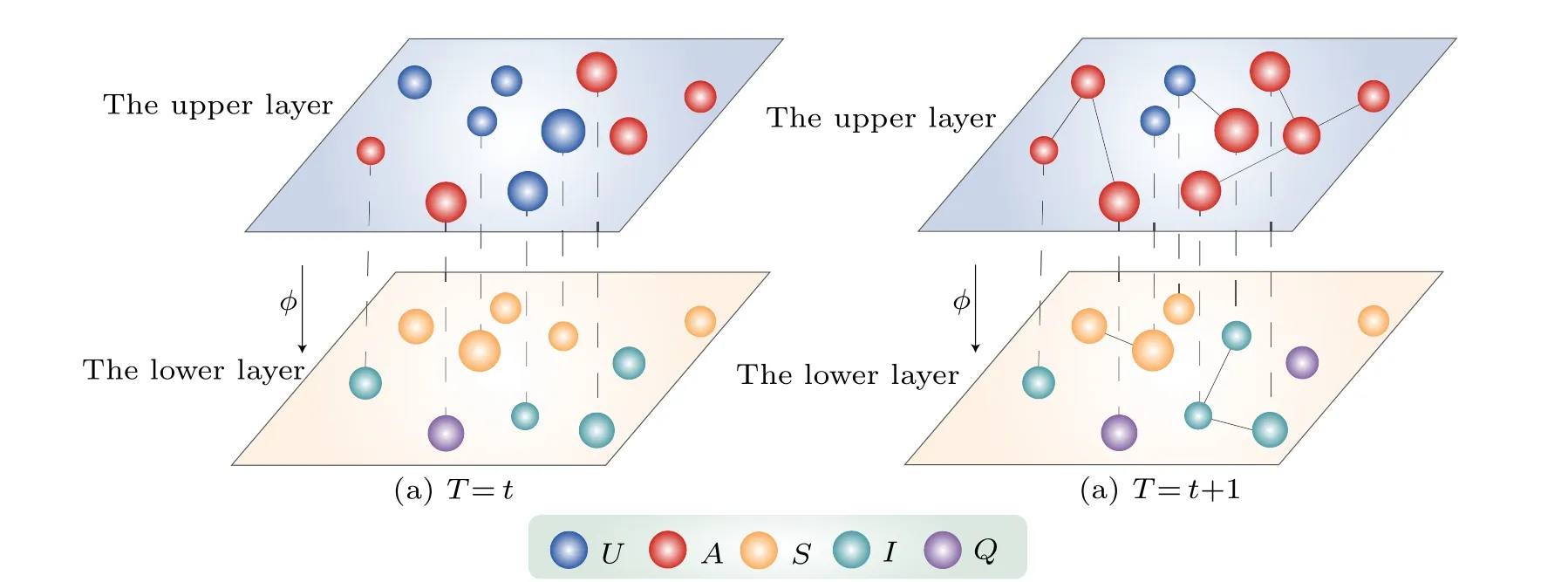
Fig.1.Schematic diagram of information-disease interaction propagation in time-varying multiplex networks.The virtual link between the upper layer and lower layer represents mapping relationship between nodes.In the network, nodes are represented by circles with varying colors indicating different states of nodes,and nodal size corresponding to their respective activity levels.

Assumption 1: Individual activity levels

Nodes have different activity levels in a two-layer network, denoting the likelihood of a node becoming activated to establish connections with other nodes at each time stept.We letai=ηvxiandbi=ηpyidenote the activity levels of individuals in the upper layer and lower layer, respectively, whereηvandηpare the rescaling factors.Additionally,xiandyiare obtained from the power-law distributionsFv(x)∝x-γv iandFv(y)∝y-γp i, respectively.Letε ≤xi ≤1 andε ≤yi ≤1,whereεis the minimum value ofxiandyi,andε=5×10-4.[49]Furthermore,γνandγpare both defined as individual activity index.Importantly,we assume that the activity levels of quarantined individuals are zero in the disease transmission layer.The network’s dynamic evolution unfolds as follows: there areNnodes in the upper layer and lower layer of the network,although they are not necessarily in oneto-one correspondence.First, in the time stept, all nodes are independent and unconnected.Second,time stept+1,nodes are activated with a probability ofai(bi) and form random connections with neighboring nodes.Notably, nodes become immediately aware of disease-related information upon infection.Subsequently, all the connections among nodes are removed.This cycle repeats until the system stabilizes.

Assumption 2:Influence of information diffusion on disease transmission

When a disease outbreak occurs, information related to the outbreak disseminates rapidly.As individuals become informed,they spontaneously adopt preventive measures,influencing the disease transmission dynamics.Consequently, the probability of an individual inS-state becoming infected can be categorized intoβUandβA.Here, the individuals inUstate andA-state get infected with probabilitiesβUandβA,respectively, whereβU=βandβA=φβU.We introduce a damping factorφ(0≤φ ≤1)to describe how information affects disease dynamics.The smaller the value ofφ,the more pronounced the influence of information diffusion on disease dynamics is.In particular,φ=0 indicates that the aware node is completely immune to the disease,andφ=1 indicates that the information has no effect on the disease.Hence,we define the probabilities as

Assumption 3: Node mapping assumption.

In this section, we specify the partial node mapping in a two-layer network framework.As shown in Fig.1, we assume that theNnodes exit in both the upper layer and lower layer.We employ the vectorL=[l1,l2,...,lN]to characterize the mapping relationships between these nodes.Specifically,li=1 andli=0 indicate the presence and absence of a mapping relationship between corresponding nodes, respectively.For instance, whenli=1, the information related to the disease disseminates immediately once aUSindividual becomes infected.On the contrary, whenli=0, individuals either remain unaware of the disease-related information or fail to take preventive measures.

Assumption 4:Influence of the activity levels of individuals on propagation rate

Most of scholars have neglected the influence of individual activity levels on propagation rate,which is a crucial factor for understanding the underlying mechanisms of disease transmission.Therefore,in this section,we focus on the influence of individual activity levels on the propagation rate to explore the dynamic process of disease transmission.The two primary aspects of this study are summarized as follows.

First,the influence of individual activity levels on the rate of disease transmission is explored.According to previous studies,[50,51]the probability of a node being infected during disease transmission depends on two key factors: the “susceptibility”of nodes and the“transmission ability”of infected nodes.We investigate the role of disease transmission by introducing the admission rate (Ei) and transmission rate (Tj).The admission rate (Ei) is the probability that a susceptible node admits infection through contacting an infected node,and characterizes“susceptibility”of nodes.We deem it to be affected by the individual’s activity level.For simplicity, we takeEi=bi.The transmission rate(Tj)is the probability that an infected node transmits disease through contacting a susceptible node, and characterizes “transmission capability” of nodes.We takeTj=β.Since the infection rate is not constant,different infection edges may have different infection rates.If we useMi jto denote the infection rate of the edge between nodeiand nodej,then according to the meaning ofEiandTj,we have

Thus,we can obtainMij=biβ.

Table 1.Definitions of key parameters.

We then investigate the influence of individual activity levels on the rate of information diffusion.we find that the information diffusion is limited by the ability of the receiver to accept the information rather than the ability of disseminator to disseminate it.We investigate the role of information diffusion by introducing the reception rate (Ri) and dissemination rate(Kj),which is a major finding of this study.The reception rate (Ri) is the probability that an unaware node receives the information through an edge connected to an aware node,depending on the activity level of the individuals.For simplicity,we adoptRi=ai.The dissemination rate(Kj)is the probability that an aware node disseminates the information through an edge connected to an unaware node in the absence of external influences.We takeKj=λ.Since the dissemination rate is not constant,different dissemination edges may have different dissemination rates.If we useHijto denote the informing rate of the edge between nodeiand nodej, then according to the meaning ofRiandKj,we have

Thus,we obtainHi j=aiλ.

To illustrate the proposed model in more detail, we outline the key parameter definitions in Table 1.

3.Analytical analysis

Understanding the outbreak thresholds for infectious diseases outbreak is essential for the prevention and control,and also for protection public health.In models of disease transmission, there exists a thresholdβcabove which the disease starts to break out (β ＞βc); otherwise, the outbreak disappears or fails to escalate.In this section,the MMCA is used to calculate this threshold for disease transmission.

Fig.2.Schematic diagram of transition probability trees for five states(US,UI,AS,AI,AQ)per time step t.

Theorem 1 Considering the topology of a two-layer multiplex network,the dynamic transmission in the lower layer is expressed by Eqs.(6)and(7).Subsequently,the threshold for disease outbreaks is expressed as

Similarly,equation(7)can be expressed as follows:

When the disease transmission stabilizes,βcis the minimum value satisfying Eq.(16), and the maximum eigenvalueΛmax(H)of the matrixHis expressed as follows:

whereΛmax(H)denotes the maximum eigenvalue of matrixH.We can observe from Eq.(21)that the value ofβcdepends on the information diffusion process,quarantine strengthτ,individual activity,damping factorsφ,and node mapping rateΛ.

4.Numerical simulations

In this section,we validate the theoretical analysis by using an extensive MC simulation experiment conducted in a Barab´asi-Albert(BA)scale-free network.The average degree of each layer in the proposed model is set to〈k〉=6.The number of nodes is set toN=1000.Based on Assumption 5: we obtain the node-mapping rateΛ=(∑i li)/N,whereli ∈L.To reduce fluctuations caused by randomness,all the simulations are run 50 times on average.We set the initial conditions of the model as follows: 10%of the nodes are infected, 10%of the nodes are quarantined, and the remaining nodes are susceptible at timet=0.Additionally,because theAQstate cannot transmit diseases, we assume that only theAIstate in the system can transmit diseases.We allow the iterative interaction dynamics to evolve in a two-layer network according to the process shown in Fig.1.We explore the influences of the damping factor, node mapping rate, node activity index, and node quarantine strength on the final disease scale by using various parameters.

4.1.Influence of information diffusion on disease transmission

First,we characterize the influence of information on disease transmission by employing a damping factorφ.As illustrated in Fig.3,we observe the proportion of infected individualsρIwith the factorsβandλin the system’s steady state and note that the value ofρIdecreases asλincreases.This phenomenon can be attributed to the fact that with higher value ofλ, information diffusion in the upper layer inhibits the scale of disease transmission in the lower layer.This trend is consistent with the observation that as individuals become more aware of disease-related information, they are more effective in curbing disease transmission.Thus, enhancing the diffusion of disease-related information is vital for disease control.By strengthening public awareness and understanding,we can better contain the disease.Furthermore,by comparing Figs.3(a)-3(c), we find that the value ofρIbecomes larger as the damping factorφincreases, while the value ofβcdecreases.This phenomenon can be attributed to the fact that a larger value ofφsuggests that information diffusion has not significantly affected disease outbreaks,and the public is more vulnerable to misinformation, which may lead people to take incorrect actions,thus facilitating the transmission of diseases.Therefore,the importance of information cannot be ignored in disease transmission control.The provision of accurate, reliable and transparent information helps the public to better understand diseases and take appropriate measures to curb their transmission.

Fig.3.Maps of ρI as a function of infection probability β and information diffusion probability λ in steady state of system.All the results of MC simulations are averages of 50 independent iterations.Different colors in panels indicate different ρI values,with darker colors indicating higher values of ρI.Parameter φ is set as follows: (a)φ =0.3,(b)φ =0.6,and(c)φ =0.9.

Fig.4.(a)Maps of ρI as a function of infection probability β and damping factor φ in steady state of system.(b) Plots of ρI versus infection probability β at different values of damping factor φ in steady state of system.All the results of the MC simulations are averages of 50 independent iterations.Different colors in panel indicate different values of ρI,with darker colors indicating larger ρI values.

We analyze the influence ofφon both the disease outbreak thresholdβcand the proportion of infected individualsρI,and the results are shown in Fig.4.From Fig.4(a),it is evident thatρIvaries with damping factorφand infection probabilityβ.Whenβ ∈[0,1]is constant,the value ofρIincreases withφ.Evidently, in the case of highφ, fewer individuals receive disease-related information, thus accelerating disease transmission.This demonstrates the critical role in enhancing public understanding of disease-related information in order to delay the outbreak.Figure 4(b) illustrates the maps ofρIas a function ofβat different damping factorsφthe steady state of system.Notably, the value ofρIbecomes larger asφincreases.In summary,during a pandemic outbreak,public health departments must disseminate timely and accurate information to ensure that the public is promptly informed.Simultaneously,they should provide scientific interpretations of disease-related information and communicate effectively with the media,experts,and other relevant departments.

4.2.Influence of mapping of partial nodes on disease transmission

Figure 5 shows the effects ofΛon disease transmission,examining varying values of the node mapping rateΛand the proportion of infected individualsρIas a function ofβandλin the steady state of system.We also consider the cases of (a)Λ=0.3, (b)Λ=0.6, and (c)Λ=0.9.Whenλ ∈[0,1]is constant,the value ofρIincreases asβincreases.However, whenΛincreases from 30% to 90%, the increasing tendency becomes less prominent.This occurs because a higher mapping rate implies that more individuals become familiar with disease-related information and take preventive measures.Consequently, the disease transmission threshold increases.Simultaneously, the value ofρIdecreases asλincreases, although this effect is not significant.For example,in the cases ofΛ=0.3 andβ=0.5,the value ofρIchanges from 0.3923 to 0.3729 whenλchanges from zero to one,and declines from 0.2864 to 0.2045 whenΛ=0.9 andβ=0.5.In addition, increasing the value ofλhas a smaller effect onρIthan changing the value ofΛ.Furthermore, the effect of increasingλonρIis smaller than that of changing the value ofΛ.For example,at different values ofλ=0.2,0.4,0.6,and 0.8,when we fix the infection rateβ=0.5(see Fig.5(a)),the values ofρIare 0.3752, 0.3719, 0.3711, and 0.3599, respectively.However,whenρIare 0.3486 and 0.2976,as shown in Figs.5(b)and 5(c),λ=0.4 andβ=0.5,respectively,showing that the increase in the mapping rate ofΛhas a greater influence on disease transmission than that inλduring an outbreak.

Fig.5.Maps of ρI with infection probability β and information diffusion probability λ in steady state of system.All results of the MC simulations are obtained as averages of 50 independent iterations.Different colors in panels indicate different values, with darker colors indicating higher values.Λ values are set as follows: (a)Λ =0.3,(b)Λ =0.6,and(c)Λ =0.9.

To provide a more intuitive representation of our experimental results, we further investigate the influence ofΛon the disease outbreak thresholdβcand the proportion of infected individualsρIas shown in Fig.6.It is evident that the value ofρIincreases withΛincreasing butturns constant in Fig.6(a).A largerΛvalue indicates a greater awareness of disease-related information among the populations,leading to increased precautions and a reduced risk of infection.Additionally,figure 6(b)illustrates the variation ofρIwith mapping rateΛand infection rateβ.We setΛ=0.3,Λ=0.5,Λ=0.7,Λ=0.9,andΛ=1,respectively.Results in Fig.6(b)are consistent with those in Fig.6(a),thereby confirming the accuracy of our results.

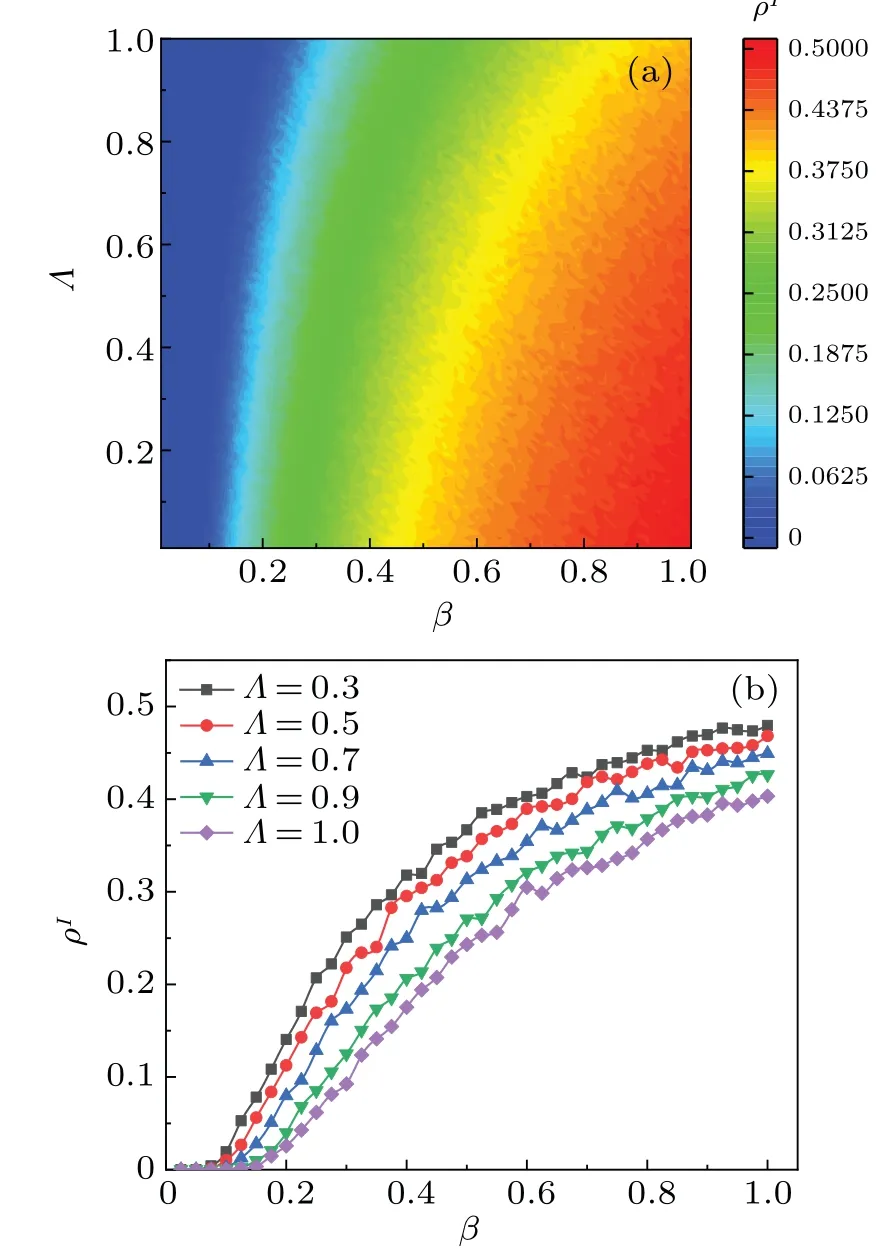
Fig.6.(a) Map of ρI as a function of infection probability β and nodal mapping rate Λ in steady state of system.(b) Plot of ρI versus infection probability β at different values of node mapping rate Λ in steady state of system.All results of the MC simulation are averages of 50 independent iterations.Different colors of the panel indicate different values,with darker colors indicating higher values.

4.3.Influence of node activity level on disease transmission

This subsection delves into the influence of node activity level on the disease outbreak thresholdβcand the proportion of infected individualsρI.Figure 7(a)illustrates the influence of upper-layer node activity level onβcandρI.Letγvtake different values.Interestingly, we find that upper-layer node activity levels have little influence on disease transmission.For instance,values ofρIare 0.6368,0.6287,0.6196,0.6070,and 0.5981, whenγvvaries from 4 to 12 withβ=0.6.This contrasts with previous study,[47]where information diffusion probability depends on the “receiving ability” of unaware individuals and the“disseminating ability”of aware individuals.In our model, enhancing the activity levels does not particularly inhibit transmission.Subsequently,figure 7(b)shows the influences of activity levels of lower layer nodes onβcandρI.Assuming thatγphas different values, we find that the changes in activity levels significantly affect bothρIandβcin the steady state of system.We observed that the activity levels of nodes in the lower layer possess a significant effect on disease transmission.For instance, the values ofρIare 0.0114,0.0620, 0.1163, 0.2448, and 0.3290 whenγpranges from 4 to 12 withβ=0.6.This phenomenon suggests that higher activity levels increases social interactions,thereby increasing the disease transmission rate.Therefore,reducing real-life activities during an outbreak,such as minimizing social outings and adhering to mask protocols,proves effective in controlling disease transmission.

Fig.7.(a)Plots of ρI versus infection probability β at different values of γv in steady state of system.(b) Plots of ρI versus infection probability β at different values of γp in steady state of system.All results of the MC simulations are averages of 50 independent iterations.

4.4.Influence of quarantine strength on disease transmission

Finally,we analyze the effects ofτ(quarantine strength)on disease transmission, and the results are shown in Fig.8.Asλincreases,ρIdecreases.This trend can be attributed to the role of disease-related information in enhancing public awareness and instigating preventive measures,thereby enhancing public awareness of the disease.We consider the cases ofτ= 0.3,τ= 0.5, andτ= 0.7 in Figs.8(a), 8(b),and 8(c), respectively.Comparisons of Figs.8(a)-8(c) show that asρIdecreases andβcincreases the quarantine strengthτincreases.This indicates the important role of quarantine strategies in disrupting transmission chains,thus lowering the disease transmission rate.Therefore, during outbreaks, quarantine measures are a vital and effective means in protecting public health, providing invaluable support for outbreak control and response measures.0 5 0 5 0 5 0 5

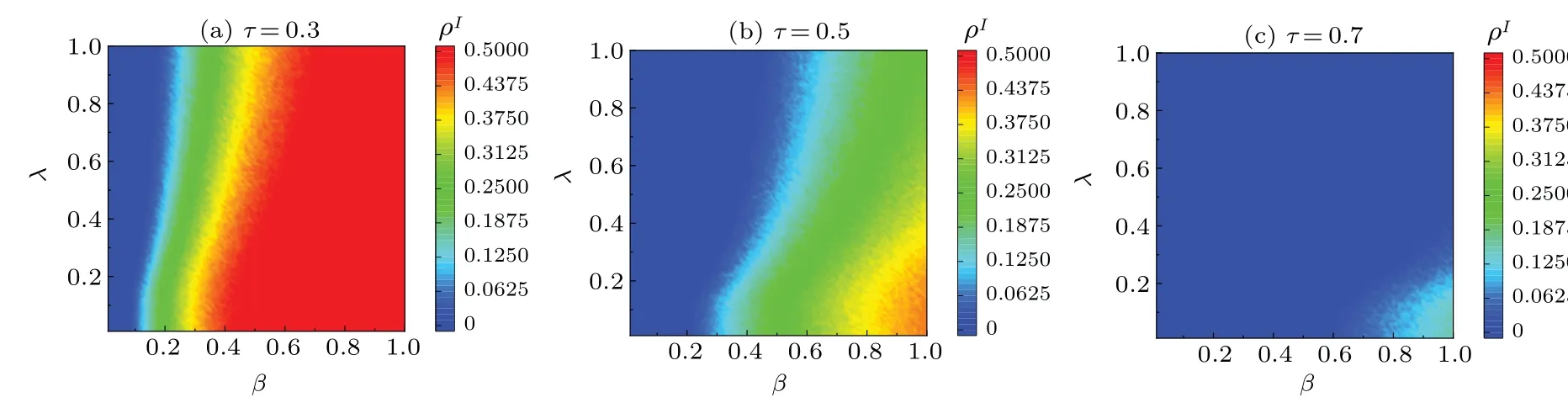
Fig.8.Maps of ρI with infection probability β and information diffusion probability λ in steady state of system.All results of the MC simulations are averages of 50 independent iterations.Different colors of the panels represent different values, with darker colors denoting higher values.Parameter τ was set as follows: (a)τ =0.3,(b)τ =0.5,and(c)τ =0.7.

5.Conclusions

In this study,we proposed a two-layer UAU-SIQS model in a time-varying network to investigate the interplay between information diffusion and disease transmission.The upper layer focuses on the diffusion of disease-related information,while the lower layer deals with the dynamics of disease transmission.We adopted power-law distributions to describe the asymmetric individual activity levels.Utilizing the MMCA,we derived the disease outbreak threshold and validated our theoretical results by using the extensive MC simulations.The key findings of this study are as follows.First, the diffusion of disease-related information reduces the outbreak threshold,enabling departments to effectively control the scale of disease transmission.Second, lifestyle modifications such as mask-wearing and minimizing outdoor activities can effectively lower the outbreak threshold.While enhancing activity levels in virtual networks can somewhat inhibit disease transmission, the influence is relatively low.Third, increasing the quarantine intensity is critical in containing and controlling the transmission of a disease.Finally,a high-mapping rate can reduce the scale of disease transmission in a two-layer network.

This study presents valuable insights into disease prevention and control.Moreover,the disease transmission dynamics are affected not only by pairwise interactions between nodes,but also by high-order interactions.Furthermore, incorporating community structure offers a more accurate description of the processes involved in disease transmission.In the future,we intend to extend our model to analyze the effects of these additional factors.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.72174121 and 71774111),the Program for Professor of Special Appointment (Eastern Scholar)at Shanghai Institutions of Higher Learning,and the Project for the Natural Science Foundation of Shanghai,China(Grant No.21ZR1444100).