基于超螺旋滑模及前馈补偿的智能车侧向运动控制

吴晓建 ，张明华 ，王爱春 ，关龙新 ，江会华 ，彭晨若

（1.南昌大学 先进制造学院，江西 南昌 330031；2.江铃汽车股份有限公司，江西 南昌 330001）

随着人工智能技术、通信技术以及自动控制技术等的快速发展，智能化已经成为汽车发展新的趋势［1-2］.智能驾驶技术是一个集环境感知、规划决策、运动控制等功能于一体的综合系统.其中，智能车辆运动过程中的侧向跟踪控制是实现车辆自动驾驶的重要一环［3-4］.然而，由于智能车辆运动过程中存在车辆参数不确定及测试场景多变，经常导致智能车辆车速在中高速时路径跟踪效果较差和车辆场景适应性较差等问题.因此，开展研究一种对车辆参数不确定和多场景测试具有强鲁棒性的车辆侧向跟踪控制算法具有重要意义.

近年来国内外学者对智能车辆的侧向跟踪控制开展了大量的理论研究和验证.吉林大学Wang 等［5］将樽海鞘群算法（Salp Swarm Algorithm，SSA）与纯跟踪算法结合，提出一种纯跟踪算法前视距离自适应方法，并设计车辆纵向速度控制器对车辆速度进行协同控制.中国农业大学Wang 等［6］提出了一种改进的Stanley 算法用于无人驾驶拖拉机的路径跟踪控制，将航向误差的积分加入到传统的Stanley算法中，并采用多种群遗传算法优化控制器参数，提高了跟踪控制的精度.武汉理工大学胡杰等［7］设计了一种带有预瞄PID 转角补偿的模糊线性二次型调节器以进行路径跟踪控制，并对模糊控制对二次型调节器的参数进行速度自适应调节.江苏大学蔡英凤等［8］设计了基于预瞄误差的PID 反馈控制和基于道路曲率的PID 前馈-反馈控制，并设计了可拓优度评价方法根据车辆-道路系统状态选择合适的控制器.重庆理工大学刁勤晴等［9］设计了模糊控制加双点预瞄的智能车横向跟踪控制器，对大曲率路径具有良好的控制效果.以上文献中侧向控制器都是考虑车辆运动学特性，控制器设计简便，运算量较小，但上述控制器对于不同的车辆速度、场景适应性较差，尤其在车辆关键参数不确定和车速达到中高速时，横向控制误差较大.

面对车辆运动控制的鲁棒控制问题，中山大学Li等［10］提出了一种鲁棒自适应学习路径跟踪控制方法，可以有效地处理系统不确定性、外部干扰以及执行器约束，获得良好的路径跟踪性能.昆明理工大学聂枝根等［11］设计了基于动态避障预警的侧向避障鲁棒控制策略，针对避障过程前后侧偏刚度参数不确定性，提出了考虑参数动态摄动的鲁棒控制策略，以提高智能汽车侧向避障轨迹跟踪精确性.因滑模算法具有在系统状态轨迹到达滑模模态后与对象参数和扰动无关［12-13］、算法原理简单和算法运算量小等优点，也被广泛运用在车辆运动控制鲁棒性研究领域.大连理工大学李琳辉等［14］将基于视觉预瞄的车辆运动学确定的横向误差与航向误差融合成综合偏差，作为滑模切换函数的参数来设计滑模面，同时利用模糊算法减弱方向盘的抖振现象.吉林大学赵健等［15］设计了一种基于自适应动态滑模的纵向巡航控制方法，有效地消除了参数不确定和外部干扰的影响.Ao 等［16］利用超螺旋滑模算法（Super-Twisting Sliding Mode，STSM）设计了横向控制器，对规划路径进行跟踪控制，并提出了一种评价机制对超螺旋滑模、传统滑模、模型预测控制和Stanley算法进行量化评价，但超螺旋算法未考虑系统不确定性.Hu等［17］将超螺旋滑模算法用于四轮转向车辆的车道保持功能，提高了故障转弯条件下车辆保持控制的瞬态性能.以上文献均对基于滑模算法的车辆运动控制进行了探索和创新，但对于二阶超螺旋滑模对传统滑模抖振现象的改善以及滑模算法对于车辆参数不确定和驾驶场景多变对车辆横向控制影响的鲁棒性控制较少.

面对车辆参数不确定及多变场景下的鲁棒控制问题，本文提出了基于二阶超螺旋滑模与误差补偿方法相结合的智能车辆横向控制算法以提高车辆横向控制精度.最后，在Carsim-Simulink 联合仿真环境及实车试验中验证了算法的有效性和准确性.

1 车-路耦合动力学建模

1.1 车辆二自由度模型

智能车辆路径精确跟踪控制通常认为需要依托精确的车辆动力学模型，然而，匹配被控车辆的非线性车辆动力学系统精确建模具有难度，尤其是在考虑强非线性特性的轮胎模型时.图1 包含车辆横摆和侧向运动的二自由度模型，由于具有高效计算及容易匹配被控对象的特点而被广泛使用.本文采用线性二自由度操稳性动力学模型，但考虑到二自由度模型存在因模型简化及线性化而带来的不确定性，将采用超螺旋滑模算法提高控制系统的鲁棒性.

图1 二自由度车辆动力学模型及误差模型Fig.1 2-DOF vehicle dynamics model and error model

二自由度操稳性动力学模型为：

式中，m为整车质量，Iz表示车辆绕z轴的转动惯量，Lf和Lr分别为车辆质心到车辆前轴、后轴的距离，Cf和Cr分别为车辆前轴和后轴的侧偏刚度，为车辆的航向角，vx为车辆的纵向速度，δf为车辆前轮转角.

1.2 侧向控制误差模型分析

如图1 所示，定义车辆质心坐标为O（xact，yact），参考路径上距离车辆质心点O欧氏距离最近点为P（xref，yref），由此可以得出质心点O与参考路径跟踪点P的y方向误差ey为：

基于车辆横向动力学模型的滑模控制器的目的就是通过输入合适的方向盘转角，使误差ey趋近于零，使车辆准确地到达目标位置及目标航向.

2 路径跟踪控制器设计

2.1 超螺旋滑模控制器设计

针对智能车辆运动过程中存在参数不确定及道路曲率变化干扰问题，利用滑模算法，在系统到达滑模面后与控制对象参数及扰动无关的特性可得到较好改善；同时，针对传统滑模算法在参考路径跟踪控制过程中可能出现的抖振现象，二阶超螺旋滑模算法则可有效减小抖振，提高路径跟踪精度［18-19］.因此，本文采用二阶超螺旋滑模算法，以综合提高面对参数不确定时的鲁棒性及路径跟踪控制的精度.含不确定性的控制系统如式（6）所示.

式中：x∈Rn，为状态向量；f(t，x)和h(t，x)为连续函数；u(t)为系统控制输入；ξ+(t，x)为不确定误差.选择与传统滑模算法相同的滑模面s，由车辆二自由度模型及侧向控制误差模型可知滑模面s的相对阶为一阶，对滑模面s进行微分处理可得

式中：ξ1(t，s)为系统未建模误差；ξ2(t，s)为系统外部扰动.令ξ(t，s)为系统外部扰动及系统未建模动态的总误差，式（7）可改写为

到达超螺旋控制器的滑动模态时，输出u（t）可以表示为：

其中，α和β为正数，且需满足

式中，ξ(t，s)为系统外部扰动及系统未建模动态总误差，

可以看出，式（9）中出现了两个开关函数，但是这两个开关函数并不会影响系统的二阶滑模特性.在输入项u1中，开关函数sign（s）前面有一个系数|s|τ（τ∈[0，0.5]），在系统运动到滑模面附近时s≈0，因此该项的阶跃部分可忽略不计.在输入项u2中，由于开关函数被隐藏在其一阶导数内，出现在滑模面一阶导数中的是经过积分的开关项，不存在阶跃成分.在滑模面上可以保证连续的

根据车辆侧向控制误差模型，在设计超螺旋滑模控制时选择如下滑模变量s.

由于滑模变量s的相对阶数为1，将式（12）与 式（7）进行对比后可得：

得到到达超螺旋滑模控制器滑动模态时的控制输出δst.

由于控制系统的初始状态往往并不处于滑模状态，需要对系统的控制输入加入等效控制δeq，促使系统到达超螺旋控制器的滑动模态，δeq的值由得到.

因此，采用超螺旋滑模控制器的智能车辆跟踪参考路径的前轮转角输入δ为：

式中，误差ξ将采用前馈控制予以补偿.作为对比，本文也同时构建了一阶滑模路径跟踪控制器.

2.2 传统一阶滑模控制算法

传统一阶滑模控制算法控制器的设计过程步骤与超螺旋滑模算法控制器相似，首先定义滑模控制器滑模面s为：

式中，滑模面系数λ为正数.对上式进行求微分可得到

由式（19）可知，控制输入δf显式出现在中，所以系统的相对阶为1，适用于传统滑模算法及超螺旋滑模算法的运用.传统滑模算法的控制输入由等效输入δeq和开关函数δsw两部分组成，其中等效控制δeq输入目的是使系统到达滑模面，δeq=δf，由计算得到；δsw为开关函数输入，是一个不连续的输入.

传统滑模控制的总控制输入δ表示为：

其中，δeq和δsw的表达式如式（21）所示.

式中，α1为正数，调节α1的大小可以改变系统的收敛时间，需要选定一个合适的α1使系统的前轮转角输入抖振与系统的控制误差达到一个平衡.

2.3 带扰动的超螺旋算法稳定性证明

考虑智能车辆系统的未建模动态及外部干扰，在系统的输入δ中加入扰动误差.

式中：ξ(t)为系统未建模动态误差及外部干扰的 总和.令新向量γ=[γ1γ2]，其中γ1=ey，由式（23）可得

为了证明设计控制器的闭环稳定性，对选定的滑模面进行一阶微分：

将计算得出的式（22）及式（24）代入式（25）可得：

利用反步法对系统的闭环稳定性进行证明，设置新向量η=[η1η2]，其中η1=s，+ξ(t)，可将式（26）表示为：

定义状态变量[κ1κ2]T=[|s|0.5sign(η1)η2]T，式（27）可改写为：

式中：σ(t)表示一个边界函数，满足0 ＜σ(t) ＜ξ+，将式（29）代入式（27）可得

由反步法可推：假如状态空间变量[κ1κ2]在有限时间内趋于零，则状态空间变量[η1η2]也会在有限时间内趋近于零.

为证明状态空间变量[κ1κ2]在有限时间内收敛，选用如下Lyapunov条件函数.

因为λ1＞0，特征矩阵P为正定矩阵，Lyapunov条件函数V1(κ)为正定函数.对条件函数V1(κ)进行一阶微分可得：

由于0 ＜σ(t) ＜ξ+，并结合式（28）及式（29），可得：

其中，χ=χT，χ矩阵具体参数如下：

令β=0.5λ2α，χ矩阵可表示为：

当χ矩阵为正定矩阵时，可得出α的取值范围为：

由Lyapunov 第二稳定性判据可知，当α、β满足取值条件时，V1(κ) ＞0，系统具有收敛性和稳定性.

2.4 超螺旋滑模控制器误差补偿

智能车路径跟踪控制过程中需要面对车辆参数摄动、车辆运动场景多变等干扰.考虑到这些复杂的非线性和不确定因素，采用前馈控制作为误差补偿控制能更好的保证车辆横向控制效果.

基于二自由度模型横摆稳态响应特性的前馈补偿控制由车辆二自由度微分方程式（38）可以推出.

式中：Cf、Cr分别表示前后轴轮胎侧偏刚度；lf、lr分别表示前后轴距；β1表示质心侧偏角；ωr表示横摆角速度；vx表示纵向速度；vy表示侧向速度；Iz表示车辆绕z轴的转动惯量；δcp表示前轮转角.

汽车处于稳态时横摆角速度ωr为定值，此时由此可得：

由式（39）联立后消去vy后可得横摆稳态角速度增益为：

又因ωr=vxρ，其中ρ表示参考轨迹点的曲率，代入式（40）后可以得到前馈控制误差补偿量δcp，将δcp作为系统误差补偿ξ代入总输入δ.误差补偿量δcp的值为：

3 仿真分析

Carsim-Simulink 联合仿真由于Carsim 中高逼真车辆模型以及Simulink 软件中可编程、模块化等特点被广泛用于车辆运动控制算法仿真分析.仿真平台联合仿真测试中选用Carsim 软件中E 级车辆，车辆主要参数如表1所示.

表1 仿真测试车辆参数Tab.1 vehicle parameters for simulation test

3.1 多场景路径跟踪精度分析

智能车辆需要在不同工况下运行，因此在智能车辆运动控制算法开发过程中，对不同场景的适应性极为重要.本文将对图2 所示三种仿真场景仿真进行测试，验证设计算法的有效性及鲁棒性.

图2 仿真测试场景Fig.2 Simulation test scenario

对于传统滑模算法及超螺旋滑模算法分别进行三个仿真测试场景测试.仿真测试中算法参数λ值取4，α1值取0.002，α值取0.007，β值取0.001.场景一避障工况仿真测试中，仿真车辆初始位置与参考路径重合，测试车速取30 km/h 和60 km/h，测试场景路面附着系数均为0.85.图3～图6为仿真场景一避障工况的测试结果.

图3 车速30 km/h时场景一避障工况路径跟踪横向误差Fig.3 Path tracking lateral error in scene 1 obstacle avoidance condition at the speed of 30 km/h

图4 车速30 km/h时场景一避障工况路径跟踪航向误差Fig.4 Path tracking heading error in scene 1 obstacle avoidance condition at the speed of 30 km/h

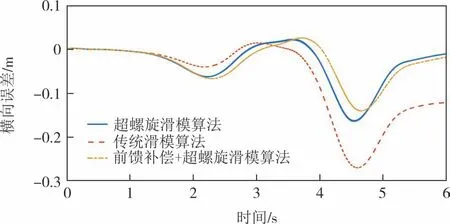
图5 车速60 km/h时场景一避障工况路径跟踪横向误差Fig.5 Path tracking lateral error in scene 1 obstacle avoidance condition at the speed of 60 km/h

图6 车速60 km/h时场景一避障工况路径跟踪航向误差Fig.6 Path tracking heading error in scene 1 obstacle avoidance condition at the speed of 60 km/h

由图3～图6仿真测试结果可知，在车速为30 km/h时，超螺旋滑模算法和传统滑模算法最大横向误差分别为0.061 m 和0.092 m，加入前馈补偿的超螺旋滑模算法最大横向误差为0.05 m，最大航向误差都保持在0.06 rad以内；当车速达到60 km/h时，超螺旋滑模算法最大横向误差和航向误差分别为0.165 m和0.025 rad，传统滑模算法最大横向误差和航向误差分别为0.271 m 和0.029 rad.当车速为60 km/h 时在超螺旋滑模算法加入前馈补偿后，最大横向误差和航向误差分别为0.142 m和0.024 rad.

场景二双移线仿真测试中，仿真车辆初始位置距参考轨迹横向偏差为0.1 m，车辆测试速度取30 km/h和60 km/h.图7～图10为仿真场景二的测试结果.

图7 车速30 km/h时场景二双移线路径跟踪横向误差Fig.7 Lateral error of path tracking in scenario 2 and doubleshift condition at the speed of 30 km/h

图8 车速30 km/h时场景二双移线路径跟踪航向误差Fig.8 Heading error of path tracking in scenario 2 double-lane change condition at the speed of 30 km/h

图9 车速60 km/h时场景二双移线路径跟踪横向误差Fig.9 Lateral error of path tracking in scenario 2 double-lane change condition at the speed of 60 km/h

图10 车速60 km/h时场景二双移线路径跟踪航向误差Fig.10 Heading error of path tracking in scenario 2 double-lane change condition at the speed of 60 km/h

由图7～图10 仿真测试结果可知，当车速为 30 km/h 时，超螺旋算法及传统滑模算法横向误差都能由初始误差0.1 m 快速收敛到0，但超螺旋算法具有更快的收敛速度.在30 km/h 时，超螺旋滑模算法及传统滑模算法的最大横向误差分别为0.064 m 和0.08 m，加入前馈补偿的超螺旋滑模算法最大横向误差为0.034 m，最大航向误差都保持在0.04 rad 以内.当车速为60 km/h 时，超螺旋滑模算法除初始横向误差0.1 m 外最大误差为0.042 m，传统滑模算法的最大横向误差为0.049 m，超螺旋滑模算法平均横向误差小于传统滑模算法；两种算法航向误差均保持在0.02 rad 之内.当车速为60 km/h时，在超螺旋滑模算法加入前馈补偿后，最大横向误差和航向误差分别为0.038 m和0.015 rad.

由图11 仿真测试车辆前轮转角输入结果可知，传统滑模算法在转弯和直行时都发生了较严重的抖振现象，车辆在转弯处时，传统滑模算法前轮转角抖振最大幅值为0.25°，超螺旋滑模算法前轮转角抖振最大幅值为0.126°，超螺旋滑模算法发生抖振现象明显小于传统滑模算法.

图11 测试场景二双移线车辆前轮转角抖振情况Fig.11 Front wheel Angle jitter in double line-shifting condition

场景三正弦函数工况仿真测试中，仿真车辆初始位置与初始航向均与参考轨迹重合，车辆测试速度取30 km/h和60 km/h.图12～图15为仿真场景三正弦函数工况的测试结果.

图12 车速30 km/h时场景三正弦函数路径跟踪横向误差Fig.12 Lateral error of path tracking in scene 3 sine function condition at the speed of 30 km/h

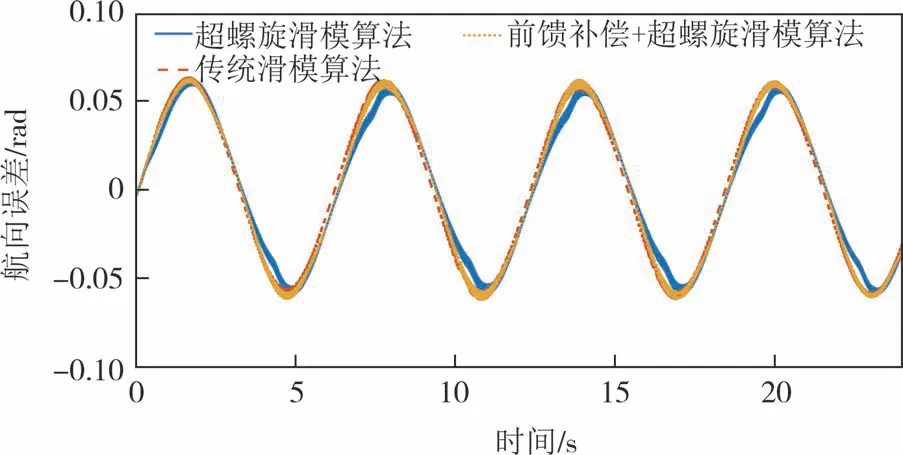
图13 车速30 km/h时场景三正弦函数路径跟踪航向误差Fig.13 Heading error of path tracking in scene 3 sine function condition at the speed of 30 km/h

图14 车速60 km/h时场景三正弦函数路径跟踪横向误差Fig.14 Lateral error of path tracking in scene 3 sine function condition at the speed of 60 km/h

图15 车速60 km/h时场景三正弦函数路径跟踪航向误差Fig.15 Heading error of path tracking in scene 3 sine function condition at the speed of 60 km/h

由图12～图15 仿真测试结果可知，当车速为 30 km/h 时，超螺旋滑模算法和传统滑模算法的最大横向误差分别为0.077 m 和0.088 m；加入前馈补偿的超螺旋滑模算法最大横向误差为0.05 m，最大航向误差基本重合，均保持在0.064 rad以内.当车速保持在60 km/h 时，超螺旋滑模算法和传统滑模算法最大横向误差分别为0.184 m 和0.256 m，最大航向误差均保持在0.036 rad 以内.当车速为60 km/h 时，在超螺旋滑模算法加入前馈补偿后，最大横向误差和航向误差分别为0.157 m 和0.025 rad，优于不加入前馈补偿时的超螺旋滑模算法.

3.2 控制算法鲁棒性分析

由于滑模控制在系统到达滑模面后，控制作用将保证系统沿滑模面到达系统原点，系统的特性和参数只取决于设计的滑模面，与外界干扰无关［20-21］.面对智能汽车运动过程中车辆参数不确定及外界干扰等情况，滑模算法具有良好的鲁棒性.对于本文算法中被控的二自由度车辆模型，对车辆质量m及轮胎侧偏刚度Cf、Cr等参数不确定及外部添加白噪声扰动进行鲁棒性分析.仿真测试场景选择场景二双移线工况，测试车速为60 km/h，参数不确定鲁棒性分析时仿真车辆初始位置及航向都与参考轨迹重合，外部扰动鲁棒性分析时仿真车辆初始位置横向误差为0.1 m，仿真测试结果如图16和图17所示.

图16 车辆质量参数鲁棒性分析图Fig.16 Robustness analysis diagram of vehicle mass parameters

图17 车辆轮胎侧偏刚度参数鲁棒性分析图Fig.17 Robustness analysis diagram of vehicle tire lateral stiffness parameters

对于车辆质量参数不确定时鲁棒性问题，由图16 分析可得，当车辆质量为0.9m～1.1m时，两种滑模横向控制算法最大横向误差都保持在0.11 m 以内；当车辆质量为0.8m～1.2m时，两种滑模横向控制算法车辆最大横向误差保持在0.18 m 以内，其中，超螺旋滑模算法最大横向误差为0.14 m，传统滑模算法最大横向误差为0.18 m；当车辆质量为0.7m～1.3m时，两种滑模横向控制算法车辆最大横向误差保持在0.41 m 以内，其中，超螺旋滑模算法最大横向误差为0.36 m，传统滑模算法最大横向误差为0.41 m.

对于车轮侧偏刚度参数不确定时的鲁棒性问题，图17 表明，超螺旋滑模及传统滑模算法在车轮侧偏刚度保持在0.9Cf～1.1Cf时，最大横向误差保持在0.13 m 以内；在0.8Cf～1.2Cf时，超螺旋滑模算法最大横向误差为0.16 m，传统滑模算法最大横向误差保持在0.20 m；在0.7Cf～1.3Cf时，超螺旋滑模算法最大横向误差为0.23 m，传统滑模算法最大横向误差保持在0.31 m.

对于系统面对外部噪声扰动的鲁棒性问题，在控制输入中加入噪声干扰.由图18 分析可得，两种滑模算法在控制输入加入白噪声干扰后都具有良好的鲁棒性，超螺旋滑模算法及传统滑模算法横向误差在加入白噪声干扰后与未加入干扰时都基本无变化.

图18 外部扰动鲁棒性分析图Fig.18 External disturbance robustness analysis diagram

4 实车试验

以某品牌车辆为实车实验平台.该测试车辆自动驾驶系统架构主要有车载工控机计算单元、环境感知模块、高精地图、RTK 定位模块、决策规划模块、控制模块及汽油车线控底盘.无人驾驶汽车实验平台中，环境感知模块结合高精度地图通过摄像头、超声波雷达等传感器获取障碍物信息实现有效避撞；RTK 定位模块获取车辆实时定位信息以确保规划和控制的精度达到厘米级；决策规划模块实时规划稳定连续的轨迹以确保跟踪控制的稳健性；控制模块计算最优控制量精准控制智能汽车运动行驶；计算单元包含一台高效算力的车载工控机，各个模块并行计算，通过机器人操作系统实现模块间信息的高效交互.

需要说明的是，因试验车目前主要用于泊车规划及跟踪控制算法开发，底盘做了7 km/h 的速度上限设置，故本文将进行低速工况路径跟踪算法测试.

如图19所示，为保证实车测试过程中的安全性，测试场景选择在某封闭园区空旷广场，测试车速为7 km/h.测试路径如图19 中红色箭头所示，为直线-圆弧的不连续曲率路径，测试曲率不连续干扰情况下控制算法的鲁棒性.实车测试过程中，由于车辆各模块之间存在通信延迟及执行机构延迟等，在滑模算法中加入动态预瞄机制［22］减少时延带来的误差影响.

图19 自动驾驶车辆测试场景Fig 19 Autonomous vehicle test scenario

自动驾驶平台硬件配置如图20所示.

图20 自动驾驶平台硬件配置Fig.20 Automatic driving platform hardware configuration

如图21～图23 所示，在实车测试过程中，运用加入前馈补偿的超螺旋滑模算法进行侧向控制的车辆最大横向误差为0.326 m，最大航向误差为0.178 rad，均为车辆进行大曲率转弯时出现；而传统滑模算法在进行大曲率转弯时横向及航向误差都大于加入前馈补偿的超螺旋滑模算法.车辆初始启动时，车辆存在初始横向及航向误差，之后车辆进行直线行驶时，横向误差快速收敛，均保持在0.10 m 以内.图24 为车辆实车运动中的车辆方向盘转角值，可以发现图中经过超螺旋控制算法计算出来的方向盘转角无明显抖动出现.

图21 实车测试中车辆的横向误差Fig.21 Lateral error of vehicle in real vehicle test

图22 实车测试中车辆的航向误差Fig.22 Heading error of vehicle in real vehicle test

图23 参考路径与实车路径对比图Fig.23 Comparison diagram of reference path and real vehicle path

图24 超螺旋算法实车测试中车辆方向盘转角Fig.24 Steering wheel Angle in real vehicle test

5 结论

针对控制模型参数不确定及干扰影响，提出了一种加入前馈误差补偿的超螺旋滑模算法用于无人驾驶车辆侧向控制，提高了无人驾驶车辆的跟踪控制精度和鲁棒性.

在三种不同场景进行30 km/h 和60 km/h 仿真测试，结果表明加入误差补偿前馈控制的超螺旋滑模算法的路径跟踪精度比传统滑模控制算法更优，且超螺旋滑模算法相较于传统滑模算法明显改善了输入量的抖振现象；同时，对于车辆质量及轮胎侧偏刚度等关键参数不确定时，超螺旋滑模算法比传统滑模算法具有更高的鲁棒性.在实车试验中，加入误差补偿前馈控制的超螺旋滑模算法运用到于低速自动驾驶车辆的横向运动控制，经过直线-圆弧曲率不连续干扰场景的测试，验证了所提出的前馈补偿超螺旋算法具有良好的路径跟踪精度.