并行相移同轴数字全息偏振成像方法

张光炜, 孟浩然, 桂 甸, 杨 昊, 刘欣悦

(1.中国科学院长春光学精密机械与物理研究所,长春 130000; 2.中国科学院大学,北京 100000)

0 引言

数字全息技术是计算光学领域的一门新兴成像技术。数字图像传感器的出现使全息术向数字全息技术发展[1-2]。随后数字全息技术被应用于相位测量[3],并出现了通过加入相移器件实现全息的相移全息术[4]。基于偏振像素掩膜的同步相移数字全息技术具有光学调试简单与大范围消色差相移等优势[5]。偏振相机的出现解决了偏振像素掩膜同步相移数字全息技术关键的核心器件问题[6]。目前并行相移同轴数字全息系统在许多领域,尤其是微生物观测领域有重要的应用[7-9]。

并行相移同轴数字全息系统使用偏振光束干涉。偏振描述光的电场分量的振动情况,是光的一种重要物理特性[10]。光在通过物体时其偏振性质会发生变化,由于物体粗糙程度、材料性质、外表纹理和观测角度的不同,会产生不同的偏振特性[11]。然而,在现有的并行相移数字全息模型中,物光被简化为完全线偏振光,理想模型未考虑物体对偏振光的调制,导致物光信息未被完全利用。针对这一问题,本文提出了一种考虑物光偏振态的四步相移数字全息系统模型,用于得到更多维度的信息。该模型考虑了干涉的偏振条件,建立了同轴数字全息四步相移系统的偏振修正模型。更进一步地,由于数字全息系统所测量的振幅与相位信息可以拓展到偏振成像所测量的偏振信息,利用偏振信息对物体实现成像。通过测量光的偏振状态并反演物体的表面信息对物体成像的成像方式称为偏振成像[12]。偏振成像在光强的空间分布信息的基础上增加了偏振度、偏振角、偏振椭率等偏振的信息[13],在军事观测[14-16]、医疗检测[17-18]、水下探测[19-21]等领域有广泛应用。将偏振与全息相结合,有利于开展对小体积、低成本、易调试的光学系统的研究[22]。

本文提出考虑偏振的并行相移同轴数字全息修正模型,该模型考虑了物体对物光的偏振调制。在该模型的基础上,本文提出了并行相移同轴数字全息偏振成像方法,通过两束不同偏振态的参考光分别与物光干涉,使用偏振图像传感器采集全息图像,反演物光在两个正交方向上的振幅相位信息,最后使用衍射角谱法重建物光复振幅,从而实现偏振成像。基于数字全息的偏振成像系统在医学、生物检测等方面有广阔的应用前景,同时有利于数字全息中孪生像的去除的研究,并可能通过偏振成像的方式实现基于数字全息的三维成像。

1 理想并行相移同轴数字全息模型

图1为传统同轴并行四步相移数字全息偏振成像系统结构图。

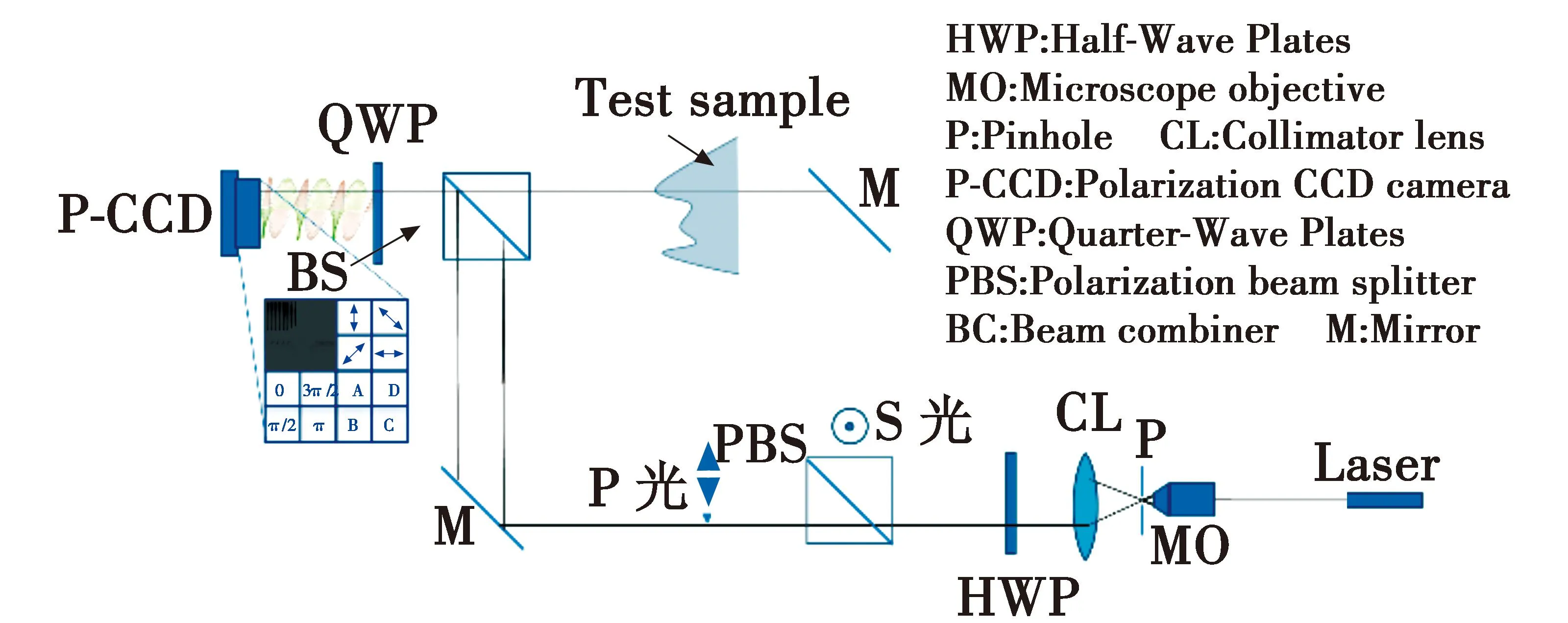
图1 传统同轴并行四步相移数字全息偏振成像系统结构

本文采用马赫曾德同轴全息光路结构实现双光束干涉,该系统具有结构紧凑、调试简单、系统稳定等优点[23]。光源为激光器输出的线偏振光,光束经过空间滤波器滤波扩束后,通过1/2波片。光束经偏振分光棱镜反射出S线偏振光,同时透射出P线偏振光。P线偏振光用作参考光,S线偏振光用作目标照明光。旋转偏振片P可以实现光强的连续调节,旋转1/2波片的线偏振方向可以改变PBS分出的物光和参考光的强度比。在参考光路放置1/4波片,可改变参考光的偏振态。物光波与参考光波经衍射传播后,通过合束棱镜合成。调节合束棱镜BS的角度,可以使物光与参考光近似同轴。物光和参考光在靶面产生干涉,并被采集生成全息图。

物光O(x,y)和参考光R(x,y)分别为水平和垂直方向的线偏振光,其复振幅分别表示为AOexp(jφO)和ARexp(jφR),通过波片后为左旋和右旋圆偏振光。干涉光束通过偏振片产生αk的相移,相移后相机靶面接收到的光强为

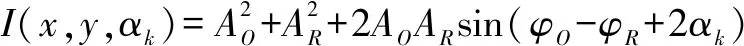
(1)

取相移αk分别为0 rad,π/4 rad,π/2 rad,3π/4 rad,代入式(1),可得到物光复振幅为

O(x,y)R*(x,y)=I(x,y,0)-I(x,y,π)+j[I(x,y,3π/2)-I(x,y,π/2)]。

(2)

采用数值计算方法进行重构得出数字全息的重构像。本文采用角谱法,算式如下

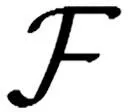
(3)

式中,H(fx,fy)为传递函数,表示为

式中:z0为重构距离;λ为激光器输出光的波长。

2 考虑偏振的并行相移同轴数字全息偏振成像模型

现有的同轴四步相移数字全息系统模型往往假设物光和参考光均为线偏振光,这些假设是为了保证经过波片调制成圆偏光在相机靶面干涉,从而利用四步相移抑制零级像与孪生像。然而在实际应用中,光在通过物体时偏振状态会产生变化。这使得物光不再是线偏振光,靶面也不再是圆偏振光束,将复杂偏振态的物光束考虑成简单线偏振光会导致信息的损失。为了获得准确的信息,需要建立考虑偏振的修正模型并优化成像方法。

理想模型将物光和参考光表示为简单线偏振光,而并未考虑物光的偏振状态变化。要对该模型进行修正,需要将复振幅用偏振光的表示方法表示。因此将物光和参考光用琼斯矩阵分别表示为

(5)

(6)

其中:Ox(x,y)和Oy(x,y)分别为物光复振幅在水平和垂直方向的投影;Rx(x,y)和Ry(x,y)分别为参考光复振幅在水平和垂直方向的投影。这种表示方法将光束的复振幅投影为两个垂直方向的复振幅分量。由于方向正交的光束不产生干涉,因此在分析偏振光的干涉现象时,可以将光束分解为水平方向和垂直方向的分量,两束水平方向的分量光和两束垂直方向的分量光分别独立产生干涉。全息图干涉过程的偏振分解如图2所示。

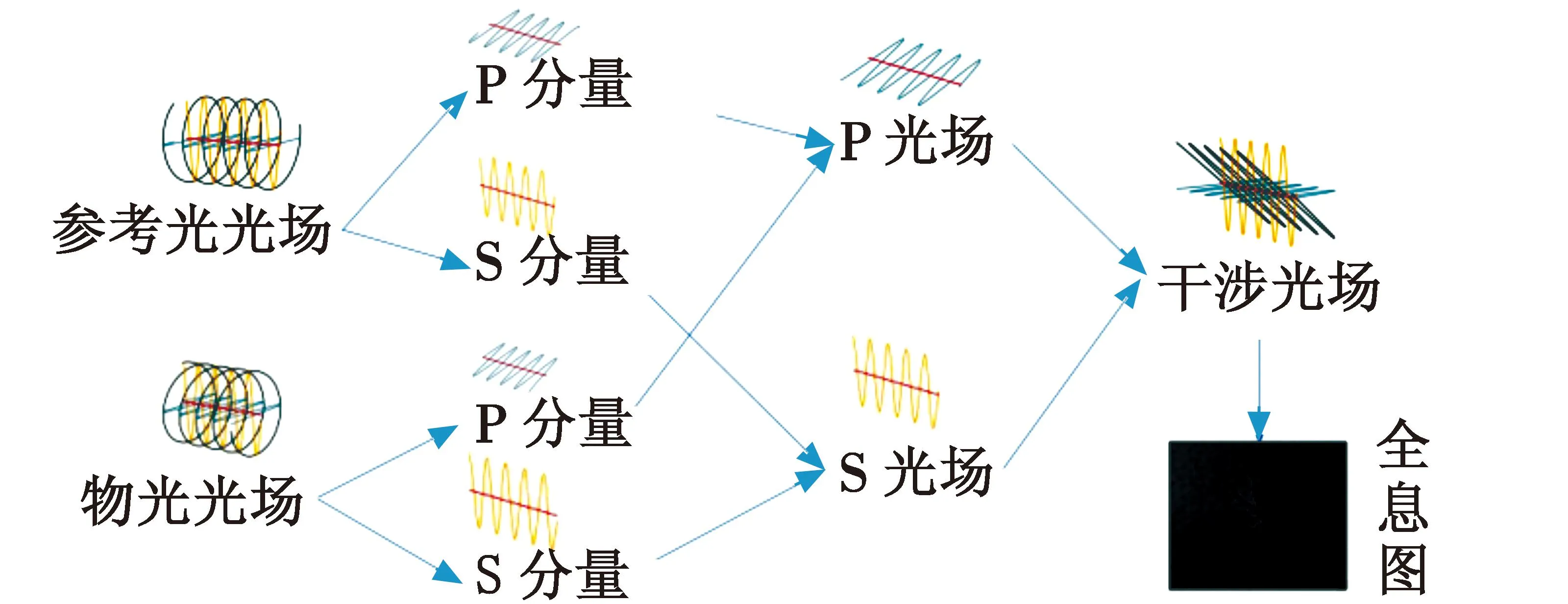
图2 全息图干涉过程的偏振分解示意图

使用偏振方向αk偏振片可以将干涉场投影。偏振片后的光强为

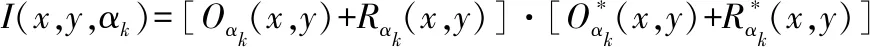
(7)

式中,Oαk(x,y)和Rαk(x,y)分别为物光和参考光在该方向的投影,其表达式为

Oαk(x,y)=Ox(x,y)cosαk+Oy(x,y)sinαk

(8)

Rαk(x,y)=Rx(x,y)cosαk+Ry(x,y)sinαk。

(9)

为验证该修正模型正确性,将偏振片偏振方向调节为水平和垂直,分别采集物光和参考光光场在垂直和水平方向的分布图像,结果如图3和图4所示。

图4 参考光场偏振分量图像

由第1章可知,理想情况下,物光与参考光分别为垂直和水平方向的线偏振光。不考虑光在传播中的偏振态变化,则物光在水平偏振方向应该没有光强分布,而只在垂直偏振方向有光强分布;同理参考光应该只在水平偏振方向上有光强分布。由实验结果可以看出参考光在垂直方向没有光强分布,即参考光为水平线偏振光,与理想模型相符;但物光在水平方向和垂直方向都存在有分量,说明目标物体对物光有偏振调制,物光不是严格垂直线偏振光。此时测量得到的相位为物光相位在垂直方向上的投影,通过获取物光在两个方向的振幅以及相位信息,可以得到更多维度的信息,实现偏振成像。

为了通过同轴数字全息四步相移系统实现偏振成像,需要利用偏振元件改变参考光偏振。假设原始参考光为一束水平线偏振参考光R0(x,y),并通过琼斯矩阵为Pi的相移偏振元件转换成其他偏振态的光,通过偏振元件前后光束的琼斯矩阵有如下关系

(10)

把式(10)代入式(9)可得

Rαk(x,y)=μi(αk)R0x(x,y)

(11)

μi(αk)=(aicosαk+cisinαk)

(12)

其中,μi(αk)为相移参数。将式(11)代入式(7)可以得到测量光强

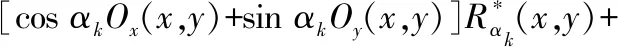
(13)

为方便计算,将式(13)写为矩阵形式

Ii(x,y,αk)=Mi,kO

(14)

式中,O为光场矩阵,表明光场复振幅信息,其表达式为

(15)

Mi,k为传输矩阵,由测量时的相移方式决定,其表达式为

(16)

测量时,首先调节参考光为水平线偏振光,采集得到多幅不同偏振方向上的全息图I1(x,y,α1),I1(x,y,α2),…,I1(x,y,αk);随后在参考光路中加入相移元件Pi,再次采集得到多幅全息图I2(x,y,α1),I2(x,y,α2),…,I2(x,y,αk),测量得到的光强与光路中光场复振幅有如下关系

I=MO

(17)

式中,I为测量矩阵,表明测量得到的光强,其表达式为

;

(18)

M由每次测量的相移矩阵组成,其表达式为

(19)

(20)

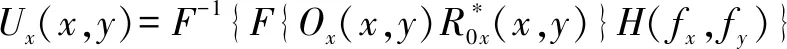
(21)

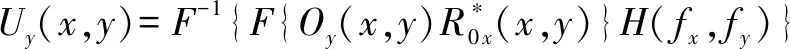
(22)

其中,Ux(x,y)和Uy(x,y)为重构所得物光复振幅的水平和垂直分量。重构完成后由复振幅可计算得到物光斯托克斯矢量,即

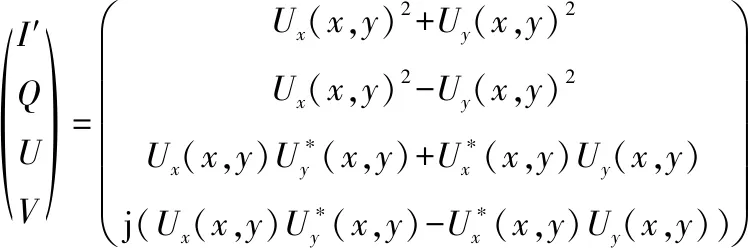
(23)

斯托克斯矢量包含I′、Q、U、V四个参量。I′为光强;Q为0°与90°方向线偏振分量;U为45°与135°方向线偏振分量;V为圆偏振分量。

3 实验与结果分析

3.1 并行相移同轴数字全息偏振成像系统的搭建

系统常用的图像探测方法有两类:1) 将工业相机作为探测器,相机前面设置一个可旋转的线偏振片,分别旋转线偏振片至对应角度对入射光进行检偏,各采集1张图像;2) 以偏振图像传感器作为探测器,通过同步相移的方法测量干涉光场不同偏振方向上的光强[24]。偏振图像传感器结构如图5所示。传感器上每个像元表面都覆盖有像素偏振片阵列,阵列上的微偏振器可以产生4个离散偏振方向(0°,45°,90°,135°)。4个方向的微偏振器组成一个完整的探测单元,在整个像素阵列上呈现周期性排列。每个微偏振器在空间上与单个传感像素相匹配。由于分时测量易受环境扰动等影响从而降低测量精度,测量次数越多影响越大,在使用两束参考光的情况下,旋转偏振片需要在每个参考光下测量至少4个角度共8张图像,而偏振图像传感器只需2种不同参考光下的2张图像。因此本文采用偏振相机采集图像。

由于本文所提出的偏振成像方法只有相移方法不同,因此无需改变传统并行相移数字全息系统的结构,只需改变偏振元件,根据图1所示系统原理图搭建的光学实验系统如图6所示。实验所用相干光源为Thorlabs HNL020LB单模线偏振氦氖激光器,功率为2 mW,波长λ=632.8 nm,光束直径为0.63 mm;偏振图像传感器采用FLIR BFS-U3-51S5P-C,其基于SONY IMX250MZR偏振CMOS传感器,分辨率为2448像素×2048像素,像素大小为3.45 μm,通过USB3.0接口进行供电与数据传输。

图6 四步相移同轴数字全息的偏振成像实验系统

3.2 分辨率板成像结果

实验所用目标物为Thorlabs R1DS1N 1951 USAF分辨率板。测量时在参考光路放置1/4波片,旋转波片使得快轴与水平方向成0°,使用偏振相机对全息图进行采集;随后旋转波片使得快轴与水平方向成30°再次采集,共采集得到2张全息图。采用平面波参考光记录并重建全息图,重建的数值衍射传播距离与目标记录距离相等,使用角谱法重建光场,采样间隔Δx为像素大小,即Δx=3.45 μm,重建的结果为和目标物体等大的清晰再现图像。图7为分辨率板的重建结果。数值重建距离为120.30 mm。

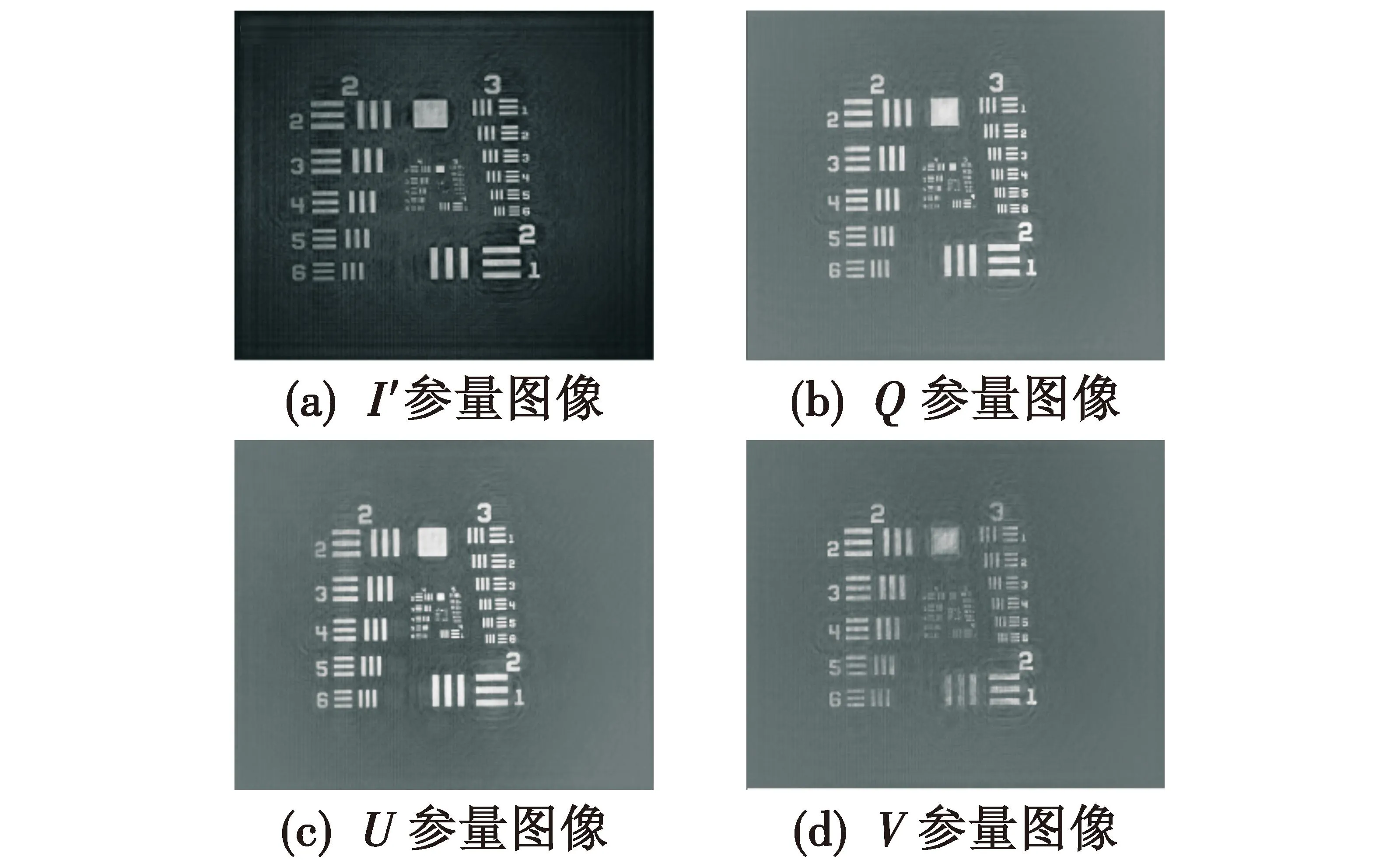
图7 偏振成像结果

重建图像可以清晰描述分辨率板的外表,说明方法不仅可以测量光束的偏振特性,也可以通过该方法测得到偏振特性描述目标物体的外形特征,实现基于数字全息系统的偏振成像。

图8所示为不同图像的分辨率分析图,由图8可见分辨率均达到了22 μm,其中I′参量可分辨6-2元素,分辨率为14 μm;Q参量可分辨5-4元素,分辨率为22 μm;U参量可分辨5-5元素,分辨率为19 μm;V参量可分辨5-4元素,分辨率为22 μm;I′参量分辨率最高,可能由于其本身亮度较高;V参量分辨率较低,可能由于产生圆偏分量较少。实验验证了并行相移同轴数字全息的修正模型的正确性,证明了通过数字全息系统实现偏振成像的可行性,为实际应用建立了基础。

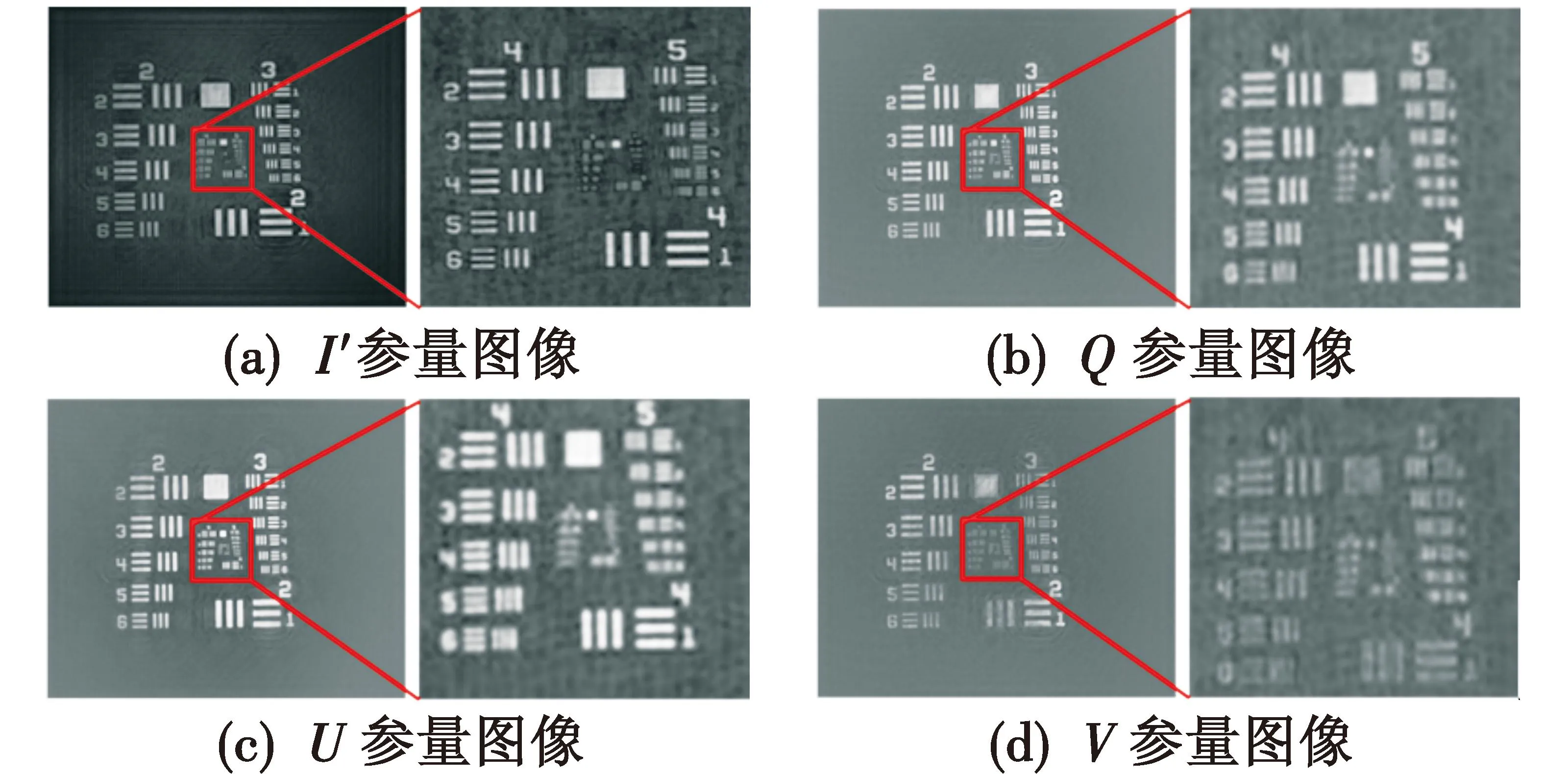
图8 偏振成像分辨率分析

3.3 测量误差评估分析

由上述成像结果可以看出,成像结果能描述目标表面形貌特征,基本实现偏振成像的功能。为进一步提高图像质量,针对系统中可能存在的误差进行分析。误差可能由如下因素引起。

1) 分时测量误差。本文介绍的成像方法需要进行分时多次测量,测量过程中环境扰动等变化可能导致测量出现误差。为研究分时测量对成像效果的影响,采用旋转偏振片为0°、45°、90°、135°采集8张图像的方式进行测量,并与上述偏振相机采集2张图像所得到的图进行对比,测量结果如图9所示。通过图像可以看出,拍摄图像张数增加时图像质量明显降低,分辨率降低至69 μm,同时图像中出现重影现象,可能是测量时光学元件的微小移动导致。

图9 采集8张图像的偏振成像结果

2) 微偏振阵列误差。由于偏振相机制造工艺问题,会导致偏振阵列消光比不一致、偏振角度与实际不符等误差。为研究偏振相机中偏振阵列误差产生的影响,对实验所用偏振传感器的透过率及偏振角度进行测量,并与理想曲线比较。测量时,使用一束均匀激光通过线偏振片对偏振相机进行照射,旋转偏振片每5°采集一张图像,计算4个不同偏振角度的灰度值I_0、I_45、I_90、I_135作为光照强度。测量得到光强随偏振角度曲线如图10所示。

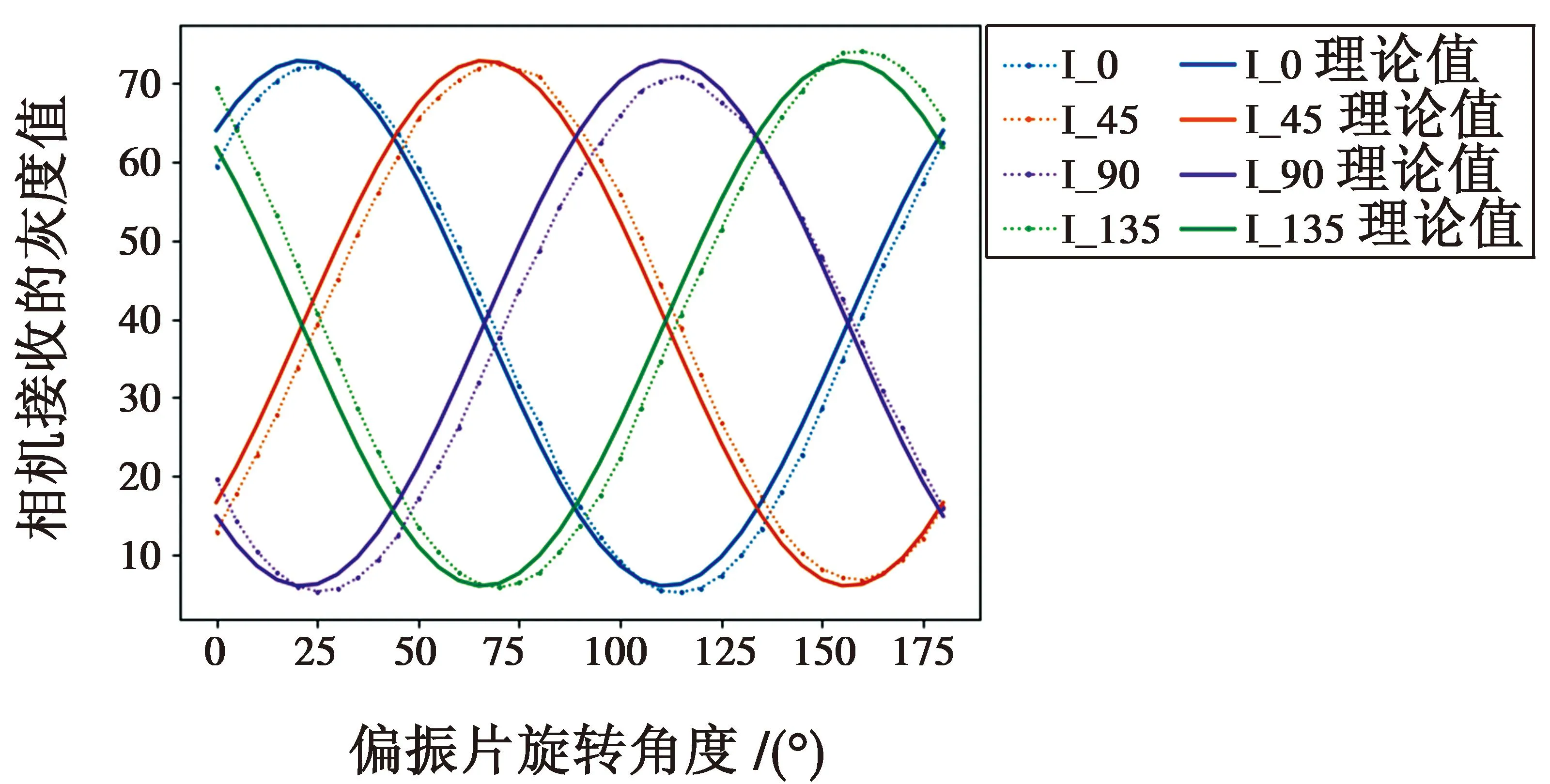
图 10 偏振图像传感器光强随角度变化测量结果

与理想角度比较,发现角度以及最大、最小光强的比值均存在误差,测量得到平均误差角度约为3.5°,平均消光比约为84∶1。偏振角度的误差以及消光比的误差将会影响算法中的参数,从而影响成像质量。

通过对误差的分析,发现不同的测量方法以及偏振相机的参数均会产生误差。若通过优化算法减少拍摄张数,并对偏振相机的误差参数进行标定,可有效提高图像分辨率,将来可以实现在微生物观测等领域的应用。

4 总结

本文开展了并行相移同轴数字全息系统的偏振成像方法的研究,提出了考虑偏振态的修正模型,依据此模型提出了并行相移同轴数字全息偏振成像方法。该方法通过物光分别与一束线偏振参考光和一束椭圆偏振参考光发生干涉,使用偏振图像传感器实现同步相移采集全息图,并使用角谱法重建得出物光在水平方向和垂直方向上复振幅分布,反演物光的斯托克斯参量,实现了偏振成像。本文验证了模型的可靠性,并搭建了使用偏振相机的数字全息偏振成像系统,实验实现了对分辨率板的斯托克斯参量成像,验证了该方法的可行性。实验表明,该方法可以对图像整体有较好的描述,实现偏振成像,完善了并行相移数字全息系统的理论模型,将系统的成像维度从相位维度扩展到偏振维度。基于数字全息的偏振成像系统有广阔的应用前景,将其应用于微生物观测等领域,可以得到微生物更多的结构及外表信息。