基于模糊PID的球形两栖机器人的设计及控制

崔雪锴, 白 越, 裴信彪

(1.中国科学院长春光学精密机械与物理研究所,长春 130000; 2.中国科学院大学,北京 100000)

0 引言

随着机器人及计算机视觉技术的不断发展,特种机器人搭载光学镜头或武器等装备进行作业的场景也越来越多,如无人机搭载相机进行地图建模、电力巡检,军用及警用无人机搭载光谱仪等设备进行侦察、扫毒等工作。但现有移动型机器人大多只能单一环境作业,常见的有无人机、无人小车等。虽然当前有部分机器人平台兼具多栖运动能力[1],但往往是无人机与小车的简单组合,结构冗余,所需运动空间较大,不能适应狭小空间下的作业,且当前无人机续航时间普遍偏短,无人机与小车的简单叠加大大增加了载具本身的自重[2-3],严重影响续航时间。针对上述问题,设计了一种可变形球形陆空两栖机器人。机器人通过变形可以实现地面球形机器人及空中四旋翼构型的自主切换,采用一个驱动电机实现模式的切换,整机质量轻、体积小、续航时间长,对其他可变形两栖机器人在结构、控制上具有一定的借鉴作用[4]。

1 球形两栖机器人结构设计

1.1 多运动模式结构设计

地面运动模式下机器人构型选择球形机器人,飞行模式构型选择四旋翼[5-6]。球形机器人相较于传统轮式、足式、履带式机器人无倾倒问题,具有较好的动态平衡性。飞行模式下四旋翼构型结构对称,利于地面运动模式下的静态稳定性。图1为机器人地面滚动模式和飞行模式的结构示意图。

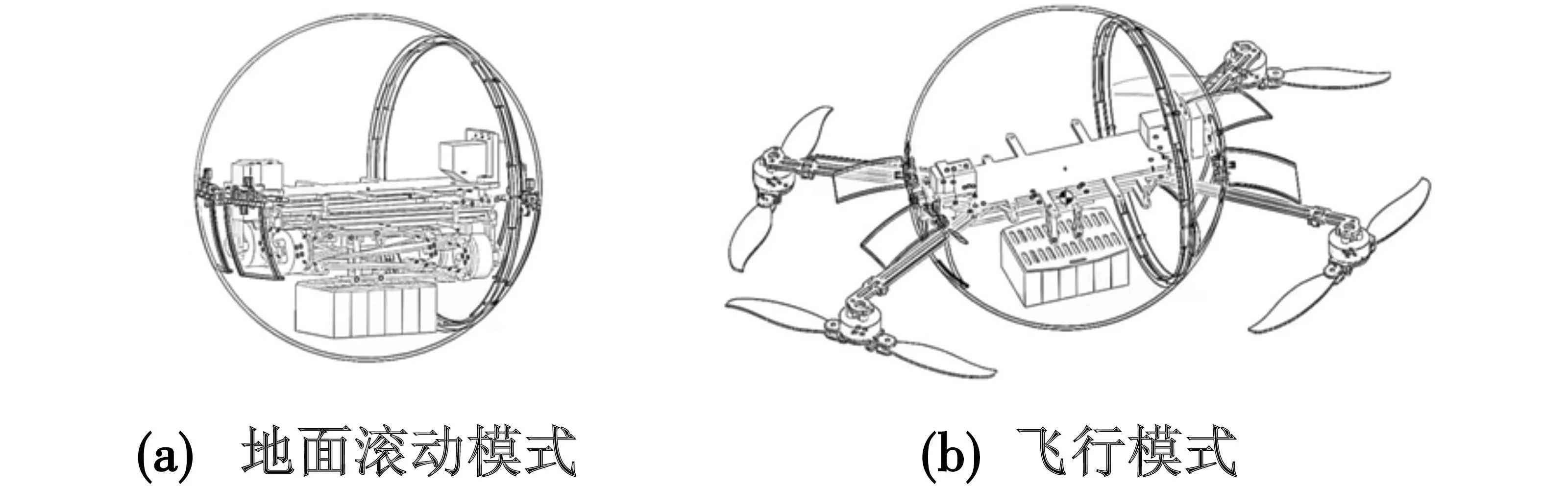
图1 球形两栖机器人结构示意图

1.2 模式切换部分结构设计

当前常见陆空两栖机器人外形尺寸都偏大,造成这个问题的主要原因为:飞行模式下多采用无刷直流电机,而无刷直流电机停转后停止位置是不固定的,因此桨叶的停止位置也是不固定的,所以必须给桨叶留出足够的旋转空间,这使得机器人外形尺寸和自重较大,影响机器人运动续航时间。针对此问题,设计了一种模式切换方式,解决桨叶停转后位置不确定的问题。

模式切换部分由两组丝杠滑块机构和收桨机构组成,如图2所示。两组丝杠滑块机构通过一对圆柱齿轮连接,每个滑块上分别连接两组电机臂,滑块带动飞行动力系统直线运动实现模式的切换。

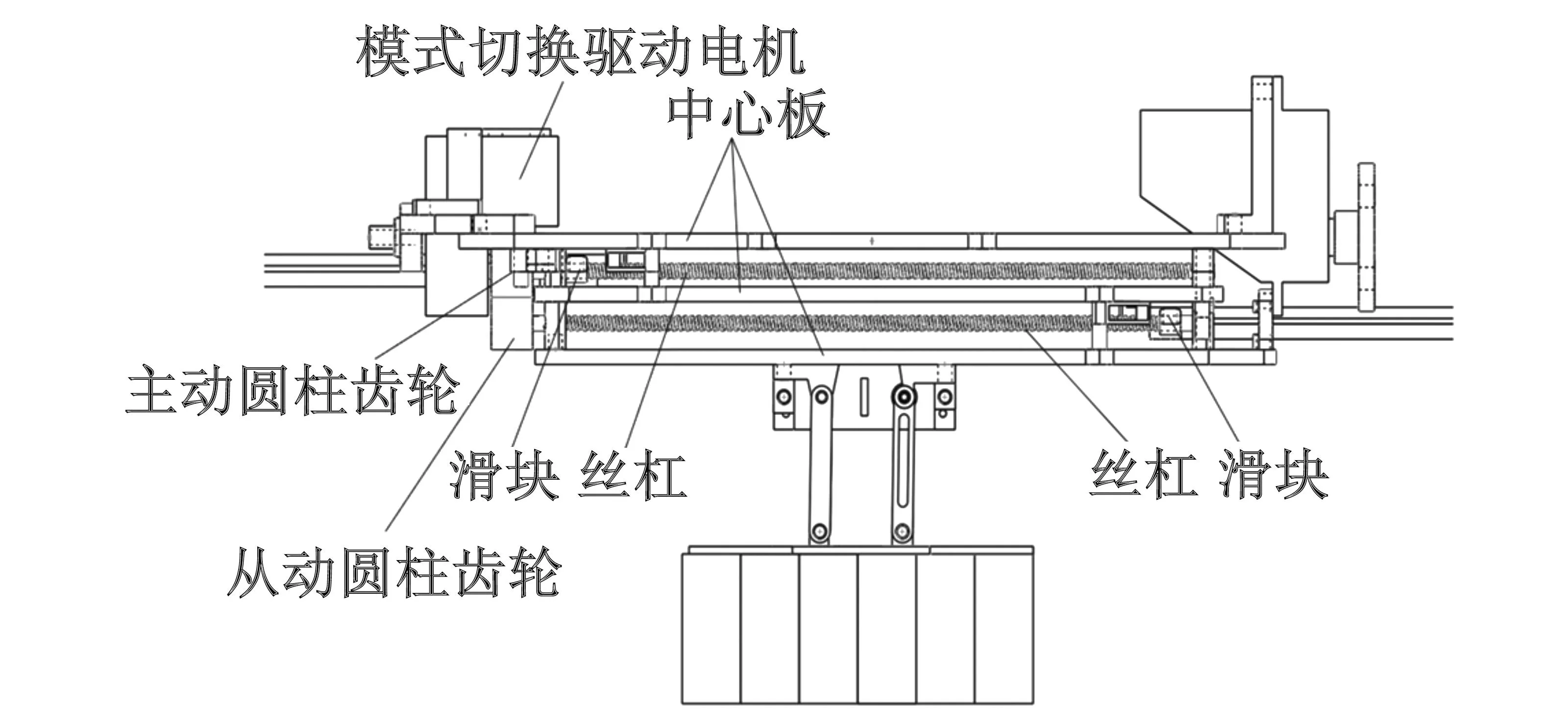
图2 模式切换整体示意图

图3为两种运动模式下的丝杠滑块机构状态示意图。

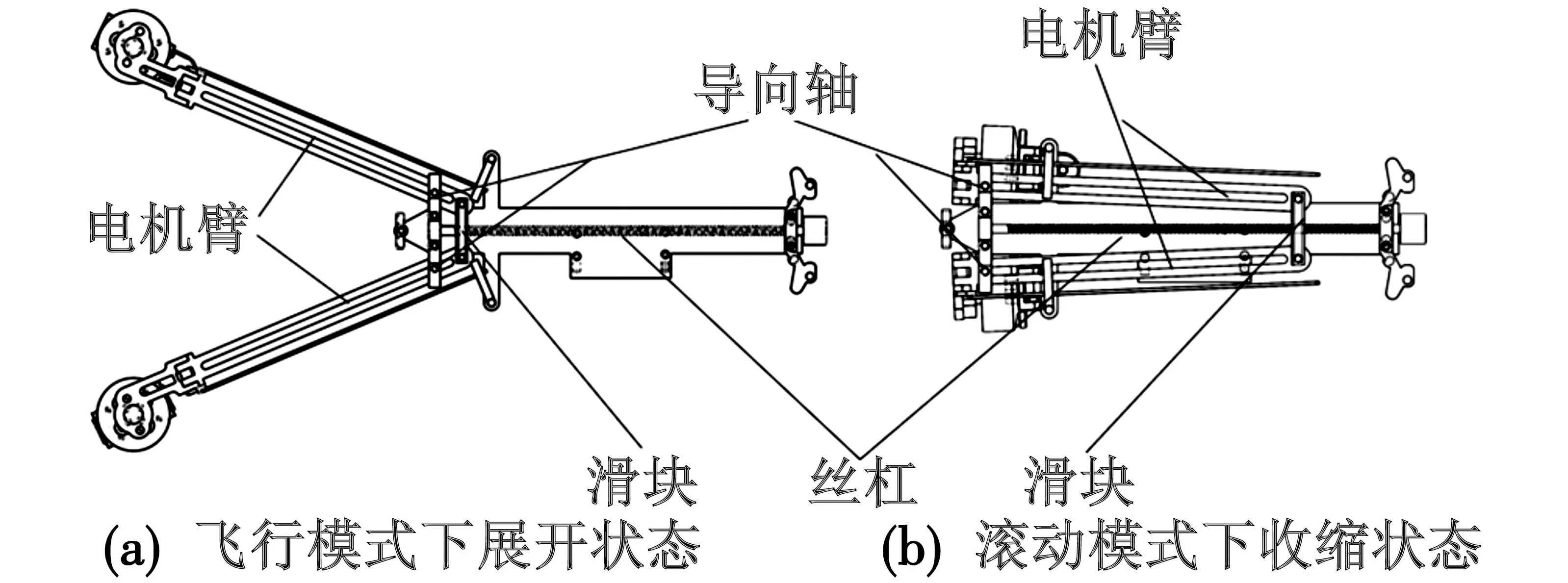
图 3 不同运动模式下状态

图4为收桨部分结构示意图,要实现载具的运动模式完全自主切换,必须解决螺旋桨停转后位置不确定的问题,通过折叠螺旋桨和折叠桨夹的方式,实现螺旋桨的回收。

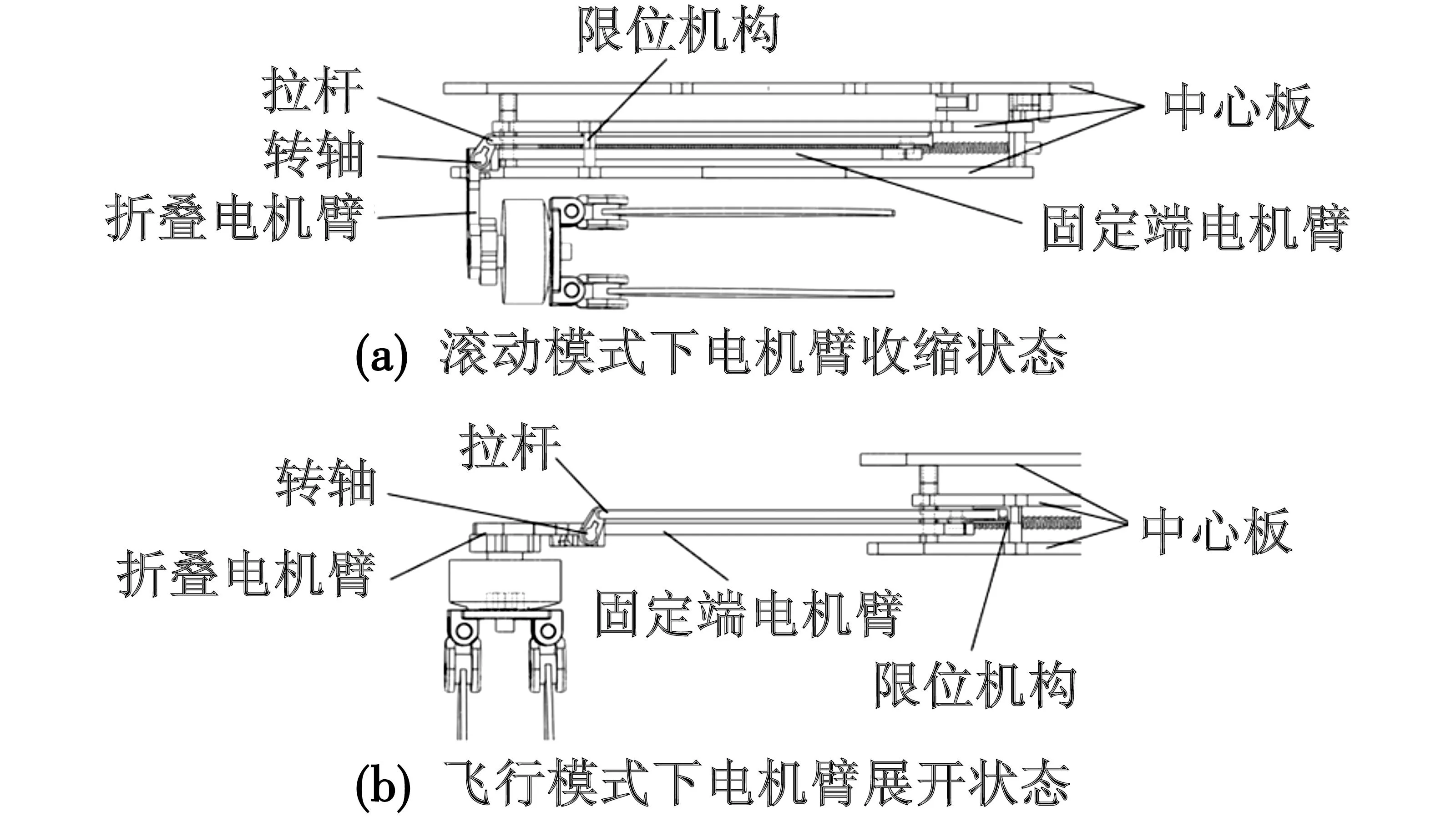
图4 收桨部分示意图

2 球形两栖机器人复合运动控制器设计

2.1 复合运动下的运动学模型

本文采用欧拉角描述载具运动时的姿态[7-9],设机体坐标系为ObXbYbZb,参考坐标系为OnXnYnZn,设偏航角为φ,俯仰角为θ,横滚角为γ,如图5所示。

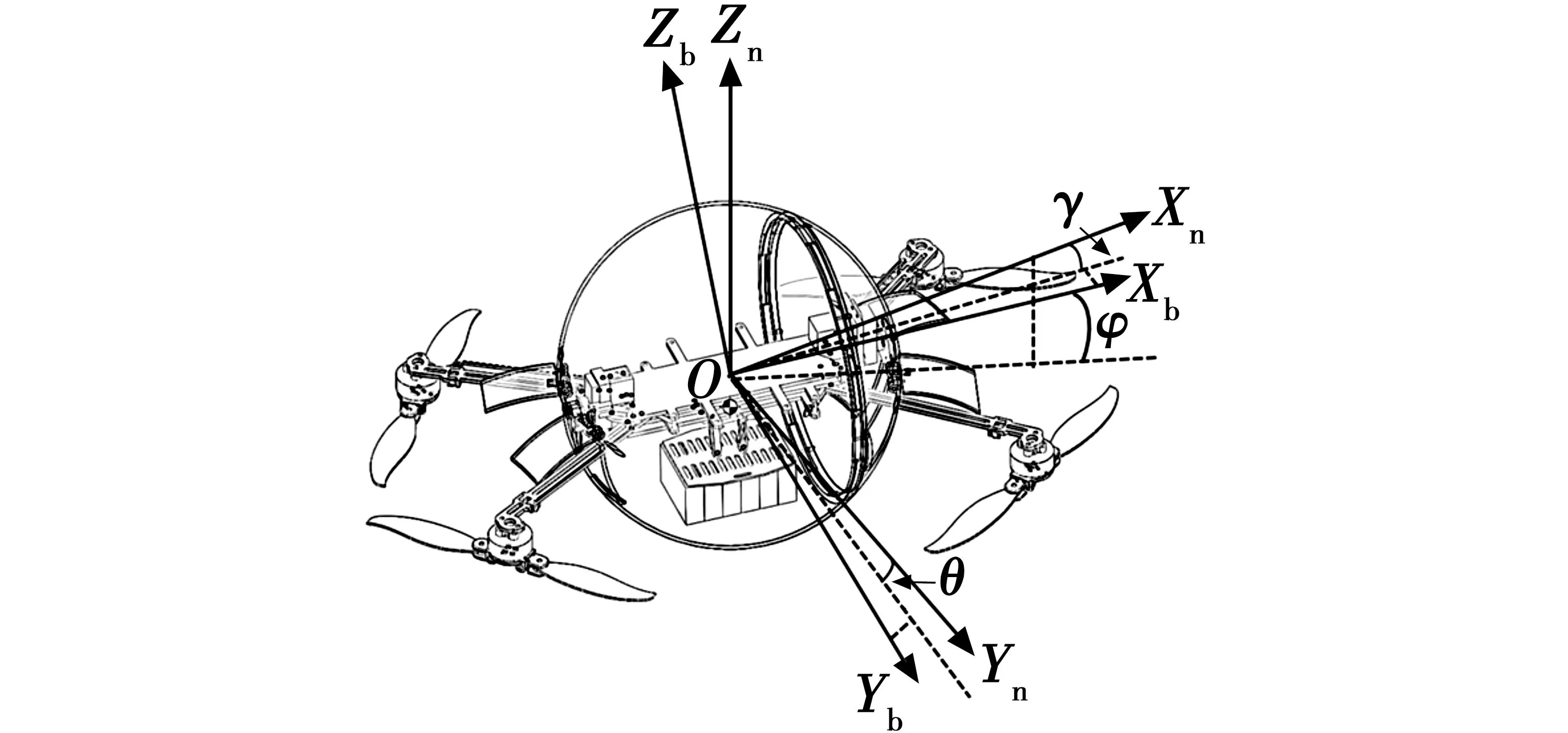
图5 坐标转换示意图

机器人在运动时的姿态变化,可以看作机体坐标系分别绕参考坐标系做3次旋转而来,因此分别讨论3次单独的旋转,得到单独旋转的坐标系,再计算得出完整的载具运动坐标转换矩阵,即

(1)

式中:

(2)

(3)

(4)

将式(2)、(3)、(4)代入式(1)可得载具完备的坐标转换矩阵为

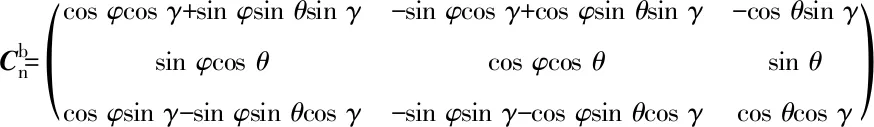
2.2 复合运动下的动力学模型

首先,建立机体坐标系ObXbYbZb及参考坐标系OnXnYnZn,根据牛顿第二定律可知

(5)

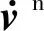
根据式(5)可得

(6)

式中,n3为参考坐标系下的单位矩阵。将单位矩阵与坐标转换矩阵代入式(6),可得飞行模式下的位置动力学模型为

(7)

M′=Ga+τ

(8)

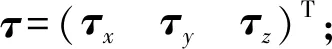
(9)

联立式(8)、式(9)可得飞行模式下的姿态动力学模型为

(10)

式中:Ω为角速度向量;I为系统绕质心转动惯量。

在滚动模式下,由于机器人没有绕Z轴方向的转矩,因此只讨论其俯仰角与横滚角的动力学模型。推导过程中各参数意义如表1所示。

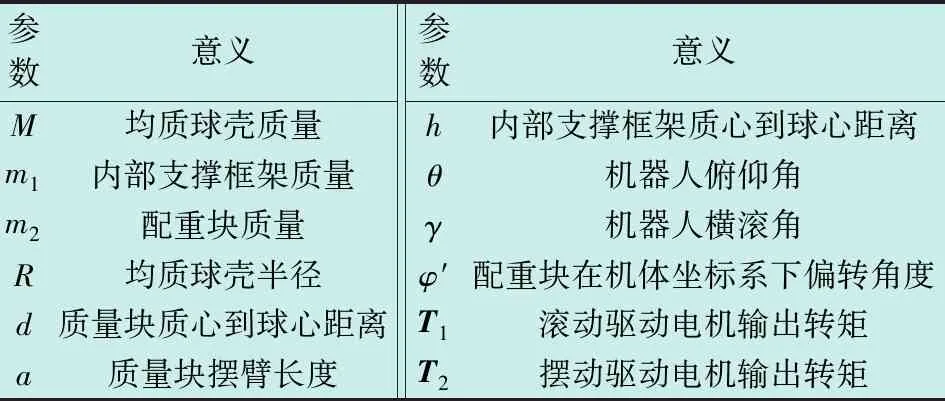
表1 各参数意义说明

根据拉格朗日方程

L=Eq1+Eq2+Eq3+Eq4-Ep

(11)

建立滚动模式下的动力学模型。式中:Eq1、Eq2、Eq3、Eq4分别为内部支撑框架动能、均质球壳动能、质量块动能、驱动单元输出轴动能;Ep为系统势能。

设S为移动距离,JM为球壳对球心的转动惯量,J1为滚动驱动电机输出轴的转动惯量,J2为质量块驱动电机输出轴的转动惯量,则有

(12)

(13)

(14)

(15)

Ep=m1g(h-hcosθ)+m2g(d-dcosφ′cosθ)。

(16)

在滚动时机器人有4个自由度,但在只考虑俯仰与横滚通道的情况下,只取2个通道,根据拉格朗日方程,欠驱动系统不完全约束时[11]有

(17)

联立式(11)～(17)可得滚动模式下姿态动力学模型为

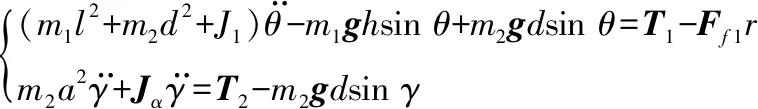
(18)

式中:Ff1为滚动驱动电机与输出轴之间损耗力;r为滚动驱动电机输出轴的半径。

2.3 复合运动控制器设计

2.3.1 基于串级PID的飞行姿态控制器

在飞行模式下,可以推导出完整的飞行动力学模型,在对比模糊PID与串级PID两种控制方法后发现,在飞行模式下模糊PID对飞行姿态提升不大。为节省处理器算力,飞行模式采用串级PID的方法:外环为角度环,采用比例控制,输入e1为期望姿态角与实际姿态角误差,输出ω为角速度;内环为角速度环,采用PID控制,输出为角加速度。则控制律为

(19)

2.3.2 基于模糊PID的滚动模式姿态控制器

根据上文的推导,机器人在地面运动模式下是一个欠驱动的不完整非线性系统,得到的动力学模型不能完全准确描述系统,因此滚动模式下姿态控制采用模糊PID的方法,通过模糊控制自整定在滚动过程中的PID参数,达到较好的控制效果。

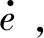
(20)

(21)

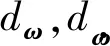
根据PID控制原理制定如下模糊规则:

1) 当姿态误差大时,需要增大Kp值,使系统快速响应,但较大的误差会导致积分项饱和,所以Ki要减小,并且Kp增大导致系统响应快,误差变化率增大,因此减小微分项,所以Kd减小;

2) 当误差中等大小时,需要减小Kp,避免产生较大超调量,为避免积分饱和此时继续取较小Ki值,但为了提高系统响应速度,此时要选取相对较大Kd值;

3) 当误差很小时,为了减小稳态误差,Ki选取较大值,同时为了减小超调量,克服振荡,选择较大Kd值。

模糊规则如表2～4所示,表中,NB、NM、NS、ZO、PS、PM、PB代表模糊子集论域对应的模糊输入、输出。

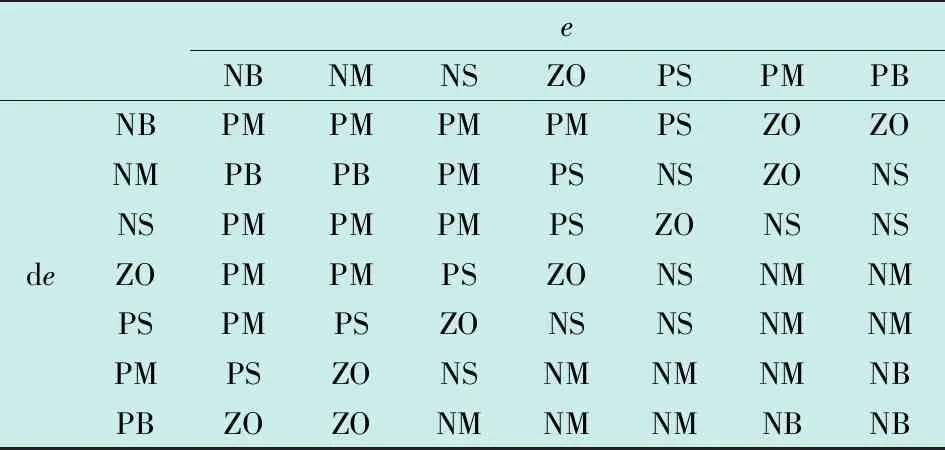
表2 Kp模糊规则

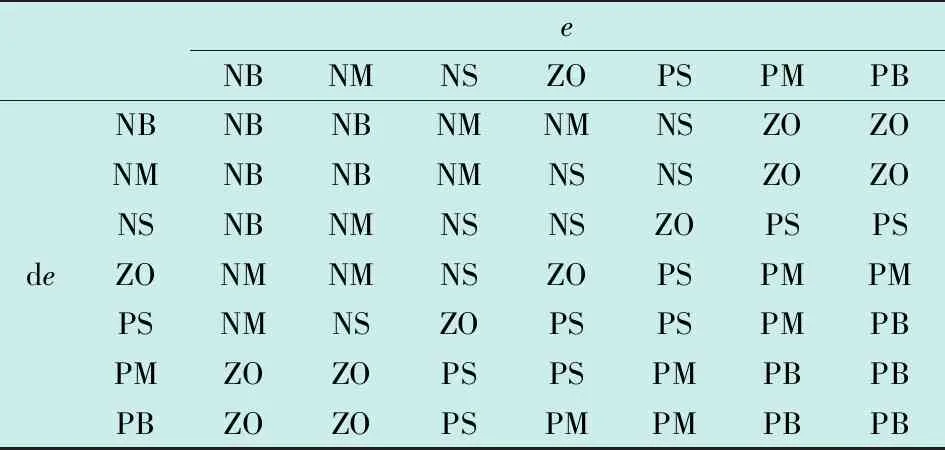
表3 Ki模糊规则

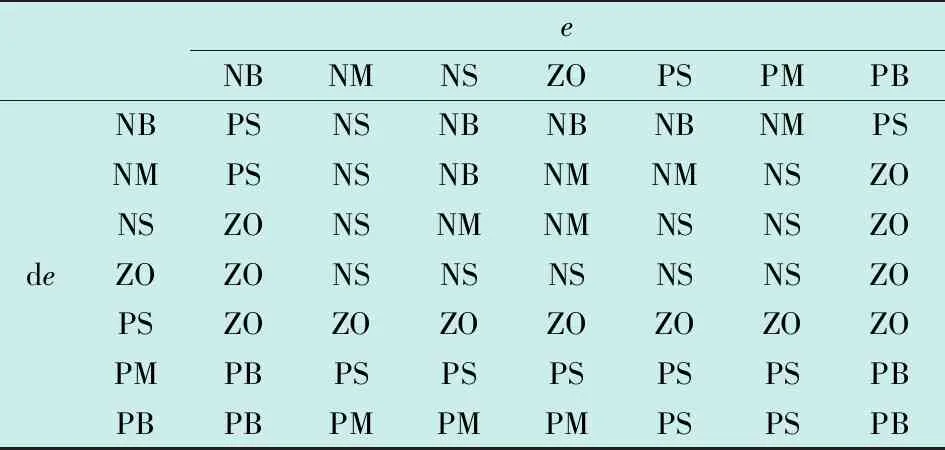
表4 Kd模糊规则

2.3.3 控制策略切换方法

机器人在上电之后,需要在姿态相对平稳的状态下自检,获取传感器数据后解锁开始运动,如果在机器人切换模式后再次自检,可能会出现传感器数据偏移的情况。分析机器人的结构可知,不同的运动模式下机体坐标系是始终重合的,滚动姿态和飞行姿态与内部支撑框架的姿态是完全一致的,由于坐标系的始终重合,因此在不同的运动模式下,机器人进行姿态解算所使用的传感器数据是一样的。为实现控制策略的平滑切换,机器人上电后,完成两种运动模式的自检,处理器同时开始不同运动模式的姿态控制器解算,获得不同模式下执行机构的PWM值,在最终输出环节,通过将不需要的驱动电机PWM值置零的方式限制执行机构运动,当模式切换时,只需将最终的PWM输出数组对应项置零即可实现模式切换,而不必再次进行自检。

这种方式需要处理器有较强的运算能力,针对此问题,采用主处理器与协处理器配合的方式,主处理器为stm32f765,负责运动控制算法的解算,协处理器为stm32f103,负责传感器数据的解算及数据融合,以减小主处理器的运算压力。

3 仿真与实机测试实验

对飞行模式及地面滚动模式下的姿态控制器进行仿真实验,对比模糊PID与串级PID的控制效果,结果如图6所示。

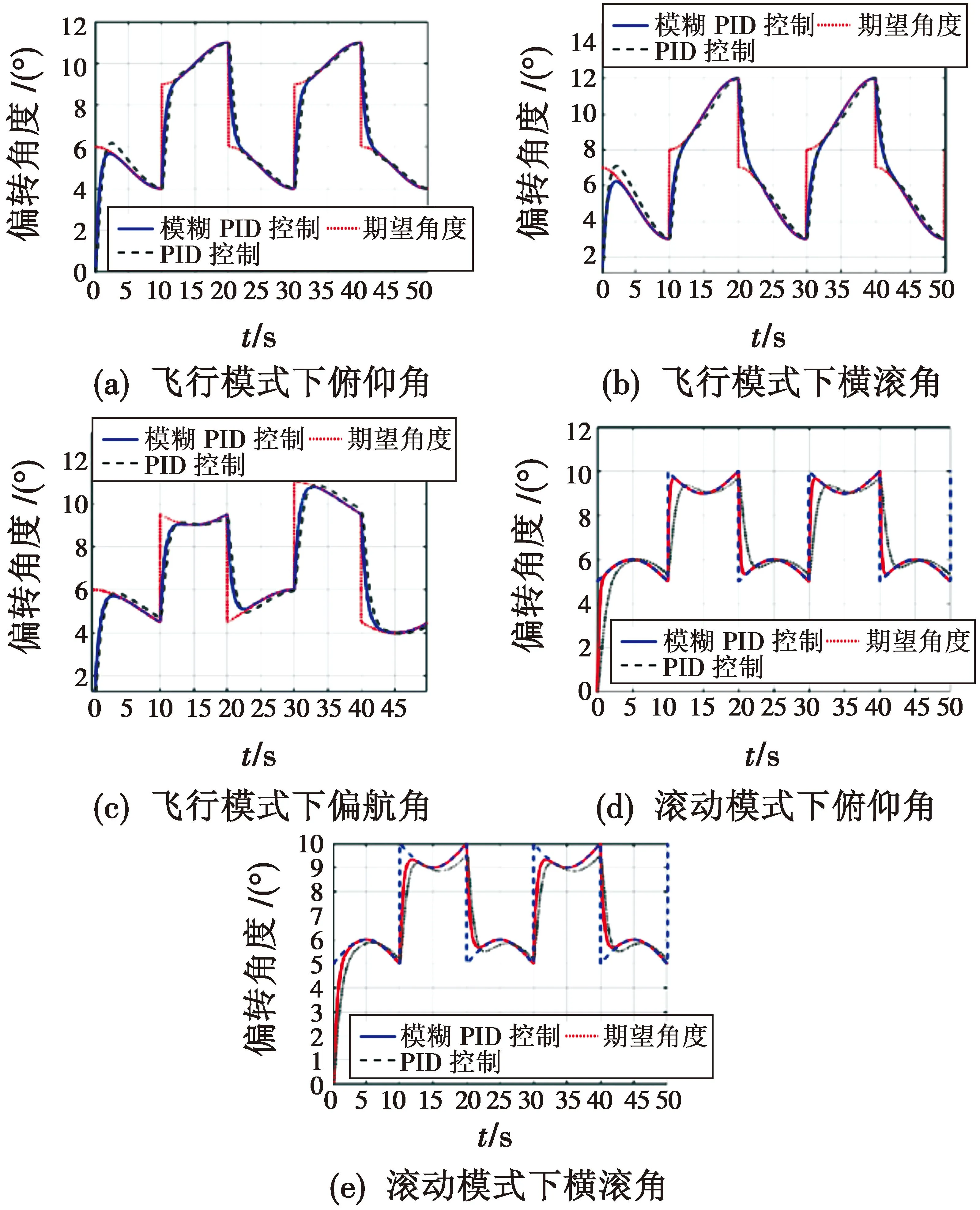
图6 控制器对比仿真结果

根据图6可知,飞行模式下由于系统运动模型准确描述,采用模糊PID的控制方式相较于传统串级PID控制方法提升效果不明显,在得到准确的运动模型前提下,采用串级PID的控制方法可以简单有效地得到很好的控制效果,系统超调量最大为1.6°,在可接受范围之内。在滚动模式下采用模糊PID控制方法可以弥补运动模型无法完全描述的不足,相较于传统串级PID,在超调量及响应时间性能上有明显的提升。

滚动模式下的测试如图7所示。

图7 滚动模式测试

记录运动日志结果如图8所示。

图8 实机测试结果

根据实机测试结果,飞行模式下姿态角控制良好,在落地瞬间会出现姿态不稳,但飞行过程中姿态很稳定。在滚动模式下当期望角度大于35°后,实际俯仰角度无法再跟随期望角度,但在35°以下时,俯仰角可以得到很好的控制效果,分析原因为执行机构输出转矩不够所导致,这为后续的优化做出了指导。

4 结论

本文设计了一种小型空间受限的球形两栖机器人,提出了一种新型的两栖载具模式切换的结构,解决了陆空两栖载具的收桨不确定性问题。建立了机器人的运动模型,针对所建立的运动模型,设计了基于串级PID的飞行姿态控制器以及模糊PID滚动姿态控制器,并通过仿真与实机测试验证了该机器人结构及控制的可行性。通过完整运动流程的实机测试验证,该机器人可以实现12 min的纯飞行运动及1 h以上的纯滚动运动,自主模式切换时间为16 s,具有一定的实际工程意义。