摄像机视场约束下无人机视觉着舰导引方法
2024-03-20祝子程唐超颖徐贵力
祝子程, 王 彪, 唐超颖, 徐贵力
(南京航空航天大学,南京 211000)
0 引言
近年来,无人机的安全着舰已成为一个热门的研究方向。在诸多的机载传感器中,视觉传感器因其获取信息量大、适用范围广、非接触性等特点[1]而成为最重要的传感器之一。将计算机视觉与控制技术结合,视觉伺服(Visual Servoing)技术应运而生,并可按其误差来源分为两类[2],分别是基于位置的视觉伺服(Position-Based Visual Servoing,PBVS)与基于图像的视觉伺服(Image-Based Visual Servoing,IBVS)。
若采用PBVS理论,则可使无人机在飞行空间中较为平稳地跟踪参考轨迹。王忠华等[3]采用图像特征点匹配技术估计出无人机与目标间的相对位姿,利用同步定位与建图(SLAM)技术感知周遭环境、规划路径,最后基于Backstepping理论设计了控制律,实现了无人机的平稳着舰;而为了进一步改善无人机的飞行姿态,韩飞等[4]在采用PBVS理论的同时,引入了基于双滑模面的相对姿轨耦合控制闭环加以辅助,从而实现无人机的安全着舰。但是PBVS理论仅关注飞行空间中的无人机运动,而不关注图像空间中所对应的视觉特征点的运动,导致其容易超出摄像机视场(Field of View,FOV)范围,进而导致着舰失败。
IBVS理论关注图像空间中视觉特征点的运动,能够将图像误差校正为零,具备很高的精确性,非常契合无人机着舰的需要,因而得到学者们的广泛关注。WYNN等[5-6]利用汽车来模拟舰船的运动,并成功应用IBVS理论实现了无人机的安全着舰,针对舰船运动的情况,他们提出了结合前馈速度的IBVS方法,并且实验成功,这些研究成果验证了IBVS理论在无人机着舰任务中的应用潜力。但是,CHAUMETTE等[7]研究发现IBVS理论存在控制效率较低的缺陷,即在图像误差较大时调节能力过强,而在其较小时调节能力较弱。前者可能导致图像空间中视觉特征点的运动轨迹是合理的,但是映射在飞行空间中的无人机运动轨迹是扭曲不合理的;后者可能导致无人机运动过于缓慢。SPONG等[8]在研究中发现当摄像机大幅度旋转时,IBVS理论可能导致视觉特征点超出摄像机视场。因此,引入轨迹规划对其加以改进是有必要的。
LEE[9]从仿生学角度提出了tau理论,指出动物对视觉信息的处理在其接近目标的过程中起导向作用,这与基于IBVS的无人机着舰过程相似;文献[10-11]深入研究了基于tau理论的轨迹规划方法,能够合理规划出无人机在飞行空间中各个时刻的位姿和速度等信息;文献[12-13]则基于此成功实现了无人机降落至期望目标。这些研究成果对本文的研究有着重要的借鉴意义。
李佳欢[14]在研究中发现舰船容易受到海洋风浪等外界扰动作用,同时连带影响到甲板上用以表示无人机降落区域的合作目标及其上的视觉特征点的运动,再加上待整定的系统参数数目也会随着视觉特征点数目增多而增多,所以参数整定工作较为繁冗且复杂。此外,由于IBVS理论通过图像误差收敛的过程来映射无人机飞行轨迹跟踪的过程[15],所以图像误差收敛的动态过程合理即意味着无人机的飞行轨迹较为合理。但是IBVS理论无法直接描述图像误差收敛的动态过程,所以有必要引入与瞬态性能约束相关的控制理论对其进行改进。目前,瞬态性能约束控制理论主要可分为3类,分别为“漏斗”控制(Funnel Control,FC)、障碍李雅普诺夫函数(Barrier Lyapunov Function,BLF)控制和预设性能控制(Prescribed Performance Control,PPC)[16]。其中:FC理论对系统的类型有严格限制,适用场景较为局限;BLF理论需要定义形式特殊的李雅普诺夫函数来辅助设计,且当场景变化时就需要定义新的函数,并且重新设计整个系统,较为不便;PPC理论能够直接描述误差收敛的动态过程,并且能赋予参数整定工作以明确直观的物理意义,从而降低了参数整定的难度。相较FC和BLF理论,PPC理论对系统的类型没有严格限制,适用场景较广,并且无需构造形式复杂的辅助函数,设计过程较为灵活简便[17],非常契合无人机在视觉着舰中的需要。
本文在存在机载摄像机视场范围等约束和海洋风浪扰动的情况下,引入性能约束控制理论,设计了一种轨迹规划与IBVS相容的无人机着舰视觉导引方法。
1 无人机着舰视觉导引方案设计
本文所研究的无人机着舰视觉导引系统主要由视觉处理、tau轨迹规划、导引指令生成与无人机平台4个模块组成,如图1所示。为降低视觉处理算法设计难度,采用高可靠性的ArUco合作目标作为着落标志,并参考文献[18]的相关算法来完成目标检测与识别;位姿解算采用精度较高的PnP算法[19]来实现,并利用Kalman滤波算法进行去噪。总体上,视觉处理工作直接采用成熟可靠的OpenCV库及其拓展包中的solvePnP与滤波等相关函数来实现。在无人机着舰过程中,假设目标舰船的推进系统不工作,舰船运动受到海洋风浪的影响,但较为有限,所以可将由无人机自身IMU所测速度近似作为与舰船间的相对速度使用。因为本文不研究飞行控制器,所以假设控制回路性能理想,将无人机平台视作质心运动学模型来处理。
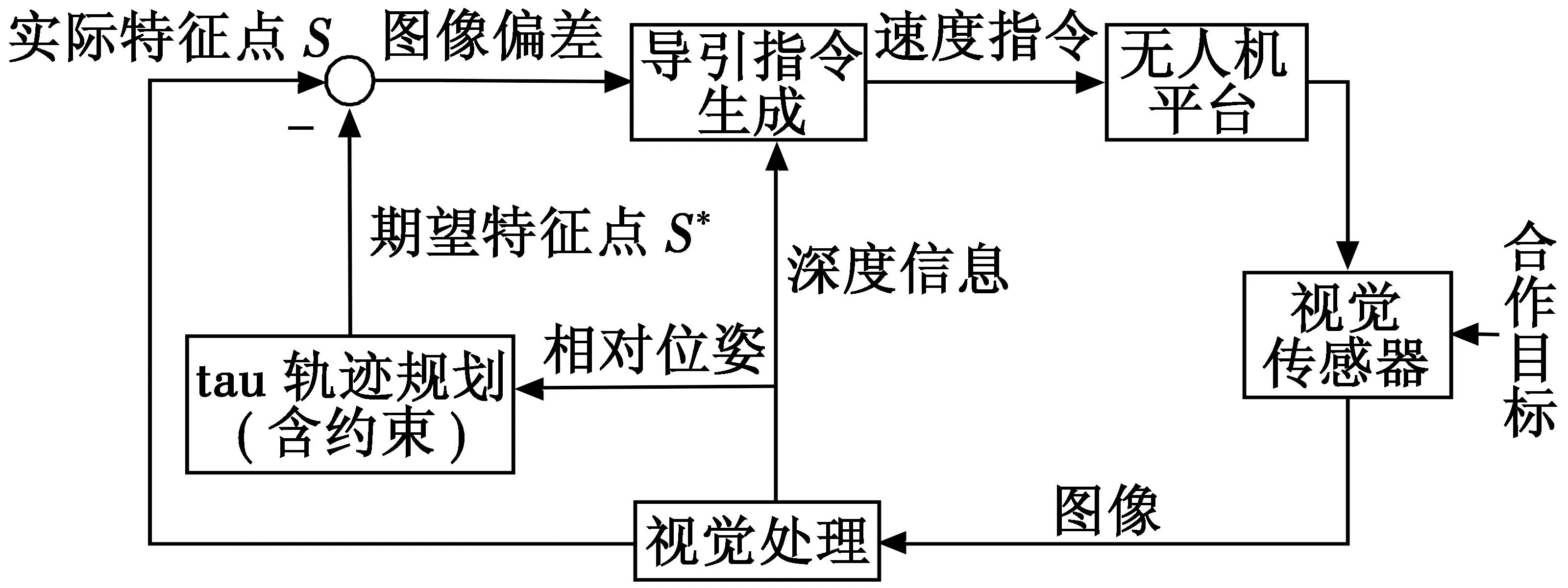
图1 无人机着舰视觉导引系统框图
无人机与合作目标相对位姿如图2所示,本文在目标舰船的甲板上放置了合作目标以表示无人机的降落区域。无人机在飞行过程中通过机载单目摄像机感知周遭环境。当无人机接近舰船后,即可观测到甲板上的合作目标,提取出视觉特征点,并以此计算出自身与舰船间的相对位姿。参照图3,建立机载摄像机的小孔成像模型,则可通过计算来描述飞行空间中的任意一点与归一化像素平面上一点间的映射关系。无人机与舰船间的相对速度信息可根据无人机自身所装配的IMU近似测得。具体为
(1)
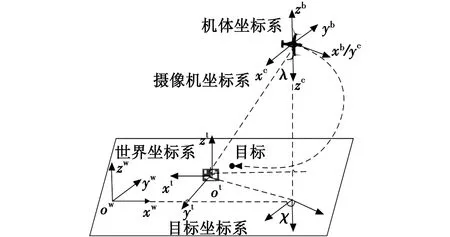
图2 无人机与合作目标相对位姿示意图
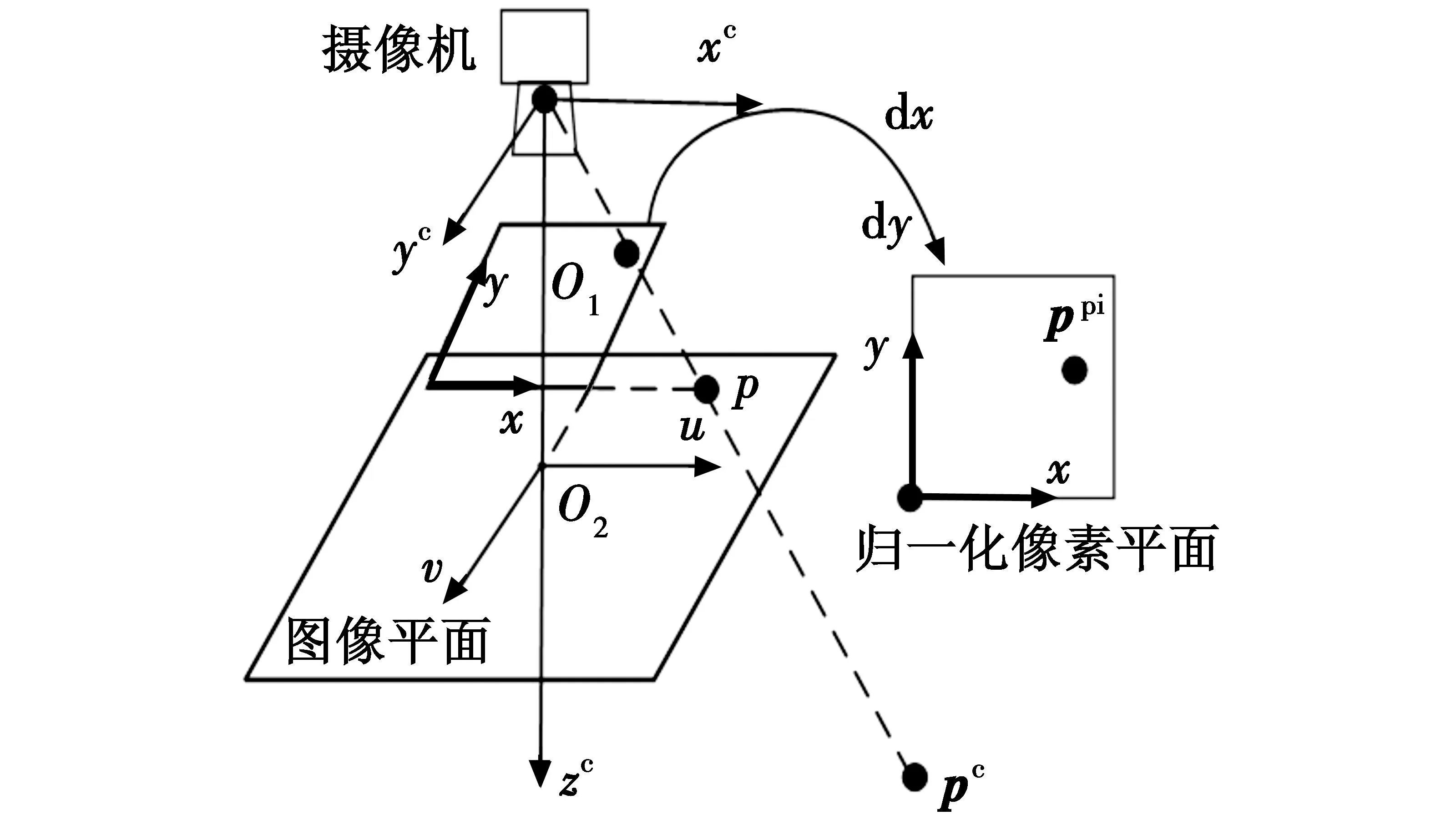
图3 小孔成像模型示意图
(2)
其中:(xw,yw,zw),(xc,yc,zc),分别是点p在世界坐标系和摄像机坐标系中的坐标;ppi=(u,v,1)T,(u,v,1)是其在归一化像素平面的坐标;R、T分别是正交旋转和平移向量;(x0,y0)是主点坐标,fx、fy分别是像平面在x、y两个方向的尺度因子。
至此可结合机载摄像机的视场约束,并基于tau耦合策略规划出一条满足软着舰要求的参考飞行轨迹,并转换至图像空间。之后,对含约束的图像误差进行同胚映射,从而将受限系统转化为等价的不受限系统,并针对该系统设计相应的IBVS控制器以生成导引指令,驱使无人机跟踪参考轨迹直至平稳降落至甲板上的期望位置。整个过程中,通过结合轨迹规划方法与IBVS理论,既改善了无人机的飞行轨迹,使其较为平滑,又能使视觉特征点不会超出摄像机的视场,精准消除图像误差。此外,本文还通过引入PPC理论直接描述图像误差收敛的动态过程,并通过赋予参数整定工作以直观且明确的物理意义以降低其复杂性。
2 视场约束下的tau耦合策略轨迹规划
若仅仅参照IBVS理论,而不规划视觉特征点的轨迹是无法满足无人机平稳着舰需要的。构建如图4所示的轨迹规划模块,引入机载摄像机的视场约束,基于tau耦合策略的轨迹规划方法生成一条满足无人机软着舰要求的参考轨迹。
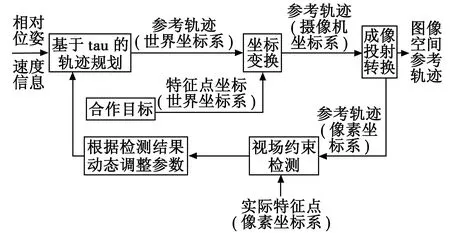
图4 结合tau耦合策略与视场约束的轨迹规划示意图
关于时间的视觉变量tau是设计的关键,其定义为
(3)
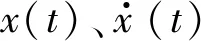
τx(t)=kτy(t)
(4)
则其中一个变量收敛为零的同时,与之对应的其余变量也收敛为零。
确定x(t)对应的tau值后,参照文献[20]计算最优着舰时间td,并取其0.6~0.8倍作为飞行过程中的调头转弯时间tturn。之后,可参照
(5)
规划无人机在着舰过程中与目标间的相对距离。接着,参照
(6)
计算轨迹的末端速度,当其接近零时即可避免无人机猛烈碰撞甲板,使无人机平滑着舰。根据ZHANG等[11]的研究,在区间(0,0.5)内选择k值可使所规划的末端速度接近零,使得参考轨迹满足软着舰要求。最后,可参照
λ(t) =λ0/(x01/kx,λ)*x(t)kx,λ
(7)
χ(t)=χ1(t)+χ2(t)*ε(t-tturn)
(8)
χ1(t)=(χ0-χend,turn)/(x01/kx,χ1)*x(t)1/kx,χ1+χend,turn
(9)
χ2(t)=(χend,turn-χend)/(x01/kx,χ2)*x(t-tturn)1/kx,χ2+χend
(10)
建立所有变量间的耦合关系后,即可根据
p(t)=A*p(td)+B*p(t0)+h
(11)
计算出无人机在飞行过程中的期望位置p(t)。其中,t0为初始时刻;
(12)

(13)
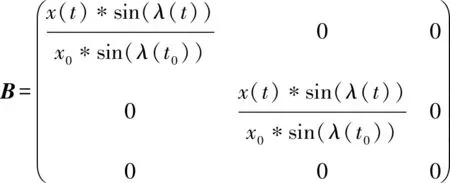
(14)
得到无人机的参考轨迹即得到了摄像机的参考轨迹,参照
pc=T2*R2*(R1*T1*pw+T)
(15)
和图1所示的坐标系将视觉特征点的参考位置转换到摄像机坐标系中。
(16)
(17)
式(16)、式(17)分别表示坐标系的旋转次序和各轴的调换次序,平移向量T由式(1)计算得到。
(18)
根据
(19)
(20)
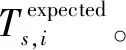
3 结合PPC与IBVS的导引指令生成
PPC理论通过施加额外约束来直接描述被控变量收敛的动态过程和稳态值,即预设合适的性能约束包络边界作为变量的演变区域,从而使其满足要求,该理论能够在保证稳态精度的前提下,兼顾超调量、上升时间和调节时间等动态指标。与此同时,性能约束包络边界也赋予了参数整定工作以直观明确的物理意义,降低其复杂性。本文将PPC与IBVS理论相结合,构建如图5所示的导引系统,生成无人机导引指令,驱使图像误差较平稳地收敛至稳态值,即无人机较平稳地跟踪参考着舰轨迹。
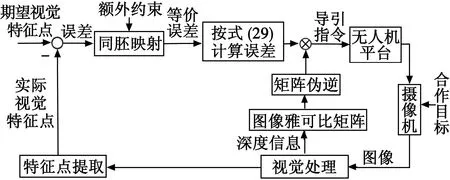
图5 基于PPC与IBVS的导引指令生成框图
定义视觉特征点在归一化像素坐标系中u和v方向上的图像误差为eu,i和ev,i,构造eu,i和ev,i的约束关系,即
(21)

(22)
其中:eu,i(0)和ev,i(0)分别为eu,i和ev,i的初始值;δu,i和δv,i分别为对应eu,i和ev,i的超调量抑制参数;ρu,i(t)和ρv,i(t)分别为对应eu,i和ev,i的性能函数;i=1,…,6。
根据初始图像误差eu,i(0)和ev,i(0)建立约束关系后,选择合理的性能函数ρu,i(t)和ρv,i(t),即
ρu,i(t)=(ρu,i(0)-ρu,i(∞))*e-lu,it+ρu,i(∞)
(23)
ρv,i(t)=(ρv,i(0)-ρv,i(∞))*e-lv,it+ρv,i(∞)
(24)
其中:ρu,i(0)>ρu,i(∞)>0且ρv,i(0)>ρv,i(∞)>0;lu,i>0,lv,i>0,且均为常数。性能函数ρu,i(t)和ρv,i(t)能够使得图像误差按照预设规律收敛,收敛过程的速度受参数lu,i和lv,i影响,而ρu,i(∞)和ρv,i(∞)则定量描述了稳态图像误差的边界。
在确定ρu,i(t)和ρv,i(t)后,构造归一化图像误差zu,i(t)和zv,i(t),即
zu,i(t)=eu,i(t)/ρu,i(t)
(25)
zv,i(t)=ev,i(t)/ρv,i(t)。
(26)
由于引入了额外约束,所以需要寻找到一个合适的同胚映射函数来将受限系统转换成等价的不受限系统,从而降低复杂性。选取同胚映射函数
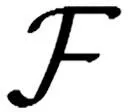
(27)
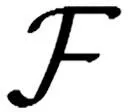
(28)
将归一化图像误差zu,i(t)和zv,i(t)对等映射成新的误差变量εu,i(t)和εv,i(t)。
至此,原受限系统经过同胚映射变换后,即可转换成不受限系统。此时只需设计控制器使得不受限系统中的误差变量有界,就可以将该作用施加在原受限系统中,使其按照预设动态过程工作。
(29)
(30)
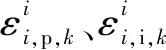
(31)
4 仿真验证
本文依托文献[21]的视景仿真平台对所提出方法的可行性和有效性展开讨论。

由于图像误差收敛的动态过程对应着飞行空间中无人机跟踪参考轨迹的飞行过程,所以当图像误差收敛的动态过程较为平稳时,无人机能够平稳地跟踪上参考轨迹,不会出现剧烈的“抖动”,而图像误差收敛的动态过程是可以直接描述的。
设置u和v方向图像误差的性能约束包络上下边界的初始值分别为±20像素和±15像素,稳态值均为±2像素,收敛速度参数lu,i和lv,i均为0.2,则图像误差在所预设的区域内逐渐收敛为零,如图6(a)所示,调节时间分别为18.1 s和14.7 s,最大偏差分别为14像素和-12像素,作为后续对比基准。

图6 性能约束包络与图像误差变化曲线
通过调节参数lu,i和lv,i可以改变系统的调节时间等,同时也对最大偏差和超调量等有所影响。将参数lu,i和lv,i从0.2增大至0.4,性能包络的收敛速度加快,如图6(b)所示,图像误差收敛的调节时间也随之缩短为12.2 s和11.8 s,最大偏差减小为7像素和-6像素。通过调节性能包络的上下界,可以调整系统的超调量和最大偏差等。保持u和v方向的性能包络的稳态值不变,将初始值分别改为±12像素和±10像素,则性能约束包络边界变窄,而图像误差的峰值也随之减小为5像素和-5像素,如图6(c)所示。
图7(a)表示的是飞行空间中无人机的实际飞行轨迹及其参考着舰轨迹,其中黑色箭头表明无人机的飞行方向,与图6(a)中图像误差的动态收敛过程相对应。综合分析可知,由于图像误差的收敛过程较为平稳,所以无人机在飞行过程中较平稳地跟踪上了参考着舰轨迹,并逐渐接近舰船甲板上的目标位置。图7(b)表示的是无人机在接近目标位置过程中的飞行速度变化情况,可看出,随着无人机逐渐接近待着落的目标位置,其飞行速度逐渐降低,直至在抵达目标位置时速度接近零,即不会与甲板发生剧烈的碰撞。因此,通过本文所提方法,无人机可以安全顺利地着舰。
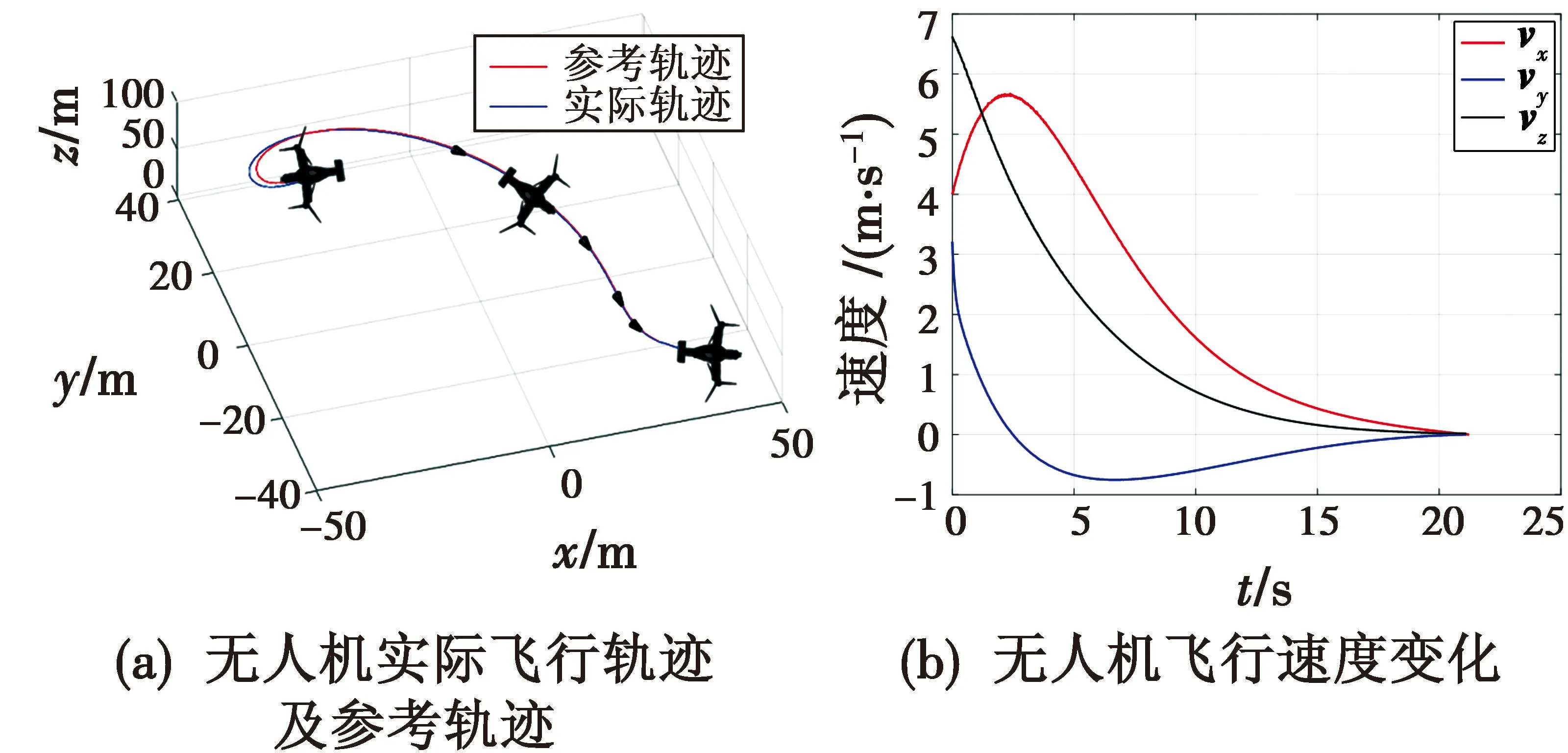
图7 无人机运动轨迹与飞行速度示意图
图8表示的是与图7所对应的图像空间中视觉特征点的运动轨迹,以虚线框表示机载摄像机的视场约束,以多种颜色的圆形和矩形分别表示所选取的6个视觉特征点运动的起点和终点。由于海洋风浪等外界扰动的作用,舰船的运动会受到一定影响,连带影响到舰船甲板上的合作目标及其视觉特征点的运动。由图8可见,视觉特征点的运动虽然受到海洋风浪等外界扰动的影响,但是没有超出虚线框边界,始终处于机载摄像机的视场中。
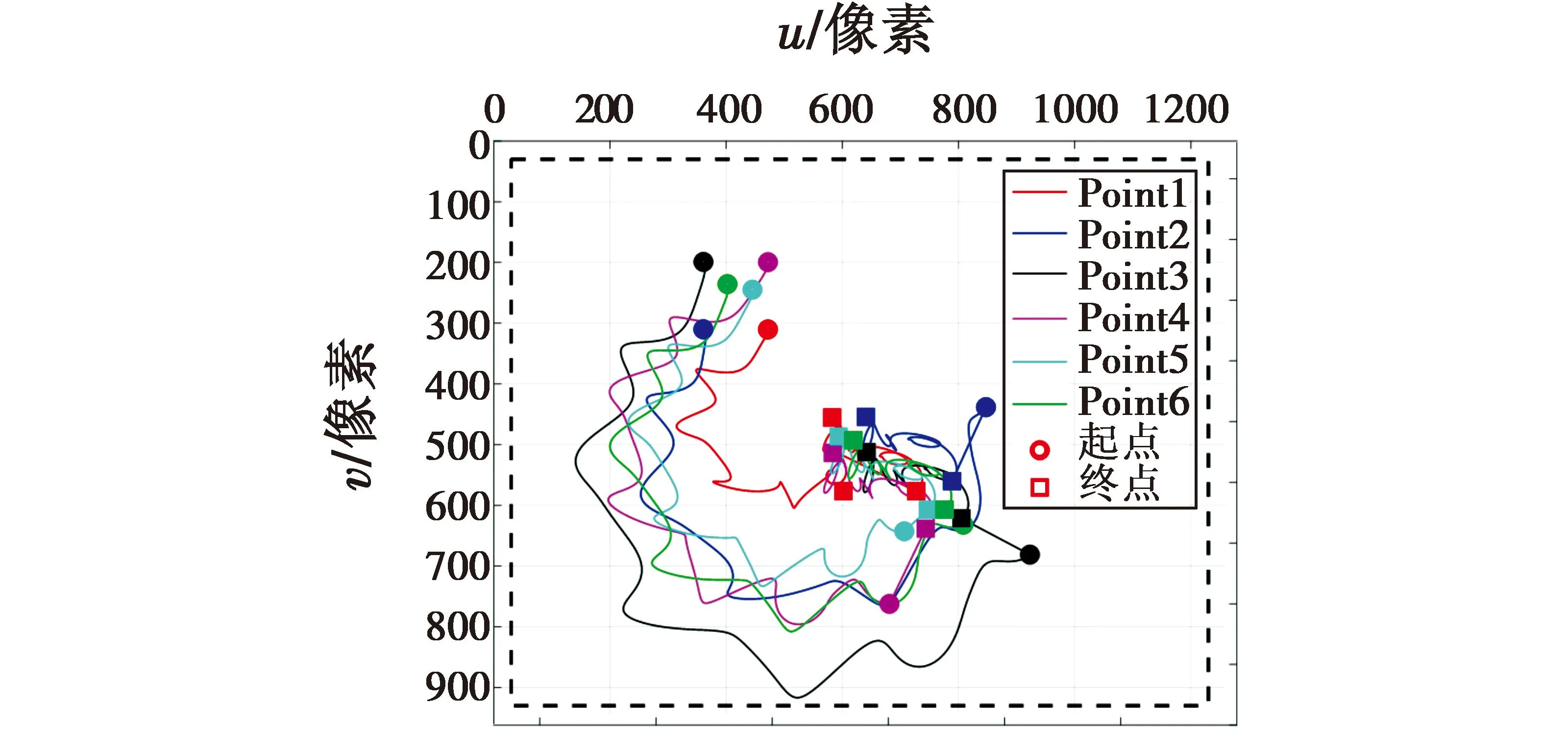
图8 视觉特征点实际运动轨迹
5 结论
本文针对无人机自主视觉着舰研究了一种视觉导引方法,能够使无人机平稳安全地降落至舰船甲板上的期望位置,仿真验证表明本文方法具有以下优势。
1) 引入机载摄像机视场约束对视觉特征点运动做出规划,能有效降低因视觉特征点在运动过程中超视场导致着舰失败的风险,同时可改善无人机的实际飞行轨迹。
2) 引入PPC理论以直接描述图像误差收敛的动态过程,对视觉特征点在图像空间中的运动做出了一定约束,映射至飞行空间,即无人机能够较平稳地跟踪参考着舰轨迹。此外,还赋予了参数整定工作以直观明确的物理意义,降低其复杂性。
