基于人工神经网络智能算法的9310钢本构模型优化

2024-03-20施文鹏孙岑花李佳俊王宇航董显娟

精密成形工程 2024年3期

施文鹏，孙岑花，李佳俊，王宇航，董显娟

施文鹏1，孙岑花1，李佳俊2，王宇航2，董显娟2

（1.江西景航航空锻铸有限公司，江西景德镇 330046；2.南昌航空大学航空制造工程学院，南昌 330063）

研究9310钢在变形温度为800～1 200 ℃、应变速率为0.01～50 s−1和高度压下量为70%条件下的热变形行为，建立预测效果相对较好的9310钢本构模型。使用Gleeble-3800热模拟机对9310钢进行等温恒应变速率热压缩实验，基于热压缩实验数据，分析了应变速率对9310钢流动软化效应的影响，建立了考虑应变补偿的Arrhenius本构模型与支持向量回归（SVR）本构模型，并进行了模型精度分析，之后引入人工神经网络（ANN）智能算法优化了Arrhenius本构模型。与变形温度相比，应变速率对9310钢流动软化效应的影响更为显著。相较于支持向量回归（SVR）本构模型，考虑应变补偿的Arrhenius本构模型精度更高，其相关系数为0.993 4，平均相对误差（AARE）和均方误差（MSE）分别为0.055 6和89.362，它在预测高应变速率（1、10、50 s−1）流动应力时出现了较大偏差，经ANN智能算法优化后，相关系数提高至0.999 1，AARE和MSE分别降至0.019 9和9.998，且绝对误差在±10 MPa以内的预测流动应力占比为98.34%。在低应变速率（0.01 s−1）下软化效应更强，在高应变速率（10 s−1）下再结晶程度较低，软化效应较弱。ANN智能算法优化后的Arrhenius本构模型具有较高的精度，能较准确地预测9310钢的流动行为。

9310钢；本构模型；Arrhenius型本构模型；人工神经网络（ANN）；智能算法优化

9310钢具有优异的综合性能，如强度高、韧性好等[1]。在钢的成形过程中，热变形行为是一个重要问题，而材料的本构模型可以系统地描述热变形工艺参数与流动应力之间的关系，为有限元模拟提供数据支撑，同时可为材料热加工参数的选择提供参考[2]。

通常，钢在高温下的热变形行为总是表现出各种相互关联的冶金现象，如加工硬化等，这使得热变形行为建模相当复杂[3-4]。大多学者[5-6]采用Arrhenius型方程来构建本构模型，然而模型的预测精度十分有限。于是有学者在其基础上考虑了应变补偿，如Li等[7]将考虑了应变补偿的Arrhenius本构模型引入有限元模型中，验证了该本构模型的有效性。刘江林等[8]采用回归分析和多项式拟合方法，建立了基于应变补偿的本构模型，该模型可精确预测应变速率小于1 s−1时的流动应力。尽管唯象型本构模型一直被认为是预测流动行为的有效方法[9]，但数学建模的高度复杂性限制了其广泛应用。随着人工智能在材料领域的发展，机器学习（ML）被用于构建本构模型，并在过去的几年中得到了广泛的应用[10-11]。在不涉及物理机制的情况下，ML方法可以表现出优异的预测性能[12-13]，已经有许多学者利用不同种类的智能算法来构建工艺参数和流动应力之间的本构关系，例如，Rezaei等[14]采用人工神经网络（ANN）模型来描述和预测热变形条件下纯铝的流动行为，结果表明，所建立的神经网络模型是预测纯铝复杂非线性热流动行为的有效方法。此外，还有支持向量回归（SVR）方法[15]等。截至目前，也有学者对9310钢的流动行为进行了预测，如黄顺喆等[16]根据动态再结晶是否发生，建立了不同热变形阶段下9310钢的流动应力本构方程，其预测精度分别控制在15%与10%以内，精度较低。因此，有必要构建一种预测精度相对较高的9310钢本构模型。

本文根据9310钢热压缩实验数据，分析了应变速率对9310钢软化效应的影响，建立了考虑应变补偿的Arrhenius型本构模型、支持向量回归（SVR）本构模型和人工神经网络（ANN）智能优化的Arrhenius型本构模型来预测9310钢的流动应力，并进行了对比，以期为9310钢锻造过程有限元数值模拟提供数据支撑。

1 实验

实验材料为锻态9310钢棒料，试样的尺寸为8 mm×12 mm，化学成分如表1所示。采用Gleeble- 3800热模拟实验机进行9310钢等温恒应变速率热压缩实验，实验温度为800～1 200 ℃，中间间隔50 ℃，共9个温度。应变速率分别为0.01、0.1、1、10、50 s−1。整个热压缩和冷却过程都在真空下进行，以5 ℃/s的速率加热升温到实验温度，保温3 min后进行压缩，高度压下量为70%（真实应变约为1.2），压缩结束后迅速水冷至室温，以保留变形组织，通过实验机自带的传感器记录9310钢试样的应力-应变曲线。

将压缩后的9310钢试样切开并镶嵌，选用800#～2000#的金相砂纸进行打磨，抛光后用体积分数为4%的硝酸酒精溶液腐蚀金相试样20 s，最后使用光学显微镜观察试样的微观组织。9310钢的原始组织如图1所示，主要为板条马氏体+少量的残余奥氏体组织。

表1 9310钢的化学成分

Tab.1 Chemical composition of 9310 steel wt.%

图1 9310钢原始组织

2 实验结果

2.1 9310钢流动应力曲线

不同工艺参数下9310钢的流动应力曲线如图2所示。可以看出，与变形温度相比，应变速率对9310钢流动软化效应的影响更为显著。如图2c所示，在低应变速率0.01 s−1下，变形初期流动应力急剧上升，这是由于位错的增殖、攀移以及位错间的相互作用使位错密度迅速累积而产生加工硬化；随着应变的进一步增大，在达到临界应变之后，动态回复（DRV）和动态再结晶（DRX）开始发生，软化效应逐渐增强，流动应力开始下降；最后，软化与硬化效应达到平衡，流动应力逐渐趋于稳定[17]。可见，在低应变速率下软化效应更强，更有利于发生动态再结晶。值得注意的是，在温度1 000～1 200 ℃变形时，当应变量增到0.7时，流动应力又开始缓慢上升，表现出加工硬化特征。从图2d可以看出，在高应变速率10 s−1下，流动曲线呈现宽应力峰，这一般是发生动态回复的典型特征[18]，由于高的应变速率变形时间较短，达到临界应变所需的应变量更大，再结晶程度较低，因此软化效应较弱，流动应力下降缓慢。

9310钢在不同变形参数下的显微组织如图3所示。可以看出，在低温低应变速率下，奥氏体晶粒尺寸十分细小，且基本为等轴晶状，有许多颗粒状的M23C6和M7C3碳化物析出，如图3a所示[19]。随着变形温度的升高，再结晶晶粒发生了长大，这是由于当应变速率一定时，随着变形温度的升高，晶界可动性增强，有利于发生动态再结晶的形核及晶粒长大[20]。在低应变速率（0.01 s−1）下的高温段（1 000～1 200 ℃），当应变量增至0.7时，在晶界表面能的驱动下，新晶粒相互吞食而重新开始长大，流动应力表现出加工硬化特征。从图3b可以看到奥氏体晶粒尺寸的增大与大量板条状马氏体群的生成。在高应变速率（10 s−1）下，变形时间较短，再结晶程度较低，如图3c所示。图3d为1 200 ℃/10 s−1下的显微组织，随着变形温度的进一步升高，奥氏体晶粒发生了明显长大，使板条马氏体粗化。

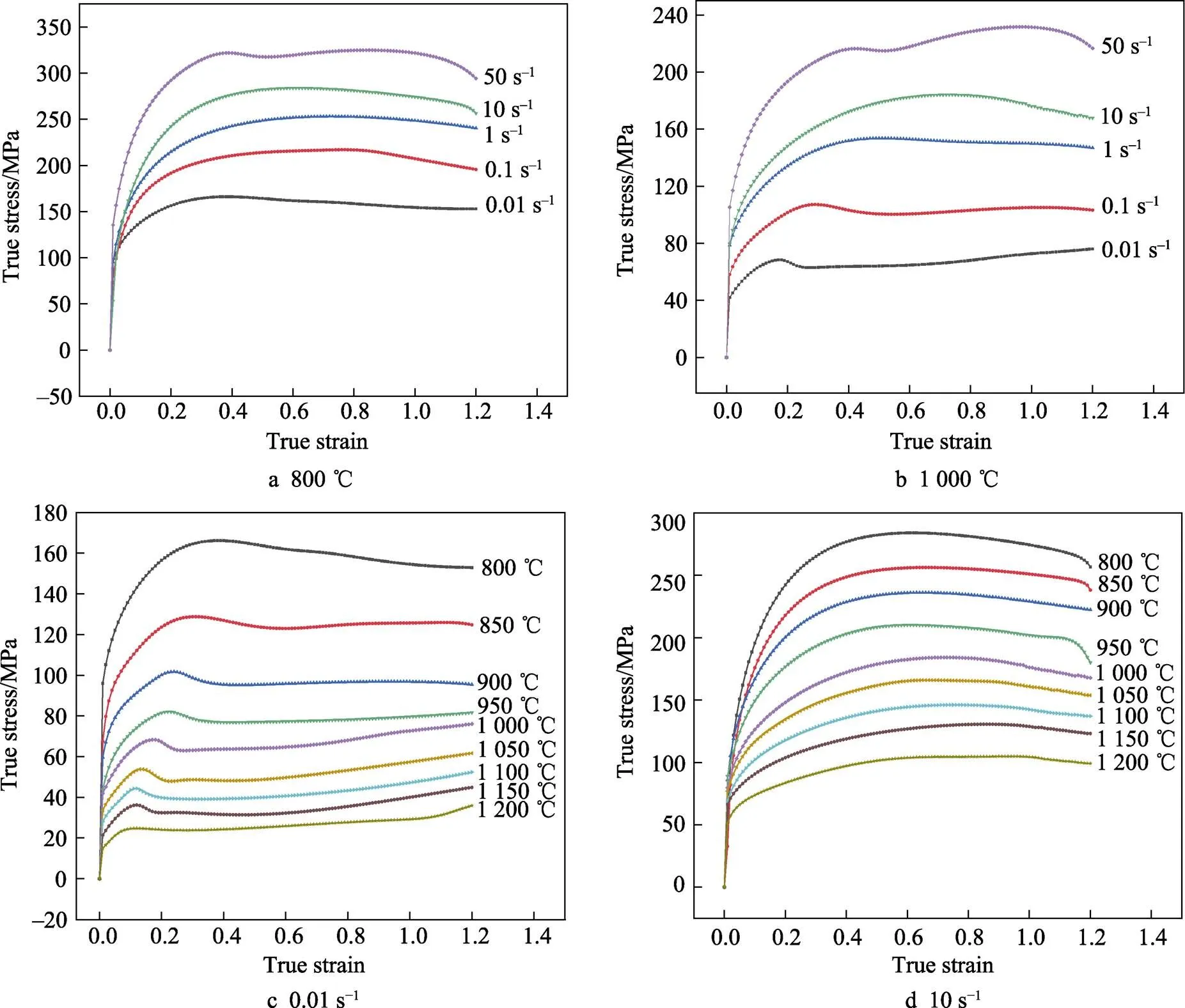
图2 不同工艺参数下9310钢的流动应力曲线

图3 不同变形参数下9310钢的显微组织

2.2 9310钢本构模型的建立

2.2.1 考虑应变补偿的Arrhenius型本构模型

本构方程可以描述不同热变形条件与流动应力之间的关系，从而对热变形过程进行预测。目前，使用最广泛的是Arrhenius型双曲正弦函数本构模型，已经在多种材料中得到了应用[21]，该方程表达式如式（1）～（3）所示。

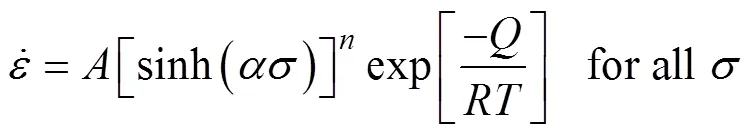
由式（1）～（4）可得到本构模型如式（5）所示。

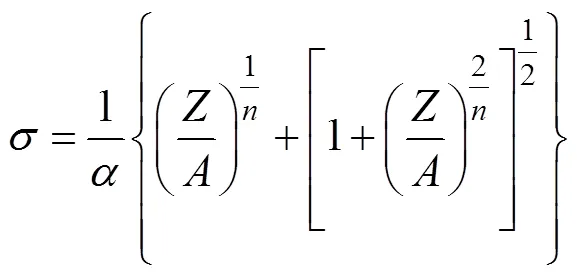
对式（1）～（4）两边同时取对数，可由关系曲线的平均斜率得到材料常数ln，之后将所得到的材料常数代入式（5），便可得到9310钢的Arrhenius型本构模型。

在单一应变下构建的Arrhenius型本构模型不能确切地描述该钢全程变形的流动行为，故可以将应变耦合到材料常数中。以应变0.1为间隔，分别计算出应变为0.1～1.2时所对应的材料常数，建立应变与材料常数ln的多项式函数关系，通过对数据进行3～7阶多项式对比，发现6阶多项式的拟合精度最好，拟合效果如图4所示，拟合多项式方程如式（6）～（9）所示。

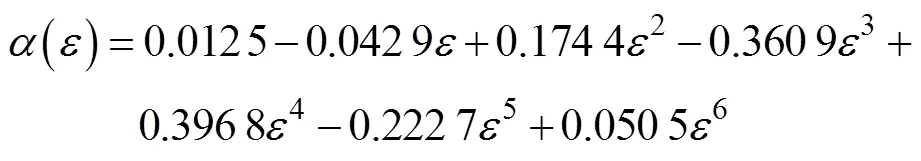
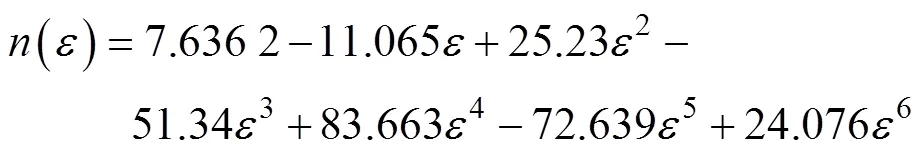
图4 材料常数与真应变的拟合函数关系曲线

在式（5）的基础上，考虑应变的影响，将式（6）～（9）代入式（5），可得到考虑应变补偿的9310钢Arrhenius型本构模型，如式（10）所示。

2.2.2 支持向量回归（SVR）本构模型

支持向量机（SVR）算法通常是模拟线性和非线性数据集的合适算法之一，由Cortes等[22]提出。支持向量回归（SVR）是SVM的一种延伸，可以有效地完成非线性拟合。其原理是找到一个回归平面，让一个集合的所有数据到该平面的距离最近。与一般回归不同的是，支持向量回归会允许模型有一定的偏差，也就是在决策边界之内的点，模型不认为它们有问题。

SVR模型的工作原理如图5所示。通常在样本空间中有无穷多个超平面，而认为那些在决策边界以内且距离超平面还有一段距离的点最好，因为这样能够使模型具有较好的泛化能力，这些点也被称为支持向量。如图5所示，由中间的超平面产生的分类结果最为稳定，能够最大限度地承受训练样本的局部扰动，具有最强的泛化能力。考虑到变形温度、应变速率和应变量对流动行为的影响，SVR模型以这3个工艺参数为输入变量、以流动应力为输出变量进行训练、建模和预测。

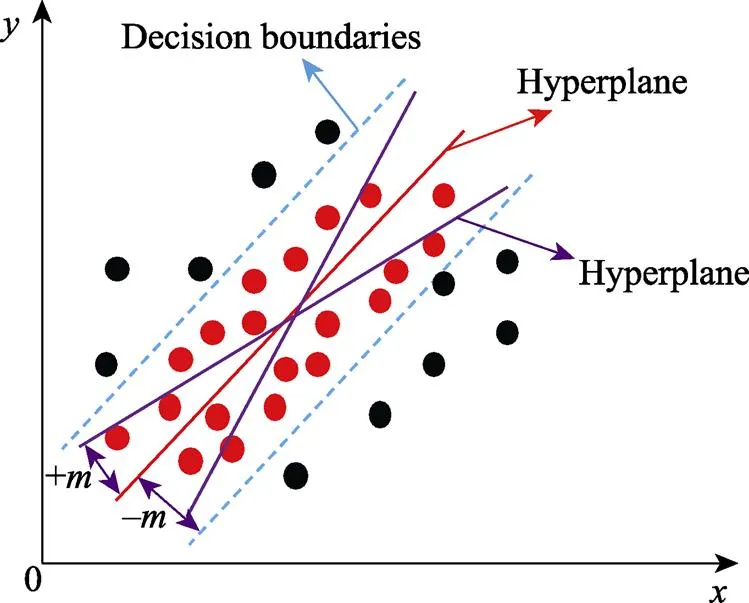
图5 SVR模型的工作原理

基于考虑应变补偿的Arrhenius本构模型和支持向量回归本构模型，9310钢800 ℃时流动应力的预测结果如图6所示。可以看出，在高应变速率（1、10、50 s−1）下，考虑应变补偿的Arrhenius本构模型的预测值（见图4a中虚线圈出部分）偏离实验值较大，在其他应变速率下，预测值与实验值吻合较好。支持向量回归（SVR）模型在高应变速率下则表现出较高的贴合度，在预测低应变速率（0.01 s−1和0.1 s−1）流动行为时显示出较大的预测误差（见图4b虚线标出部分）。可见，这2种本构模型均不能准确地预测9310钢的流动应力。

图6 800 ℃下的流动应力曲线预测对比

2.3 基于人工神经网络智能算法优化的Arrhenius本构模型

人工神经网络（ANN）作为智能算法中的一种，能够模拟人脑在决策过程中的工作过程，具有良好地捕捉输入输出之间高度非线性复杂关系的能力[23]。如图7所示，ANN模型由输入层、输出层和一个或多个隐藏层组成，这些隐藏层由称为神经元的处理单元连接。根据是否有监督[24]，人工神经网络被分为时间依赖神经网络、前馈神经网络和递归神经网络等[25]。

针对考虑应变补偿的Arrhenius本构模型和支持向量回归本构模型在预测流动应力过程中存在的问题，本文基于人工神经网络（ANN）智能算法对Arrhenius型本构模型的预测误差进行优化。预测误差如式（11）所示。ANN优化后的最终预测应力如式（12）所示[26]。

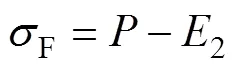
ANN模型中使用的参数如表2所示，其中输入变量包括变形温度、应变速率和应变量，输出为绝对误差。此外，隐藏层神经元数目的选取是一个非常复杂的问题，通常根据实验或研究者的经验来确定。如果模型的结构过于简单，则训练好的网络可能不具有足够的能力来正确学习。相反，如果结构太复杂，则它在训练期间可能不收敛，或者训练的数据可能过拟合。因此，为了确定合适的隐藏层神经元数目，通常采用试错法来评估最优的神经网络。由于ANN算法中的权重和偏置的原始值具有一定的随机性，因此，在每次计算给定ANN的平均绝对误差（MAE）时，它们都不相同。为了克服人工神经网络的随机性，对每个固定隐藏层数的人工神经网络进行10次训练，然后选出最小的MAE作为该人工神经网络的最终平均绝对误差。最后，确定了此次ANN模型的隐藏神经元数目为20。

表2 ANN中使用的参数

Tab.2 Parameters used in ANN

3 分析与讨论

为了进一步探究以上3种本构模型的优劣，下面将从不同变形参数下的流动应力预测、相关系数、平均相对误差、均方误差以及绝对误差分布5个方面，评估3种本构模型的预测能力和精度。

3.1 流动应力曲线

3种模型在800、1 000、1 200 ℃时的实验流动应力与预测流动应力如图8所示。可以看出，在不同变形参数下，基于人工神经网络（ANN）智能算法优化后的Arrhenius模型不仅能够精确地预测流动应力，还能很好地拟合9310钢的加工硬化区和动态软化区。这是因为支持向量回归的本构模型的预测精度受到多种因素影响，如核函数的选取、参数的调控以及样本数目等，模型本身也允许一定的偏差存在，这会导致预测不准确。考虑应变补偿的Arrhenius本构模型在求解材料常数和1时，所采用的公式分别为高应力水平下的式（2）和低应力水平下的式（1），然后对其进行了取平均值运算，其他的材料常数又是基于和1的平均值进行计算的，因此误差较大。通过ANN对Arrhenius本构模型误差进行智能优化后，由线性误差转换成了高维的非线性映射，提高了对加工硬化区和动态软化区的预测效果，能很好地描述9310钢流动应力、工艺参数和应变之间的非线性关系。值得一提的是，若直接采用ANN构建本构模型，由于ANN本身的随机性，会不可避免地产生一定的预测误差，而ANN优化Arrhenius本构模型误差的过程是一个误差相互抵消的过程，因此最终的预测精度会有显著的提升。

3.2 相关系数、平均相对误差和均方误差

在评估一个模型的优劣时，应该从多方面进行评判。通常，本构模型采用相关系数、平均相对误差和均方误差等来衡量实验流动应力与预测流动应力之间的偏差，其表达式如式（13）～（15）所示。

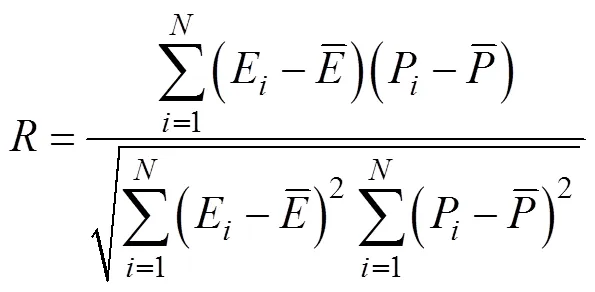
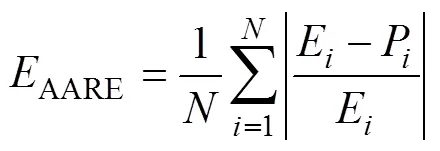
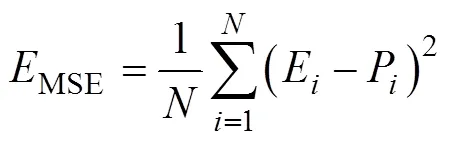
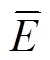
图8 3种模型的预测流动应力与实验流动应力

3种模型的实验流动应力与预测流动应力的相关性如图9所示。可以看出，在流动应力达到200 MPa以后，考虑应变补偿的Arrhenius模型的离散程度较高，该模型在高应变速率下会导致预测发生偏离，而支持向量回归（SVR）模型在200 MPa以下则是离散的。与SVR模型相比，考虑应变补偿的Arrhenius本构模型的相关系数（0.993 4）更高。而基于人工神经网络对Arrhenius本构模型进行智能优化后，相关系数达到了0.999 1，相关性较强。

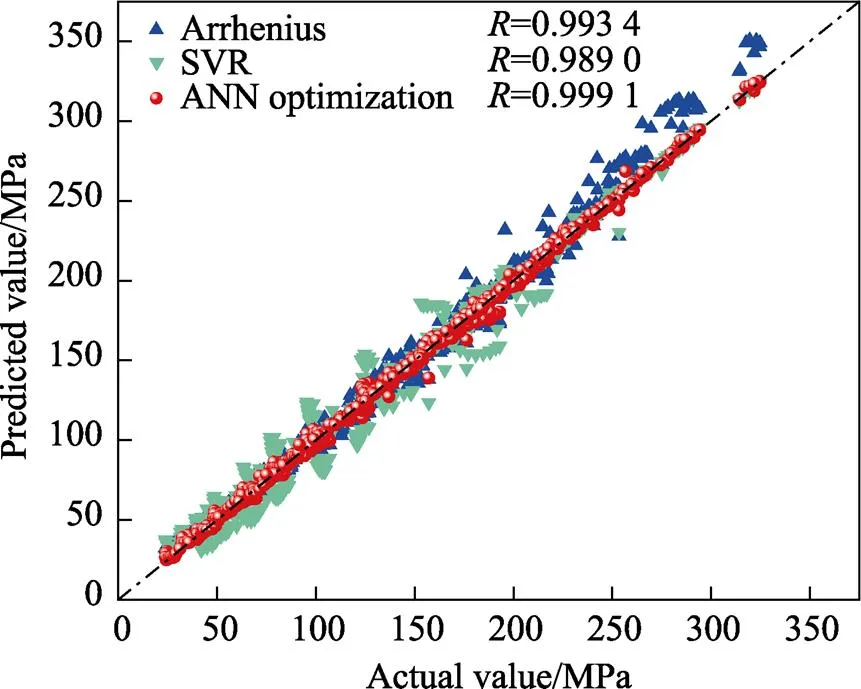
图9 3种模型实验值与预测值的相关性比较

3种模型的平均相对误差（AARE）和均方误差（MSE）如图10所示。可以看出，考虑应变补偿的Arrhenius本构模型的平均相对误差（0.055 6）和均方误差（89.362）分别比SVR模型的低了0.018 9和26.479，说明该模型的精度相对要高一些。但与前面2种模型相比，经人工神经网络智能优化后，Arrhenius型本构模型的平均相对误差（0.019 9）和均方误差（9.998）大幅度降低，预测精度明显提高。

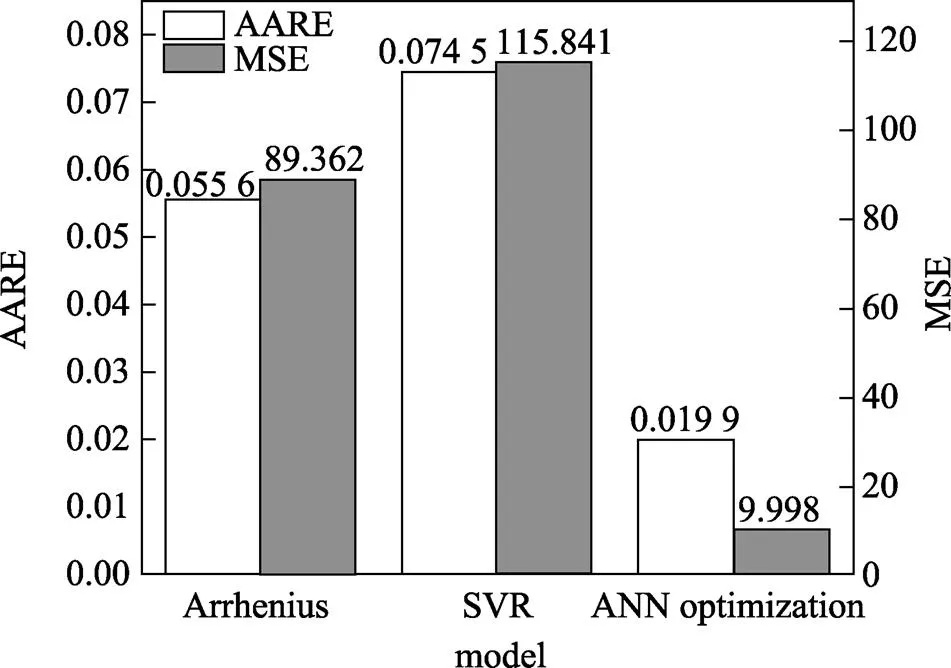
图10 3种模型的平均相对误差和均方误差对比

3.3 绝对误差

为了进一步对比考虑应变补偿的Arrhenius本构模型与人工神经网络（ANN）智能算法优化后的模型之间的差距，对2种模型的绝对误差分布进行了比较，如图11所示。可以看出，优化后的模型绝对误差分布更加集中，绝对误差在±10 MPa以内的预测流动应力达到了98.34%，而考虑应变补偿的Arrhenius本构模型绝对误差在±10 MPa以内的预测流动应力只占82.04%。综上可知，ANN智能算法优化后的Arrhenius本构模型的精度较高，能更好地预测9310钢流动行为。

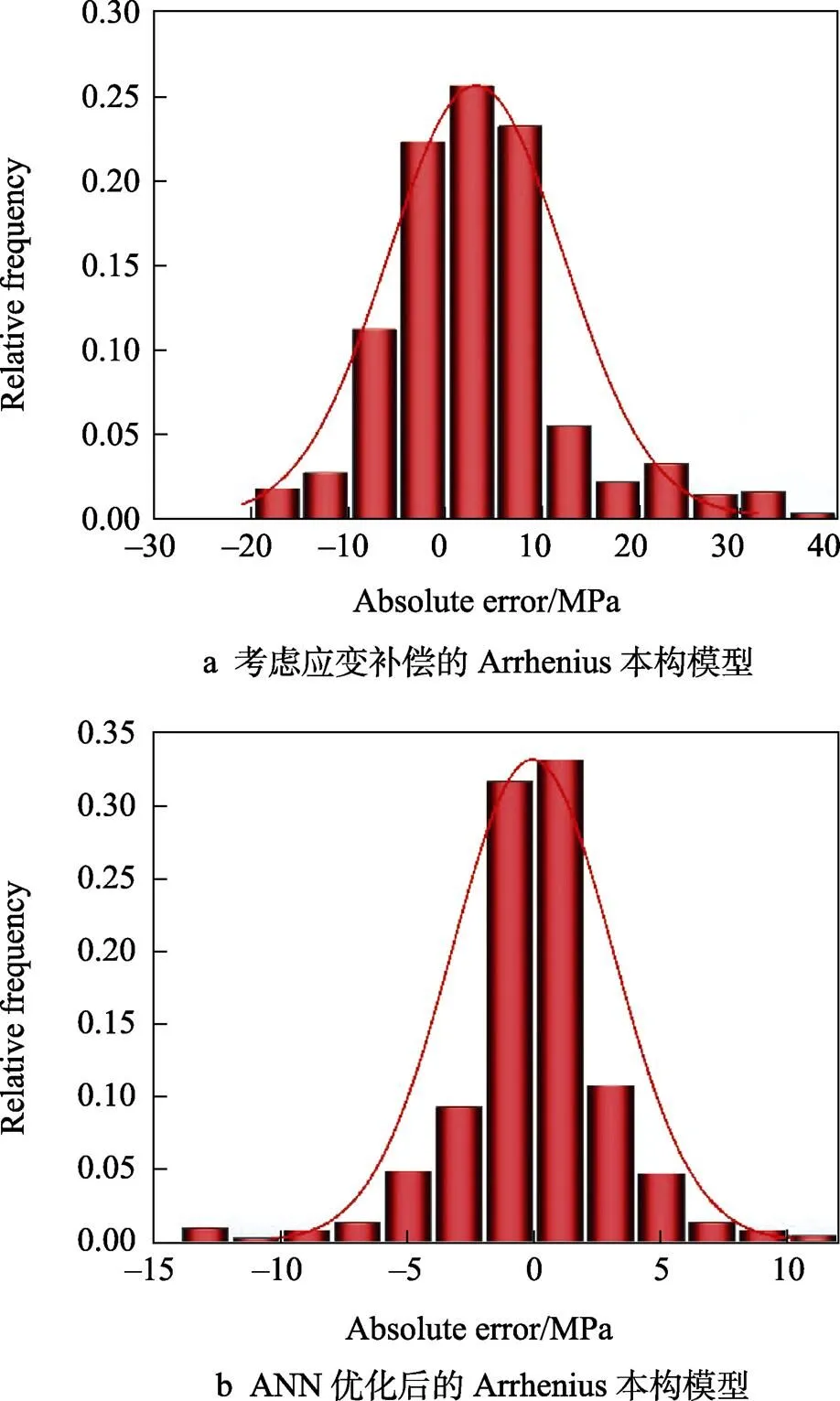
图11 绝对误差分布

4 结论

1）与变形温度相比，应变速率对9310钢流动软化效应的影响更为显著。在低应变速率（0.01 s−1）下软化效应更强，在温度为1 000～1 200 ℃条件下，当应变量增到0.7时，流动应力又开始缓慢上升，表现出加工硬化特征。在高应变速率（10 s−1）下再结晶程度较低，软化效应较弱。

2）建立了考虑应变补偿的Arrhenius型本构模型和支持向量回归（SVR）本构模型，相较于SVR模型，考虑应变补偿的Arrhenius本构模型精度更高，其相关系数为0.993 4，平均相对误差和均方误差分别为0.055 6和89.362，但在预测高应变速率（1、10、50 s−1）下的流动应力时出现较大偏差。

3）采用人工神经网络（ANN）智能算法对考虑应变补偿的Arrhenius型本构模型进行了优化，相关系数达到了0.999 1，平均相对误差（0.019 9）和均方误差（9.998）大幅度降低，绝对误差在±10 MPa以内的预测流动应力占比为98.34%，能够较准确地预测9310钢的流动应力。

[1] 吴秋平, 王春旭, 刘宪民, 等. 回火温度对9310钢力学性能及组织的影响[J]. 热加工工艺, 2012, 41(6): 179-180.

WU Q P, WANG C X, LIU X M, et al. Influence of Tempering Temperature on Mechanical Properties and Microstructure of 9310 Steel[J]. Hot Working Technology, 2012, 41(6): 179-180.

[2] 田茂森, 陈刚, 沈四喜, 等. 52CrMoV4弹簧钢热变形行为的本构模型[J]. 有色金属工程, 2023, 13(3): 49-60.

TIAN M S, CHEN G, SHEN S X, et al. Constitutive Model of Hot Deformation Behavior of 52CrMoV4 Spring Steel[J]. Nonferrous Metals Engineering, 2023, 13(3): 49-60.

[3] LIN Y C, CHEN X M, GE L. A Modified Johnson-Cook Model for Tensile Behaviors of Typical High-Strength Alloy Steel[J]. Materials Science and Engineering A, 2010, 527(26): 6980-6986.

[4] SAADATKIA S, MIRZADEH H, CABRERA J M. Hot Deformation Behavior, Dynamic Recrystallization, and Physically-Based Constitutive Modeling of Plain Carbon Steels[J]. Materials Science & Engineering A, 2015, 636: 196-202.

[5] BROWN C, MCCARTHY T, CHADHA K, et al. Constitutive Modeling of the Hot Deformation Behavior of CoCrFeMnNi High-entropy Alloy[J]. Materials Science and Engineering: A, 2021, 826: 141940.

[6] 杨晓康, 王快社, 史佳敏, 等. TC17钛合金高温变形行为研究[J]. 稀有金属材料与工程, 2018, 47(9): 2895-2900.

YANG X K, WANG K S, SHI J M, et al. High Temperature Deformation Behaviour of TC17 Titanium Alloy[J]. Rare Metal Materials and Engineering, 2018, 47(9): 2895-2900.

[7] LI H, LANG M W, SHI L X, et al. Study on Hot Deformation Behavior of Homogenized Mg-8.5Gd- 4.5Y-0.8Zn-0.4Zr Alloy Using a Combination of Strain- Compensated Arrhenius Constitutive Model and Finite Element Simulation Method[J]. Journal of Magnesium and Alloys, 2021, 11(1): 1851-1859.

[8] 刘江林, 曾卫东, 谢英杰, 等. 基于应变补偿TC4-DT钛合金高温变形本构模型[J]. 稀有金属材料与工程, 2015, 44(11): 2742-2746.

LIU J L, ZENG W D, XIE Y J, et al. Constitutive Model of TC4-DT Titanium Alloy at Elevated Temperature Considering Compensation of Strain[J]. Rare Metal Materials and Engineering, 2015, 44(11): 2742-2746.

[9] GUO N N, WANG L, LUO L S, et al. Hot Deformation Characteristics and Dynamic Recrystallization of the MoNbHfZrTi Refractory High-Entropy Alloy[J]. Materials Science and Engineering A, 2015, 651: 698-707.

[10] QIAO L, WANG Z B, ZHU J C. Application of Improved GRNN Model to Predict Interlamellar Spacing and Mechanical Properties of Hypereutectoid Steel[J]. Materials Science and Engineering A, 2020, 792(1): 139845.

[11] LIN Y C, HUANG J, LI H B, et al. Phase Transformation and Constitutive Models of a Hot Compressed TC18 Titanium Alloy in the α+β Regime[J]. Vacuum, 2018, 157: 83-91.

[12] QIAO L, DENG Y, LIAO M Q, et al. Modelling and Prediction of Thermal Deformation Behaviors in a Pearlitic Steel[J]. Materials Today Communications, 2020, 25: 101134.

[13] ZHU Y L, CAO Y, LIU C J, et al. Dynamic Behavior and Modified Artificial Neural Network Model for Predicting Flow Stress during Hot Deformation of Alloy 925[J]. Materials Today Communications, 2020, 25: 101329.

[14] REZAEI A H R, SHAYANPOOR A A. Hot Deformation Characterization of Pure Aluminum Using Artificial Neural Network (ANN) and Processing Map Considering Initial Grain Size[J]. Metals and Materials International, 2021, 27(12): 5017-5033.

[15] NIU Y, HONG Z Q, WANG Y Q, et al. Machine Learning-Based Beta Transus Temperature Prediction for Titanium Alloys[J]. Journal of Materials Research and Technology, 2023, 23(9): 515-529.

[16] 黄顺喆, 厉勇, 王春旭, 等. 高强渗碳钢高温热变形的本构方程[J]. 材料热处理学报, 2014, 35(10): 210- 217.

HUANG S Z, LI Y, WANG C X, et al. Constitutive Equations of a High-Strength Carburizing Steel during High Temperature Thermal Deformation[J]. Transactions of Materials and Heat Treatment, 2014, 35(10): 210-217.

[17] 彭嘉豪, 孙前江, 周建伟, 等. TC4-DT钛合金高温热变形及加工[J]. 中国有色金属学报, 2022, 32(4): 994-1003.

PENG J H, SUN Q J, ZHOU J W, et al. High Temperature Thermal Deformation and Processing of TC4-DT Titanium Alloy[J]. The Chinese Journal of Nonferrous Metals, 2022, 32(4): 994-1003.

[18] ZHANG J Q, DI H S, WANG X Y. Flow Softening of 253MA Austenitic Stainless Steel during Hot Compression at Higher Strain Rates[J]. Materials Science and Engineering A, 2015, 650: 483-491.

[19] 厉勇, 王春旭, 刘宪民, 等. SAE9310钢奥氏体的冷却转变行为[J]. 机械工程材料, 2010, 34(5): 12-15.

LI Y, WANG C X, LIU X M, et al. Microstructure Transformation Behaviour of Austenite Cooling for SAE9310 Steel[J]. Materials for Mechanical Engineering, 2010, 34(5): 12-15.

[20] 杨雨童, 程晓农, 罗锐, 等. 304和304L奥氏体不锈钢的热加工性能研究[J]. 塑性工程学报, 2019, 26(1): 156-161.

YANG Y T, CHENG X N, LUO R, et al. Research on Hot Workability of 304 and 304L Austenitic Stainless Steel[J]. Journal of Plasticity Engineering, 2019, 26(1): 156-161.

[21] 张一帆, 朱晓飞, 周舸, 等. A100钢的热变形行为及加工图[J]. 精密成形工程, 2022, 14(2): 88-94.

ZHANG Y F, ZHU X F, ZHOU G, et al. Hot Deformation Behavior and Processing Map of A100 Steel[J]. Journal of Netshape Forming Engineering, 2022, 14(2): 88-94.

[22] CORTES C, VAPNIK V. Support-Vector Networks[J]. Machine Learning, 1995, 20(3): 273-297.

[23] KHALAJ G, NAZARI A, YOOZBASHIZADEH H, et al. Retracted Article: ANN Model to Predict the Effects of Composition and Heat Treatment Parameters on Transformation Start Temperature of Microalloyed Steels[J]. Neural Computing and Applications, 2014, 24(2): 301- 308.

[24] MAHESH R, DHANYA S. Modelling the Hardened Properties of Steel Fiber Reinforced Concrete Using ANN[J]. Materials Today: Proceedings, 2022, 49(P5): 2081-2089.

[25] 徐显强, 董显娟, 徐勇, 等. 7050铝合金蠕变本构模型及其泛化能力研究[J]. 精密成形工程, 2023, 15(7): 96-103.

XU X Q, DONG X J, XU Y, et al. Creep Constitutive Model and Generalization Ability of 7050 Aluminum Alloy[J]. Journal of Netshape Forming Engineering, 2023, 15(7): 96-103.

[26] WU S W, ZHOU X G, CAO G M, et al. The Improvement on Constitutive Modeling of Nb-Ti Micro Alloyed Steel by Using Intelligent Algorithms[J]. Materials & Design, 2017, 116: 676-685.

9310 Steel Constitutive Model Optimization Based on Artificial Neural Network Intelligent Algorithm

SHI Wenpeng1, SUN Cenhua1, LI Jiajun2, WANG Yuhang2, DONG Xianjuan2

(1. Jiangxi Jinghang Aviation Forging & Casting Co., Ltd., Jiangxi Jingdezhen 330046, China; 2. School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)

The work aims to study the thermal deformation behavior of 9310 steel under the conditions of deformation temperature of 800-1200 ℃, strain rate of 0.01-50s−1and high depression of 70%, and to establish a constitutive model of 9310 steel with a relatively good prediction effect. An isothermal constant strain rate thermal compression test was carried out on 9310 steel using Gleeble-3800 thermal simulator, and the influence of strain rate on the flow softening effect of 9310 steel was analyzed based on the thermal compression experimental data, and an Arrhenius constitutive model and a support vector regression (SVR) constitutive model considering strain compensation were established, and the model accuracy was analyzed. Compared with the deformation temperature, the strain rate had a more significant effect on the flow softening effect of 9310 steel. Compared with the Support Vector Regression (SVR) constitutive model, the Arrhenius constitutive model considering strain compensation had higher accuracy, with a correlation coefficientof 0.9934, an average relative error (AARE) and a mean square error (MSE) of 0.0556 and 89.362, respectively, and a high strain rate (1, 10, 50s−1).After the optimization of the ANN intelligent algorithm, the correlation coefficientwas increased to 0.9991, the AARE and MSE were reduced to 0.0199 and 9.998, respectively. The proportion of the predicted flow stress with an absolute error of ±10MPa was 98.34%. The softening effect is stronger at low strain rate (0.01s−1). The degree of recrystallization is lower at high strain rate (10s−1), and the softening effect is weaker. The Arrhenius constitutive model optimized by ANN intelligent algorithm has high accuracy and can accurately predict the flow behavior of 9310 steel.

9310 steel; constitutive model; Arrhenius constitutive model; artificial neural network (ANN); intelligent algorithm optimization

10.3969/j.issn.1674-6457.2024.03.019

TG142.1+4

1674-6457(2024)03-0171-10

2024-01-05

江西省自然科学基金面上项目（20232BAB204050）

Natural Science Foundation of Jiangxi Province (20232BAB204050)

施文鹏, 孙岑花, 李佳俊, 等. 基于人工神经网络智能算法的9310钢本构模型优化[J]. 精密成形工程, 2024, 16(3): 171-180.

SHI Wenpeng, SUN Cenhua, LI Jiajun, et al. 9310 Steel Constitutive Model Optimization Based on Artificial Neural Network Intelligent Algorithm[J]. Journal of Netshape Forming Engineering, 2024, 16(3): 171-180.