解析Poly6-I屈服准则对3104-H19铝合金拉深制耳预测的研究
2024-03-20胡启陈军
胡启,陈军
解析Poly6-I屈服准则对3104-H19铝合金拉深制耳预测的研究
胡启*,陈军
(上海交通大学 塑性成形技术与装备研究院,上海 200030)
研究解析Poly6-I屈服准则预测具有高各向异性的3104-H19铝合金本构关系的能力,并将其应用于有限元仿真分析中,以实现对3104-H19铝合金拉深制耳的精确预测。分析解析Poly6-I屈服准则的表达形式,减少计算参数所需的试验个数,并与经典的Yld2004-18p屈服准则进行对比,验证它对高各向异性力学性能预测的能力,将其嵌入到有限元软件中进行杯型件拉深制耳模拟,验证模型的精确性和有效性。对于高各向异性材料,解析Poly6-I屈服准则所使用的试验个数可以减少到11,它预测的3104-H19铝合金屈服轨迹的各向异性系数曲线和单向拉伸曲线与Yld2004-18p屈服准则预测的结果基本相同,杯型件拉深有限元模拟结果与试验结果基本一致。与Yld2004-18p屈服准则相比,考虑高各向异性特性的解析Poly6-I屈服准则所使用的试验数据更少,且无须使用优化软件求取参数,更为方便。解析Poly6-I屈服准则能精确地预测3104-H19铝合金材料在杯型件拉深试验中的制耳个数及杯型件杯壁的成形高度。
屈服准则;解析;拉深;数值仿真;制耳
在碳中和大背景下,轻量化是节能减排的一种重要手段。铝合金作为一种有效的轻量化材料,其密度仅为钢铁材料密度的1/3。铝合金材料具有质量轻、价格便宜、耐腐蚀等特点,被广泛用于汽车行业和航空航天领域。在汽车领域,相关研究表明,在不降低各零部件性能的前提下,采用铝合金替代传统钢铁材料大约可以减重30%[1-5]。但经过轧制工艺生产的铝合金板料往往表现出明显的各向异性,为了改进成形工艺以及避免产品缺陷,需要选择合适的本构模型来预测铝合金的流变行为[6-9]。
随着塑性理论的不断发展,出现了大量的各向异性本构模型[10-14]。相比于传统的使用优化软件求参的屈服准则,近几年许多学者提出了各种无须求参的解析型屈服准则[15-22]。但是这些新提出的解析型屈服准则大都还只使用了材料的力学特性进行验证。对实际零件成形的有限元模拟预测,特别是对高各向异性的铝合金材料变形特性的预测还很少。因此,十分有必要进一步通过有限元模拟来验证这些屈服准则的有效性。
对于验证屈服准则是否适用于高各向异性的铝合金,使用杯型件拉深制耳试验是一种很好的验证方式。过去几十年,研究人员通过大量试验总结出了板料拉深制耳与各向异性系数之间的关系[23-25]。比如当Δ=(0−245+90)/2>0(0、45和90分别为沿轧制方向、与轧制方向呈45°方向和横截面方向的各向异性系数)时,制耳位于轧制方向和横截面方向。当Δ<0时,制耳靠近与轧制方向成45°的方向。但对于高各向异性的铝合金材料,如2090-T3和3104铝合金,以上经验公式的预测结果往往与试验结果相差甚远[11,26]。为此,很多学者提出了一些高阶屈服函数来描述铝合金复杂的力学特性,并成功预测了6个制耳和8个制耳[11,17,26]。
本文通过比较Hu等[18]提出的解析Poly6-I屈服准则与Yld2004-18p屈服准则,并将其用于预测3104-H19铝合金的高各向异性力学性能及杯型件拉深制耳高度,验证了解析Poly6-I屈服准则的精确性和有效性。同时明确了对于高各向异性铝合金材料,该屈服准则中参数最少的试验数据。
1 解析Poly6-I屈服准则
在平面应力状态下,本文所选择的解析Poly6-I屈服准则的表达式如式(1)所示。
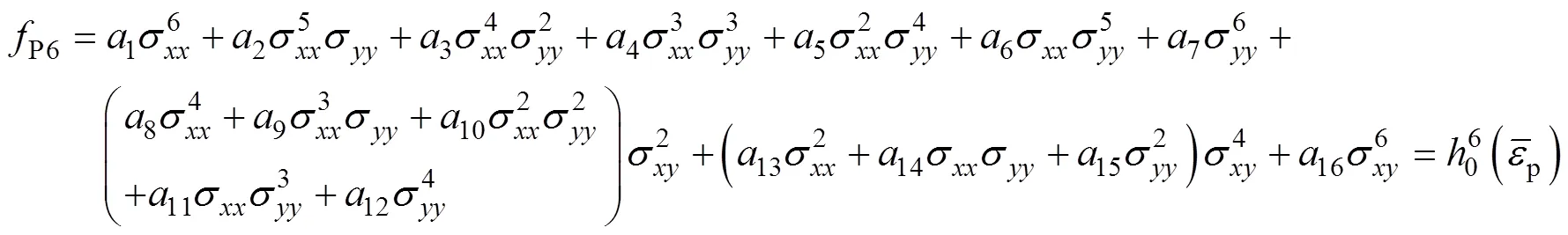
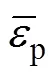
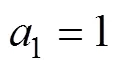
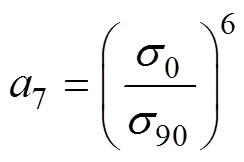
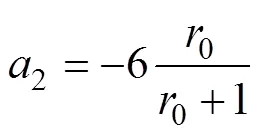
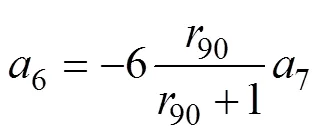
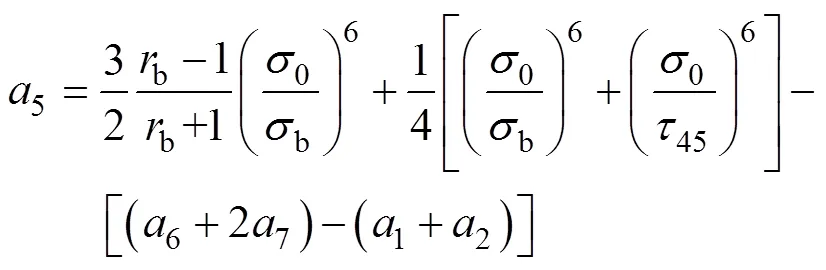
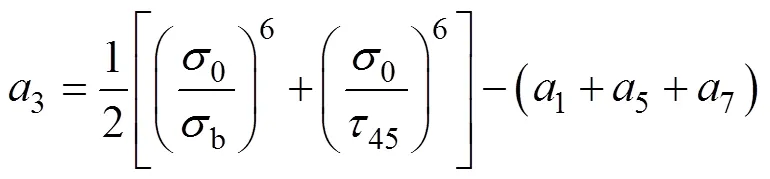
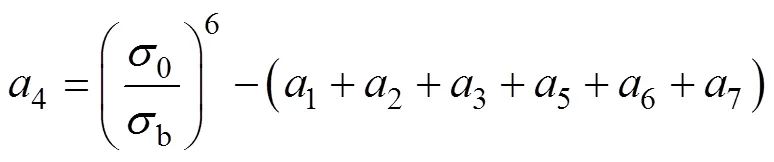
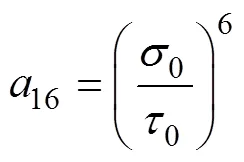
式中:0、45、90、b分别为沿轧制方向、对角线方向(与轧制方向呈45°方向)、横截面方向和等双拉状态下的各向异性系数;0、45,90、b分别为沿轧制方向、对角线方向(与轧制方向呈45°方向)、横截面方向和等双拉状态下的屈服应力;0和45分别为纯剪切状态下沿轧制方向和对角线方向的屈服应力。式(1)中参数8~15的表达式如式(10)~(20)所示。
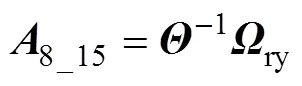
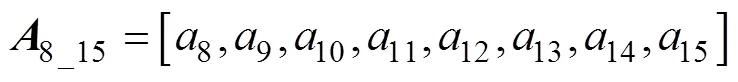
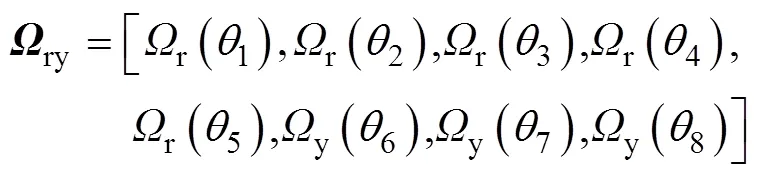

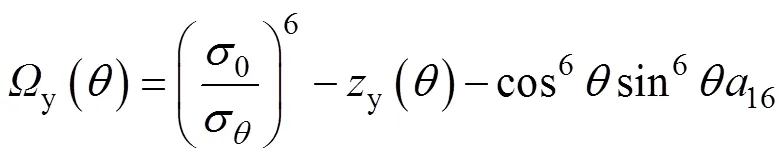

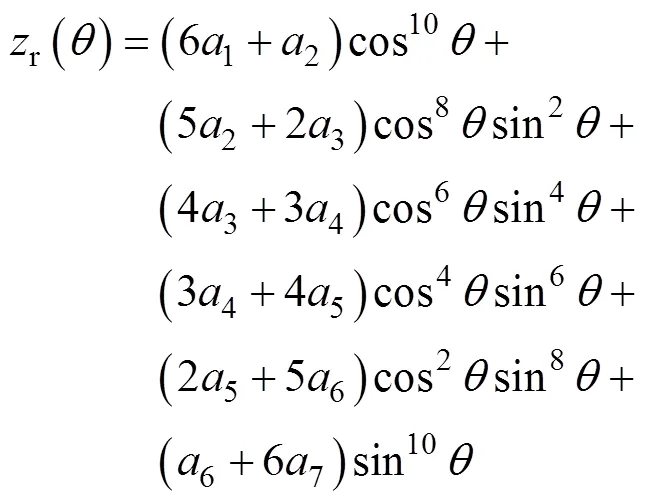
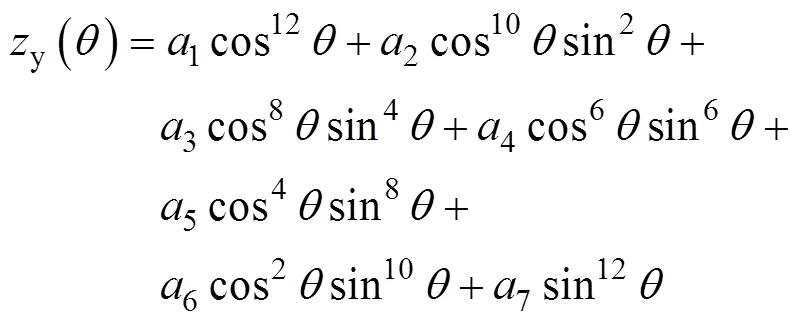

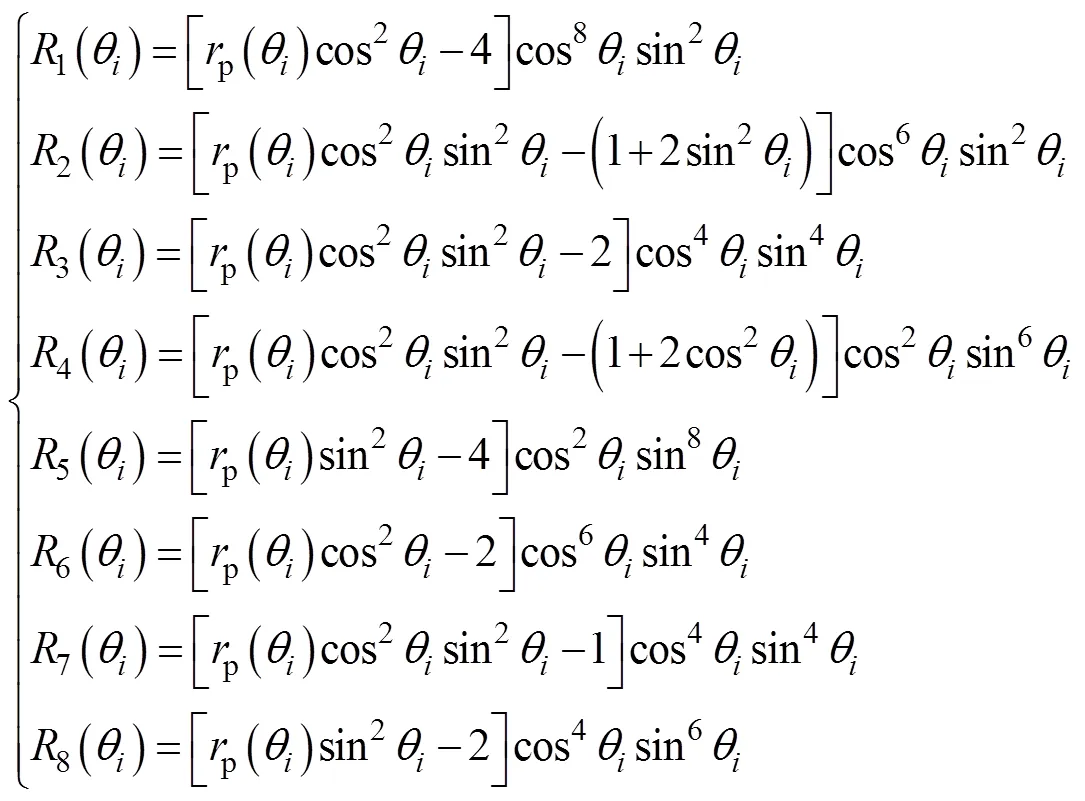

式中:1~8为8个单向拉伸与轧制方向的角度;为单向拉伸方向与轧制方向的夹角;σ和r为相应的屈服应力和各向异性系数;θ为单向拉伸方向与轧制方向的夹角。计算参数8~15时将会使用除了0、45、90、0、45、90以外的6个单拉数据(15、30、60、75、22.5、67.5)。
如式(1)所示,虽然该屈服准则有16个参数,但这并不意味着需要使用16个试验数据。减少试验个数将使该屈服准则的使用变得更加方便。对于高各向异性的铝合金材料,其各向异性系数曲线最多会产生2个波峰或者波谷(不考虑0和90处的状态)。因此除了使用0、45、90外还需要选择2个值。根据文献[12],可以使用22.5和67.5。为了尽量减少试验数据,将采用由解析Hill48屈服准则(如式(21)所示)计算得到的屈服应力15、30、60、75以及试验得到的22.5、67.5来计算参数8~15,即将式(12)中的变量θ(=1~8)分别取π/8、π/4、3π/8、π/12、π/6、π/4、π/3和5π/12。
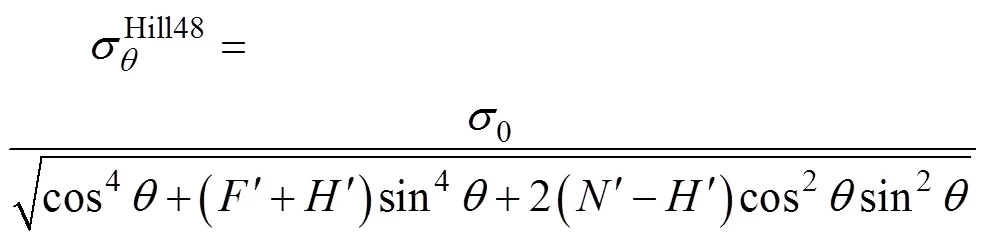
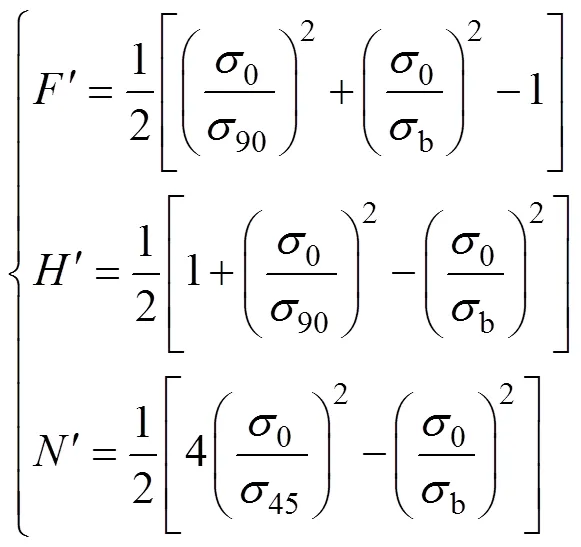
2 高各向异性3104-H19铝合金的力学特性
为了验证解析Poly6-I屈服准则预测复杂各向异性行为的能力,选取了具有高各向异性特性的3104-H19铝合金[26]。选用如式(23)所示的Swift硬化模型拟合该材料沿轧制方向的单向拉伸流动曲线的拟合参数如下:=331.46 MPa,0=0.000 18和=0.050 13,其他力学属性如表1所示。
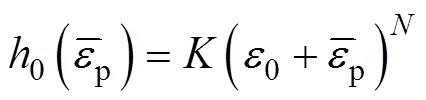
式中:、0和为Swift硬化模型中的参数。
表1 3104-H19铝合金的力学属性
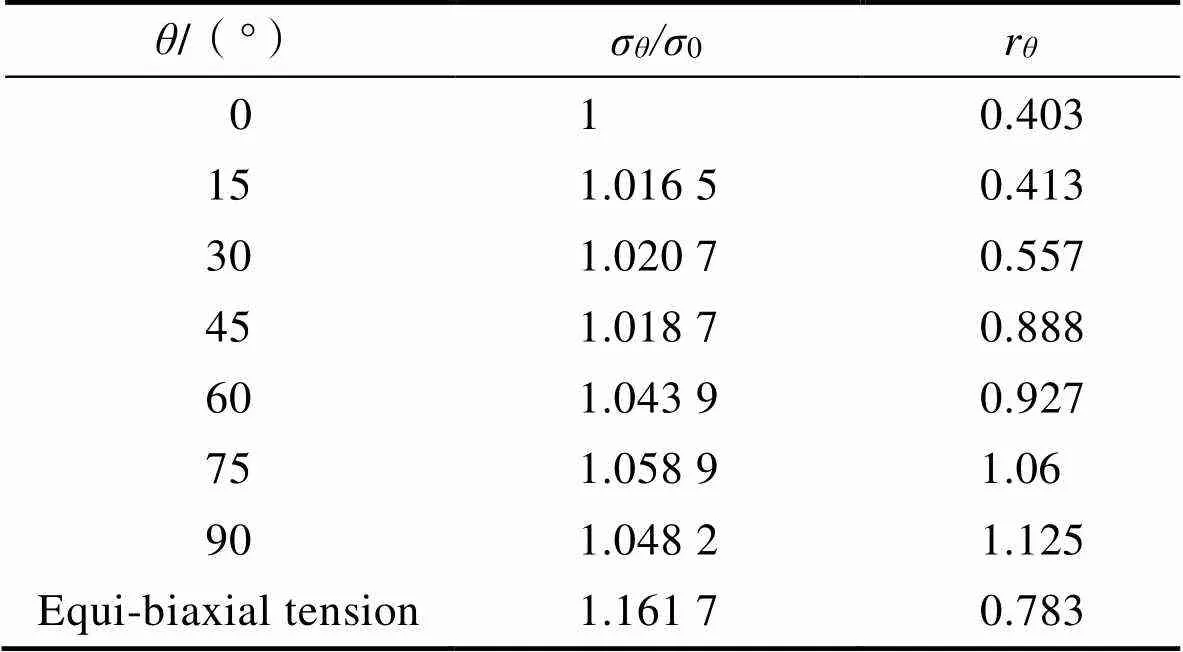
Tab.1 Mechanical properties of 3104-H19 aluminum alloy
对于沿轧制方向和沿45°方向的纯剪切应力0和45,将采用解析Poly4*Hosford屈服准则[17,19]来计算,如式(24)所示。
(24)
式中:为指数参数;1¢~5¢为参数,其表达式如式(25)~(29)所示。
(25)
(26)
(27)
(28)
(29)
综上所述,对于解析Poly6-I屈服准则,所需要使用的试验数据为0、45、90、b、0、45、90、b、22.5、67.5以及45(或指数)。
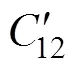
表2 对于3104-H19铝合金材料Yld2004-18p (=8)的参数

Tab.2 Parameters of Yld2004-18p (m=8) for 3104-H19 aluminum alloy
由于缺乏45这个试验数据,因此将通过其他屈服准则计算获得。通过Yld2004-18p屈服准则可以计算得到45=0.623 4。对于式(24),当指数=5时,所计算的45=0.624。对于3104-H19铝合金,将使用式(24)来计算0和45。此外由于缺乏22.5和67.5这2个试验数据,因此将采用22.5=(15+30)/2和67.5=(60+75)/2计算得到。解析Poly6-I屈服准则和Yld2004-18p屈服准则预测的归一化屈服轨迹如图1所示。可以看到,它们预测的屈服轨迹基本上是重合的。这2个屈服准则预测的不同单拉方向上的各向异性系数以及归一化屈服应力如图2所示。所预测的屈服应力曲线基本上是一样的。对于各向异性系数曲线,由于解析Poly6-I屈服准则是采用试验数据直接解析计算参数,所以它可以精确地穿过每一个使用的数据点。而对于Yld2004-18p屈服准则,由于它需要使用优化算法来求解参数,并不能很好地预测每一个试验数据点。这是因为在平面应力状态下,Yld2004-18p屈服准则有如表2所示的14个参数,但是在优化参数的过程中,使用到了如表1所示的16个试验数据。而对于解析Poly6-I屈服准则,除了使用0、45、90外,所使用的另外2个值22.5和67.5能很好地控制曲线的变化规律。
总体来说,对于3104-H19铝合金,解析Poly6-I屈服准则预测屈服轨迹、单拉应力曲线和曲线的能力与Yld2004-18p屈服准则基本相当。但解析Poly6-I屈服准则只需要11个试验数据点,而Yld2004-18p则需要14个试验数据点,且解析Poly6-I屈服准则中的参数是解析表达的,无须采用复杂的方式优化求解。解析屈服准则的参数是唯一的,并不会依赖求参软件的优化函数和权重系数。因此,解析Poly6-I屈服准则更为准确,使用也更加方便。
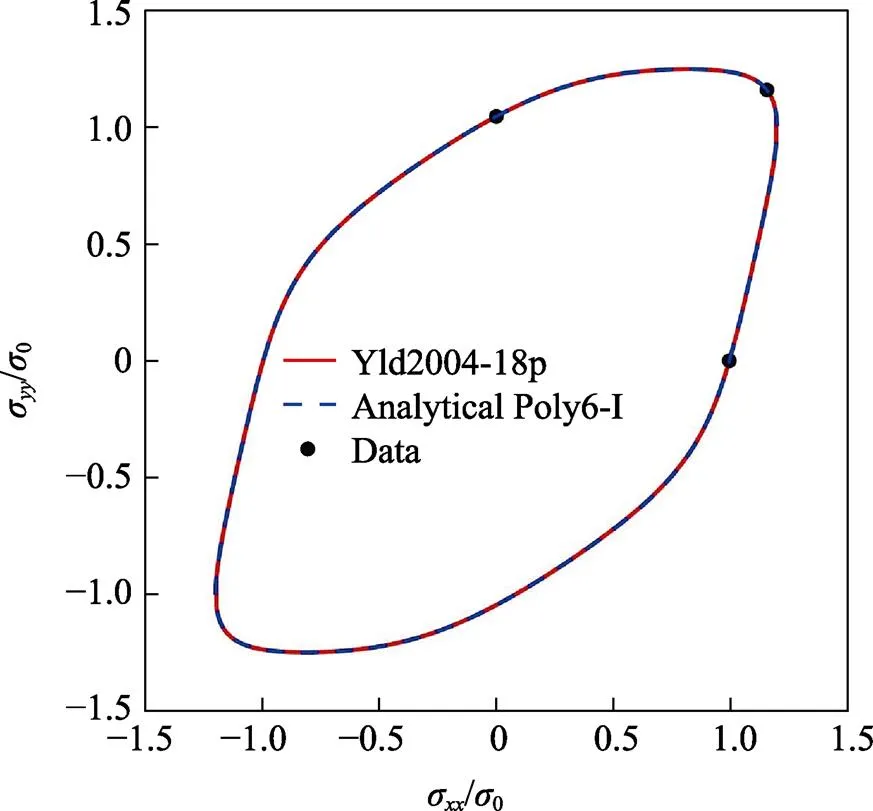
图1 不同屈服准则预测的归一化屈服轨迹
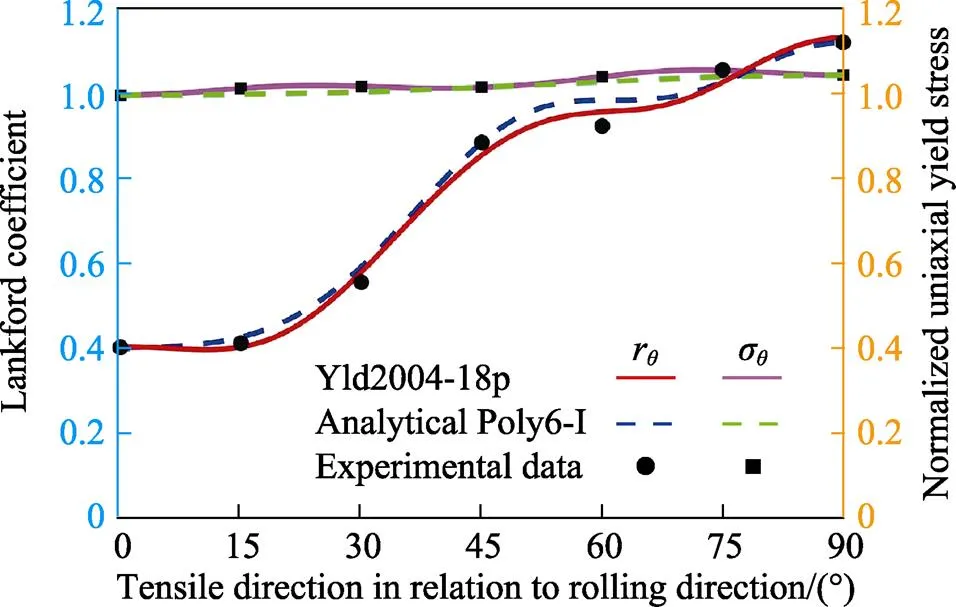
图2 不同屈服准则预测的各向异性系数和归一化屈服应力
3 杯型件拉深制耳预测
3.1 杯型件拉深试验和数值模拟
杯型件拉深制耳是一种验证屈服准则对高各向异性材料是否适用的有效试验方法。本文将采用文献[26]中的杯型件拉深试验,试验模具尺寸如图3所示。试验材料为厚度0.274 mm的3104-H19铝合金。试样几何形状为直径76.12 mm的圆形。该拉深试验是在最大载荷为5 t的液压机中进行的。在拉深过程中,冲头的恒定行程速度为140 mm/s,压边力恒定为8.9 kN,冲头行程为25 mm。在试验过程中,为了减小坯料与模具之间的摩擦,在试样上下表面涂抹了一层润滑油。试验所获得的杯型拉深件形貌如图4所示。
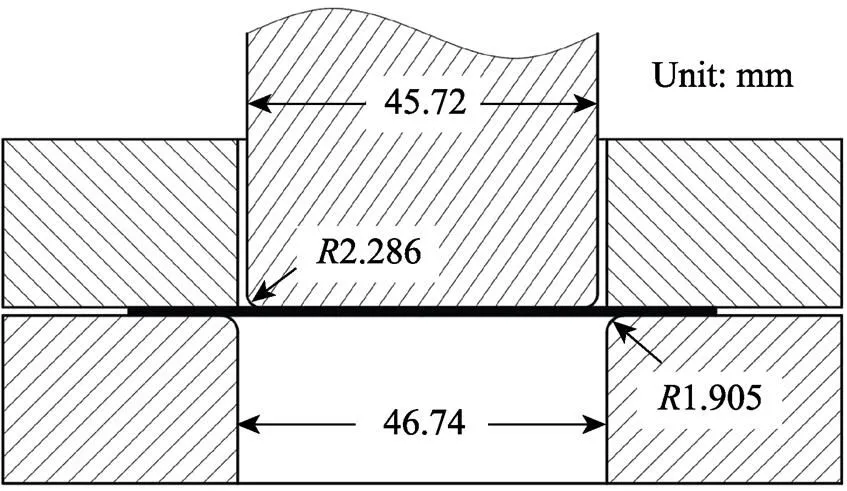
图3 杯型件拉深试验示意图

图4 3104-H19铝合金杯形件拉深轮廓形貌[26]
为了使用有限元软件精确模拟杯型件拉深试验,采用差分法将解析Poly6-I屈服准则嵌入ABAQUS/ Standard中。考虑到材料的对称性,在有限元模型设置中只选取了1/4部分进行模拟。选择壳单元S4R,单元尺寸为1.0 mm,厚向积分点设为5,板料与压边圈、凹模和冲头的摩擦因数设为0.045,压边力设置为8.9 kN。解析Poly6-I屈服准则预测的杯型件拉深形貌如图5所示。可以看到,它与试验结果非常相似。
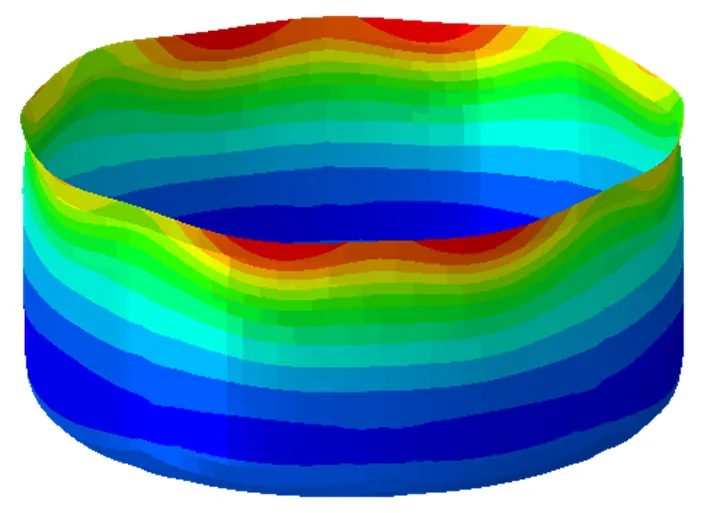
图5 解析Poly6-I屈服准则预测3104-H19铝合金的杯形轮廓形貌
3.2 制耳高度模拟结果
为了直观验证解析Poly6-I屈服准则预测3104-H9铝合金的制耳能力,比较了不同角度处的杯壁高度,如图6所示。可知,在0°~20°、160°~200°以及340°~360°区间,解析Poly6-I屈服准则预测的制耳精度要稍微优于Yld2004-18p的。而在其他区域,Yld2004-18p屈服准则预测的杯壁高度要比解析Poly6-I屈服准则所预测的更高一些,且更接近试验数据。由文献[27]可知,杯型件制耳高度主要与各向异性系数r+90相关。如图2和图7所示,这2个屈服准则所预测的各向异性系数曲线有些许差异。由图7可知,在沿轧制方向70°~90°内,解析Poly6-I屈服准则预测的值更加准确,这也是解析Poly6-I屈服准则预测的杯壁高度在0°~20°、160°~200°以及340°~ 360°区间更准确的原因。
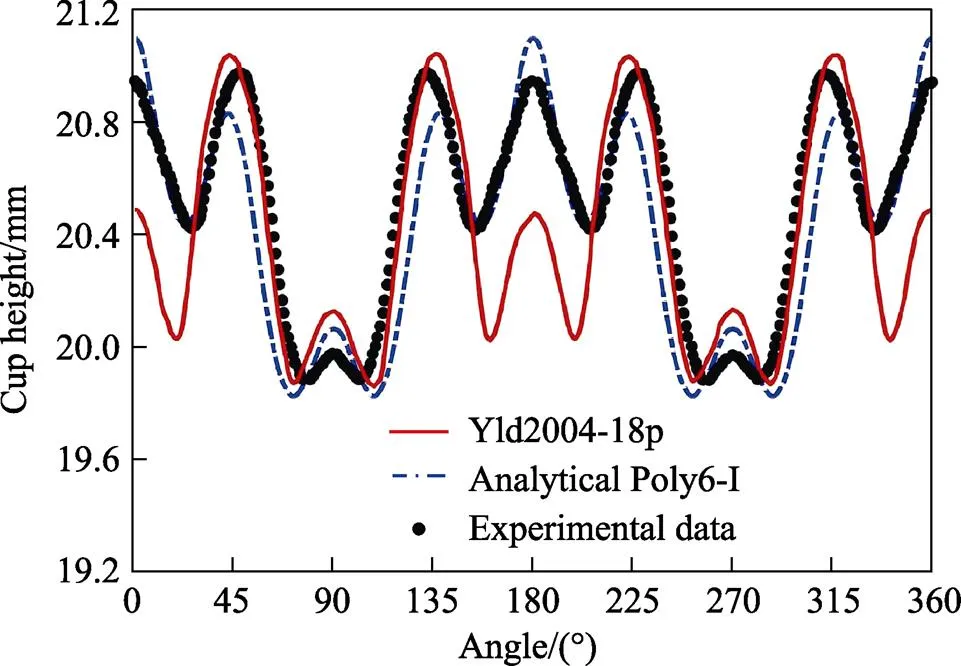
图6 不同屈服准则预测的杯壁高度

图7 不同屈服准则预测r值相对误差绝对值
总体来说,如图1和图2所示,解析Poly6-I屈服准则和Yld2004-18p屈服准则所预测的屈服轨迹、各向异性系数曲线和单向拉伸曲线与试验数据都非常接近,因此它们所预测的杯壁高度基本一样,且都能准确地预测3104-H19铝合金的制耳个数和杯型件高度。
4 结论
提出了简化解析Poly6-I屈服准则参数的计算策略,并与Yld2004-18p屈服准则进行了对比,将它们应用到杯型件拉深制耳的预测中,得到以下结论:
1)解析Poly6-I屈服准则预测的屈服轨迹、单拉应力曲线和曲线的能力与Yld2004-18p屈服准则的能力相当。考虑高各向异性特性的解析Poly6-I屈服准则只需要使用11个试验数据,且无须使用优化软件求取参数,更为方便。
2)解析Poly6-I屈服准则能精确地预测3104-H19铝合金材料在杯型件拉深试验中的制耳个数及杯型件杯壁的成形高度。
[1] 汪文芳, 孙成武. 汽车铝合金开发与应用[J]. 汽车实用技术, 2018(18): 258-259.
WANG W F, SUN C W. Development and Application of Automobile Aluminum Alloy[J]. Automobile Applied Technology, 2018(18): 258-259.
[2] 林才渊, 初冠南, 林艳丽. 6063铝合金中空构件充液压形成形[J]. 塑性工程学报, 2018, 25(4): 46-52.
LIN C Y, CHU G N, LIN Y L. Low-Pressure Hydroforming for 6063 Aluminum Alloy Hollow Component[J]. Journal of Plasticity Engineering, 2018, 25(4): 46-52.
[3] 胡志力, 芦俊杰, 华林. 铝合金热冲压技术研究进展[J]. 锻压技术, 2022, 47(2): 1-11.
HU Z L, LU J J, HUA L. Review of Hot Stamping Technology for Aluminum Alloy[J]. Forging & Stamping Technology, 2022, 47(2): 1-11.
[4] 周彬, 王成, 汪森辉, 等. 基于GTN和CDM的5754铝合金板材成形极限曲线和失效行为对比分析[J]. 塑性工程学报, 2023, 30(10): 135-143.
ZHOU B, WANG C, WANG S H, et al. Comparison Analysis of Forming Limit Curves and Failure Behaviors of 5754 Aluminum Alloy Sheet Metal Based on GTN and CDM[J]. Journal of Plasticity Engineering, 2023, 30(10): 135-143.
[5] 王国军. 轻量化汽车用铝合金板材结构设计及应用技术研究进展[J]. 轻合金加工技术, 2022, 50(4): 1-13.
WANG G J. Research Progress in Structure Design and Application Technology of Lightweight Automobile Aluminum Alloy Sheet[J]. Light Alloy Fabrication Technology, 2022, 50(4): 1-13.
[6] 周兵营, 豆远航, 吴向东, 等. TA4纯钛带材各向异性屈服行为表征与研究[J]. 精密成形工程, 2023, 15(2): 11-18.
ZHOU B Y, DOU Y H, WU X D, et al. Characterization and Study on Anisotropic Yield Behavior of TA4 Pure Titanium Strip[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 11-18.
[7] 黄珍媛, 谭朋朋, 魏婉珠, 等. 3104铝合金薄板本构模型[J]. 塑性工程学报, 2021, 28(7): 117-123.
HUANG Z Y, TAN P P, WEI W Z, et al. Constitutive Model of 3104 Aluminum Alloy Sheet[J]. Journal of Plasticity Engineering, 2021, 28(7): 117-123.
[8] 方刚, 陈祝, 雷丽萍. 非关联本构模型在铝合金板料成形有限元模拟中的应用[J]. 塑性工程学报, 2021, 28(6): 8-18.
FANG G, CHEN Z, LEI L P. Application of Non-Associated Constitutive Models in Finite Element Simulation of Aluminum Alloy Sheet Forming[J]. Journal of Plasticity Engineering, 2021, 28(6): 8-18.
[9] 付健, 郭丽丽. 本构方程对6016铝合金板材成形极限影响分析[J]. 大连交通大学学报, 2019, 40(3): 97-101.
FU J, GUO L L. Effect of Constitutive Equation on Forming Limit of 6016 Aluminum Alloy[J]. Journal of Dalian Jiaotong University, 2019, 40(3): 97-101.
[10] BARLAT F, BREM J, YOON J, et al. Plane Stress Yield Function for Aluminum Alloy Sheets-Part 1: Theory[J]. International Journal of Plasticity, 2003, 19(9): 1297- 1319.
[11] BARLAT F, ARETZ H, YOON J W, et al. Linear Transformation-Based Anisotropic Yield Functions[J]. International Journal of Plasticity, 2005, 21(5): 1009-1039.
[12] YOSHIDA F, HAMASAKI H, UEMORI T. A User-Friendly 3D Yield Function to Describe Anisotropy of Steel Sheets[J]. International Journal of Plasticity, 2013, 45(7): 119-139.
[13] LOU Y, HUH H, YOON J W. Consideration of Strength Differential Effect in Sheet Metals with Symmetric Yield Functions[J]. International Journal of Mechanical Sciences, 2013, 66: 214-223.
[14] MIN J, CARSLEY J E, LIN J, et al. A Non-quadratic Constitutive Model under Non-associated Flow Rule of Sheet Metals with Anisotropic Hardening: Modeling and Experimental Validation[J]. International Journal of Mechanical Sciences, 2016, 119: 343-359.
[15] STOUGHTON T, YOON J. Anisotropic Hardening and Non-Associated Flow in Proportional Loading of Sheet Metals[J]. International Journal of Plasticity, 2009, 25(9): 1777-1817.
[16] LEE E H, STOUGHTON T, YOON J. A Yield Criterion through Coupling of Quadratic and Non-Quadratic Functions for Anisotropic Hardening with Non- Associated Flow Rule[J]. International Journal of Plasticity, 2017, 99: 120-143.
[17] HU Q, YOON J, MANOPULO N, et al. A Coupled Yield Criterion for Anisotropic Hardening with Analytical Description under Associated Flow Rule: Modeling and Validation[J]. International Journal of Plasticity, 2021, 136: 102882.
[18] HU Q, YOON J W, STOUGHTON T B. Analytical Determination of Anisotropic Parameters for Poly6 Yield Function[J]. International Journal of Mechanical Sciences, 2021, 201: 106467.
[19] HU Q, YOON J W, CHEN J. Analytically Described Polynomial Yield Criterion by Considering Both Plane Strain and Pure Shear States[J]. International Journal of Plasticity, 2023: 103514.
[20] HOU Y, MIN J Y, STOUGHTON T, et al. A Non-Quadratic Pressure-Sensitive Constitutive Model under Non-Associated Flow Rule with Anisotropic Hardening: Modeling and Validation[J]. International Journal of Plasticity, 2020, 135(1): 102808.
[21] HU Q, YOON J. Analytical Description of an Asymmetric Yield Function (Yoon2014) by Considering Anisotropic Hardening under Non-Associated Flow Rule[J]. International Journal of Plasticity, 2021, 140: 102978.
[22] LOU Y S, YOON J. Lode-Dependent Anisotropic-Asymmetric Yield Function for Isotropic and Anisotropic Hardening of Pressure-Insensitive Materials. Part I: Quadratic Function under Non-Associated Flow Rule[J]. International Journal of Plasticity, 2023, 166: 103647.
[23] 吴青松, 祝洪川, 王立新, 等. 塑性应变比各向异性度与制耳率之间关系探讨[J]. 物理测试, 2013, 31(1): 14-16.
WU Q S, ZHU H C, WANG L X, et al. Relationship between Degree of Planar Anisotropy and Earing Ratio[J]. Physics Examination and Testing, 2013, 31(1): 14-16.
[24] 肖华, 石磊, 仝广, 等. 冲压成形凸耳不均匀的产生及影响因素[J]. 锻压技术, 2009, 34(3): 53-56.
XIAO H, SHI L, TONG G, et al. Influencing Factors on Unequal Earing Stamping[J]. Forging & Stamping Technology, 2009, 34(3): 53-56.
[25] 林艳丽, 何祝斌, 袁杭, 等. 金属板材拉深制耳形状与各向异性系数的解析关系模型[J]. 塑性工程学报, 2021, 28(6): 19-25.
LIN Y L, HE Z B, YUAN H, et al. Analytical Relationship Model of Ear Profile and Anisotropy Coefficient of Sheet Metal Deep Drawing[J]. Journal of Plasticity Engineering, 2021, 28(6): 19-25.
[26] DICK R E, YOON J W. Plastic Anisotropy and Failure in Thin Metal: Material Characterization and Fracture Prediction with an Advanced Constitutive Model and Polar EPS (Effective Plastic Strain) Fracture Diagram for AA 3014-H19[J]. International Journal of Solids and Structures, 2018, 151: 195-213.
[27] YOON J, BARLAT F, DICK R, et al. Prediction of Six or Eight Ears in a Drawn Cup Based on a New Anisotropic Yield Function[J]. International Journal of Plasticity, 2006, 22(1): 174-193.
Earing Prediction by Analytical Poly6-I Yield Criterion on 3104-H19 after Deep Drawing
HU Qi*, CHEN Jun
(Institute of Forming Technology & Equipment, Shanghai Jiao Tong University, Shanghai 200030, China)
The work aims to study the constitutive relationship of the high anisotropic material 3104-H19 aluminum alloy predicted by the analytical Poly6-I yield criterion, and implement it into the finite element simulation analysis to accurately predict the earing of 3104-H19 aluminum alloy after deep drawing. Through analyzing the expression of analytical Poly6-I yield criterion, the number of tests required to calculate the parameters was reduced. Compared with the classical Yld2004-18p yield criterion, its ability to predict high anisotropy characteristics was verified, and it was implemented into the finite element software to simulate the earing for cup deep drawing, which was used to verify the accuracy and effectiveness of the model. For high anisotropic material, the number of tests used for Poly6-I yield criterion could be reduced to 11, and the predicted yield locus, Lankford coefficient curve and uniaxial tension curve of 3104-H19 aluminum alloy were almost the same as those predicted by the Yld2004-18p yield criterion, and the result of the finite element simulation of cup drawing was consistent with the experiments. Compared with the Yld2004-18p yield criterion, the analytical Poly6-I yield criterion uses less experimental data and does not use optimization software to obtain parameters, which is more user-friendly. The analytical Poly6-I yield criterion can accurately predict the number of ears and the height of the cup wall for 3104-H19 aluminum alloy after cup deep drawing.
yield criterion; analytical; drawing; numerical simulation; earing
10.3969/j.issn.1674-6457.2024.03.014
TG386.2
A
1674-6457(2024)03-0138-07
2023-12-22
2023-12-22
上海市浦江人才计划;国家自然科学基金(92160206)
Sponsored by Shanghai Pujiang Program; The National Natural Science Foundation of China (92160206)
胡启, 陈军. 解析Poly6-I屈服准则对3104-H19铝合金拉深制耳预测的研究[J]. 精密成形工程, 2024, 16(3): 138-144.
HU Qi, CHEN Jun. Earing Prediction by Analytical Poly6-I Yield Criterion on 3104-H19 after Deep Drawing[J]. Journal of Netshape Forming Engineering, 2024, 16(3): 138-144.
(Corresponding author)
