基于准连续域束缚态的全介质超构表面双参数传感器*

刘会刚 张翔宇 南雪莹 赵二刚 刘海涛4)5)

1) (南开大学,薄膜光电子技术教育部工程研究中心,天津 300350)

2) (南开大学电子信息与光学工程学院,微电子工程系,天津 300350)

3) (南开大学电子信息与光学工程学院,电子信息实验教学中心,天津 300350)

4) (南开大学电子信息与光学工程学院,现代光学研究所,天津 300350)

5) (天津市微尺度光学信息技术科学重点实验室,天津 300350)

本文设计了由不对称半圆柱对阵列组成的全介质超构表面,获得了两个高品质因子的准连续域束缚态模式(quasi-bound states in the continuum,QBIC).通过选择不同形式的对称破缺,在近红外频段均可产生两个稳健的QBIC,并且二者的谐振波长、品质因子、偏振依赖等表现出不同的特性.模拟计算表明,通过测量两个QBIC 的谐振波长,能够实现折射率和温度的双参数传感;通过调节不对称参数,利用QBIC 的品质因子依赖于不对称参数的二次方反比关系,理论上能够提高品质因子到任意的数值,从而实现传感性能的提升和调节.该超构表面的折射率传感灵敏度、品质因子和优值分别达到194.7 nm/RIU,45829 和8197,其温度传感灵敏度达到24 pm/℃.

1 引言

基于超构表面的高灵敏传感技术是目前光学传感领域的一个研究热点.现有超构表面的损耗包括辐射损耗和材料损耗.目前,材料损耗可以通过全介质材料替代金属材料的方式大幅度减弱,于是辐射损耗成为限制光与物质相互作用强度的主要因素.近期研究表明,通过改进微纳加工技术以及调整辐射场分布可以抑制辐射损耗,其中连续域束缚态(bound states in the continuum,BICs)是减弱全介质超构表面的辐射损耗以获取高品质因子共振的有效手段[1].BICs 的概念起源于量子力学,1929 年由冯⋅诺依曼和威格纳[2]以薛定谔方程为基础引入,目前已经在波动物理学领域得到深入研究.BIC 定义为共振频率位于辐射模式的连续频率范围内,但是具有无限寿命的、场完全局域的束缚模式.BIC 模式本征频率的虚部γ=0(本征频率为复数ω=ω0-iγ,定义为波动方程的本征值,其中实部ω0是谐振频率,虚部γ表示衰减速率),品质因子Q=ω0/(2γ)趋于无穷大,被认为是具有零泄漏和零线宽的理想共振模式,有时被称为“陷阱模式”或“暗模式”[3].2008年,BIC 的概念首次在光学领域被讨论[4];2011年,Plotnik 等[5]通过实验证明了二维波导阵列结构中光学BIC 模式的存在,成为BIC 概念提出后的第一个实验证明.此后,光子晶体纳米薄板[6,7]、光波导阵列[8,9]、超构表面[10–12]等各种光学结构相继通过BIC 实现了高Q因子共振.BIC 模式是理想化的状态,这种非辐射的暗模式只有与外部辐射相互耦合转换为具有超窄线宽的泄漏模式,即准BIC (quasi-BIC,QBIC)模式,对于增强光与物质相互作用才具有现实意义[13].具有较高品质因子的QBIC 模式在高灵敏传感[14]、量子光学[15]、非线性增强[16]、低损耗激光器[17]等方面具有重要应用.

光学BIC 模式产生的基本机制是谐振模式与周围空间中所有辐射模式之间的解耦合,可以根据解耦合的物理起源分为两类[1,18].一类是由于参数的连续调节导致意外解耦合的束缚模式,可以称为“偶然型BIC”.一个或多个系统参数的连续调节,使得暗模式与辐射模式的耦合意外消失,形成具有无限Q因子的偶然型BIC,这种BIC 模式在调节参数时会保证系统的对称性[13].另一类是由于空间对称(镜像或旋转对称)导致离散模式和连续辐射模式解耦合的束缚模式,称为“对称保护型BIC”.此类BIC 很不稳定,会在不对称参数的调控下转变为具有极高Q因子的QBIC 共振模式,其优点是可控性较高.2016年,Liu 等[19]设计了不对称双圆孔阵列结构,该结构产生的Fano 共振的线宽会随着双圆孔半径差值的减小逐渐变窄,半径差值为1 nm 时对应的Q因子高达2.4×106,但是结构完全对称时共振消失.2017年,Sun 等[20]利用不对称翻转双硅条阵列,也发现了类似的高品质因子共振,两个开缝的硅条长度差值为0.1 nm时,对应的Q因子约为108.2018年,Koshele 等[13]针对具有不同面内反转对称元胞的全介质超构表面,借助对称保护型BIC 理论,对产生的高品质因子法诺共振现象进行了统一的解释,严格证明了QBIC 与法诺共振之间的联系,并借助并矢格林函数推导出了QBIC 的Q因子反比于不对称参数的二次方.2019年,Mikheeva 等[21]使用光敏硫族化合物As2S3制成由两个矩形棒阵列组成的超构表面传感器,通过控制两个矩形棒的“长度差”打破面内对称性,并由不对称参数α 表征不对称程度,模拟了透射率对波长和α 的依赖关系,当α 从零逐渐增大时,具有无限大Q因子的对称保护型BIC演变为具有有限大Q因子的QBIC.同年,Wang 等[22]设计了周期性不对称纳米棒二聚体组成的全介质超构表面折射率传感器,成对的硅纳米棒阵列被放置在二氧化硅衬底上,可以通过控制二聚体的“厚度差”实现多个具有较窄线宽和较大调制深度的Fano 共振,其中最大的Q因子超过9700,最大的优值FOM 达到5045.2020年,Chen 和Fan[10]提出一种由单层石墨烯、LiTaO3裂隙双矩形条阵列、铁电相变材料钛酸锶薄膜构成的太赫兹超构表面,通过改变矩形条长度的差值∆L=L1–L2打破面内对称,可以激发尖锐的QBIC 法诺共振.

由于对称保护型BIC 的易调谐性,其对称破缺产生的具有高Q因子的QBIC 吸引了众多学者的关注.然而,现有研究大多基于单个BIC 和单一对称破缺形式,对于多个BIC 以及多种对称破缺形式的研究较少,且鲜有研究者研究其用于折射率和温度的双参数传感.如果能形成多个BIC,并采用多种对称破缺形式获得相应的QBIC,则有望拓展器件性能调控的参数空间,以及获得更丰富和优异的传感性能.本文针对基于BIC 的折射率和温度双参数传感器开展了研究,设计了可以支持双QBIC 共振的不对称半圆柱对全介质超构表面,突破了常规的单个QBIC 共振的局限.本文设计的超构表面通过破坏结构的对称性,在透射率光谱中得到了两种由对称保护型BIC 产生的QBIC 共振;通过控制不对称参数的数值,能够灵活地控制QBIC 模式的谱线宽度,理论上能够提高品质因子到任意的数值,从而实现传感性能的提升和调节.本征模式分析表明,面内和面外对称破缺产生的共振模式的Q因子均反比于不对称参数的二次方,从而证实了这些共振模式属于QBIC[13];分析了不同对称破缺形式对QBIC 模式的影响.模拟计算表明,通过测量两个QBIC 的谐振波长,能够实现折射率和温度的双参数传感,其折射率传感灵敏度S达到194.7 nm/RIU,品质因子Q达到45829,优值FOM 达到8197,其温度传感灵敏度达到24 pm/℃.

2 对称全介质超构表面透射率谱与谐振特性分析

2.1 超构表面结构参数

本文设计的对称破缺全介质超构表面双参数传感器,结构示意图如图1 所示.该超构表面由平铺在玻璃基底上的成对的硅半圆柱阵列组成,半圆的圆心如图1(b)单元晶胞中的黑色圆点所示,圆点连线平行于x轴,并且连线中点为单元晶胞的中心.定义坐标原点O位于玻璃基底表面和单元晶胞的中心.沿x,y方向阵列周期px=py=600 nm,两个半圆柱的半径和厚度分别为r1=225 nm,d1=50 nm和r2,d2,半圆柱上、下部分的缝宽分别为s2和s1=30 nm.设置三种不对称参数α=s2-s1,β=r1-r2,γ=d2-d1,其中缝宽差α使得结构关于y=0 不对称,半径差β 或厚度差γ使得结构关于x=0 不对称,α,β 描述了面内(即x-y平面内)的对称破缺程度,厚度差γ描述了面外(即沿z轴方向)的对称破缺程度.玻璃基底的折射率为1.5,硅的折射率为3.5,该阵列浸入折射率n=1.312 的水溶液中,平面波沿负z轴方向入射.

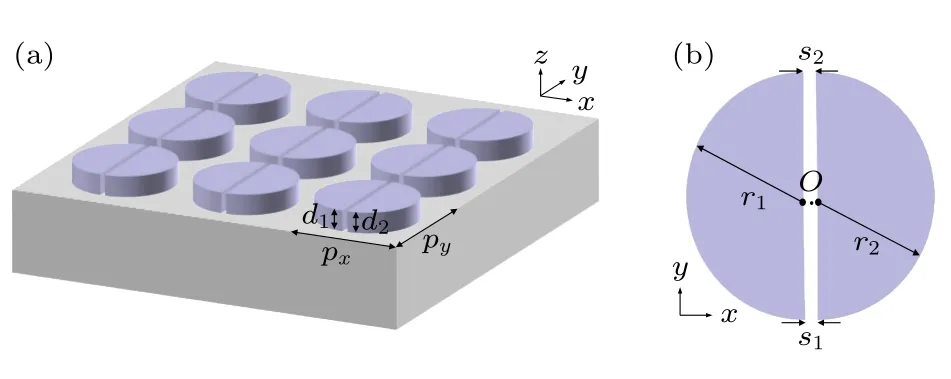
图1 (a) 半圆柱对全介质超构表面示意图;(b) 单元晶胞俯视图Fig.1.(a) Schematic diagram of the all-dielectric metasurface composed of semicircular cylinder pairs;(b) top view of a unit cell.

2.2 对称超构表面透射率谱与谐振特性

首先针对上述超构表面的对称结构进行数值分析,即令α=β=γ=0.使用商用多物理场软件COMSOL Multiphysics 的RF 模块进行模拟仿真,得到对称结构的透射率谱线如图2 所示.可见x向偏振光入射时,透射率谱在907.53 nm 处出现谐振极小值,该谐振模式记为Mx;y向偏振光入射时,透射率谱在919.88 nm 处出现谐振极小值,该谐振模式记为My.

图2 对称 超构表面的 透射率谱,红色实线对 应x 向偏振光入射,蓝色实线对应y 向偏振光入射.图中4 个圆圈表示4 个QNM 本征模式复数本征波长的实部,红色、绿色、蓝色和紫色圆圈对应的QNM 分别记为Mx,BIC2,My,BIC1Fig.2.Transmission spectrum of the symmetric metasurface.Red solid line corresponds to the incidence of x-polarized light,the blue solid line corresponds to the incidence of y-polarized light.Circles in the figure represent the real part of the complex eigenwavelengths of the four QNM eigenmodes,and the QNMs corresponding to the red,green,blue and purple circles are denoted as Mx,BIC2,My and BIC1,respectively.

谐振模式(或本征模式)可以严格定义为准简正模式(quasinormal mode,QNM)[20],QNM 为谐振结构无源Maxwell 方程组的本征解,其电磁场在无穷远处满足外行波边界条件,对应一个复数本征频率ωm=+.由于谐振结构存在散射损耗或吸收损耗,使得复数本征频率的虚部<0(对应时间因子exp(–iωt)).QNM 的品质因子定义为Q=/(-) .使用COMSOL 软件RF 模块中的本征模式求解器,可以求解得到QNM 的复数本征频率和电磁场分布.在透射率谱中,Q=λ0/FWHM,其中λ0为共振波长,FWHM 为透射率谱谐振峰的半高全宽.因此,Q因子越高(即越接近0),则FWHM 越小,谐振峰越尖锐.

对于上述对称超构表面,可以在考虑的频带内求解得到4 个QNM,对应的复数本征频率分别是ωm/(2π)=3.0341×1014Hz,(3.2678×1014—2.0285×1012i) Hz,3.2795×1014Hz,(3.3139×1014—2.1464×1012i) Hz (设依次对应m=1,2,3,4).需要注意,COMSOL 软件RF 模块中的本征模式求解器选取的时间因子为exp(iωt),相应地,求解得到的ωm满足>0 .因此,对应本文时间因子exp(–iωt),COMSOL 软件求解得到的ωm应取复数共轭,使得满足<0.ωm对应的复数本征波长(即λm=2πc/ωm,c为真空中光速)的实部Re(λm) 用圆圈标记在图2 中.在红色圆圈和蓝色圆圈对应的波长处,COMSOL 本征模式求解器得到的2 个QNM的电磁场分布与RF 模块得到的实数频率下的电磁场分布类似,因此,前文提到的Mx和My模式即可严格定义为这2 个QNM.另外,在图2 紫色圆圈和绿色圆圈对应的波长处,还存在2 个=0的QNM,其品质因子Q为无穷大,此即BIC 模式,分别记为BIC1 和BIC2.

为了深入了解对称超构表面的谐振特性,BIC1和BIC2 的电磁场分布图如图3(a)—(d)所示.由x-y水平截面图可知,BIC1 的电场主要分布在缝隙中,磁场主要集中在半圆柱圆心附近.BIC2 的电场主要分布在缝隙中以及半圆柱的周围,磁场则主要集中在半圆柱边缘.由y-z垂直截面图可知,两个BIC 模式的电场和磁场均被束缚在超构表面附近,只有较少的能量分布在衬底和水溶液中.可见,BIC1 和BIC2 的电磁场分布存在明显差异,反映出二者形成的物理机制不同.为了研究对称破缺对透射率谱的影响,下文将通过引入三种不同形式的对称破缺进行分析,通过引入不对称参数α 和β 打破超构表面的面内对称性,通过引入不对称参数γ打破超构表面的面外对称性.

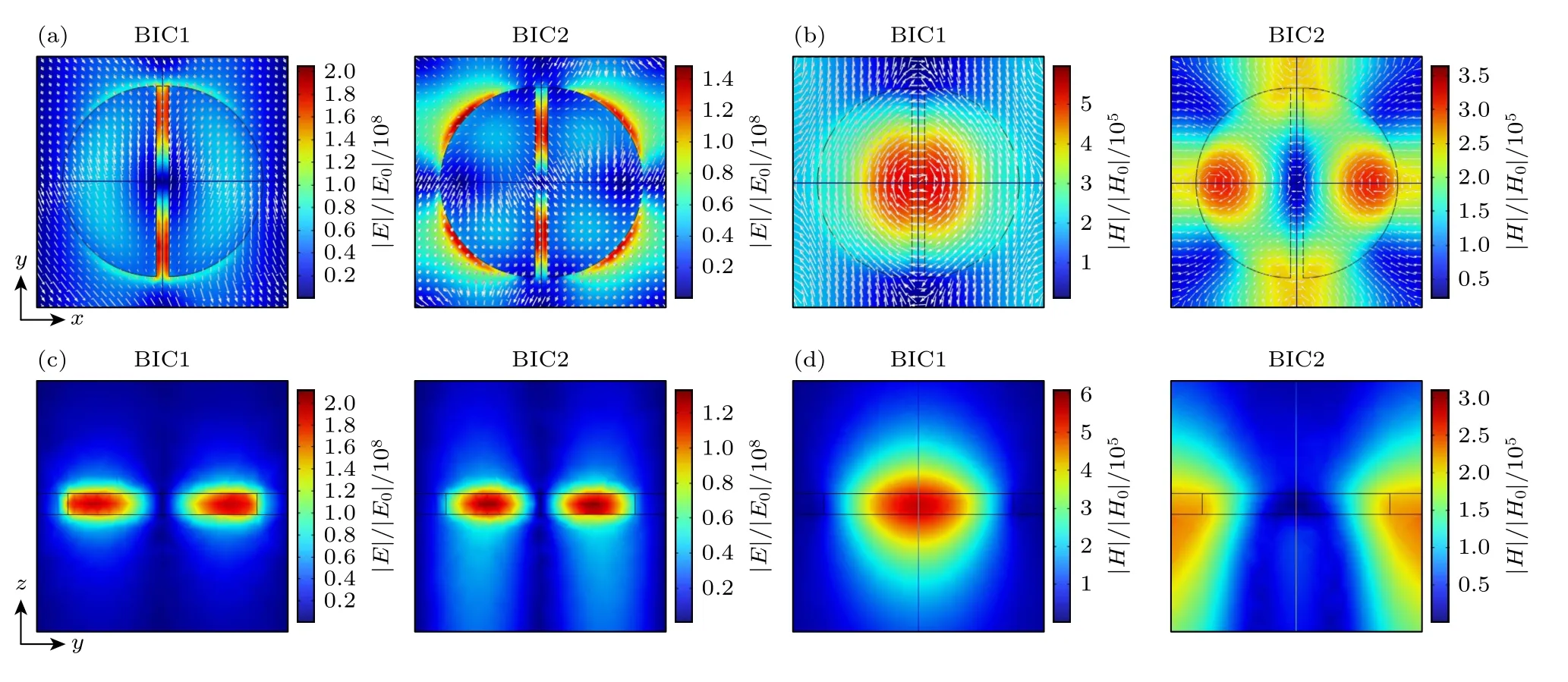
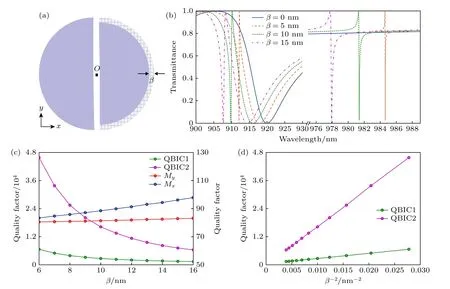
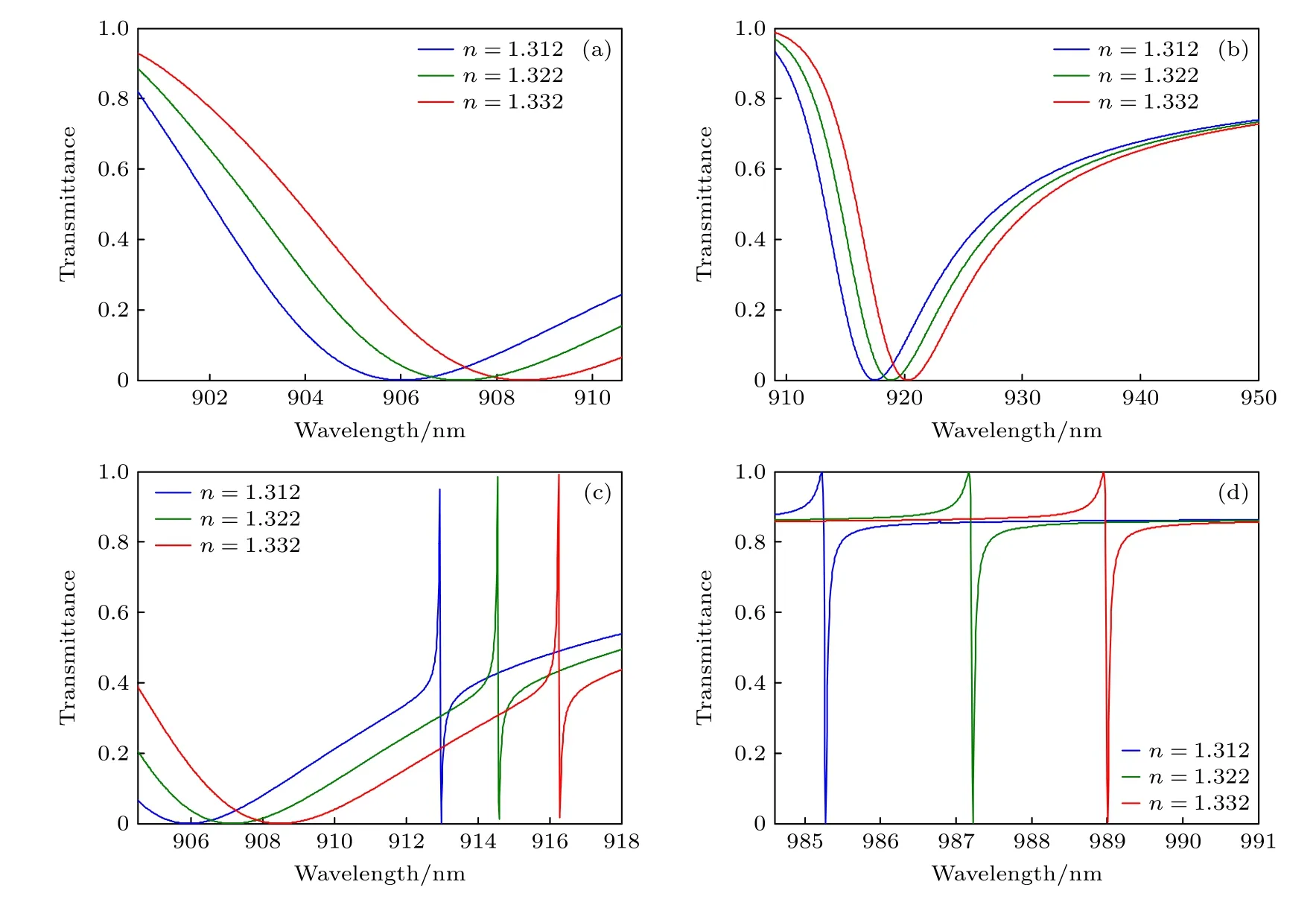
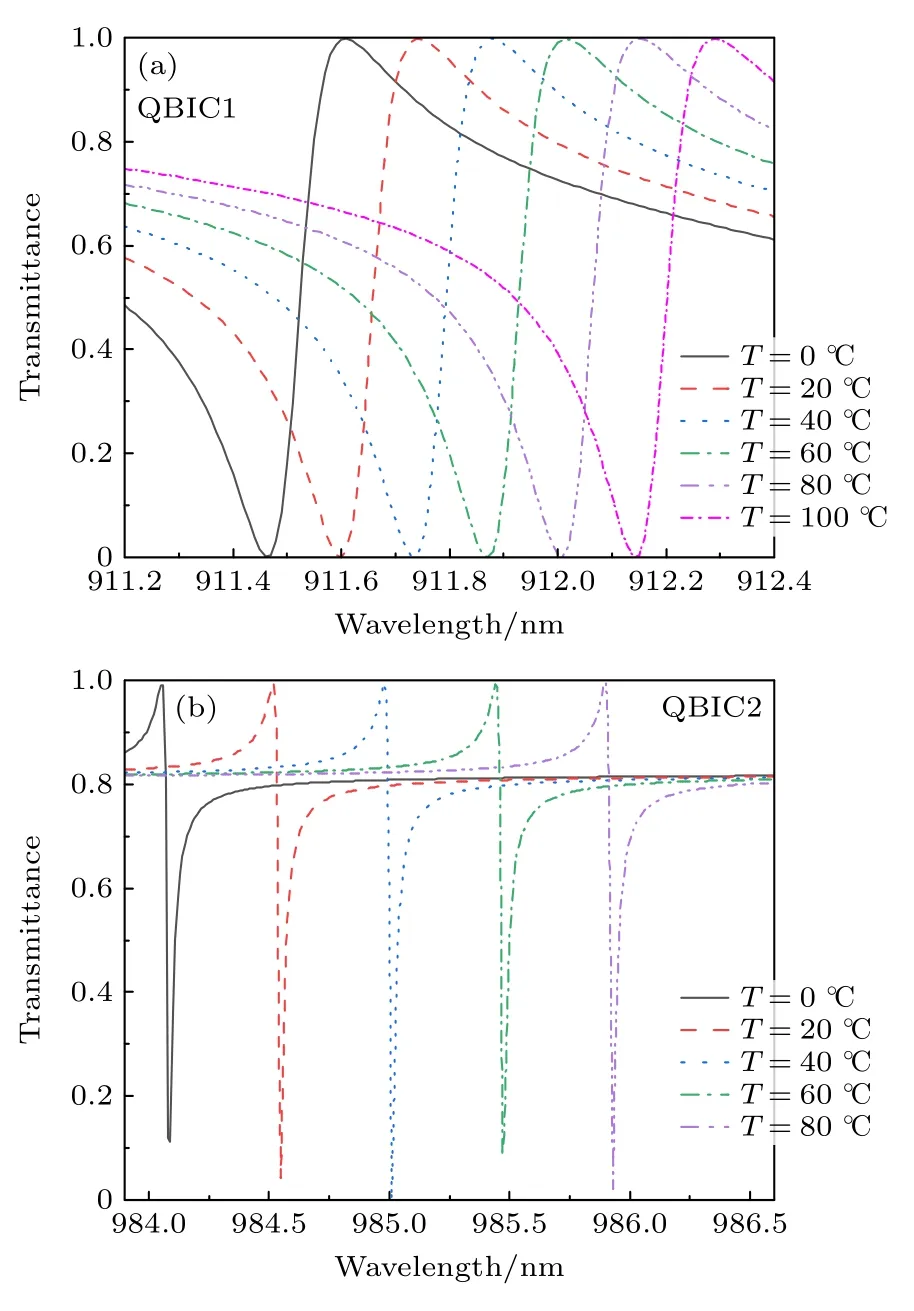
图3 (a) 两种BIC 模式在x-y 平面(z=d1,z

3 对称破缺全介质超构表面透射率谱分析与双参数传感应用

3.1 面内对称破缺超构表面透射率谱

图4(a)是通过引入对称半圆柱上下部分的缝宽差异(不对称参数α)实现面内对称破缺的结构示意图,此时固定不对称参数β=γ=0.α 取值不同时,仿真得到超构表面的透射率谱线如图4(b)所 示.α=s2-s10时,x向偏振 光入射时,Mx模式的右侧出现了2 个尖锐的不对称谱型的Fano 共振峰,随着不对称参数α 的逐渐减小,这两个Fano 共振的峰值波长红移并且线宽逐渐变窄.例如,α=5 nm时,x向偏振光入射对应的透射光谱中,Mx右侧的两个尖锐Fano 共振谷值分别位于913.36 nm 和986.34 nm.这2 个Fano 共振模式和前文BIC 模式的电磁场分布相似,由此推断,这2 个Fano 共振模式为QBIC 模式,记为QBIC1 和QBIC2 (分别对应前文BIC1 和BIC2).当α=0时,两个Fano 共振同时消失,即有限Q因子的QBIC1 和QBIC2 转变为无穷大Q因子的BIC1 和BIC2[13].当α ≠ 0时,y向偏振光入射对应的透射率谱与对称结构(α=0)类似,无QBIC 模式出现,My的谐振波长与对称结构相比存在蓝移现象.

图4 (a) 面内不对称参数 α=s2-s10 时全介质超构表面示意图;(b) 不对称参数α 不同时,x 向偏振光入射对应的透射率谱线;(c) 不对称参数α 不同时,四个本征模式的Q 因子变化曲线;(d) QBIC1 和QBIC2 的Q 因子随1/α2 的变化曲线Fig.4.(a) Schematic diagram of the all-dielectric metasurface when the in-plane asymmetric parameter α=s2-s10 ;(b) transmittance spectra for x-polarized incident light and different asymmetric parameters α;(c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter α;(d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/α2.

图4(c)展示了不对称参数α 取值不同时,透射光谱中四个谐振模式Mx,My,QBIC1 和QBIC2的Q因子的变化曲线.由图4(c)可知,Mx和My的Q因子受不对称参数α 的影响较小,而QBIC1和QBIC2 的Q因子随着不对称参数α 的减小迅速增大.如图4(d)所示,对于较小的不对称参数α,QBIC1 和QBIC2 的Q因子对α 的依赖关系遵循二次方反比关系,从而证实了QBIC1 和QBIC2均属于QBIC 模式[13].例如当α=8 nm时,QBIC1和QBIC2 的Q因子分别达到30125 和28097.因此,可以通过控制不对称参数α,调控QBIC1 和QBIC2 的品质因子.当不对称参数α 取不同数值时,BIC1,BIC2 (α=0 nm)或QBIC1,QBIC2 (α=20,40 nm)的磁场振幅分布如图5 所示,可以观察到随着不对称参数α 的减小,电磁场越来越局域,这也是品质因子增大的一个表现.

图5 (a) α=0 nm,(b) α=20 nm,(c) α=40 nm 时BIC1(或QBIC1)在平面x=0 内的磁场振幅分布;(d) α=0 nm,(e) α=20 nm,(f) α=40 nm 时BIC2 (或QBIC2)在平面x=0 内的磁场振幅分布.图中叠加的黑色实线显示了结构的边界,H0 表示入射平面波的磁场矢量Fig.5.Distributions of magnetic-field amplitude for BIC1 (or QBIC1) in plane x=0 when (a) α=0 nm,(b) α=20 nm,(c) α=40 nm,and distributions of magnetic-field amplitude for BIC2 (or QBIC2) in plane x=0 when (d) α=0 nm,(e) α=20 nm,(f) α=40 nm.The superimposed black solid lines show the boundary of the structure.The H0 represents the magnetic-field vector of the incident plane wave.

除了上述引入缝宽差异打破超构表面的面内对称性之外,还可以通过引入两个半圆柱半径的差异(即不对称参数β=r1–r2≠ 0)实现面内对称破缺的效果,如图6(a)所示,此时固定不对称参数α=γ=0.半径差值β 变化时超构表面的透射率谱如图6(b)所示.在β 减小至0 的过程中,x偏振光入射时透射率谱的谐振模式与对称结构(β=0)类似,无QBIC 模式出现,并且Mx模式的谐振波长与对称结构相比存在红移现象.当y偏振光入射时,透射率谱出现了两个QBIC 模式(对应两个尖锐的透过率谷);与前述α≠0 不同的是,β≠0时,这两个QBIC 模式位于My模式的两侧.图6(c)展示了透射光谱中四个本征模式的Q因子随不对称参数β 的演变.可以看出,在不对称参数β 减小的过程中,Mx和My的Q因子变化缓慢,而QBIC1 和QBIC2 的Q因子迅速增大.如图6(d)所示,当β 较小时,QBIC1 和QBIC2 的Q因子对β 的依赖关系同样遵循二次方反比关系,从而证实了QBIC1 和QBIC2 均属于QBIC 模式[13].例如当β=6 nm时,QBIC1 和QBIC2 的Q因子分别为45829 和6639.

图6 (a) 面内不对称参数 β=r1-r20 β=r1–r2 ≠ 0 时全介质超构表面示意图;(b) 不对称参数β 不同时,y 向偏振光入射对应的透射率谱;(c) 不对称参数β 不同时,四个本征模式的Q 因子变化曲线;(d) QBIC1 和QBIC2 的Q 因子随1/β2 的变化曲线Fig.6.(a) Schematic diagram of the all-dielectric metasurface when the in-plane asymmetric parameter β=r1-r20 ;(b) transmittance spectra for y-polarized incident light and different asymmetric parameters β;(c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter β;(d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/β2.

3.2 面外对称破缺超构表面透射率谱

除了上述2 种面内对称破缺的调控方法之外,该超构表面也可在面外对称破缺的调控下产生高Q因子的QBIC 共振,面外对称性的打破可以通过两个半圆柱厚度的差异实现(即不对称参数γ=d2–d1≠ 0),此时固定不对称参数α=β=0,不对称结构如图7(a)所示.图7(b)是γ取值不同时对应的透射率谱,γ≠ 0 时透射光谱的变化和引入不对称参数β 导致的透射光谱变化类似:x偏振光入射时,透射光谱中无QBIC 模式出现;y向偏振光入射时,两个QBIC 模式的谐振波长位于My模式谐振波长的两侧.随着不对称参数γ逐渐减小至0,四个模式的谐振波长存在蓝移现象.图7(c)中四个模式的Q因子随不对称参数γ的演化曲线表明,面外不对称性同样能够调节QBIC 模式的Q因子.如图7(d)所示,与面内对称破缺类似,QBIC1,QBIC2 模式的Q因子与不对称参数γ的依赖关系也遵循二次方反比关系,从而证实了QBIC1,QBIC2均属于QBIC 模式[13].例如当γ=2 nm时,QBIC1和QBIC2 的Q因子分别达到41417 和7572.

图7 (a) 面外不对称参数 γ=d2-d10 时全介质超构表面示意图;(b) 不对称参数γ 不同时,y 向偏振光入射对应的透射率谱;(c) 不对称参数γ 不同时,四个本征模式的Q 因子变化曲线;(d) QBIC1 和QBIC2 的Q 因子随1/γ2 的变化曲线Fig.7.(a) Schematic diagram of the all-dielectric metasurface when the out-of-plane asymmetric parameterγ=d2-d10(b) transmittance spectra for y-polarized incident light and different asymmetric parameters γ;(c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter γ;(d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/γ2.

需要说明的是,由于两个BIC 的电磁场分布不同(图3),不同的对称破缺形式产生的QBIC 也有不同.引入缝宽差不对称参数α时,对两个QBIC模式的影响类似,由图4(d)可以看出,两个QBIC模式的Q因子比较接近,这是由于两个BIC 模式在狭缝中均有较强的电场分布(图3).但是当引入半径差不对称参数β 或厚度差不对称参数γ时,由图6(d)和图7(d)可以看出,两个QBIC 模式的Q因子差异较大,这是由于在圆柱边缘,BIC1 电场较弱,而BIC2 电场较强(图3).

3.1 节和3.2 节的分析表明,通过引入面内(不对称参数α≠0 或β≠0)或面外(γ≠ 0)对称破缺,当特定偏振光入射时(α ≠ 0 时x偏振光入射,β ≠ 0 或γ≠ 0 时y偏振光入射),透射率谱会出现两个QBIC 模式导致的尖锐谐振峰,有利于传感等相关应用(见3.3 节).这些QBIC 模式的Q因子随不对称参数的变化遵循二次方反比的关系,于是可以通过调节不对称参数,任意地控制这些QBIC 模式的Q因子,提高传感等相关应用的性能.但是在传感器的实际加工中,由于加工误差,会限制不对称参数能取的最小的数值,从而会限制品质因子能达到的最高数值.

3.3 对称破缺超构表面折射率和温度双参数传感应用

由BIC 引入对称破缺得到的QBIC 会形成极窄线宽的共振峰,有利于提高传感等相关应用的性能.本文提出的超构表面引入对称破缺后,可以产生两个具有高品质因子和高光谱对比度的QBIC模式,下面研究其作为折射率和温度传感器时的性能.灵敏度S和优值FOM 是衡量传感特性的两个重要指标.对于折射率传感,灵敏度定义为[23]

其中,Tp和Td分别为谐振峰附近透过率的最大值、最小值.对于温度传感,灵敏度定义为[24]

首先,分析对称破缺超构表面的折射率传感性能.设超构表面浸没在折射率n由1.312 到1.332变化的待测水溶液中,环境温度T=25 ℃.后文方程(4)表明,即使环境温度T≠ 25 ℃ (即方程(4)中∆T=T-25 ℃ ≠0),折射率传感灵敏度(对应方程(6)右端矩阵第一列)仍可取为T=25 ℃对应的折射率传感灵敏度.

仅引入不对称参数α=8 nm 时(β=γ=0),设x偏振光入射,待测液体折射率n不同时对应的透射率谱如图8 所示,折射率的增大导致四个模式Mx,My,QBIC1 和QBIC2 的谐振波长均发生红移.表1 给出了不同的不对称参数下四个模式的共振波长、折射率传感灵敏度、Q因子和FOM 的计算结果,初始的待测液体折射率均为1.312,其中β=6 nm (α=γ=0)和γ=2 nm 时(α=β=0),均为y偏振光入射.

表1 不同的不对称参数下四个模式折射率传感的计算结果Table 1.Calculation results of the four modes for refractive-index sensing with different asymmetric parameters.

图8 待测液体折射率n 变化时,不同模式谐振波长附近的透射率谱.设仅引入不对称参数α=8 nm (β=γ=0),x 偏振光入射(a) Mx;(b) My;(c) QBIC2;(d) QBIC1Fig.8.When the refractive index n of the tested liquid changes,the transmittance spectra of different modes.Only the asymmetric parameter α=8 nm (β=γ=0) is introduced,and the incident light is x-polarized: (a) Mx;(b) My;(c) QBIC2;(d) QBIC1.

表1 的数据表明,对于折射率传感,与通常的共振模式Mx,My相比,BIC 引入对称破缺形成的谐振模式QBIC1 和QBIC2 具有更高的传感灵敏度S,以及异常优越的Q因子和FOM 值.此外,QBIC1 和QBIC2 均具有较高的光谱对比度V,例如,α=8 nm 时(β=γ=0),QBIC1 和QBIC2 的V分别达到98.64%,100%.

当考虑硅材料存在本征损耗时,设硅的折射率nSi=3.5+ik,在可见光到近红外波段,k随着入射波长的增大而减小[25].根据麦克斯韦方程组的缩放定理,当结构尺寸与波长等比例放大时,如果折射率不变,则电磁场分布及其决定的电磁响应(例如透射率)保持不变.因此,如果把超表面结构尺寸与波长同时放大为η 倍(η ≥ 1,称为缩放因子),并且k相应地减小,则透射率的变化完全来自k的变化.下面以α=8 nm (β=γ=0)的情形为例.当η=1时,在QBIC1 和QBIC2 谐振波长附近,取硅的折射率虚部为k=2.26×10-3[25],与k=0 相比(见表1),QBIC1 和QBIC2 的共振波长不变,但是Q值分别降为1679 和4347.当η为1.7时,取k=1.5×10-6[25],则QBIC1 和QBIC2的共振波长放大为η=1 时的1.7倍,Q值分别为16755 和31041,其数量级接近k=0 时的数值.当η=3时,取k=2.5×10-9[25],则QBIC1 和QBIC2的共振波长放大为η=1 时的3倍,Q值分别为29567 和29451,接近k=0 时的数值.上述计算中,取待测液体折射率n=1.312,相应的透射率谱如图9(a)所示.上述结果表明,随着结构尺寸与入射波长等比例增大和k相应地减小,谐振波长会等比例增大,同时Q值逐渐增大,由此,可根据工作波长和传感器的性能要求来合理设计传感器.

图9 (a)考虑硅材料损耗,取波长和结构尺寸缩放因子η=1,1.7 和3时,传感器的透射率谱;(b)当两个半圆柱的半径r1=r2=223,225 和227 nm时,传感器的透射率谱.上述计算中,取待测液体折射率n=1.312Fig.9.(a) Transmittance spectra of the sensor with the wavelength and all geometrical sizes scaled by a factor of η=1,1.7 and 3,and with the material loss of silicon being considered;(b) transmittance spectra of the sensor when the two semicircular cylinders’ radii are r1=r2=223,225 and 227 nm.In the calculation,the refractive index of the measured liquid is n=1.312.

此外,考虑加工误差对传感器性能的影响,例如,考虑α=8 nm (β=γ=0),k=0 的情形,假设由于加工误差,两个半圆柱的半径偏离设计值r1=r2=225 nm.取r1=r2=223 nm,则QBIC1和QBIC2 的共振波长分别为983.045 和911.3 nm,Q值分别为28085 和22782.取r1=r2=227 nm,则QBIC1 和QBIC2 的共振波长分别为988.176和914.803 nm,Q值分别为24704 和30492.上述计算中,取待测液体折射率n=1.312,相应的透射率谱如图9(b)所示.上述结果表明,当加工误差导致传感器尺寸略微偏离设计值时,除了共振波长发生少量偏移,传感器的Q值变化不大,这表明传感器性能具有较好的鲁棒性.

接下来,分析对称破缺超构表面的温度传感性能.设环境温度变化范围为0 ℃—100 ℃,超构表面上方水环境折射率n=1.312.后文方程(4)表明,即使n≠1.312 (即方程(4)中∆n=n-1.3120),温度传感灵敏度(对应方程(6)右端矩阵第二列)仍可取为n=1.312 对应的温度传感灵敏度.

当仅引入不对称参数β=6 nm 时(α=γ=0),设y向偏振光入射,超构表面的透射率谱如图10 所示.由于结构尺寸小,热膨胀系数可以忽略不计.利用Si 的热光学系数进行仿真,热光学系数κ 定义为光学材料的折射率n随温度T的变化率,即κ=(n-n0)/(T-T0),其中n0为参考温度T0对应的折射率.对于Si,取κ=1.84×10–4/K[26],T0=25 ℃,n0=3.5.玻璃的热光学系数远小于Si,可近似取为0[9].

图10 不对称参数β=6 nm 时(α=γ=0),不同温度T 下的透射率谱曲线.水溶液折射率n 设置为1.312,y 向偏振光入射Fig.10.Spectral curves of transmittance for different temperatures T and the asymmetric parameter β=6 nm (α=γ=0).The refractive index n of the aqueous solution is set to 1.312,and the incident light is y-polarized.

图11 显示了QBIC1 和QBIC2 的温度传感灵敏度,分别为6.81 pm/℃和23.19 pm/℃,可以看到,谐振波长对温度的依赖关系具有良好的线性特性.同时,也对仅引入α=8 nm 或γ=2 nm 时QBIC1 和QBIC2 的温度传感灵敏度进行了计算.α=8 nm,x向偏振光入射时,QBIC1 和QBIC2 的温度传感灵敏度分别为7.27 和23.19 pm/℃;γ=2 nm,y向偏振光入射时QBIC1 和QBIC2 的温度传感灵敏度分别为7.77 和24 pm/℃.

经过计算分析可知,如表2 所列,当仅引入不对称参数α 或β 产生的两个QBIC 模式应用于温度传感时,随着α 或β 不断减小,温度传感灵敏度缓慢提高;在仅引入不对称参数γ时,随着γ不断减小,温度传感灵敏度缓慢降低.

当超构表面上方被测水溶液的折射率和环境温度同时发生变化时,通过测量两个QBIC 模式的共振波长,利用共振波长对折射率和温度的线性依赖关系,可以实现对折射率和温度的双参数传感,从而有效避免折射率和温度之间的串扰.

对于折射率和温度双参数传感器,共振波长的变化量表达为

其中,∆λ1和∆λ2分别代表QBIC1 和QBIC2 的共振波长变化量;∆n和∆T分别代表折射率和温度的变化量.A为传感灵敏度矩阵,定义为

其中,元素AI1,AT1分别代表QBIC1 对应的折射率传感灵敏度和温度传感灵敏度;AI2,AT2分别代表QBIC2 对应的折射率传感灵敏度和温度传感灵敏度,以β=6 nm 为例,其数值已经由前文计算得到:

根据方程(4),折射率和温度的变化量能够表达为

利用方程(7),即可在测量得到∆λ1和∆λ2后,计算得到∆n和∆T,从而实现折射率和温度的双参数传感.需要注意,应用方程(7)的前提是要求矩阵A为可逆矩阵,这等价于要求矩阵A的第1 行、第2 行线性无关,其反映的是共振波长对折射率和温度的依赖关系对于QBIC1 和QBIC2 呈现不同的规律.

接下来,验证对称破缺超构表面能够同时测量环境的折射率和温度.本文分别展示了三种对称破缺下,15 组随机数据的计算结果,如表3 所列.其中∆nset和∆Tmat为预先设定的环境折射率和温度的变化量,∆λ1和∆λ2为环境折射率和温度变化引起的QBIC1 和QBIC2 谐振波长的变化量,∆ncal和∆Ta为矩阵理论方程(7)预测得到的环境折射率和温度的变化量,δn和δT分别为环境折射率和温度传感的相对误差,定义为δn=(∆ncal-∆nset)/∆nset,δT=(∆Tcal-∆Tset)/∆Tset.表3 表明,矩阵理论预测的结果相对于设定值的误差较小,δn和δT均不超过±5%.

4 结论

本文提出了由不对称半圆柱对阵列组成的全介质超构表面双参数传感器,通过分别引入三种不同形式的对称破缺,该超构表面均可以同时产生两个具有极高Q因子(导致透过率谱中极窄的线宽)和较高光谱对比度的QBIC 模式(记为QBIC1和QBIC2).QBIC1 和QBIC2 的Q因子与不对称参数均呈二次方反比关系,从而证实了这些模式均属于QBIC 模式,并且通过调节不对称参数,能够任意调节这些QBIC 模式的Q因子.对于不同形式的对称破缺,QBIC1 和QBIC2 的共振波长可能位于通常的谐振模式(记为Mx和My)的共振波长的同一侧或两侧;QBIC1 和QBIC2 的Q因子既有可能接近,也有可能差异较大;并且对于不同形式的对称破缺,产生QBIC 对入射光偏振方向的要求可能不同.

采用该对称破缺超构表面,通过测量透过率谱中两个QBIC 的谐振波长,能够实现折射率和温度的双参数传感,从而有效解决了环境中折射率和温度传感的串扰问题.对于折射率传感,QBIC1 模式的灵敏度达到194.7 nm/RIU,最大FOM 达到8197 (对应Q因子45829);QBIC2 模式的灵敏度达到170 nm/RIU,最大FOM 达到4970 (对应Q因子28097).对于温度传感,QBIC1 模式的灵敏度达到7.77 pm/℃,QBIC2 模式的灵敏度达到24 pm/℃.如果设置不对称参数进一步接近零,则可以进一步提高Q因子,从而进一步提升传感性能.此外,如果结构中同时引入多种对称破缺形式(即不对称参数α,β,γ中有两个或三个均不为0),则有可能对QBIC 模式实现更大自由度的调节,从而获得更丰富和优异的传感性能.