点间隧穿耦合对四能级三量子点电磁感应透明介质孤子动力学的影响*

王胤 王壬颍 陈桥 邓永和

1) (湖南工程学院计算科学与电子学院,湘潭 411104)

2) (湘潭大学物理与光电工程学院,湘潭 411105)

3) (湖南交通工程学院公共基础课部,衡阳 421001)

利用概率幅变分近似结合多重尺度法,研究了探测光在两边产生点间隧道耦合的非对称阵列型三量子点电磁诱导透明介质的传播性质.结果表明,由于系统的色散效应和点间隧穿耦合产生的非线性效应相平衡,系统能形成稳定传播的超低速时间光孤子.有趣的是,仅开启一边的点间隧穿耦合(即另一边关闭),随着点间隧穿耦合强度的增加,光孤子的速度呈现出先增大后减小的变化趋势,但光孤子的幅度却一直增大.两边两个点间隧穿耦合强度均开启后,随着点间隧穿强度逐渐的增大,光孤子的幅度随着点间隧穿强度的增大会出现逐渐减小,直到出现一个拐点后才迅速增大;而光孤子的速度相比较于单个隧穿强度的影响会明显降低,且出现停滞的现象.这些结果不但揭示出点间隧道耦合对三量子点电磁感应透明介质光孤子的动力学有着重要影响,而且还预言在半导体量子点器件中可利用点间隧道耦合调节其光孤子传输的幅度.

1 引言

光孤子是体系的色散(或衍射)效应与非线性效应相互作用平衡后的产物[1–9],在量子通信和量子信息处理过程中作为信息的载体不仅能承载巨大的信息量而且还可提高在长距离传输过程的信息保真度和稳定性[10–13].光孤子作为量子信息传输和处理过程中的载体的最早研究主要是超冷原子电磁感应透明(electromagnetic induction transparency,EIT)介质,这主要是因为该介质能通过弱光耦合到原子能级间产生量子相干和量子干涉效应激发出强的非线性效应[14–18].吴颖[19]发现在四能级超冷EIT 体系可通过强控制光去控制弱探测光形成超慢光孤子.随后研究表明,弱探测光在超冷EIT 体系所形成的超慢光孤子能稳定传播[20,21].本研究组[22]也发现四能级三脚架式超冷原子EIT 系统通过两个强控制光场既可控制体系光孤子的群速度匹配而且还调节亮孤子和暗孤子的转换.黄国翔等[23–28]证实通过控制光的开关效应可对光孤子进行存储和读取.然而,由于超冷原子EIT 介质只能在低温、稀薄的情况下才能实现,因而难以在大规模化器件中进行实施,付之于具体应用有一定的局限性.

随着半导体工艺的发展,半导体量子点不仅具有类似于超冷原子的分立能级,且其能级结构还可以通过“人工剪裁”方式去实现[29].当光束通过量子点内部,由于量子相干和量子干涉效应所引起的EIT 效应能通过弱光激发强的非线性效应,这为光孤子的形成及光信息的传输提供很好的应用前景[30–32].研究表明让一束探测光通过10 层量子点光学薄膜后,再通过控制光的调制可在体系观察到EIT 效应[33].当光通过半导体量子点EIT 介质后,由于系统的色散效应与强非线性效应相平衡,形成超低速时间光孤子[34–37].光孤子在半导体量子点EIT 介质中传播性质的研究有望为量子光信息的传输提供更加广泛的应用前景.

对于量子点EIT 体系,不但具备类似原子的分立能级,而且还可通过排列、堆叠等耦合方式形成量子点分子.在双量子点分子体系中,由量子点间隧穿耦合作用引起的量子相消干涉导致的透明窗口可以让光无吸收通过,称之为量子点间隧穿诱导透明(tunneling induces transparency,TIT)[38–42].Michael 等[43]发现点间TIT 不仅可以抑制介质对光的吸收,而且还可以调节光通过系统的传播速度.让一束探测光通过量子点EIT 介质去传播[44,45],发现体系所形成的光孤子能够存储起来.佘彦超等[46]发现通过调节TIT 强度能使体系产生双透明窗口,且系统所产生的时间孤子是亮孤子还是暗孤子完全由控制光强的强度来确定.目前实验上已通过分子束外延生长技术或原位原子层精确刻蚀技术制造出三量子点分子[47–50].相比于双量子点分子,三量子点分子具备两个量子点间隧穿耦合效应和更灵活可控的能级结构.Tian 等[51]发现可通过三量子点中的双隧穿实现双暗态共振从而增强体系的非线性效应.Luo 等[52,53]也证实三量子点分子中由于两个点间隧穿会使系统的克尔非线性显著提高,甚至还会导致系统出现自聚焦和自散焦效应.这意味着三量子点分子体系具有一系列新颖的非线性特性.然而,迄今为止对三量子点分子EIT介质的非线性动力学性质尤其是其中的光孤子动力学行为的报道尚少.

受此启发,本文基于现有实验条件,构建了由一束探测光耦合到中间量子点上,且两边两量子点产生点间隧道耦合而成为非对称的阵列型三量子点EIT 介质模型.随后利用概率幅变分近似结合多重尺度法,解析地研究了点间隧穿耦合对三量子点EIT 介质中的线性和非线性性质的调控效应;发现双点间隧穿耦合效应比单点间隧穿耦合对量子点EIT 介质的线性和非线性性质的调控能力更强.尤其是时间光孤子的振幅、速度均可通过量子点的点间隧穿耦合强度来调节;因而揭示出在半导体量子点器件中可利用点间隧穿耦合强度去调节其传输的光孤子的幅度.

2 模型和Maxwell-Schrődinger 方程

基于目前实验上制造三量子点分子技术[47–50],自组装GaAs 三量子点分子的能级结构示意图如图1 所示.它由三个不同尺寸的量子点排成一排,类似于两个不同大小的双量子点分子耦合、沿着生长方向应用于合适的门电压演练而成.由于量子点之间存在一定的势垒宽度阻碍了量子点中空穴的隧穿,因而仅考虑中间量子点上的电子与左(右)量子点之间的电子隧穿.实验上,以GaAs 为衬底,通过自组织生长与光刻蚀技术相结合,实现沿[110]方向并列生长的不均匀三重量子点.图1中 |0〉为基态,|1〉为一束频率为ω10的弱探测光将中间的量子点上的电子从价带激发到导带形成的直接激子态,|2〉或|3〉 表示量子点在外加门电压的作用后,左或右量子点的导带能级与中间量子点产生共振,从而中间的量子点内的电子分别隧穿到左或右两边量子点后所形成的间接激子态.因此,弱探测光和三个不同尺寸的量子点组合成四能级非对称阵列型三量子点EIT 介质模型.设图1 中的中间量子点与左、右两边量子点的点间隧穿强度分别为Te1和Te2.根据旋波近似和电偶极近似[10–13,41,42],四能级非对称阵列型三量子点EIT 体系在相互作用绘景中的哈密顿量为

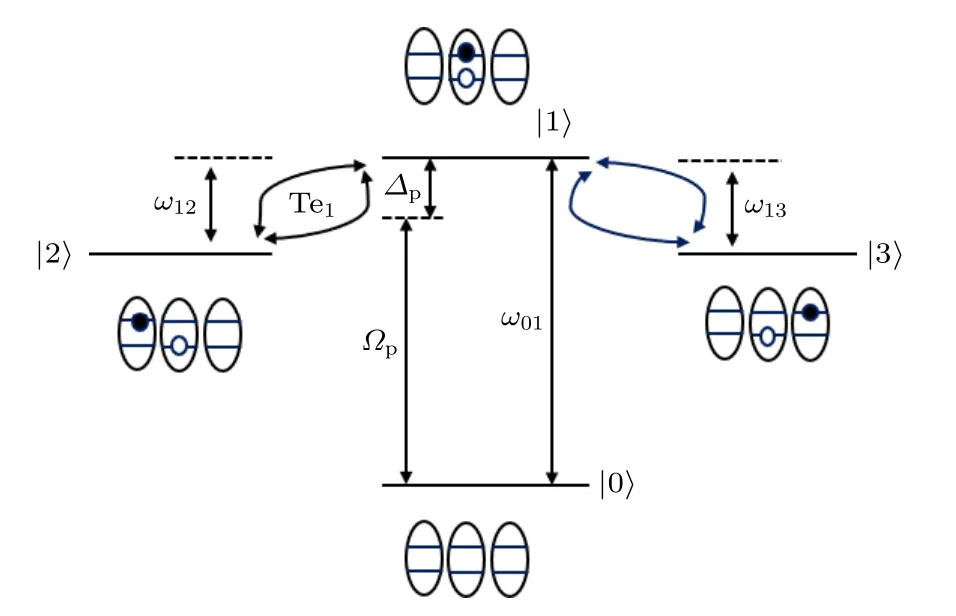
图1 四能级非对称阵列型三量子点电磁感应透明介质能级结构示意图Fig.1.Energy level structure diagram of a four-level asymmetric array-type three quantum dots electromagnetically induced transparent medium.

其中,∆1=ω10-ωp,∆2(3)=∆1+ω12(3),ωij表示电子在能级 |i〉与|j〉 之间的跃迁频率;弱探测光的频率为ωp,其拉比频率是Ωp=Epµ01/(2ℏ),Ep为探测光振幅,µij表示能级 |i〉→|j〉 之间的跃迁偶极矩.探测光的Maxwell 方程为[41,42]

式中,ε0和c分别是真空中的介电常数和光速.探测光的电场矢量为

其中,kp为探测 光波矢,c.c.表示复共轭函数.探测光的电极化强度为

式中,Na表示原子数密度;Aj表示能级 |j〉 的原子布居概率幅,满足守恒关系,

其中,dj=∆j+iγj(j=1,2,3),γj表示能级|j〉上的衰减率,由能级寿命展宽γjl和失相展宽γjd两部分组成,即γj=γjl+γjd,其中γjl主要是由于低温下纵波光学声子发射产生,而γjd主要是由于电子与电子,电子与声子散射以及表面粗糙所引起,传播系数为

随后,只要求解MS 方程(3),就可以获得系统的线性和非线性光学性质.

3 线性光学性质

一般情况下,MS 方程(3)难以直接获得其解析解,在此使用多重尺度法[41,42]对其进行近似求解.设

并设展开项均是多重尺度变量tl=εlt,zl=εlz(l=0,1,2)的函数;ε是描述各态布居衰减相关的特征小量.将多重尺度各参量代入方程(3),可得

式中,右边各表达式分别为

当j=1时,设Ωp(1)=εF1exp[i(K(ω)z0-ωt0)],代入(4)式可得探测光的线性色散关系为

方程(5)在ω=0 处进行泰勒展开:

由于Kj是一个复数,它可以写成Kj=Kjr+iKji,这里K0r,K1r和K2r分别代表K0,K1和K2的实部;K0i,K1i和K2i分别代表K0,K1和K2的虚部.进而可以得到:

在(6a)式中,Vg表示探测光在系统中传播的群速度,(6b)式则表示系统的群速度色散效应.

为获取系统中探测光的K0i线性吸收特征,将探讨量子点间隧穿耦合对体系探测光场的线性吸收特性的影响,随后绘制出不同的量子点间隧穿耦合(实验可通过门电压控制)情况下系统吸收参量K0i随探测光失谐量∆p的变化情况.图2 展示了关闭图1 中的左边点间隧穿耦合,仅开启右边一个点间隧穿耦合情况下系统的线性吸收性质.当两个点间隧穿耦合均关闭时,即Te1=Te2=0 (图2中黑点线),可以看出当门电压断开时,探测光在失谐量(∆p=0) 区域被大大地吸收.当Te1=0 和Te2=20 μeV (图2 红实线),即左边量子点间隧穿耦合仍然处于关闭状态仅开启右边一个点间隧穿耦合情况下,系统中出现一个透明窗口.也就是说,只有开启点间隧穿耦合,体系才有可能产生透明窗口.这类透明窗口是由于量子点间隧穿所引起,又称为TIT 窗口.这是因为开启右边的点间隧穿耦合后,Te2使跃迁通道 |0〉→|1〉和|1〉→|3〉 之间发生干涉相消,使得能级 |1〉和|3〉 的布居进入暗态,从而探测光在TIT 窗口内几乎不被吸收.当右边的点间隧穿耦合Te2进一步增强时,即Te1=0 和Te2=40 μeV (图2 蓝虚线),与红实线相比,量子点间TIT 窗口的宽度变宽.

图2 关闭左点间隧穿耦合 (Te1=0) 仅开启右点间隧穿耦合情况下,线性吸收系数 K0i 随失谐 ∆p 的变化情况.其他参数: γ10=3.3 μeV ,γ20=γ30=10-4γ10 ,-ℏω12=ℏω13=10 μeV,κ01=1976 cm-1·μeVFig.2.In the case that the left (right) inter-dot tunneling coupling is turned off (on),the linear absorption coefficient K0i as a function of the detuning ∆p .Other parameters:γ10=3.3 μeV ,γ20=γ30=10-4γ10 ,-ℏω12=ℏω13=10 μeV,and κ01=1976 cm-1·μeV .

为了获得左、右点间隧穿耦合效应对非对称阵列型三量子点EIT 体系探测光线性吸收的不同特征,图3 绘制出关闭右边量子点间隧穿耦合仅开启左边一个点间隧穿耦合情况下系统的线性吸收性质.通过与图2 比较,可以发现与图2 唯一不同的曲线特征是: 开启右边点间隧穿耦合的图2 的TIT窗口的中心位置原偏离在∆p=0 的左边,而开启左边的点间隧穿耦合后TIT 窗口的中心位置偏离在∆p=0 的右边;其他结果如透明窗口的宽度随着点间隧穿耦合强度的增大而变宽类似于图2.因此在下面讨论单个点间隧穿耦合对非对称阵列型三量子点EIT 体系物理性质的影响时,只需考虑其中一种情况.

图3 关闭右点间隧穿耦合 (Te2=0) 仅开启左点间隧穿耦合情况下,线性吸收系数 K0i 随失谐 ∆p 的变化情况.图中所使用的其他参数与图2 一致Fig.3.In the case that the left (right) inter-dot tunneling coupling is turned on (off),the linear absorption coefficient K0i as a function of the detuning ∆p .Other parameters used are the same as the Fig.2.

既然仅开启左边或右边的一个点间隧穿耦合,三量子点EIT 体系均会出现一个TIT 窗口.当左右两边两个点间隧穿耦合均开启后,三量子点EIT 体系的线性吸收性质如图4 所示.当Te1=Te2=20 μeV (图4 红实线),此时三量子点EIT体系呈现出两个TIT 窗口,这与双量子点分子中的单量子点间TIT 窗口完全不同.双TIT 窗口是由两个点间隧穿耦合效应的量子相消干涉效应所引起,这与超冷原子系统中由控制场引起的量子相消干涉效应所导致的EIT 窗口完全不同.当两个隧穿耦合增强时,即Te1=Te2=40 μeV (图4 蓝虚线),双TIT 窗口的宽度比红实线的双TIT 窗口的宽度更宽.从此可得,随着单量子点和/或双量子点间隧穿耦合强度的增大,三量子点体系的单和/或双TIT 窗口的宽度都变宽.

图4 左、右两边两个点间隧穿耦合均开启情况下,线性吸收系数 K0i 随失谐 ∆p 的变化情况.图中所使用的其他参数与图2 一致Fig.4.Under both the left and right inter-dot tunneling coupling are turned on,the linear absorption coefficient K0i as a function of the detuning ∆p .Other parameters used are the same as the Fig.2.

4 非线性光学性质

在此探讨非对称阵列型三量子点EIT 体系的非线性光学性质,即MS 方程在多重尺度近似展开后的二阶和三阶情况.当j=2 时从方程(4)整理化简消除久期项有

同理,当j=3时,类似地消除久期项,整理可得

其中,体系的非线性效应表示为

该式描述了包络函数F1在介质中的演化方式,方程(8)为复系数的非线性薛定谔方程,将其返回到原变换关系zl=εlz,tl=εlt,U=εF1e-ImK,并引入新参数ξ=z/LD,和τ=t-z/Vg,整理可得

根据现有实验室制造三量子点条件,选择非对称阵列型三量子点EIT 体系的参数[45–48](除特殊说明,图5—图8 均采用此参数):γ1=0.054 meV,γ2=γ3=5.4×10-5meV;探测光的传播系数κ01=340 meV·μm-1;失谐量∆1=0.1674 meV,∆2=0.6480 meV,∆3=0.6840 meV,τ0=3×10-8s .在此,先分析单个点间隧穿耦合情况下三量子点EIT 体系所形成的孤子.作为一个典型的示例,设Te1=1 meV且Te2=0,即开启左边两量子点的点间隧穿耦合,关闭右边点间隧穿耦合情况下,可计算出参数:

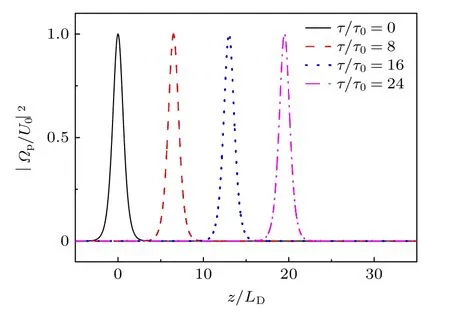
图5 单点间隧穿耦合下三量子点EIT 介质中光孤子的稳定性分析(Te1=1 meV,Te2=0)Fig.5.Stability analysis of optical solitons in the three quantum dot EIT medium under the single inter-dot tunneling coupling effect (Te1=1 meV,Te2=0).

为了检验亮孤子在三量子点EIT 介质中传播的稳定性,对光孤子的波形 |Ωp/U0|2增加5%的微扰后探究其随时间的演化情况,如图5 所示.可以看出,在初 始时刻探测光 |Ωp/U0|2在z/LD=0 位置形成一亮光孤子.随着时间的推移如t=8τ0,可以看到该亮孤子能保持波形的幅度和宽度不变,且稳定地向右传播;当时间进一步推移至t=16τ0和t=24τ0时,孤子的幅度和宽度仍能保持不变地向右传播.这说明单个点间隧穿耦合情况下的三量子点EIT 介质中能产生光孤子,并可稳定地传播.

既然单个点间隧穿耦合情况下体系的光孤子能够稳定地传播;接着探讨两边两个点间隧穿均开启后,系统光孤子的稳定性.作为一个典型示例,选取Te1=1 meV 且Te3=0.5 meV时,可计算出参数:

图6 双点间隧穿耦合下三量子点EIT 介质中光孤子的稳定性分析(Te1=1 meV,Te2=0.5 meV)Fig.6.Stability analysis of optical solitons in three quantum dot EIT medium under the two single inter-dot tunneling coupling effect (Te1=1 meV,Te2=0.5 meV).

通过对比图5 和图6 就会发现,在相同的时间间隔内光孤子的传播距离相差很大.这说明在非对称三量子点EIT 介质中,当系统左右两个点间隧穿均开启后由于左右两边这两个点间隧穿的共同作用,使光孤子的速度大幅度地降低;这对探测光所形成的光孤子动力学影响非常大.从而,图7 给出了在不同的右点间隧穿强度Te2下,孤子的群速度Vg随左点间隧穿强度Te1的变化情况.从图7(a)中可以看出,当Te2=0 时即关闭图1 右边的点间隧穿耦合仅开启左边的点间隧穿耦合情况下,三量子点EIT 介质中孤子的群速度Vg随着单点间隧穿耦合强度的增大呈现出先逐渐增加随后减小的变化趋势.当图1 中的左右两边两个点间隧穿都开启后,从图7(b)中可以看出,当Te2=0.5 meV 时(黑实线),随着 Te1的增大,孤子的群速度Vg逐渐减小;进一步增加图1 右边的点间隧穿耦合强度,当Te2=1 meV时(蓝虚线),相比图7(a)中孤子群速度降低了2 个数量级,且随着Te1的增大逐渐减小.这说明在左右两边两个量子点间隧穿耦合效应的共同作用下,三量子点EIT 介质中的光孤子传播速度会被抑制,以致于当左右两边两个量子点间隧穿耦合都较大时,三量子点EIT 介质中的孤子会出现停滞现象.

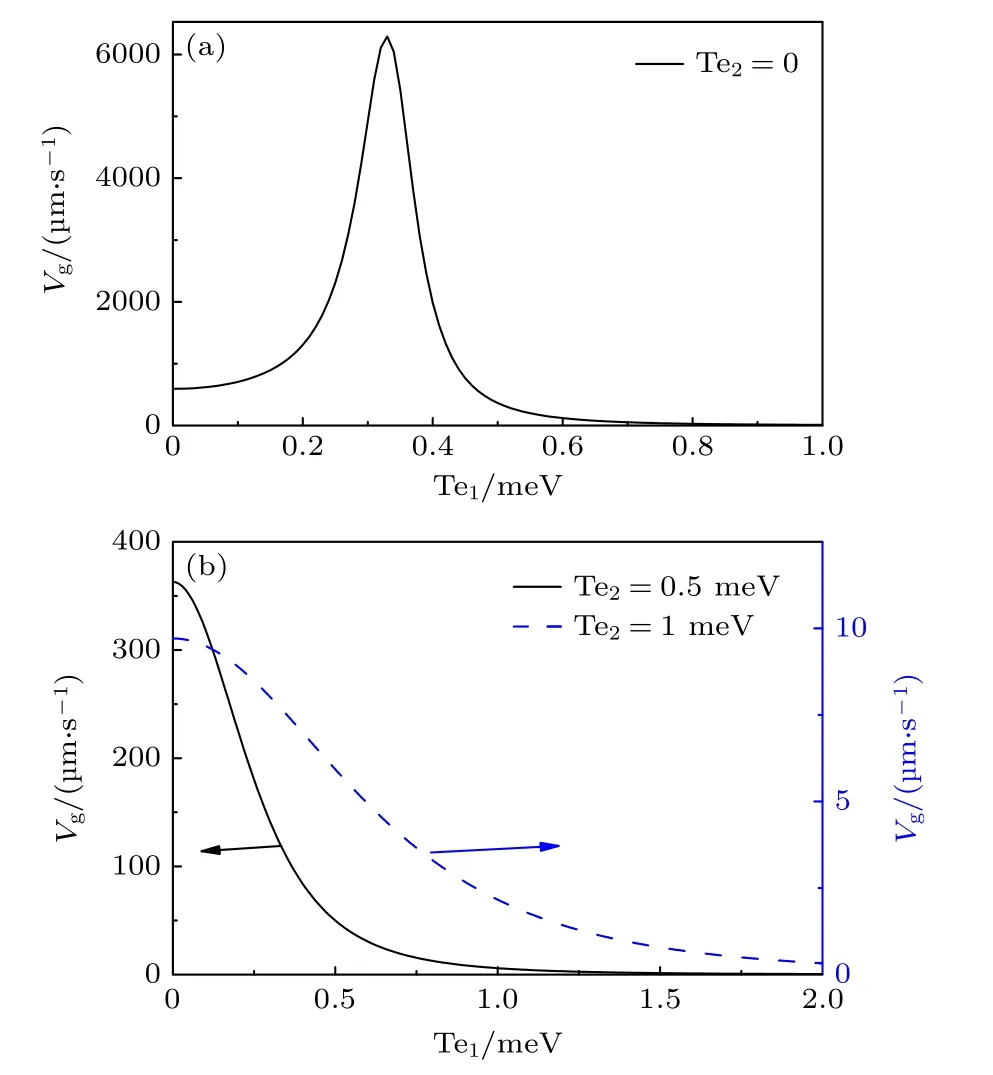
图7 不同右点间隧穿强度下孤子的群速度随左点间隧穿强度Te1 的变化Fig.7.Group velocity of the solitons as a function of the strength Te1 of the left inter-dot coupling with the different strength of the right inter-dot tunneling coupling.

最后,探讨点间隧穿耦合强度对三量子点EIT介质中孤子幅度的影响,如图8 所示.当Te2=0时(如图中粉红色实线),即关闭三量子点EIT 介质右边的点间隧穿耦合仅开启左边的点间隧穿耦合情况下,三量子点EIT 介质中孤子的幅度随着单点间隧穿耦合强度的增大而逐渐增加.开启三量子点EIT 介质右边的点间耦合效应且其强度比较小(如Te2=0.5 meV)时(见图中蓝点划线),也就是当三量子点EIT 介质中的左右两边两个点间隧穿都开启后,发现三量子点EIT 介质中孤子的幅度随着左点间隧穿耦合强度的增加反而减小.进一步增加右边的点间耦合强度Te2=1.0 meV,发现三量子点EIT 介质中孤子的幅度随着左点间隧穿的增加呈现出先减少而后增加的变化趋势;当右边的点间耦合强度进一步增加到Te2=1.5 meV时,三量子点EIT 介质中孤子的幅度还是随着左点间隧穿的增加出现先减少而后增加的变化趋势,且极小值拐点沿左点间隧穿耦合强度较小的值移动.

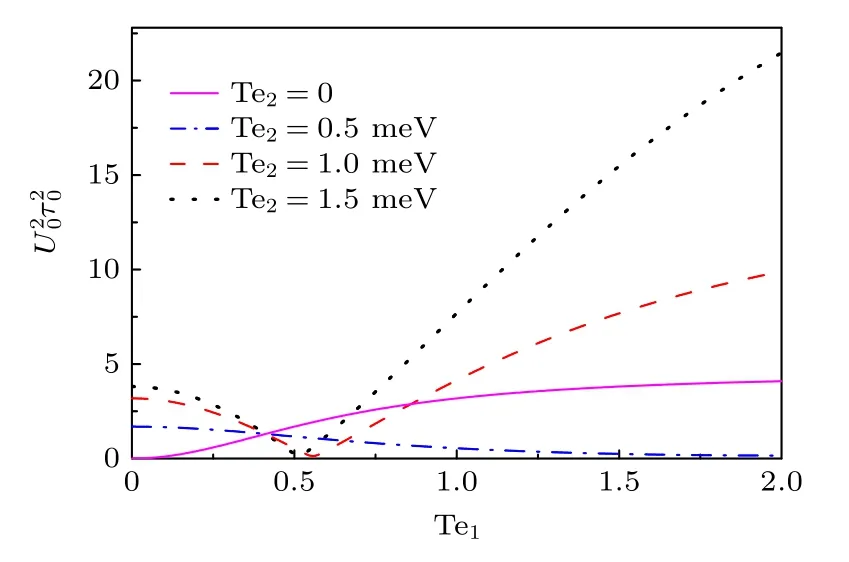
图8 不同右点间隧穿强度下,孤子的幅度随左点间隧穿强度Te1 的变化Fig.8.Amplitude of the solitons as a function of the strength Te1 of the left inter-dot coupling with the different strength of the right inter-dot tunneling coupling.

5 结论

基于目前实验制造量子点分子技术,先构建了两边产生点间隧道耦合的非对称阵列型三量子点EIT 介质模型.随后利用概率幅变分近似结合多重尺度法,解析地研究了点间隧穿强度对体系线性和非线性性质的影响.结果发现只有开启点间隧穿耦合,体系才会产生TIT 透明窗口.仅开启一个点间隧穿耦合(即另一个关闭),三量子点EIT 介质中仅出现单个TIT 窗口,且透明窗口的宽度随着点间隧穿强度的增加而变宽.关闭右边点间隧穿耦合开启左边一个点间隧穿耦合与关闭左边点间隧穿耦合开启右边一个点间隧穿耦合,TIT 窗口唯一的不同是: 透明窗口的中心位置由偏离在∆p=0 的右边演化为偏离在∆p=0 的左边.当两边两个点间隧穿耦合均开启时,三量子点EIT 体系呈现出两个TIT 窗口,当体系的两个隧穿耦合增强时,双TIT 窗口的宽度变宽.

当体系的线性色散效应和量子点间隧穿耦合所产生的非线性效应相互作用达到平衡后能形成超低速时间光孤子,且可稳定地传播.有趣的是,当仅开启一边的点间隧穿耦合(即另一边关闭),随着点间隧穿耦合强度的增加,光孤子的速度呈现出先增大后减小,而光孤子的幅度则一直增大.当两边两个点间隧穿耦合强度均开启后,随着点间隧穿强度逐渐的增大,光孤子的幅度随着点间隧穿强度的增大会呈现出逐渐减小,直到出现一个拐点后才迅速增大;而光孤子的速度相比较于单个隧穿强度的影响会明显的降低,且出现停滞的现象.相对于只有一个隧穿的双量子点,具有双隧穿的三量子点孤子的传播行为都具有更强的调控能力.这说明点间隧道耦合对三量子点体系的光孤子动力学有着重要影响,因而可利用点间隧道耦合对半导体量子点器件中的光孤子进行调幅操作,这些结果为量子点器件实现光孤子通信提供了一定的理论依据.