Gyro-Landau-fluid simulations of impurity effects on ion temperature gradient driven turbulence transport

Yifei LIU (刘逸飞) and Jiquan LI (李继全)

Southwestern Institute of Physics,Chengdu 610041,People’s Republic of China

Abstract The effects of impurities on ion temperature gradient (ITG) driven turbulence transport in tokamak core plasmas are investigated numerically via global simulations of microturbulence with carbon impurities and adiabatic electrons.The simulations use an extended fluid code (ExFC)based on a four-field gyro-Landau-fluid (GLF) model.The multispecies form of the normalized GLF equations is presented,which guarantees the self-consistent evolution of both bulk ions and impurities.With parametric profiles of the cyclone base case,well-benchmarked ExFC is employed to perform simulations focusing on different impurity density profiles.For a fixed temperature profile,it is found that the turbulent heat diffusivity of bulk ions in a quasi-steady state is usually lower than that without impurities,which is contrary to the linear and quasilinear predictions.The evolutions of the temperature gradient and heat diffusivity exhibit a fast relaxation process,indicating that the destabilization of the outwardly peaked impurity profile is a transient state response.Furthermore,the impurity effects from different profiles can obviously influence the nonlinear critical temperature gradient,which is likely to be dominated by linear effects.These results suggest that the improvement in plasma confinement could be attributed to the impurities,most likely through adjusting both heat diffusivity and the critical temperature gradient.

Keywords: gyro-Landau-fluid simulation,impurity effects,ion temperature gradient mode,turbulence transport

1.Introduction

In toroidal magnetically confined fusion devices such as tokamaks,the levels of particle and energy transport are generally observed to be far above those derived through theoretical predictions based on collisional relaxation processes.This phenomenon is called ‘anomalous transport’and it severely degrades the confinement performance of devices [1].Microturbulence caused by drift wave instabilities,e.g.,the ion temperature gradient (ITG) mode,is one of the leading candidates for explaining the transport [2-5].Suppressing turbulence and controlling transport are important for achievement of high-performance plasmas and realizing fusion energy.

Impurity ions unavoidably exist in tokamaks due to the interaction of plasmas with the first wall and divertor and even small amounts affect the confinement level of plasmas[6,7].External impurity injection has been observed to lead to ion heat diffusivity (χi,heat flux divided by the temperature gradient) reduction and confinement improvement in various experiments [8-10].Therefore,impurity injection is a promising way to control turbulence transport and the effects of impurities on microturbulence deserve in-depth study.Some theoretic analyses and numerical simulations found that low-or medium-Z impurities can destabilize or stabilize micro-instabilities under certain conditions.For example,an impurity mode may be excited when the impurity density is outwardly peaked,even if the temperature profiles of bulk ions and impurities are flat.Linear analysis found that the impurity mode can strongly couple with the ITG mode and enhance the growth rate of micro-instability[11-13].In addition,it was derived theoretically that impurity effects weakly influence the residual level of long wavelength zonal flow [14],which can regulate turbulence and affect the transport.Nonlinear simulations demonstrated the density profile evolution caused by particle transport induced by impurities [15].In short,impurities affect microturbulence and transport in many ways and therefore a comprehensive and reliable transport model is required to investigate their effects.

First-principles gyrokinetic codes can simulate turbulence with impurities accurately,but the simulations are expensive in terms of computing time.While some studies have been conducted,they are limited to a very small number of simulation cases.A fluid model may provide a more efficient and faster approach,enabling significant savings in terms of computing time and cost compared to gyrokinetic simulations.However,it lacks some important kinetic effects,e.g.,the so-called Landau damping and the finite Larmor radius (FLR),when the gyroradius of the impurity greatly differs from that of the bulk ions.The gyro-Landau-fluid (GLF) model [16-18],which involves the important kinetic effects above and a set of improved fluid equations,could exploit the merits of both gyrokinetic and fluid models and possibly provide a flexible alternative.We use the GLF model to simulate collisionless electrostatic ITG turbulence with impurities and adiabatic electrons.

In this work,a well-benchmarked GLF model with impurity dynamics is advanced based on the reduced four-field GLF model [18].A number of simulations with parametric profiles of the cyclone base case (CBC) [19] and different initial carbon impurity profiles in core plasmas are performed using the extended fluid code (ExFC) to investigate the impurity effects from two perspectives.First,considering that the heat flux mainly results from bulk ions on account of the small impurity fraction,we focus on the impurity effects on χiin ITG turbulence.For a fixed temperature profile,the results indicate that χibarely exceeds the level found in the case without impurity in the quasi-steady state -even with an initial impurity profile that destabilizes the ITG mode.This may be ascribed to the steep density gradients of both the ions and the impurities being relaxed quickly (within the magnitude of 1 ms) to a flatter one by particle transport induced by impurities.Fast relaxation indicates that the destabilization of the outwardly peaked impurity profile is a transient state response.Second,note that the ITG turbulence could be regulated by zonal flow and quenched in a low temperature gradient and that an upshift from a linear critical temperature gradient in a nonlinear simulation has been observed,i.e.the so-called Dimits shift.In fact,the impurity effects on nonlinear critical temperature gradient are also of interest.Simulations show that the critical temperature gradient can be influenced obviously by impurities with different profiles,e.g.,the nonlinear critical temperature gradient can be decreased by an outwardly peaked impurity.With further investigation,it appears that the impact of impurities on the nonlinear temperature gradient is likely dominated by linear effects.In addition,due to the change of the dominant driving source from the temperature gradient to the impurity density gradient,the heat diffusivity of turbulence at a linear critical temperature gradient is only at the neoclassical transport level.

The remainder of this paper is organized as follows.The physical model and numerical setting for the equilibrium profiles in the simulations are detailed in section 2.Section 3 exhibits linear and nonlinear benchmarks of ExFC with other codes.In section 4,simulation results with different impurity profiles are presented,focusing on the impurity effects on the ITG turbulence transport and the critical temperature gradient of turbulence.Finally,a summary of the main results and a brief discussion are given in section 5.

2.Physical model and numerical setting

ExFC is a global fluid-type turbulence and transport code,which applies a three-dimensional (3D) finite difference method to solve fluid equations [20,21].The solution of the Poisson equation and the evaluation of Landau damping and FLR terms are calculated by employing the spectral method.Under the fluid solver framework of ExFC,various fluid modeling equations can be solved conveniently with low CPU cost.To simulate low-or medium-Z impurity effects on electrostatic ITG turbulence properly and self-consistently,the collisionless four-field GLF model,namely,the GLF 3+1 model with adiabatic electrons,is applied in ExFC.The equations of bulk ions and impurities used in ExFC are different slightly from those in [18] as follows:

where nj1,uj‖,Tj1‖and Tj1⊥are,respectively,normalized perturbative gyro-center density,parallel velocity,and parallel and perpendicular temperature.nj0and Tj0are normalized equilibrium density and temperature,index j=i,z stands for the particle species (bulk ion or impurity),and Zjand Ajare the normalized charge number and mass number.B=B0R0/ (R0+r cos θ),and R0 are the minor and major radii,aspect ratio ϵ0=a0/R0,ρs0=mHcs0/eB is the hydrogen ion sound gyroradius and cs0=(Tref/mH)1/2is the hydrogen ion sound speed,and nrefand Trefare electron equilibrium density and temperature in the reference position,which is typically chosen to be the center of the radial domain,i.e.,r=0.5a0.I0is a modified Bessel function,1,2,3,4,5)are the toroidal closure coefficients.The values of νsrand νsiare taken form [18].The toroidal closure terms are calculated in the local limit to speed up the simulations.To simulate Rosenbluth-Hinton residual flow accurately [22],all νsare set to zero for the n=0 mode (n stands for the toroidal mode number) and the operator ∇‖is modified according to [23].A nice verification with analytical solutions will be shown in section 3.Nonlinear terms Nn,Nu‖,NT‖,NT⊥contain the usual E × B nonlinearities and additional FLR nonlinearities,as follows:

where vΨ· ∇=b × ∇Ψ · ∇=(∂rΨ∂θ-∂θΨ∂r)/r.The Poisson equation is written as

Here,an adiabatic electron response is assumed,then ne=ne0(ϕ -〈ϕ〉)/Te0,where 〈ϕ〉 represents the magnetic surface average of the electrostatic potential.In addition,the normalization is of the gyroBohm type;namely,the time and spatial coordinates are normalized by a0/cs0and ρs0:

The nonlinear equations (1)-(4) and Poisson equation (9)are numerically solved in usual circular geometry coordinate (r,θ,φ).The evaluation of FLR and Landau damping terms and the solution of the Poisson equation are calculated in spectral space (r,m,n),and the Padé approximation is employed to calculate Γ0in ExFC.In this work,simulations are carried out with parametric profiles of the CBC,including the equilibrium bulk ion and impurity density profiles:

the equilibrium temperature profiles:

and the safety factor profile:

Here,fz=Zznz0/nrefrepresents the impurity fraction at r=0.5a0which is the reference surface in the CBC profile.We set ϵ0=0.36,a0=150ρs0,R0/Lni=2.22,Lnz,LTjand fzas the parameters investigated in this work,and the range of the radial domain in the simulation is set from 0.1a0to 1.0a0to avoid singularity.The GLF 3+1 model is suitable for simulating the ITG turbulence with light impurities,so we simulated hydrogen bulk ions hybrid with carbon impurities C6+,which means Ai=1,Zi=1,Az=12 and Zz=6.We assume that the impurities are completely thermalized by ions,i.e.,Te0(r)=Ti0(r)=Tz0(r),and that the equilibrium temperature gradient is fixed in this work,which means that a self-consistent thermal source is included in the model to avoid temperature profile relaxation in the simulations.

3.Linear and nonlinear benchmark of ExFC

The GLF 3+1 model used in ExFC in this work has been well benchmarked in linear and nonlinear ITG cases without impurities.Here,linear verification is displayed through comparing the ExFC simulation results with those from gyrokinetic theories and codes,including linear growth rate and frequency of electrostatic ITG and residual flow level in CBC profiles,where R0/LT=6.92,growth rate and frequency versus kθρs0compared with GTC and FULL cases[24] are shown in figure 1.There is good agreement among the three codes.Residual flow level versus r and kris shown in figure 2,where the red line represents the analytical solution from [25].The divergence in the high krregion in figure 2(b) may result from a lack of trapped particles in the GLF 3+1 model.Considering that the zonal flow is mainly distributed in the low krregion,the divergence is acceptable.

In nonlinear cases,we scan heat diffusivity χiversus R0/LTand compare the results with those from the Lawrence Livermore National Laboratory (LLNL) fitting curve [19]and GYRO [26].χiis calculated by measuring the timeaveraged heat flux near r=0.5a0.The scan agrees well with others,as shown in figure 3,but the critical gradient is a little lower than those values (about 6.0) from the LLNL fitting curve and GYRO code.

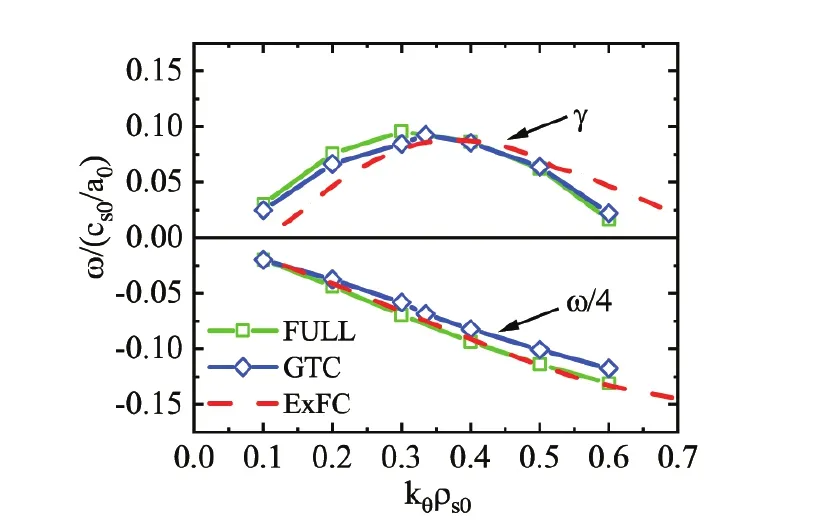
Figure 1.Comparison of growth rate γ and frequency ω scaled down by a factor of 4 for varying kθρs0 ∝ n in the CBC profile.The FULL and GTC data are from reference [24].

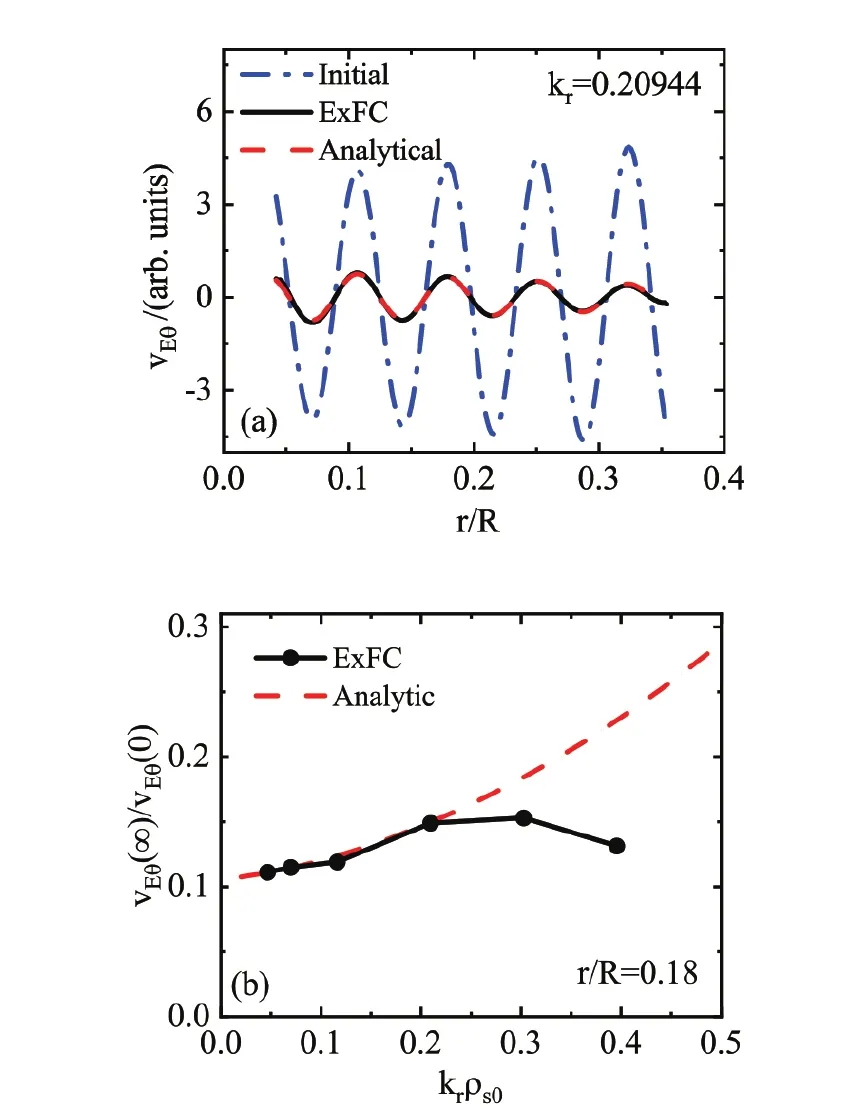
Figure 2.Comparisons of the residual level of zonal flow with the analytical solution.(a) Initial and residual flow at different radial positions with krρs0=0.20944,(b) residual level of zonal flow with different kr at r/R0=0.18.

4.Impurity effects on ITG turbulence

Based on the well-benchmarked model,we have performed linear and nonlinear global ITG simulations with C6+impurities in different initial profiles.Considering that the central accumulation of light impurities could not cause as strong radiation as heavy impurities,here we are more interested in the effects of impurity on the turbulence transport of bulk ions rather than the transport of impurities.There have been numerous linear eigenvalue calculations and quasi-linear estimations of the impurity effects on ITG instability and associated turbulent transport [13,20,27,28],but a nonlinear global simulation is necessary to predict the saturation level of turbulence and the profile evolution with impurities self-consistently.The parameters of the impurity profile are set conservatively according to impurity seeding experiments [8,9,29],e.g.,in nonlinear cases,fzranges from 0%to 18%,corresponding to an effective charge numberof about less than 2.7.We will show global simulations of the impurity effects on linear ITG instability in section 4.1,nonlinear heat diffusivity χiin section 4.2 and critical temperature gradient R0/LTcritin section 4.3.

4.1.Linear simulations

Figure 4 displays the growth rate of the global ITG mode calculated from linear simulations of ExFC for different fzand R0/Lnzwith R0/LT=6.92.In figure 4(a),results of varying fzat fixed R0/Lnz=-8.88 indicate that the destabilization of outwardly peaked impurities increases with fzuntil fz～ 21%;more impurities dilute bulk ions,so the growth rates decrease.Meanwhile,figure 4(b) demonstrates the ITG growth rate for different R0/Lnzat fixed fz=12%.Compared with the case without impurities,it is destabilized when R0/Lnz≲ -2.22 and stabilized when R0/Lnz≳ -2.22.It can be seen that the impurity effects behave as a competition between destabilization of the impurity density gradient and stabilization induced by the impurity dilution of bulk ions.The results of ExFC global simulations are consistent with those from gyrokinetic eigenvalue calculations [13,28].

Figure 3.Comparison of χi versus R0/LT scan with GYRO and the LLNL fitting curve in the CBC profile.The GYRO data is from reference [26] and the fitting curve is equation (1) in reference [19].

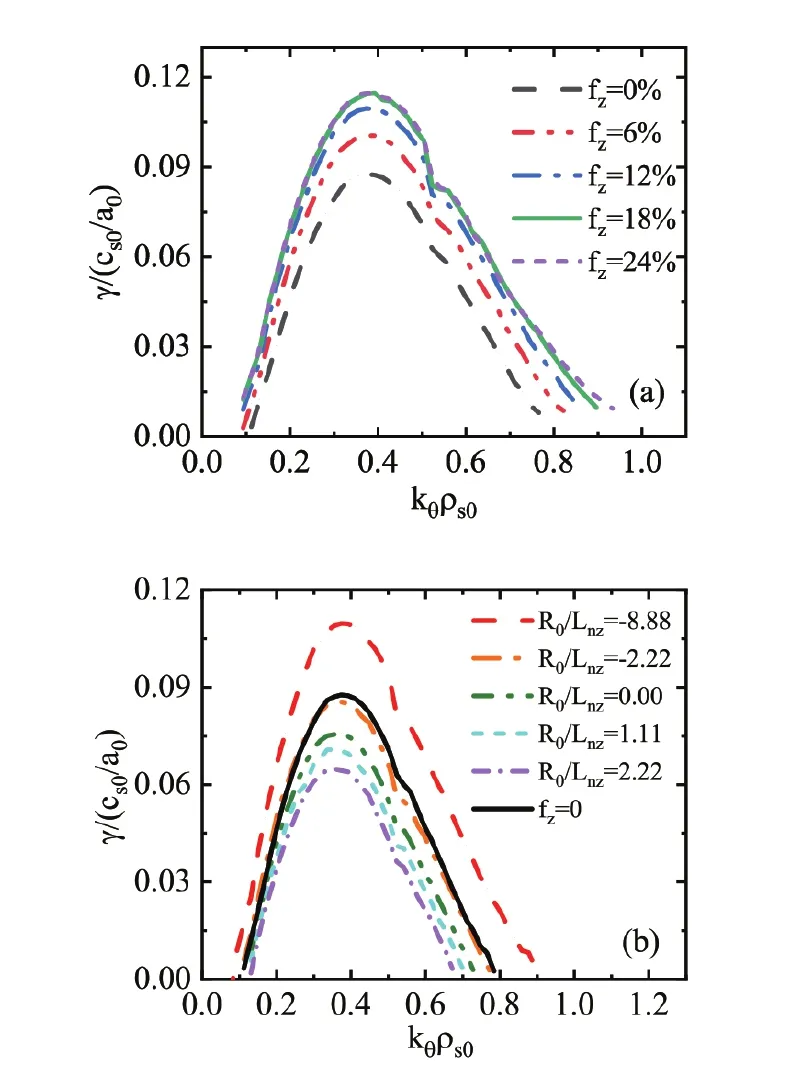
Figure 4.Scan of γ versus kθρs0 at fixed R0/LT=6.92 for different impurity fractions fz (a) and impurity density gradients R0/Lnz (b).

4.2.Heat diffusivity

In section 4.1,several linear simulations show the different impurity effects on ITG,which are determined by the impurity density profile.For the destabilization profile,i.e.,an outwardly peaked impurity density profile,quasi-linear analysis predicts a stronger heat flux than the case without impurities [30],but it is different from the nonlinear simulations of ExFC due to the fast relaxation of density profiles induced by impurity and ion transport.

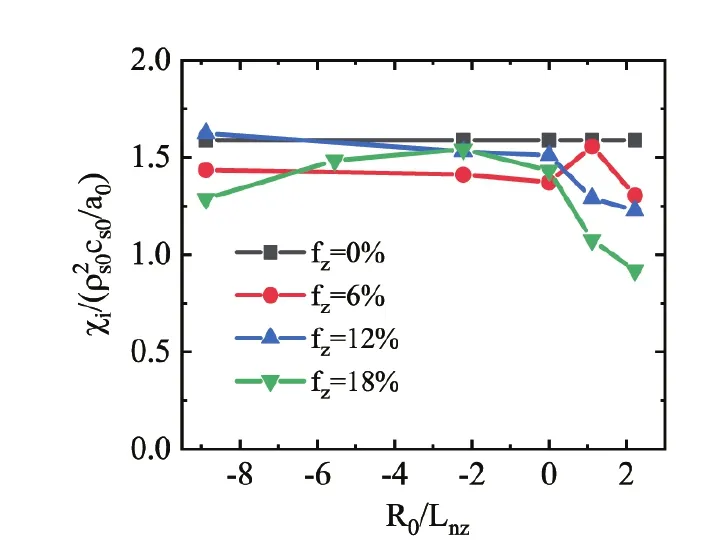
Figure 5.Averaged χi in the quasi-steady state with fixed R0/LT=6.92 for different impurity fractions fz and impurity density gradients R0/Lnz .

We have performed 16 simulations of the ITG turbulence transport for different fzand R0/Lnzwith R0/LT=6.92.The time-averaged heat diffusivity χiin the quasi-steady state (t ＞ 1000a0/cs0) near r=0.5a0is summarized in figure 5.Results show that the values of χiin most cases are lower than the level without impurities.To clarify the underlying mechanism,the evolutions of density gradients and χiof two typical cases with inwardly and outwardly peaked impurity density profiles are shown in figures 6 and 7.The density gradients are calculated by performing a time average on the sum of n0and 〈n1〉.The variations of R0/Lnand χiin the inward case are not obvious within 2000a0/cs0,while the outward case exhibits fast relaxation of R0/Lnand χi.Figure 8 demonstrates the degraded linear growth rate from an initial to quasi-steady state with outwardly peaked impurities,which makes the lower χiin figures 5 and 7(b) reasonable and the nonlinear results consistent with quasi-linear analyses.

With assumed reference parameters for normalization,namely Tref=1 keV and B=1 T,the relaxation processes in figure 5 are estimated within several milliseconds and the result is consistent with that from a impurity seeding experiment [29].Hence,the destabilization of the outwardly peaked impurity profile is a temporary process compared to the high confinement discharge time,i.e.,the impurity destabilization is a transient state response.However,the dilution of bulk ions by impurities is persistent,so the level of heat diffusivity can rarely exceed that without impurities in a quasi-steady state.With the assumption of a lack of recombination and radiation of impurities,plasma confinement can be probably improved.

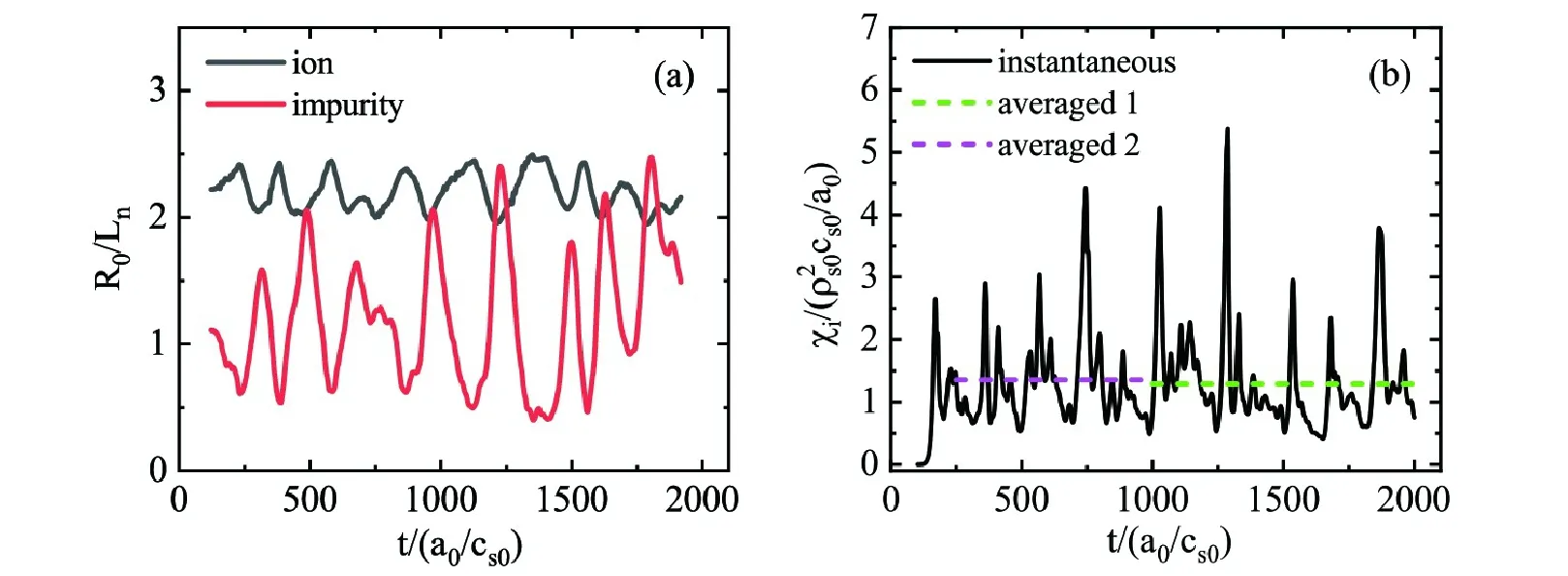
Figure 6.Time evolution of density gradient R0/Ln (a) and heat diffusivity of bulk ion χi (b) with initial profiles for R0/LT=6.92,fz=12% and R0/Lnz=1.11.The averaged diffusivity before and after t=1000a0/cs0 are plotted in (b) by dashed lines.

Figure 7.Same as in figure 6 except for R0/Lnz=-8.88.

Figure 8.Growth rate versus kθρs0 for an initial profile with R0/LT=6.92,R0/Lni=2.22,fz=12%,R0/Lnz=-8.88 (solid curve),and for a quasi-steady state profile with R0/LT=6.92,R0/Lni=1.3,fz=12%,R0/Lnz=-2.13 (dash dot curve).The case without impurities is also plotted by a dashed curve.

4.3.Critical temperature gradient

Considering that impurities can destabilize or stabilize the ITG mode,the critical gradient of instability or turbulence transport should theoretically be influenced by impurities.Moreover,in a nonlinear ITG simulation,zonal flows increase due to the accumulation of undamped residues that eventually quench the turbulence with a low temperature gradient,leading to a nonlinear upshift of the critical temperature gradient from a linear one [19].Therefore,the impurity effects on the critical temperature gradient are investigated via ExFC.

Several linear simulations with a zero growth rate or nonlinear simulations with quenched turbulence for different profile parameters (R0/LTcrit,fz,R0/Lnz) are shown in figure 9(a).The nonlinear cases with quenched ITG turbulence are distinguished via a shotting method that selects the quenched cases with different parameters (R0/LT,fz,R0/Lnz)within a time duration of 3000a0/cs0.The relations between fzand R0/LTcritat different R0/Lnzare expressed by several fitting lines in figure 9(a).The lines indicate that impurity effects can improve or reduce the plasma confinement performance by increasing or decreasing the critical temperature gradient.

Before discussing the impurity effects on the critical gradient,nonlinear simulations that remove zonal flow artificially are carried out with an impurity.However,no nonlinear upshift is found,which means that the impurity has no direct influence on the critical gradient.Denoting the nonlinear critical gradient as R0/LNLc,the linear critical gradient as R0/LLcand the upshift caused by zonal flow as SZF,we can write with confidence that:

Figure 9.(a) Fitting lines of linear (dashed line) and nonlinear (solid line) critical temperature gradient versus impurity fraction fz with different R0/Lnz,(b) heat diffusivity χi of turbulence without impurity and with impurity near the critical temperature gradient.Lines are labeled by the values of parameters (fz,R0/Lnz).

After excluding the direct influence of impurity effects on R0/LNLc,we label the strength of the impurity effects on two quantities in equation (16) according to figure 9(a).The impurity effects on the nonlinear gradient temperature gradient are likely to be dominated by linear effects.As the only factor causing upshift,the zonal flow is weakly affected by impurities,which is consistent with the conclusion of [14].

In addition,the fitting line of R0/Lnz=-8.88 does not extend to 18% in the same way as the other fitting lines because the downshift of the critical temperature gradient by impurities seems to be limited to R0/LT≃ 4,which is close to linear critical temperature gradient.As shown in figure 9(a),we cannot find quenched cases with parameters fz=18%,R0/Lnz=-8.88 within a time duration of 3000a0/cs0.The turbulence with a lower temperature gradient than R0/LT=4 is likely to be driven mainly by the impurity density gradient.The heat diffusivities in such cases have decreased to a lower level of about,which is about the magnitude of the neoclassical transport level[31,32].We speculate that for plasmas operating near the critical gradient,the addition of outwardly peaked impurities may reduce the temperature gradient,but the reduction is limited up to a linear critical temperature gradient with a modest heating power.

The red line in figure 9(b) is the connection of the ExFC data points in figure 3.The heat diffusivities of the unquenched cases near critical temperature gradients with outwardly and inwardly peaked profiles are shown here as well.Figure 9(b) presents a more complete picture of the impurity effects on the confinement.The outwardly peaked impurity can degrade the critical temperature gradient and cause a stronger heat flux near the critical temperature gradient,but the enhancement of heat diffusivity is weakened under a larger temperature gradient and even lower than the turbulence transport without impurities for profile relaxation,which corresponds to the conclusion in section 4.2.An inwardly peaked impurity can improve the confinement in terms of both critical temperature gradient and heat diffusivity.

5.Summary and discussion

In this work,we have investigated the effects of carbon impurities on ITG-driven turbulence transport with a collisionless limit and an adiabatic electrons assumption,based on the simulations of global fluid-type turbulence and transport code ExFC with a well-benchmarked four-field GLF model.The recombination and radiation of impurities are ignored.The impurity effects on the heat diffusivity of bulk ions and the critical temperature gradient are discussed in this work with parametric profiles of CBC,and the parameters are set according to experiments.

In summary,the effects of impurities on ITG-driven turbulence transport can be divided into two aspects.Firstly,an inwardly peaked impurity may improve the confinement by decreasing heat diffusivity and increasing the critical temperature gradient.Secondly,the nonlinear critical temperature gradient can be decreased by an outwardly peaked profile,but it cannot be further decreased for small heat diffusivity under a linear critical temperature gradient.It is worth mentioning that the impurity effects on the critical gradient are likely to be dominated by linear effects.Moreover,the destabilization effect of an outwardly peaked impurity is limited within a narrow temperature gradient region near the critical temperature gradient because the profile is relaxed quickly with a higher temperature gradient and decreases the transport level.The effects of inwardly and outwardly peaked impurity profiles on turbulence transport could be utilized to improve plasma confinement in tokamaks.

It is worthwhile to briefly discuss the importance of equilibrium profile relaxation in global nonlinear simulations.The simulations found a fast relaxation process of an outwardly peaked impurity profile within several milliseconds that usually makes the heat diffusivity lower than the case without impurities in a quasi-steady state.This is contrary to the linear and quasi-linear predictions for the same initial profile but consistent when the evolutions of density gradient are considered.Note that the simulations above have been performed under the assumption of a fixed temperature profile.The relaxation process of the temperature gradient may further change the result,particularly within the regime near the critical temperature gradient.In addition,ExFC can only simulate two kinds of ions at present,i.e.only one kind of impurity can be added in the simulation.However,there are many kinds of impurities in tokamak plasmas,e.g.,in the impurity seeding experiments,one or more kinds of ion (carbon,oxygen,etc.) already exist before seeding,but other kinds of impurities (neon,aluminum,etc.) are seeded in.To study phenomena in these experiments,simulations with multiple impurities are necessary.

Acknowledgments

The authors are grateful to Dr.Haotian Chen and Dr.Guangzhi Ren for very helpful discussions.This work was supported by National Natural Science Foundation of China(Nos.U1967206 and 12275071),National Key R &D Program of China (No.2017YFE0301201).The simulations were performed on HPC Platform of Southwestern Institute of Physics and Tianhe new generation supercomputer of National Supercomputer Center in Tianjin.