化归思想在苏科版初中数学中的实践应用

江苏省扬州市扬州大学数学科学学院(225000) 杨文轩 张波

初中数学是承接小学数学和高中数学学习的一个重要阶段,它最大的特点就是丰富学生对于数学学习的观念: 学习数学不仅仅是学习计算,更是学习证明等一系列逻辑关系.因此初中数学中蕴含着很多基本但又实用的数学思想方法,包括分类讨论、整体思想、化归思想等.阅读苏科版初中数学课本教材之后,可以发现无论在哪一年级,教材中的大部分知识都是在前一阶段的学习基础上进行深入学习,知识建构环环相扣.但当学生需要独立去处理一个综合问题或者是陌生问题时,无从下手的情况频频出现,难以将自己知识结构联系到题目中所考察的知识点.所以初中数学教师更应重视在教学活动中帮助学生提高数学思想的运用能力.而分类讨论、数形结合、函数方程等思想都衍生于化归思想,因此,着重在初中数学中渗透化归思想,可以帮助学生提高问题解决的能力,培养数学核心素养.

1 化归思想定义

“化归”一词来源于“转化”与“归结”,将一个问题删繁就简、从难到易、从一般到特殊、从特殊到一般的过程都称为化归.在数学中,我们反思解决数学问题的过程时,常常可以将待解决的陌生问题,转化为一个个小的熟悉的问题,或者是将一个很难的问题,根据“想要得到…”⇒“即要得到…”⇒“问题可转化为…”⇒“不妨设…”归结为一个容易的问题.数学解题的过程就是在不断拉近已知条件和待解决问题之间的距离,在这个过程中,陌生条件也会逐步转化为自己熟悉的知识点.它的哲学思想是指人们对于事物间的联系与矛盾都能够在一定条件进行能动的相互转化,运用了矛盾的同一性原理揭示了联系,实现转化.数学教师在进行知识传授时,应该重点带领学生体会如何将题目进行转化,就是我们常说的“我是怎么想到这么做的”,而不是具体的计算过程.

2 苏科教材文本分析

对苏科版初中数学教材从教材编排、内容选定、例题解答、课后习题四个方面进行阅读分析,发现化归思想在各个单元中都有所渗透.每学习一新的单元都可以在学生的认知结构中寻找到新知的“固着点”,任意层面中都体现了化归思想.从数的运算;代数式的运算;方程、函数、不等式以及图形与几何四个方面来论述化归思想在初中数学中的应用.

2.1 数的运算

在七年级数学的第一课是有理数的学习,它最大的特点就是将学生认知中的数域扩展到了实数域,在学习了绝对值与有理数的运算法则之后,学生可以将有理数的加减法转化为在此前小学阶段已经掌握的非负数加减法基础上的进一步学习,将有理数的乘除法转化为非负数乘除法基础上进一步深入,都体现出了化归思想.

例如: 计算-3×(-4)×6×(-7)×(-5)×3.

分析: 若学生直接计算,从左向右,由于因数较多,极易出现正负号的错误;学生在已经掌握了绝对值和运算法则的前提下,可以先根据负号的个数确定结果的正负号,将原式转化为3×4×6×7×5×3,先确定符号再将问题转化为正数相乘问题,负号的计算问题是初中数学抽象性的第一次体现,但对于此时很多初中生来说,他们的抽象思维还是刚刚起步,在上述例子中也只是用了整数进行说明,扩展到分数时,对学生的具象思维又是一种挑战.在实际教学中,这一步也一定要有所体现,帮助学生好好消化.

2.2 代数式的运算

代数式运算的本质其实还是实数运算,整式的加减法经过转化可以被归结为两个步骤: (i)去括号;(ii)合并同类项.单项式之间的相乘可以被转化为同底数幂的乘法或者是有理数间的乘法,即相同字母相乘、系数之间再相乘;单项式与多项式相乘、多项式与多项式相乘可以被转化为单项式与单项式相乘[2];分式的运算可以在掌握基本法则的基础上转化为整式的运算;推广到无理数的范围,其运算本质上也是有理数的运算;在整个代数运算的学习过程中,后一阶段的学习都是在前一阶段已经学习过的知识上进行的.

例如: 化简并求值: (x+2)(x-3)-x(2x-1),其中x=2.

分析: 题中要求先化简,即运用“化归法”化繁为简进而问题解决.多个整式的加减运算,去括号为第一步;接着合并同类项,同类项系数相加减就可归结成数的运算[3];注意区分字母和指数是解题要点,将复杂的整式转化为简单的数的加减形式,从而得到最简形式代入的值得到答案.

2.3 方程、函数、不等式

初中阶段关于函数的学习是与不等式和方程的学习息息相关的.解方程的本质就是在掌握等式的基本性质的基础上,将其转化为数和代数式的运算;分式方程也可以进一步转化为整式方程进行计算.

例如:ag 糖水中含有bg 糖(a＞b＞0).若再加入mg的糖,则糖水就会变甜.这一实际问题用不等式表示:____,如何证明这条结论呢?

图1

2.4 图形与几何

在初中阶段的平面几何学习中,三角形是最基础也最重要的.它不仅提供了定理、概念、性质等,而且为后续学习其他几何图形提供了研究方法与思路,例如平行四边形、梯形、相似、三角函数等,可以转化为三角形或在三角形中进行思考.究其根本,几何问题的证明几乎都是一个不断把问题向着某一定理或公理转化的过程,然后利用这个定理或公理解决问题.

例如: 如图2 所示,在梯形ABCD中,已知∠A+∠B=90°,点M、N分别为线段AB,CD的中点,求证:MN=.

图2

分析: 很多学生在看到这道题目的时候是不知所措的,很难立马看出题目中的条件所给的提示.运用化归的思想,我们可以想到将此梯形转化为三角形进行证明,经过思考,我们可以想到两种构造三角形的方法,一是延长AD与BC交于点E,再延长MN可证明得到延长线必经过E,构造出三角形;二是过点N分别作NE//AD,NF//BC分别交AB于点E、F(如图3) ;此处我们采取第二种方法为例.由已知条件∠A+∠B=90°,可得∠NEF+∠NFE=90°,因此ΔNEF是直角三角形.于是问题就转化为证明MN是RtΔNEF斜边上的中线,并且显然可得:AE=BF,EM=FM,M是EF的中点,故2MN=EF=AB-CD得证.

图3

3 初中数学教学中化归的常用方

3.1 分割法

顾名思义,“分割法”是把需要解决的问题分成若干个部分,并逐一进行求解,从而解决原问题的方法.在图形面积和几何体体积的计算或证明中,我们常用到分割法,通过对图形或几何体进行分割,以实现化归.

例如: 如图4,有一半圆形木板,其直径AB=18cm,现将此木板切割成以AB为下底的等腰梯形,上底CD的端点均在圆周上,且CD=9cm.求图4 中阴影部分的面积[4].

图4

分析: 阴影部分是弓形,初中阶段是没有学习过此类图形的计算公式,因此学生不能直接求解,所以我们需要借助辅助线对圆进行分割,则阴影部分面积就是扇形DOC的面积减去三角形DOC的面积.

3.2 变形法

变形法在初中阶段最主要的体现叫做恒等变形.再初中阶段的数学解题中占有非常重要的地位,主要应用于解方程和整除问题.如: 多项式、分式的恒等变形.解决问题时通过变形实现由未知到已知,由难道易,由繁到简的目的.

例如: 解方程:x4-x3-x2+x=0.

分析: 初中阶段没有学过四次方的求根公式或之类的直接解法,可以先把方程变形为:x2(x2-2x+1)+x(x2-2x+1)=0,即x(x-1)2(x+1)=0.进而求解.

3.3 映射法

映射法是目前化归思想中一种常用方法.映射指的是两个元素的集合之间,元素能够建立相互对应的关系,这一方法比其他的化归方法更加抽象.通过映射的原理,可以把亟待解决的问题向另一问题进行转化.例如,建立平面直角坐标系,可以让平面上的点与有序实数对对应起来,通过曲线和方程的对应关系,实现几何问题和代数问题的互化.

例如: 已知x1=2 是关于x的一元二次方程ax2+bx+c=3 的一个根,且二次函数y=ax2+bx+c函数图像的对称轴是直线x=2,则该函数图像的顶点坐标为______[5].

分析: 根据函数与方程的对应关系可知: 方程ax2+bx+c=3 的一个根为x1=2,可以转化为: 函数y=ax2+bx+c当自变量x=2 时,函数值y=3,即点(2,3)在该函数图像上,又因为函数的对称轴是直线x=2,则(2,3)为函数图像的顶点[6].

3.4 从特殊到一般

所谓从特殊到一般,即把一个特殊的数学问题想成一个更普遍的问题,把一个不一样的问题想成一个遇到过的问题,从而找到解决问题的办法.

分析: 乍一看运算繁琐,但也不难发现其中隐含的一般性质,可将式子中的2005 看作字母a,则原式:

代入a=2005,则答案为.

3.5 从一般到特殊

所谓从一般到特殊,就是首先以待求解问题的一个特殊情况为着眼点去思考和分析,找出该特殊情况和一般情况之间的关系,之后将问题中的一般情况进行转化为特殊情况去求解的一种解题方法.其实质就是找出这个问题的一个特殊状态(位置关系或数量关系),通过将变量替换为常量,将任意图形转化为特殊图形或特殊位置,数学研究可以在这一特殊状态下获得某种启发,这是特殊化的具体表现.

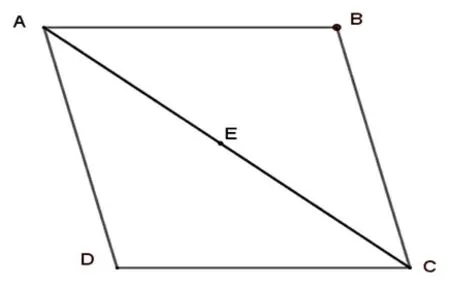
图5

A.ΔDEC与ΔAED的面积之和大于面积的二分之一

B.ΔBEC与ΔAED的面积之和大于面积的二分之一

C.ΔBEC与ΔDEC面积相等

D.ΔBEC与ΔDEC的面积之和等于ΔABE的面积

分析:E是对角线AC上的动点,若点E是AC中点,根据平行四边形的性质可以得出,点E也是BD的中点,即BE=DE.这时,B,D,E三点共线,所以点C到BE的距离与点C到DE的距离相等,即三角形BEC底边BE上的高和三角形DEC底边DE上的高相等,故三角形BEC与三角形DEC的面积相等.

在这一例题中,由E在AC中点上这一特殊情况,根据“等底等高的三角形面积相等”的性质和平行四边形的性质进行求解,其根本原理就是将求通解问题转化为求特解问题.在初中的数学的选择题中常采用特殊化法快速确定选项,但这一方法并不适用于所有问题,尤其是数学解答题,因此当我们采用一般问题向特殊问题转化的方法去解决问题时,需要根据题目条件具体问题具体分析.

结语

在初中数学教学活动中,融合化归思想不仅是贯彻新课程标准的要求,更是数学学科自身教学的需要.无论是在职教师还是准教师都应该深入理解化归思想的内涵,并结合初中数学知识以及学生的身心发展特征,从不同角度将化归思想融入教学中,以达到化抽象为具体、化复杂为简单、化模糊为清晰的教学目的.通过这种方法,这样可以帮助学生深入掌握数学知识,培养数学学科的核心能力.