L型加筋土挡墙地震动力响应理论分析
2024-03-14张晓曦任东兴何思明
彭 涛,张晓曦,柯 灵,任东兴,何思明
(1. 中冶成都勘察研究总院有限公司,四川 成都 610023; 2. 中国科学院、成都山地灾害与环境研究所,四川 成都 610299)
0 引言
L型挡土墙与加筋土属于柔性结构,具有良好的抗震性能,常用于地震多发区和高烈度区的支挡和支护工程中。L型挡土墙将墙体重量和踵板上填土重量相结合,共同抵抗填土推力作用[1]。当填土推力较大时,通常采用延长踵板长度,从而增加踵板上填土体积,提升挡土墙稳定性。加筋土是通过在土工结构物中铺设或打入土工合成材料、钢筋等筋材,以减轻土压力、增加边坡稳定性[2]。将加筋土结构应用于L型挡土墙中,充分利用各自优点,可减小墙后的土压力,提高挡土墙稳定性,或在安全系数不变的条件下,可减小踵板设计长度,从而减少踵板上填土体积,提高经济指标。
L型挡土墙的设计计算通常视墙体和踵板上填土为挡墙部分,土压力作用于通过踵板端部的竖直方向的假想墙背,采用该计算模型,DERUCHER等[3]分别应用Rankine和Coulomb土压力理论分析L型挡土墙静力稳定性问题,推导了坡顶荷载作用下主动和被动土压力系数;JO等[4-5]考虑墙体惯性力作用,根据Mononobe-Okabe法提出倒T型挡土墙动土压力计算方法,采用离心机试验验证了该计算模型,高估了踵板上填土重量,计算的稳定性偏高。对于短踵板式 L型挡土墙,通常将踵板端部和立臂顶部间的连线作为假想墙背,采用该计算模型,梁波等[6-7]采用Coulomb土压力理论,考虑水平冻胀力的影响,提出多年冻土区L型支挡结构的土压力计算方法。根据Rankine土压力理论或滑移线场理论可知,填土在自重作用下,两滑裂面间的夹角严格等于90°-φ,假想墙背取填土第二滑裂面,与竖直方向的夹角为45°-φ/2。应用该理论,EVANGELISTA等[8]提出了考虑地震水平加速度的Mohr应力圆分析法,即拟静力应力塑性法(new stress pseudostatic plasticity solution, NSPPS),用于计算L型挡土墙地震主动土压力;GRECO等[9-10]应用极限平衡理论建立地震荷载作用下短踵板式L型挡土墙临界状态方程,计算地震土压力系数与第二滑裂面位置。事实上,L型挡土墙滑裂面位置是与填土的物理力学参数、几何参数、加筋作用和地震外荷载等相关的变化量。戴自航等[11]利用非线性有限元分析软件ABAQUS,对基底摩擦系数折减,揭示了符合坦墙条件的L型挡土墙后填土中第一和第二滑裂面的位置,对不严格符合坦墙条件的L型挡土墙,其填土中可能出现第三滑裂面。蒋良潍等[12]基于拟静力法原理和地震角旋转,提出了地震工况下挡土墙的陡/坦墙判据及第二滑裂面倾角计算公式。何思明等[13]从能量的角度出发采用极限分析上限定理研究了坦墙第二滑裂面位置及重力式挡土墙地震稳定性问题。张晓曦等[1]提出了L型挡土墙长踵板式和短踵板式2种破坏模式,通过判据第三滑裂面是否出现,界定了2种破坏模式的临界条件。
加筋土属于柔性结构,允许产生较大变形,其良好的韧性可抵抗较大的地震水平惯性力作用。HUANG等[14-15]提出L型加筋土挡土墙结构,在考虑地基承载力的基础上,通过一系列平面应变模型试验,研究了L型挡土墙和加筋土L型挡土墙的失稳模式和地震动力特性,论证了该组合结构具有良好的抗震性能。本文应用极限分析运动学原理,建立地震临界屈服加速度系数表达式,研究地震荷载作用下L型加筋土挡墙的破坏模式与地震稳定性问题,分析筋材拉伸强度对2种破坏模式、滑裂面倾角和地震临界屈服加速度系数的影响。
1 L型加筋土挡墙破坏模式
L型加筋土挡墙破坏模式,根据判识是否出现第三滑裂面,将其定义为长踵板式和短踵板式,如图1所示。当踵板较长时,填土破坏出现2个滑裂面,即第一滑裂面AE和第二滑裂面AD,楔形滑块ADE将从填土顶面D点剪出,此时α<ρ,如图1(a)所示。当踵板较短时,填土破坏楔形滑块分为两部分,即楔形体CFD和AFDE,此时填土中出现3个滑裂面,即滑裂面AE、AF、FD,第二滑裂面AF出现在挡墙立壁中,第三滑裂面FD在填土顶面D点剪出,此时α>ρ,如图1(b)所示。α=ρ为长、短踵板的临界条件。根据滑移线场理论可知,长踵板式L型挡土墙在自重荷载作用下,α=β=45°-φ/2。根据土体运动相融性原则[16],对于短踵板L型加筋土挡墙,β=90°-θ。
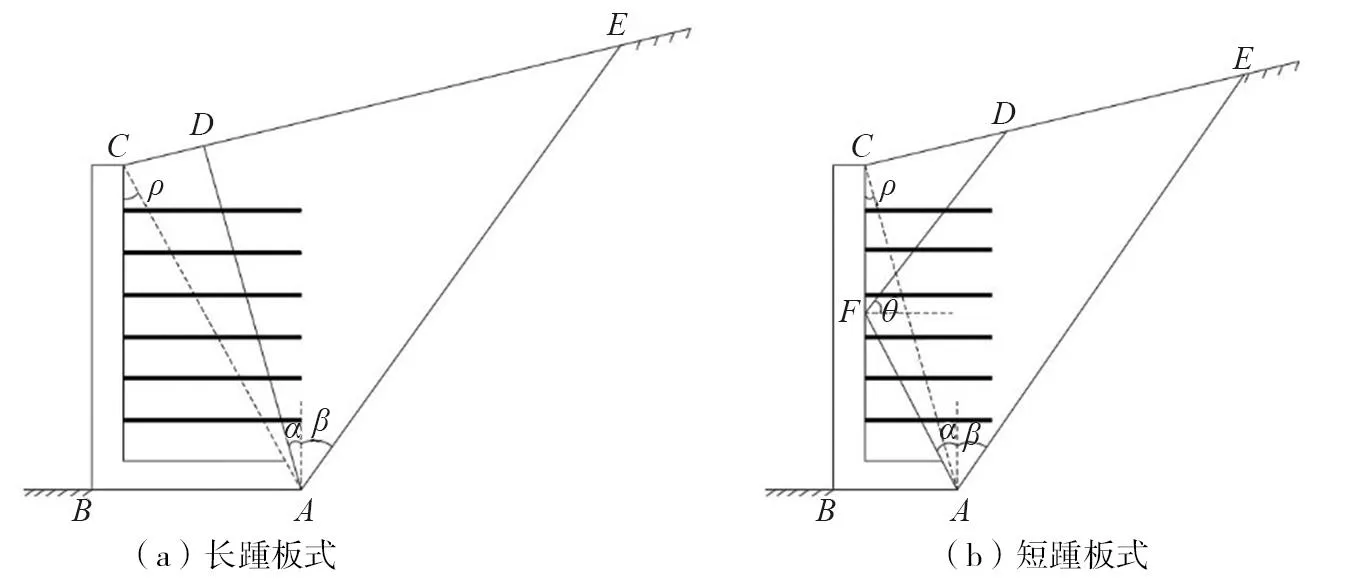
图1 L型加筋土挡墙破坏机制Fig.1 Failure mechanism of L-shaped of reinforced soil wall
在分析计算中做如下假设:①满足平面应变假设;②填土为各向均匀、同性和干燥的无黏性土;③遵守Mohr-Coulomb破坏准则,服从相关流动法则;④短踵板破坏模式满足土体运动相融性原则。
2 长踵板式破坏地震稳定性分析
地震荷载作用下,长踵板式L型加筋土挡墙计算模型如图2所示。抗滑部分包括L型挡墙墙体和填土abcD重量,加筋土筋材拉伸作用;滑动部分包括填土ADE和作用于墙体、填土上的水平地震力。滑动土楔沿着AD面滑动挤压墙体,筋材在AD面发生剪切作用。水平地震力采用拟静力法考虑,kh为水平地震加速度系数。L型挡墙墙体和填土abcD重量为Ww,所受水平地震力为khWw;滑动土楔ADE重量为Ws,所受水平地震力为khWs。滑裂面AE和AD与竖直平面的夹角分别为α和β。

图2 长踵板式L型加筋土挡墙计算简图Fig.2 Calculation diagram of L-shaped reinforced soil wall with long heel
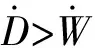
(1)

滑动土楔ADE所受外功率由自重Ws和水平地震力khWs提供,采用拟静力法考虑水平地震力,将地震惯性力作用于滑动土楔重心位置。则滑动土楔ADE所受的外功率表达式为
(2)
式中:φ为填土的内摩擦角;Vs为滑动土楔ADE的绝对速度。
墙体和抗滑土楔abcD所受外功率表达式为
(3)
式中:δb为挡墙踵板与地基土体间的摩擦角;Vw为墙体和抗滑土楔abcD的绝对速度。
加筋土筋材拉伸所作外功率可分为基于传统塑性理论上限法和基于广义塑性理论上限法。李秀娟等[2]将2种极限分析上限法用于加筋土结构稳定性分析并与离心机模型试验进行对比,发现2种方法计算结果相近,计算结果可靠,基于传统塑性理论上限法应用更为简单。
RADOSLAW[19]提出基于传统塑性理论的筋材拉伸所作外功率计算方法,假设筋材的破坏形式为拉伸破坏,外功率为筋材拉力在滑动层内所做的功。筋材加固作用在第二滑裂面AD上发挥作用,筋材加固所作外功率可以表示为
(4)
式中:l为滑裂面AD的长度;Vsw为滑动土楔ADE与墙体和抗滑土楔abcD在滑裂面AD上的相对速度;kt为单位截面上筋材拉伸强度,对于均匀分布的筋材,kt可表示为
kt=T/s=nT/(H-d)
(5)
式中:T为筋材拉伸强度;s为筋材层间距;n为加筋层数。
地震荷载作用下长踵板式L型加筋土挡墙速度相容场,根据速度相容场可绘制速度矢量三角形,如图3所示。根据正弦定理可知速度关系表达式为
(6)
式中:Vsw为楔形体ADE和楔形体abcD之间的相对速度。
将式(2)~式(4)代入到式(1)中,推导出地震水平加速度系数kh表达式为
(7)
式中:Ww和Ws可根据L型挡土墙的几何尺寸和材料重度计算得到;kt可根据筋材设计和筋材拉伸强度得到;将式(6)代入式(7)中可约掉Vs,因此式(7)是与填土滑裂面倾角α和β相关的函数,可通过数学迭代方法或最优化理论求得极值给出最优解,此时kh即为临界屈服加速度系数kc。

图3 长踵板式L型加筋土挡墙Fig.3 L-shaped reinforced soil wall with long heel
3 短踵板式破坏地震稳定性分析
当踵板较短时,L型加筋土挡墙出现第三滑裂面dD,此时滑动土楔分为两部分即AdDE和CdD,抗滑部分为挡墙墙体、填土abd和加筋土结构。
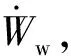
(8)
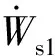
(9)
(10)

(11)
式中:Vs1为滑动土楔AdDE的绝对速度;Vs2为滑动土楔CdD的绝对速度;Vw为挡墙和填土abd的绝对速度。

图4 短踵板式L型加筋土挡墙计算简图Fig.4 Calculation diagram of L-shaped reinforced soil wall with short heel
与长踵板式L型加筋土挡墙破坏模式不同,由于第三滑裂面的出现,筋材拉伸在滑动层内所做的功分为两部分,分别为在第二滑裂面ad和第三滑裂面dD上所做的功。加筋土筋材拉伸在滑动层内所做的功为
(12)
式中:h为Bd的高度;Vs1w为墙体相对于滑动土楔AdDE的相对速度。
地震荷载作用下短踵板式L型挡墙速度相容场和相邻块体之间的速度矢量图,如图5所示。

图5 短踵板式L型加筋土挡墙Fig.5 L-shaped reinforced soil wall with short heel
在该计算模型中,块体AdDE、cdD分别与abd之间构成闭合的速度场。根据三角形正弦定理可知其速度关系式为
(13)
式中δ为挡土墙与填土之间的摩擦角。
将式(9)~式(13)代入到式(8)中,整理得到地震水平加速度系数kh的关系式为
(14)
由式(14)可知,在给定的L型加筋土挡墙尺寸和岩土物理力学参数条件下,水平地震加速度系数是关于滑裂面倾角α和β的函数,可通过数学迭代方法或最优化理论求得极值给出临界屈服加速度系数kc。
4 算例分析
L型加筋土挡墙采用砂性土填筑,墙高H=8.6 m,填土倾角η=0°,黏聚力c=0,内摩擦角φ=30°,墙-土摩擦角δ=10°,墙-地基摩擦角δb=30°,墙体厚度d=0.6 m,填土重度γs=18 kN/m3,墙体重度γc=24 kN/m3,如图6所示。

图6 L型加筋土挡墙算例Fig.6 Calculation example of L-shaped reinforced soil wall
为便于分析,引入无量纲参数λ和kt0,其表达式为
λ=(L-d)/(H-d)
(15)
kt0=kt/[γs(H-d)]
(16)
式中:kt0为单位截面筋材拉伸强度系数;λ为踵板长度系数,表示踵板长度与填土高度的比值。当踵板长度为长、短踵板式破坏的临界点时,可用λcr表示,称为踵板长度临界系数。
采用Mononobe-Okabe法和NSSPS法与本文计算L型挡墙地震屈服加速度系数进行对比,为了方便对比,建立L型挡墙的水平方向平衡方程,如图7所示,其表达式为

图7 L型挡土墙2种地震稳定性计算方法Fig.7 Two seismic stability calculation methods for L-shaped retaining walls
khWw+PAEcosφ=(Ww+PAEsinφ)tanδb
(17)
khWw+Sah=(Ww+Sav)tanδb
(18)
式中:PAE为挡墙地震主动土压力,该值可通过Mononobe-Okabe公式给出;Sah和Sav为挡墙地震主动土压力水平和竖直分量,该值可通过应力塑性法(NSSPS)给出。
采用Mononobe-Okabe法和应力塑性法计算地震荷载作用下L型挡墙临界屈服加速度系数并与本文计算方法进行对比,如图8所示。由图可知:临界屈服加速度系数随着踵板长度的增大而增大;长踵板式临界屈服加速度系数kc采用3种方法几乎相同;随着踵板长度的减小,挡墙破坏模式由长踵板式变为短踵板式;短踵板式临界屈服加速度系数Mononobe-Okabe法大于应力塑性法,且都大于本文方法;应力塑性法和Mononobe-Okabe法无法考虑墙-土摩擦角δ的影响,随着墙-土摩擦角δ的增大,本文方法逐渐趋近于应力塑性法;Mononobe-Okabe法和应力塑性法不能计算临界屈服加速度系数所对应的填土滑裂面倾角。
采用坦墙判别法和本文方法计算L型加筋土挡墙第二滑裂面倾角,如图9所示。由图可知:长踵板式破坏,采用本文方法与坦墙判别法计算第二滑裂面倾角几乎相同;随着踵板长度的增加,第二滑裂面倾角逐渐减小;短踵板式破坏,采用本文方法计算第二滑裂面倾角随着踵板长度的增大,先增大后减小,随着墙-土摩擦角δ的增大而减小;坦墙判别法计算第二滑裂面倾角随着踵板长度的增大而减小,该方法没有考虑墙-土摩擦角和第三滑裂面的出现,不适用于短踵板式破坏条件下第二破裂面预测。

图8 不同算法L型挡墙临界屈服加速度系数对比

图9 不同算法L型挡墙第二滑裂面倾角对比
临界屈服加速度系数kc、对应的填土滑裂面倾角(α,β)与单位截面筋材拉伸强度系数kt0之间的关系曲线,如图10~图12所示。
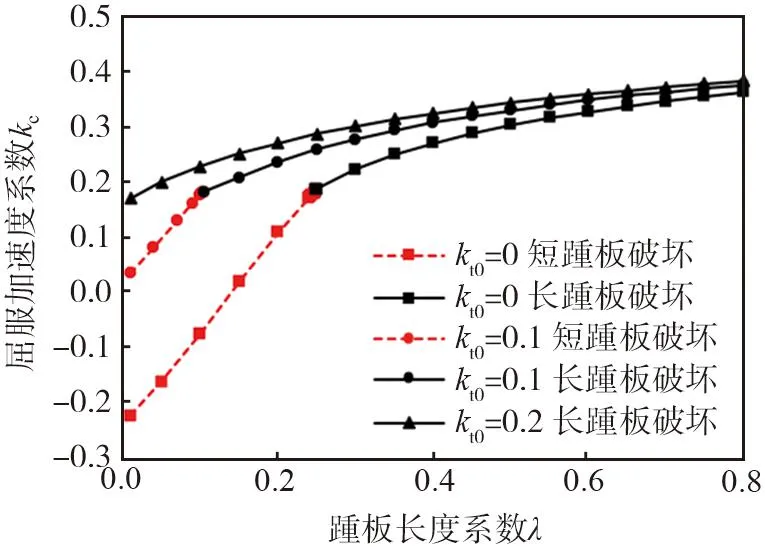
图10 临界屈服加速度系数与单位截面筋材拉伸强度系数关系曲线
图10给出了L型加筋土挡墙踵板长度系数λ从0~0.8之间变化单位截面筋材拉伸强度kt0分别为0,0.1,0.2条件下,临界屈服加速度系数kc曲线。计算结果表明:随着踵板长度系数λ的减小,临界屈服加速度系数kc逐渐减小,进入短踵板式破坏后下降趋势增大;随着单位截面筋材拉伸强度系数kt0增大,临界屈服加速度系数kc增大,短踵板式破坏增大幅度大,这说明加筋作用对短踵板式L型挡墙的加固效果更为明显;随着单位截面筋材拉伸强度系数kt0增大,长、短踵板破坏的临界点减小,即踵板长度临界系数λcr减小,当kt0=0.2时,不出现短踵板式破坏。
对应的滑裂面倾角β与单位截面筋材拉伸强度系数kt0之间的关系曲线,如图11所示。计算结果表明:滑裂面倾角β随着单位截面筋材拉伸强度系数kt0的增大而增大,随着踵板长度系数λ的增大而增大,短踵板式破坏其增大趋势更明显。
对应的滑裂面倾角α与单位截面筋材拉伸强度系数kt0之间的关系曲线,如图12所示。计算结果表明:长踵板式滑裂面倾角α随着单位截面筋材拉伸强度系数kt0和踵板长度系数λ的增大而减小;短踵板式滑裂面倾角α随着单位截面筋材拉伸强度系数kt0的增大而减小,随着踵板长度系数λ的增大先减小后增大,当α=ρ时,为长、短踵板破坏模式的临界点。

图11 滑裂面倾角β与单位截面筋材拉伸强度系数关系曲线Fig.11 Effect of tensile strength coefficient of unit section reinforcement on inclination of sliding surface β图12 滑裂面倾角α与单位截面筋材拉伸强度系数关系曲线Fig.12 Effect of tensile strength coefficient of unit section reinforcement on inclination of sliding surface α
单位截面筋材拉伸强度系数kt0对踵板长度临界系数λcr及其对应的临界屈服加速度系数kc的影响,如图13和图14所示。由图13可知:L型加筋土挡墙踵板长度临界系数λcr随着单位截面筋材拉伸强度系数kt0和填土内摩擦角φ的增大而减小;当踵板长度临界系数等于0时,不发生短踵板式破坏。
由图14可知:在L型加筋土挡墙长、短踵板破坏临界位置,临界屈服加速度系数kc随着填土内摩擦角φ的增大而增大,随着单位截面筋材拉伸强度系数kt0的增大而减小,踵板越长下降趋势越明显,这是由于踵板较长时,挡墙稳定性主要由踵板上填土重量提供,踵板较短时,主要由筋材提供。
墙-地基摩擦角δb对踵板长度临界系数λcr及其对应的临界屈服加速度系数kc的影响,如图15和图16所示。由图可知:踵板长度临界系数λcr随着墙-地基摩擦角δb和填土倾角η的增大而减小,填土倾角η对长、短踵板破坏临界位置影响很小,几乎可以忽略;在L型加筋土挡墙长、短踵板破坏临界位置,临界屈服加速度系数kc随着墙-地基摩擦角δb的增大而增大,随着填土倾角η的增大而减小。

图15 踵板长度临界系数与墙-地基摩擦角关系曲线Fig.15 Effect of wall-base friction angle on critical length coefficient of heel slab图16 临界屈服加速度系数与墙-地基摩擦角关系曲线Fig.16 Effect of wall-base friction angle on critical yield acceleration coefficient
5 结论
L型挡墙和加筋土都属于柔性结构,具有良好的抗震性能,将筋材铺设于L型挡墙踵板上的填土中,增加第二破裂面抗滑特性,可减少踵板上填土重量,提高经济指标。本文根据第二、第三滑裂面产生条件,提出踵板长度临界系数λcr,以界定长踵板式和短踵板式2种破坏模式。应用极限分析上限定理,分别建立2种破坏模式下L型加筋土挡墙临界状态方程,推导其地震屈服加速度系数,针对其地震动力稳定性和长、短踵板破坏模式的临界条件进行了探讨,并得到以下主要结论:
1)地震荷载作用下L型挡墙,本文方法与Mononobe-Okabe法和应力塑性法计算的长踵板式破坏临界屈服加速系数kc几乎相同;短踵板式破坏Mononobe-Okabe法大于应力塑性法,都大于本文方法;随着墙-土摩擦角δ的增大,本文方法逐渐趋近于应力塑性法。
2)长踵板式破坏,采用本文方法与坦墙判别法计算第二滑裂面倾角几乎相同;短踵板式破坏则差别较大,这是由于坦墙判别法没有考虑墙-土摩擦角δ和第三滑裂面的出现。
3)加筋作用可有效地提高L型挡墙抗震稳定性,提高临界屈服加速度系数,改变长、短踵板破坏模式;通过对加筋土拉伸强度的设计,可使破坏只发生长踵板式破坏。
4)L型加筋土挡墙屈服加速度系数kc随着筋材拉伸强度、踵板长度、填土内摩擦角、墙-土摩擦角和墙-地基摩擦角的增大而增大。
5)第二破裂面倾角β随着踵板长度和筋材拉伸强度的增大而增大,短踵板式增量更大;第一和第三破裂面倾角α,长踵板式随着踵板长度和筋材拉伸强度的增大而减小,短踵板式随着踵板长度的增大先增后减,随着筋材拉伸强度的增大而减小。
6)踵板长度临界系数λcr随着筋材拉伸强度、填土内摩擦角φ、墙-地基摩擦角δb和填土倾角η的增大而减小,填土倾角η对其影响较小,可忽略。
