近海大气环境下RC框架结构时变地震易损性分析

郑山锁,徐玉海,杨 松,明 铭,可 亮

(1. 西安建筑科技大学 土木工程学院,陕西 西安 710055; 2. 西安建筑科技大学 结构工程与抗震教育部重点实验室,陕西 西安 710055)

0 引言

为促进近海地区的经济发展,满足近海资源勘探的需要,我国建造了大量近海工程[1]。然而,在近海大气环境的氯离子侵蚀作用下,不可避免地引发钢筋锈蚀,导致RC框架结构有效受力截面损失、承载力降低[1-2]。随着侵蚀作用加深,堆积于钢筋表面的锈蚀产物会引起钢筋沿纵向产生锈胀应力,使保护层混凝土处于复杂应力状态,造成混凝土性能劣化,并引起保护层开裂甚至脱落,进而导致RC框架结构抗震性能不断地劣化,安全性持续降低。

近年来,随着人们防灾、减灾意识的提高,越来越多的学者从试验和数值模拟角度陆续进行了氯离子侵蚀下RC框架结构抗震性能的研究工作。如:YALCINER等[3]对一栋因氯离子侵蚀而拆除的RC框架结构进行了易损性分析,模拟了因锈蚀而失去粘结强度的钢筋滑移对结构抗震性能的影响。AKIYAMA等[4]建立了基于氯离子锈蚀的RC桥墩纵向钢筋屈曲模型的位移延性能力评估方法,并对其可靠性进行评估。胡思聪等[5]构建了基于氯离子侵蚀作用下的RC桥梁材料劣化模型,获取并评估了近海大气RC桥梁时变抗震性能损伤规律。李超等[6]建立了与电流密度相关的氯离子锈蚀钢筋模型,以预测近海桥梁结构抗震性能变化规律。

上述研究结果在一定程度上丰富和加深了人们对锈蚀结构抗震性能的认识,然而这些研究在分析时,一方面忽略了保护层开裂后,由于有害离子更易于侵入而引发钢筋锈蚀速率的增加,这显然高估了锈蚀结构的抗震性能。另一方面为便于分析,工程结构的安全评估通常仅考虑地震动不确定性,而假定结构分析模型参数为恒定值。然而已有研究表明[1]:当考虑结构响应的非线性行为时,与结构和地震动相关的不确定性耦合效应会放大,这意味着在评估结构的实际抗震性能时,考虑计算结构响应中的不确定性至关重要。此外,由于电化学腐蚀与自然条件腐蚀具有较大差异性,现阶段基于电化学腐蚀RC棱柱体试件轴压试验结果建立的针对于近海环境下RC框架结构约束混凝土性能劣化模型的准确性还需验证。为此,有必要基于合理的材料性能劣化模型,同时考虑结构与地震动不确定参数影响,针对近海大气环境下RC框架结构进行时变地震易损性分析。

基于此,本文结合氯离子侵蚀及钢筋锈蚀机理,提出了钢筋锈蚀速率三阶段时变模型。根据钢筋和混凝土材料退化机理,确定了适用于近海大气环境下材料性能劣化模型。在此基础上,根据解析易损性分析理论,建立近海大气环境下RC框架结构时变地震易损性分析框架。随后以一栋典型5层RC框架结构为研究对象,通过拉丁超立方抽样方法综合考虑结构与地震动参数的不确定性影响,建立结构-地震动分析样本库,通过增量动力分析法(increment dynamic analysis, IDA)方法,得到了结构时变地震易损性模型,绘制了4个龄期下的地震易损性曲线与易损性指数曲线,对其时变抗震性能进行评估。

1 钢筋锈蚀概率模型

近海大气环境下,氯离子对RC框架结构侵蚀过程可划分为3个阶段[7]:①诱导阶段。氯离子渗透混凝土保护层并在钢筋表面堆积,当达到临界浓度时,钢筋发生锈蚀。②发展阶段。随着钢筋锈蚀发展,保护层混凝土因钢筋锈胀而出现拉应力,直到保护层混凝土拉应力超过其极限拉应力,保护层混凝土开始出现裂缝。③劣化阶段。随着裂缝扩展,钢筋腐蚀速率加快,钢筋与混凝土力学特性发生劣化,结构性能明显退化。氯离子侵蚀过程如图1所示。鉴于此,建立氯离子侵蚀下钢筋与混凝土力学特性劣化模型,需要确定钢筋起锈时间与保护层混凝土锈胀开裂时间。

图1 氯离子侵蚀过程Fig.1 Chloride erosion process

1.1 钢筋起锈时间

由钢筋锈蚀机理可知,确定钢筋起锈时间,关键在于定量评估氯离子在混凝土中的渗透规律。CUI等[8]及COLLEPARDI等[9]基于Fick第二定律,建立相应扩散模型,模拟氯离子在RC框架结构的扩散过程。本文参考DURACRETE[10]提出的氯离子扩散时变模型,经简单转换,即可得钢筋起锈时间模型。该模型考虑了环境条件、测试方法及养护龄期等因素的影响,并且与实际氯离子扩散规律拟合效果良好,如式(1)所示:

(1)

式中:Ccr为尚未引发钢筋锈蚀的氯离子临界浓度;dc为混凝土保护层厚度;依据CECS 220—2007《混凝土结构耐久性评定标准》[11]提出的临界氯离子浓度,本文Ccr取值为1.3 kg/m3(C30混凝土);X1为Fick第二定律理想化模型假设引起的不确定性参数;ke为环境因子;kt为测试方法因子;kc为固化时间校正系数;m为服役期因子,取值为0.362;Cs为混凝土表面氯离子浓度;Ds为经验扩散系数;t0为经验扩散系数的参考龄期,取28 d;erf(·)为误差函数。其中,Cs与erf(·)可表示为

Cs=As(w/b)+εs

(2)

(3)

式中:w/b为水胶比;As和εs分别为与环境相关的系数。

考虑到氯离子扩散时变模型相关参数较大的变异性,DURACRETE[10]通过试验研究与统计分析,给出了上述时变模型各参数的概率分布规律,如表1所示。

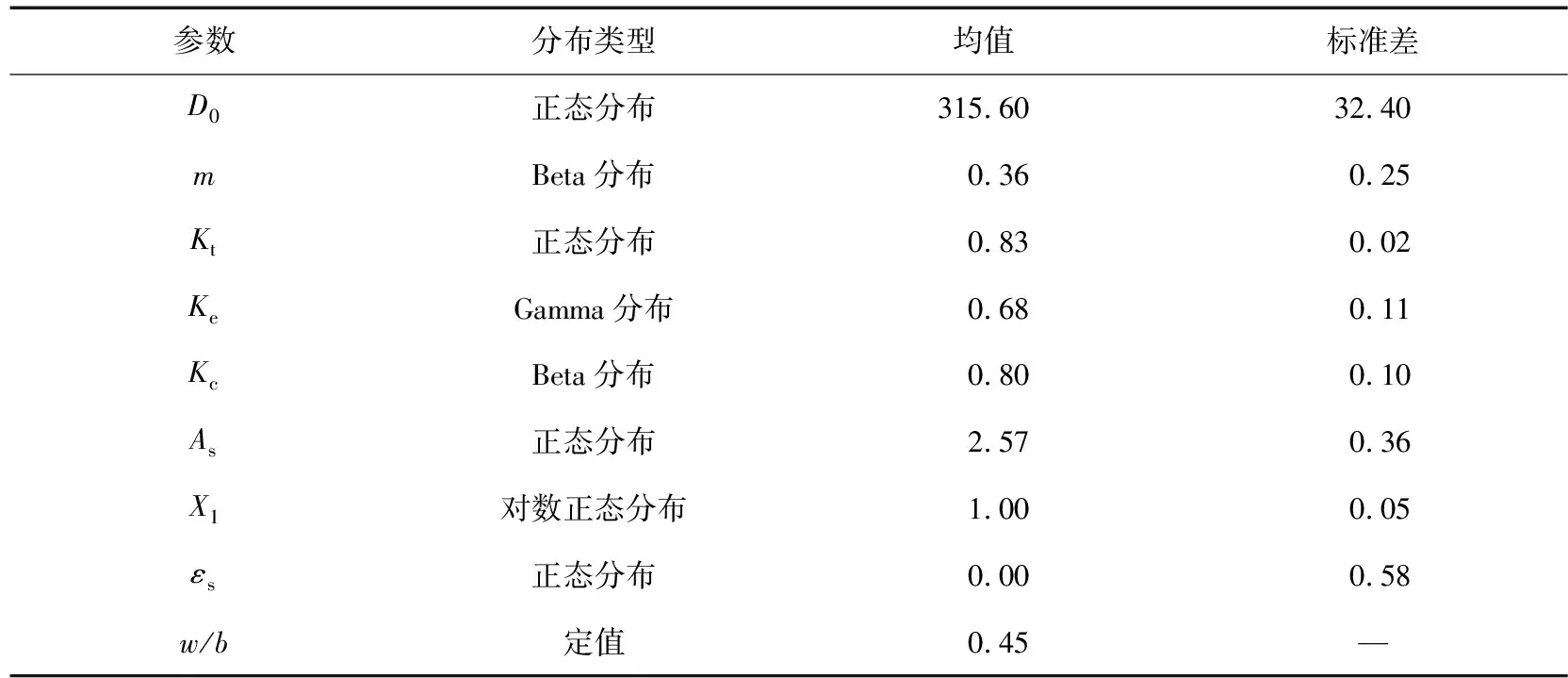
表1 各参数概率分布Table 1 Probability distribution of each parameter

1.2 保护层混凝土锈胀开裂时间

考虑到保护层混凝土锈胀开裂过程十分复杂,受多种因素影响,通常难以直接建立混凝土锈胀开裂时间预测模型,本文建立钢筋临界锈蚀深度与保护层混凝土开裂关系式为

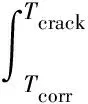
(4)

式中:Pcrack为钢筋临界锈蚀深度;Tcorr、Tcrack分别为钢筋起锈时间与保护层混凝土锈胀开裂时间;λ(t)为钢筋锈蚀速率,其为时间的函数。此外,CECS 220—2007《混凝土结构耐久性评定标准》[11]针对角部钢筋及非角部钢筋分别给出了钢筋临界锈蚀深度,表达式为

Pcrack=0.015(dc/d0)1.55+0.0014fcu+0.016

(5)

Pcrack=0.012(dc/d0)+0.00084fcu+0.018

(6)

式中fcu为混凝土抗压强度标准值(MPa)。

显而易见,建立保护层混凝土锈胀开裂时间预测模型的关键在于发展钢筋锈蚀速率模型。本文参考崔凤坤[7]提出的钢筋锈蚀速率三阶段时变模型,计算保护层混凝土的开裂时间。锈蚀速率模型示意图如图2所示,钢筋锈蚀速率三阶段时变模型如式(7)所示:

图2 三阶段时变锈蚀模型示意Fig.2 Three stage time varying corrosion model

(7)

式中:λ(t)为钢筋锈蚀速率,λi(t)为第i阶段钢筋锈蚀速率;twcrack为保护层混凝土严重开裂时间,本文取Twcrack等于Tcrack[12]。

icor(t)=0.85kσicor,0(t-tcorr)-0.29

(8)

icor,0=37.8(1-w/c)-1.64/dc

(9)

(10)

式中:icor(t)为钢筋锈蚀电流密度;icor,0为锈蚀起始时电流密度;Kσ为钢筋应力影响系数;w/c为混凝土水灰比;dc为混凝土保护层厚度;fyk为钢筋屈服强度标准值;σq为钢筋应力大小。

综上所述,保护层混凝土开裂时间模型可表示为

(11)

式中钢筋临界锈蚀深度可参考文献[11]确定,其余各参数说明与前文相同。

1.3 钢筋锈蚀率概率模型

钢筋锈蚀通常包括均匀锈蚀与点蚀。已有研究表明[13],近海大气环境下,点蚀是钢筋锈蚀的主要形式。考虑到钢筋点蚀形貌的多样性与复杂性,本文使用VAL等[14]提出的经典点蚀模型,如图3所示,通过使用简化四边形来模拟点蚀,以评估截面损失,点蚀下钢筋的相应时变残余截面积Acor可按式(12)～式(17)计算:

(12)

(13)

(14)

(15)

(16)

p(t)=Rλ(t)

(17)

式中:p(t)为锈坑深度,通过修正前文钢筋锈蚀速率λ(t)得到;ds0为钢筋初始直径;R为坑蚀系数,假设其符合极值I分布,利用统计分析方法计算[15],其余各参数说明与前文相同。

基于此,钢筋锈蚀率概率模型可表示为

(18)

式中:ηs(t)为钢筋锈蚀率;A0为钢筋初始面积,其余各参数说明与前文相同。

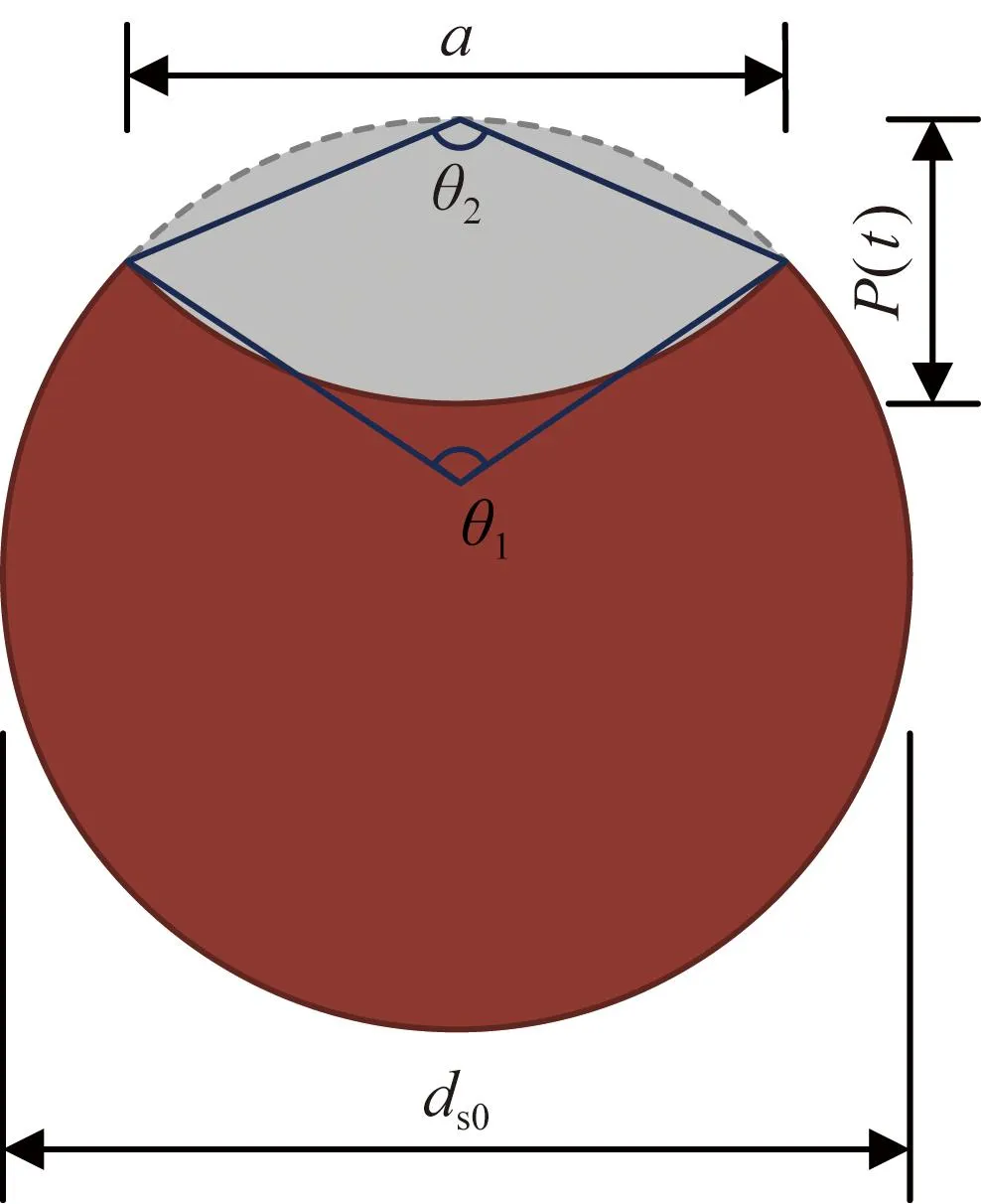
图3 点蚀模型示意[14]Fig.3 Schematic diagram of pitting corrosion model[14]

地震荷载及锈蚀作用的耦合作用会引起横向箍筋力学性能劣化及截面削弱,从而导致约束混凝土强度降低,甚至造成混凝土受力构件发生破坏。同时,在一般RC框架结构受力构件中,就保护层厚度及钢筋直径而言,横向箍筋均小于纵向钢筋,因此,横向箍筋的锈蚀速率将大于纵向钢筋锈蚀速率。然而,目前鲜有学者研究近海环境下箍筋的锈蚀。

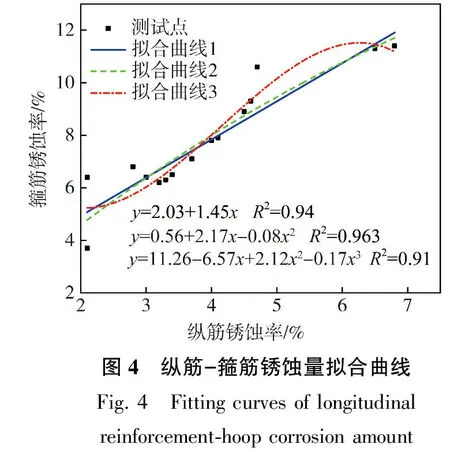
本文归纳总结了针对近海环境下钢筋锈蚀的21组试验数据[16-18],如表2所示,并利用Origin软件对数据进行回归拟合,对比分析横向箍筋和纵向钢筋之间的变化规律,如图4所示,并建立式(19)和式(20)拟合公式:

y=2.03+1.45x

(19)

y=0.56+2.17x-0.08x2

(20)

y=11.26-6.57x+2.12x2-0.17x3

(21)

式中:x为纵向钢筋锈蚀率(%);y为横向箍筋锈蚀率(%)。上述拟合公式的相关系数分别为0.940、0.963、0.910,可以得到,式(20)可较准确地表达近海大气环境下纵向钢筋锈蚀速率和横向箍筋锈蚀速率的相关关系,在此基础上构建近海环境下RC框架结构中纵向钢筋及横向箍筋锈蚀速率关系式为

y=a0+b0x+c0x2

(22)

式中a0、b0和c0均为拟合系数,可使用非线性曲线拟合分析确定取值。

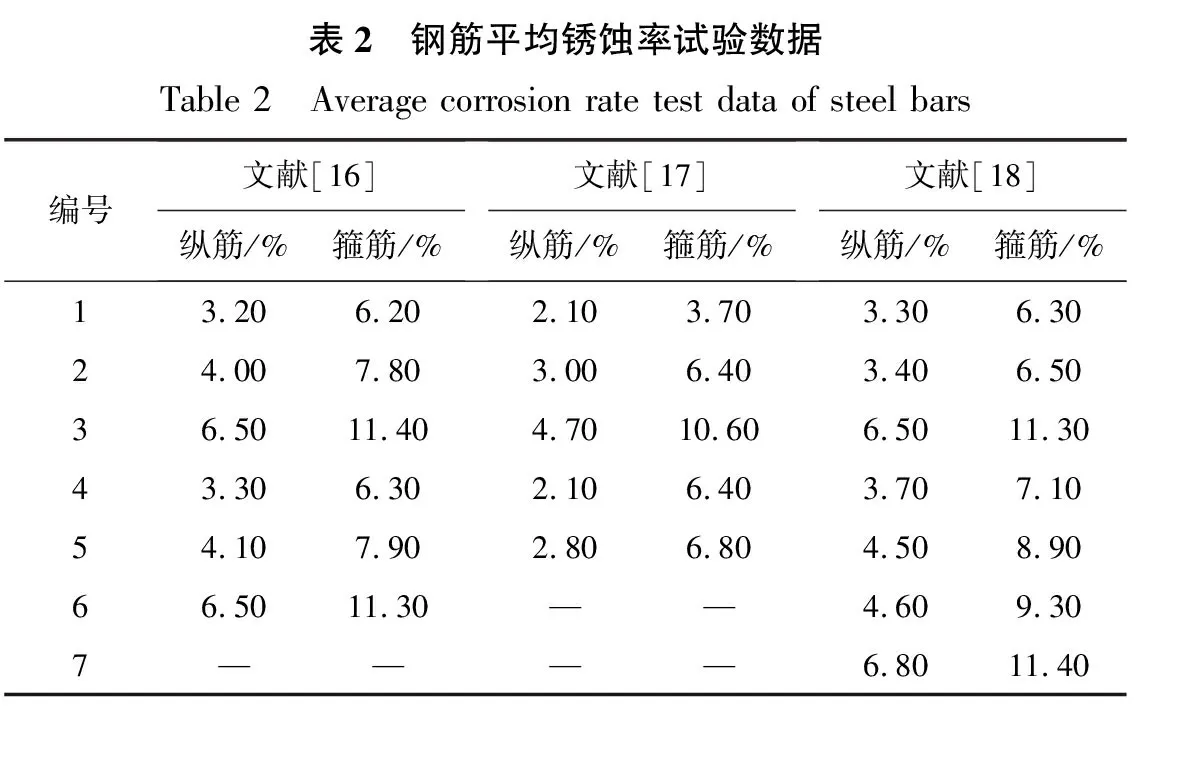
表2 钢筋平均锈蚀率试验数据Table 2 Average corrosion rate test data of steel bars编号文献[16]纵筋/%箍筋/%文献[17]纵筋/%箍筋/%文献[18]纵筋/%箍筋/%13.206.202.103.703.306.3024.007.803.006.403.406.5036.5011.404.7010.606.5011.3043.306.302.106.403.707.1054.107.902.806.804.508.9066.5011.30——4.609.307————6.8011.40 图4 纵筋-箍筋锈蚀量拟合曲线 Fig.4 Fitting curves of longitudinal reinforcement-hoop corrosion amount

1.4 材料性能劣化模型

钢筋锈蚀过程中,其强度和变形能力均发生不同程度地退化。BIONDINI等[19]基于试验结果,建立了锈蚀钢筋强度修正模型:

fyc=(1.0-αyηs)fy

(23)

fuc=(1.0-αuηs)fu

(24)

式中:fyc、fy分别为未锈蚀及锈蚀后钢筋屈服强度;fuc、fu分别为未锈蚀及锈蚀后钢筋极限强度;αy、αu为强度折减系数,一般取αy=0.0049、αu=0.0065[20];ηs为钢筋锈蚀率。

CAIRNS等[21]结合试验数据,建立了钢筋极限应变修正模型:

εuc=(1-αηs)εu

(25)

式中:εuc、εu分别为钢筋锈蚀前后的极限应变;α为应变折减系数,本文取α=0.01。

随着钢筋锈蚀产物不断累积,保护层混凝土逐渐锈胀开裂,进而导致保护层混凝体强度退化。本文参考CORONELLI等[22]研究,保护层混凝土的强度衰减表达式为

fc=ξfco

(26)

式中:fc、fco分别为保护层混凝土开裂前后强度;ξ为保护层混凝土轴心抗压强度折减系数。

(27)

wcr=2π(νrs-1)duni(t)

(28)

式中:P为试件周长;wcr为裂缝宽度,可按式(28)计算;vrs为钢筋锈蚀体积膨胀系数,取为2.0;duni(t)为钢筋锈蚀深度。

箍筋锈蚀显著降低了其对核心区混凝土的约束作用,导致核心区混凝土强度及变形能力发生退化。郑山锁等[23]基于锈蚀RC棱柱体试件轴压试验结果,认为箍筋锈蚀约束混凝土峰值应力f′cc与峰值应变ε′cc可按式(29)～式(30)计算:

f′cc=(1-0.017ηs)fcco

(29)

ε′cc=(1+0.01ηs)εcco

(30)

式中:fcco、εcco分别为未锈蚀试件峰值应力与峰值应变;ηs为箍筋锈蚀率。

1.5 模型验证

本文使用Menegotto-Pinto钢筋本构模型和Mander混凝土本构模型建立数值模型模拟文献[24-25]中的锈蚀RC框架柱,验证本文构建的钢筋锈蚀概率模型及材料性能劣化模型的准确性。由试验和数值模型模拟的滞回曲线对比验证结果(图5)及模拟结果与试验结果误差对比结果(表3)可知,本文构建的模型能较真实地反映锈蚀RC框架柱在循环荷载作用下的响应特征及抗震性能。

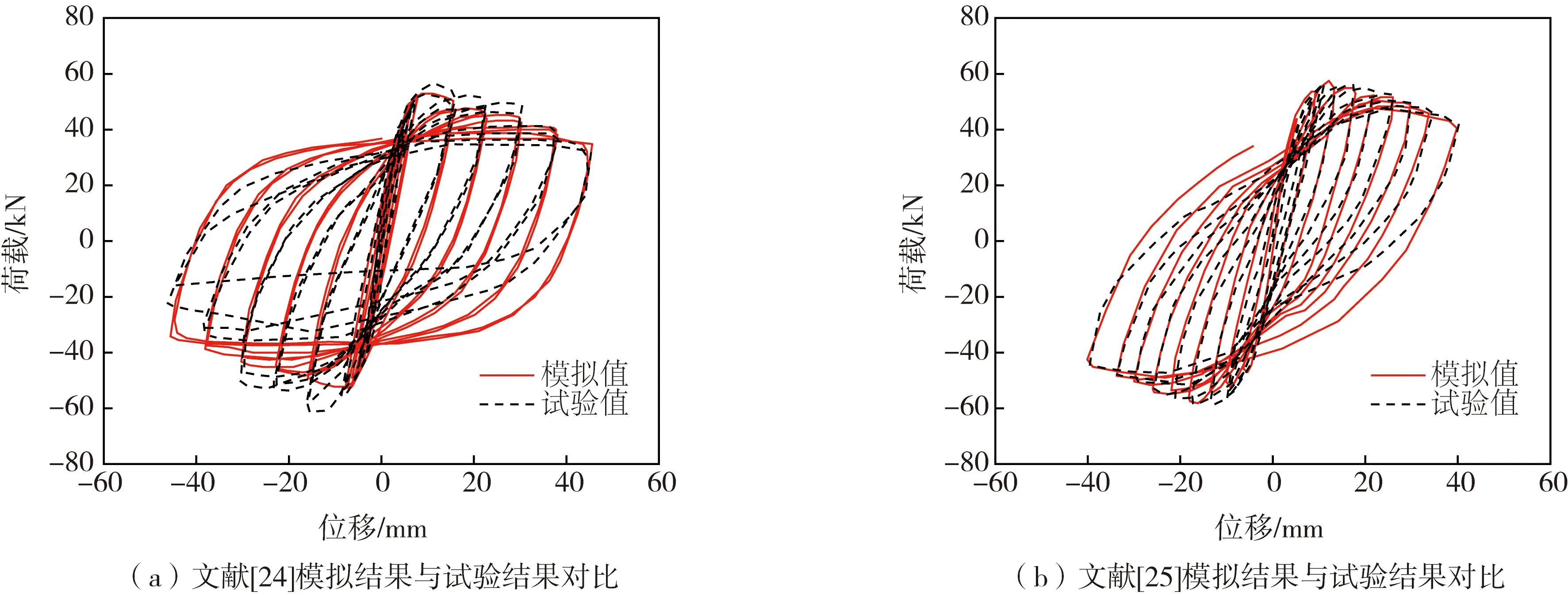
图5 滞回曲线模拟结果验证Fig.5 Results validation of hysteretic curves simulation

表3 模拟误差计算结果Table 3 Calculation results of simulation error

2 氯离子侵蚀的RC框架易损性分析方法

地震易损性分析的主要目的是得到不同强度地震作用下构件或结构体系地震响应达到或超过指定损伤状态的超越概率[26]。地震易损性函数的一般形式可以表示为[27]

(31)

式中:mD|IM和βD|IM分别为结构地震工程需求D的均值与对数标准差;mC和βC分别为不同极限状态下结构抗震能力C的均值与对数标准差。

其中,假定地震工程需求参数均值mD|IM和地震动强度指标IM之间满足幂指数式关系为

lnmD|IM=a+bln(IM)

(32)

式中a和b为统计回归系数。

地震工程需求参数对数标准差βD|IM表示为

(33)

式中,Di(i=1,2,……,N)为第i条地震波下结构地震需求;N为地震波数量。

针对传统易损性表达形式(如易损性曲线与易损性矩阵等)不便于工程应用等缺陷,于晓辉等[28]提出了易损性指数(vulnerability index, VI)的概念,尝试利用震害指数的数学期望评估结构地震损伤,可表示为

(34)

式中:DSi(i=1,2,…,n)对应为各极限状态的震害指数;Pf(DSi|IM)为结构各极限状态的超越概率,表示为相邻极限状态超越概率的差值,利用易损性曲线可得。

综合以上时变易损性分析机理及钢筋、混凝土材料退化机理,构建考虑氯离子侵蚀的RC框架时变易损性分析基本流程如图6所示。

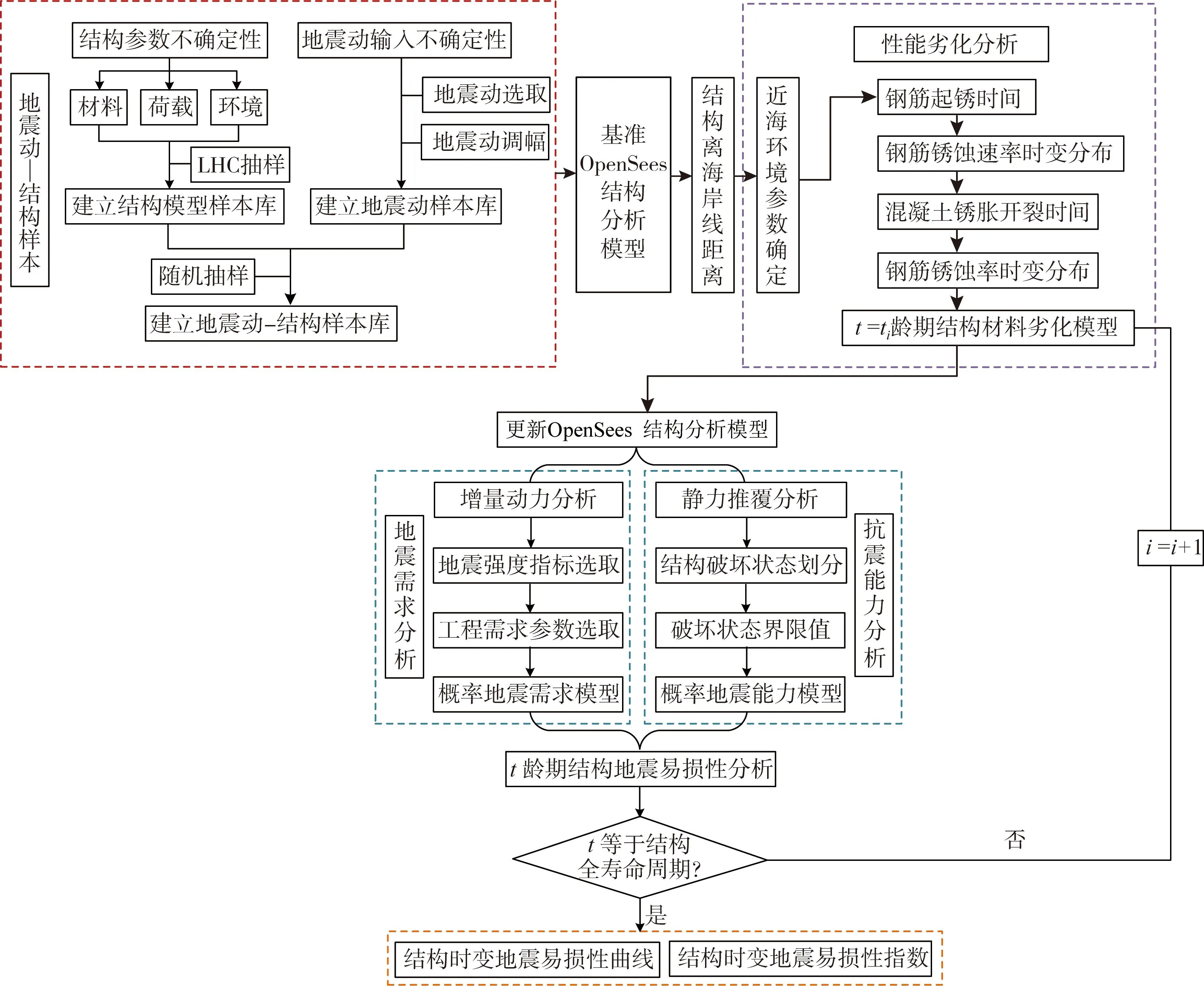
图6 结构时变地震易损性分析框架Fig.6 Framework of time-dependent seismic fragility analysis of structure

参考我国GB 50011—2010《建筑抗震设计规范》[29],并结合我国地震烈度表给出不同极限状态对应的震害指数值,如表4所示。

表4 不同破坏状态对应震害指数Table 4 Seismic damage index corresponding to different damage states %

3 算例分析

3.1 结构设计与建模

建立典型结构是研究区域RC框架结构地震易损性的基础。本章将利用PKPM软件构建一栋典型5层RC框架结构,结构设计满足我国GB 50011—2010《建筑抗震设计规范》[29]及GB 50010—2010《混凝土结构设计规范》[30]相关条例。结构布置如图7 (a)所示,平面尺寸为15.0 m×30.0 m,纵向5跨,横向3跨;首层高3.9 m,二至五层高3.3 m。结构抗震设计信息如下:结构位于抗震设防烈度8度(0.2g),地面粗糙度C类,特征周期0.4 s的场地区域。楼(屋)面恒、活载分别为7.0、2.0 kN/m2,该区域ω0=0.4 kN/m2、S0=0.3 kN/m2。采用OpenSees分析软件建立5层多龄期RC框架分析模型,其中梁、柱单元采用基于传统刚度法的Disp-Beam-Column单元模拟,为保证较高的精度,梁柱单元细分数取5,每个单元积分点数取5。考虑P-Delta效应影响。采用fiber、patch等命令定义的纤维截面建立梁、柱截面模型,该模型计算精度高且能较准确地反映结构实际受力情况。混凝土选用Concrete02材料,钢筋选用Steel02材料。梁柱单元和截面如图7(b)所示,材料本构关系如图7(c)所示。钢筋及箍筋分别采用HRB335及HPB300,混凝土采用C30。楼面及屋面板厚为120 mm;梁、柱保护层厚度为20 mm,梁柱尺寸及配筋结构如表5所示。

图7 结构布置及有限元模型Fig.7 Structural arrangement and finite element model

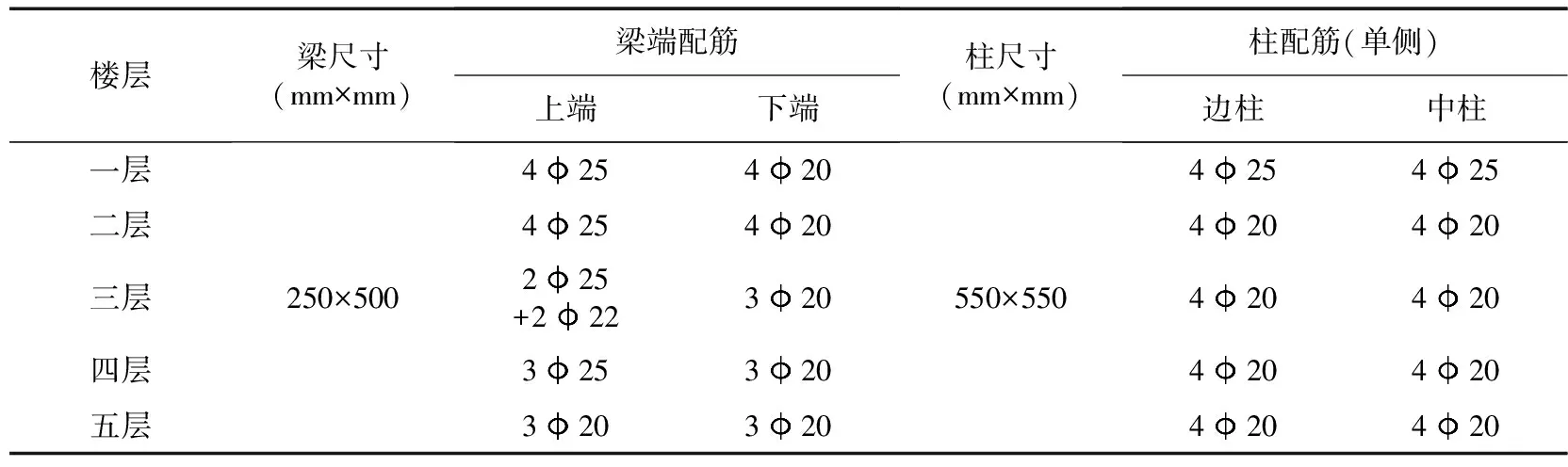
表5 框架梁柱截面尺寸及配筋Table 5 Frame beam-column section size and reinforcement

3.2 地震动-结构样本库建立

已有研究表明[31-32],采用20条地震动记录进行IDA分析可较好地解决由于地震动本身偶然性导致的易损性分析结果的不确定性。鉴于此,本文选取了美国应用技术委员会(applied technology council,ATC)建议的22条远场地震动记录[33],作为后续研究输入地震动,地震动记录详见文献[13]。所选地震加速度反应谱及对应的设计反应谱分布情况,如图8所示。由图可知,所选地震动记录平均反应谱曲线与规范反应谱曲线拟合较好,可用于评估RC框架结构在地震作用下的响应。

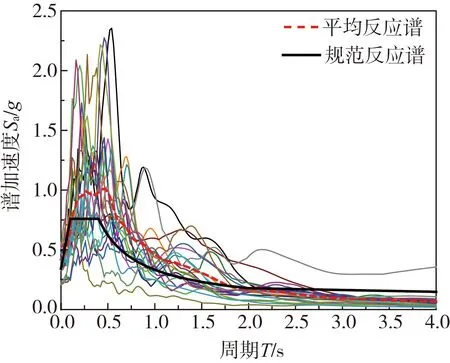
图8 所选地震动记录反应谱与规范设计 反应谱对比(ζ=0.05)Fig.8 Comparison between acceleration spectrum of selected ground motions and design response spectrum of Chinese code(ζ=0.05)

尽管有研究表明[13],结构不确定性对易损性分析结果的可靠性影响相对较小,在易损性分析中可不做考虑。然而当考虑结构响应的非线性行为时,与结构和地震相关的不确定性会耦合并放大。考虑到氯离子侵蚀在一定程度上增加了RC框架结构动力响应的非线性程度,本文在氯离子侵蚀RC框架结构时变地震易损性分析中,通过选取了结构几何属性与材料力学性能相关的15个随机参数作为设计变量,以考虑结构不确定性对氯离子侵蚀下RC框架结构易损性分析的影响,各设计变量的分布特征如表6所示。

根据表6中的结构不确定参数的分布特征,采用拉丁超立法抽样[34](Latin hypercube sampling, LHS),与随机抽样法生成多维结构样本空间,并与所选22条地震动记录进行随机匹配,得到22个结构-地震动随机样本。

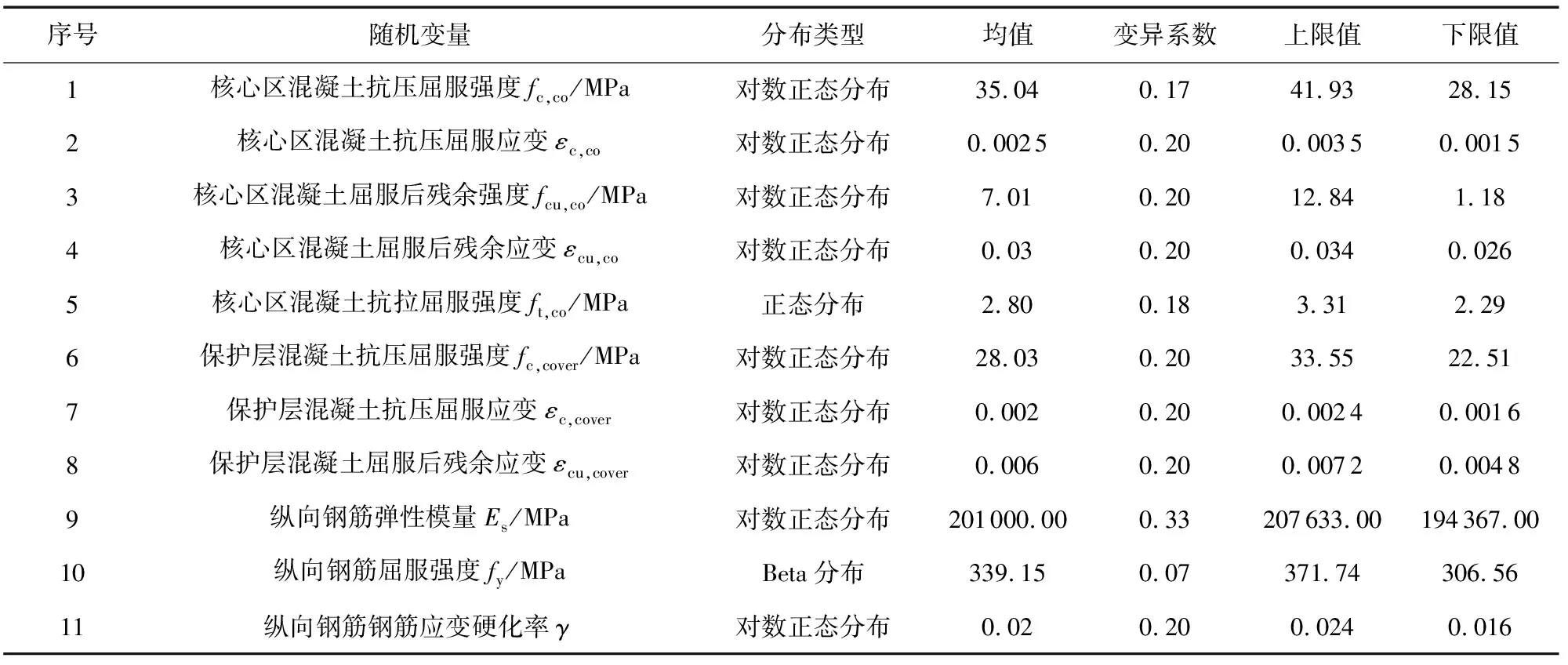
表6 结构不确定参数分布特征Table 6 Distribution characteristics of uncertain structural parameters

续表

3.3 结构材料劣化模型

结合表1中钢筋初始锈蚀模型各参数分布,通过LHS生成2000个样本,采用Origin软件获得LHS生成样本的频率分布和统计参数。计算得到钢筋起锈时间概率分布与保护层锈胀开始时间概率分布。由图9可知,不同直径钢筋锈蚀率与RC框架结构的服役时间呈正相关关系,但锈蚀速率与其呈负相关关系;相同服役龄期下,直径越小的钢筋,锈蚀程度越大。

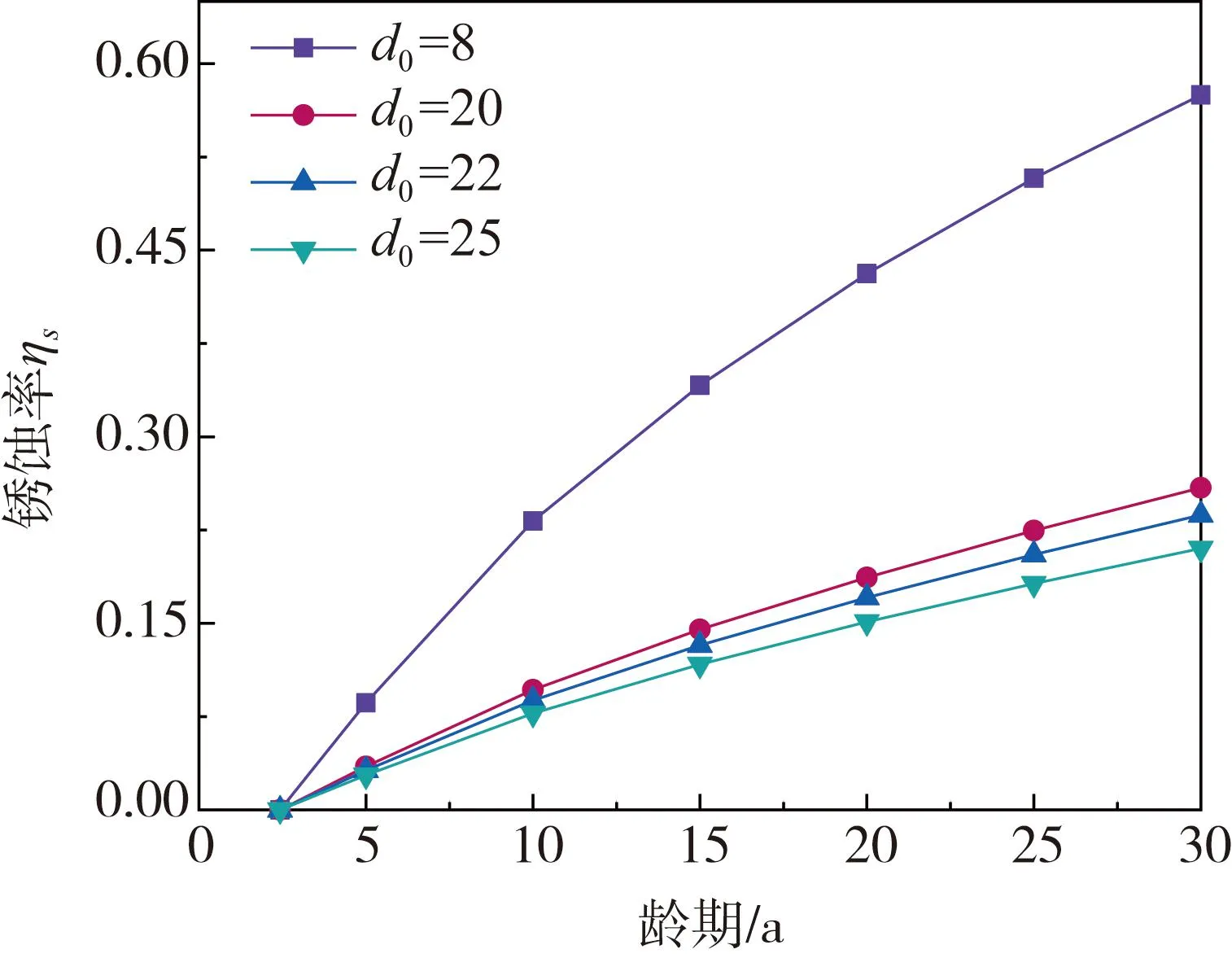
图9 钢筋锈蚀率时变规律Fig.9 Time-varying law of corrosion rate of steel bars

根据钢筋锈蚀率时变规律,结合钢筋混凝土材料性能劣化模型,进一步得到材料性能时变规律,如图10所示。由图可知,除约束混凝土峰值应变比值随龄期增加逐渐增大外,混凝土峰值应力比值、钢筋屈服强度比值、钢筋极限强度比值以及钢筋极限应变比值随龄期增加均呈现下降的趋势,且变化速率逐渐降低。

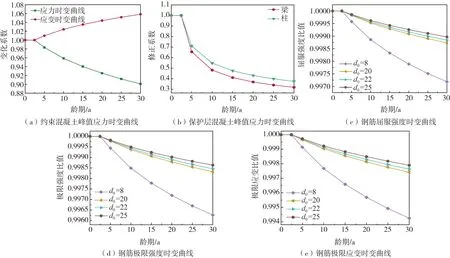
图10 材料性能时变规律Fig.10 Time-varying law of material properties

4 结构时变地震易损性

4.1 概率地震需求分析

本文使用PGA作为地震动强度指标,并将22条地震动PGA统一调整至0.018、0.1、0.15、0.22、0.40、0.51、0.62、1.0g。以最大层间位移角θmax为结构性能指标。通过对算例结构进行非线性时程分析,得到各服役龄期RC框架结构概率地震需求模型,其对数线性回归结果如图11所示。

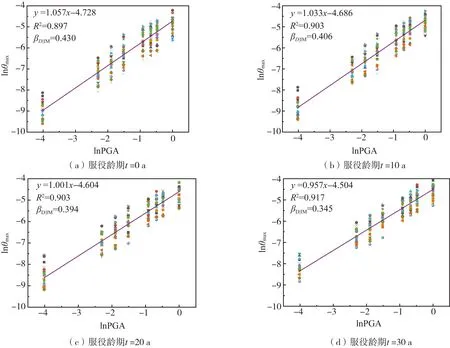
图11 概率地震需求模型对数线性回归Fig.11 Log-linear regression of probabilistic seismic demand model

4.2 概率抗震能力分析

GB 50011—2010《建筑抗震设计规范》[29]以层间位移角限值为破坏指标对应的各损伤状态下的对应位移角限值,如表7所示。

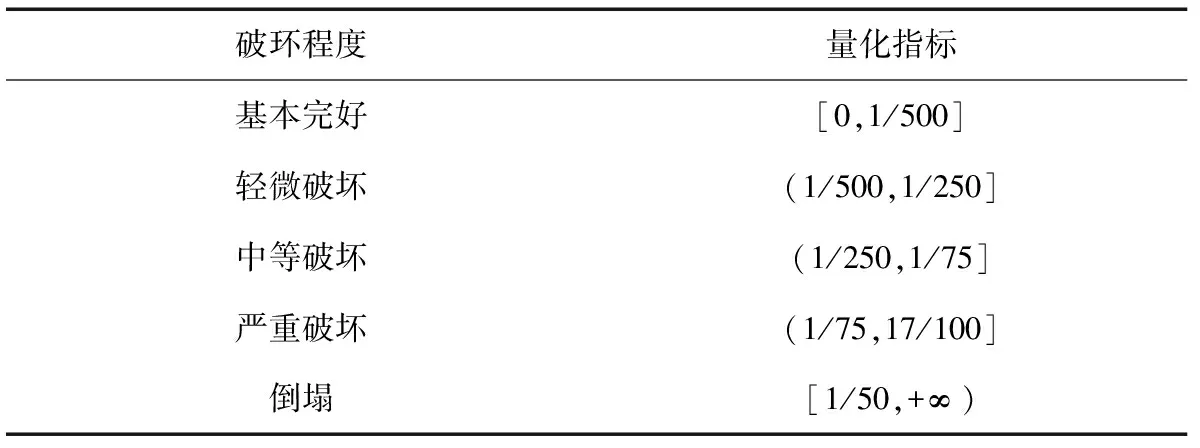
表7 框架结构的破坏描述和指标Table 7 Damage descriptions and indicators for a given frame structure

目前,对于RC框架结构的层间位移角限值的研究,多用于指导结构设计,均采取各破坏状态取值范围的下限,而本文研究的目的为评估结构在地震中的真实破坏状况,因而不能直接采取规范中建议的限值。同时本文假定锈蚀结构的抗震能力为恒定值。本文结合已有研究[35]GILL报告结果[36]提出建议的各破坏状态限值如表8所示。

表8 本文建议的各破坏状态的限值Table 8 Limits for each failure state recommended in this paper

4.3 概率地震易损性分析

为定量研究服役龄期对结构时变易损性的影响,得到结构时变易损性参数比较情况,如表9所示,随着结构服役龄期的增加,结构在不同损伤极限状态下的易损性函数均值(mR)与标准差(βR)呈现一定程度的下降趋势,表明结构的广义抗震能力逐渐降低,忽略龄期的影响,可能会高估结构的抗震性能。

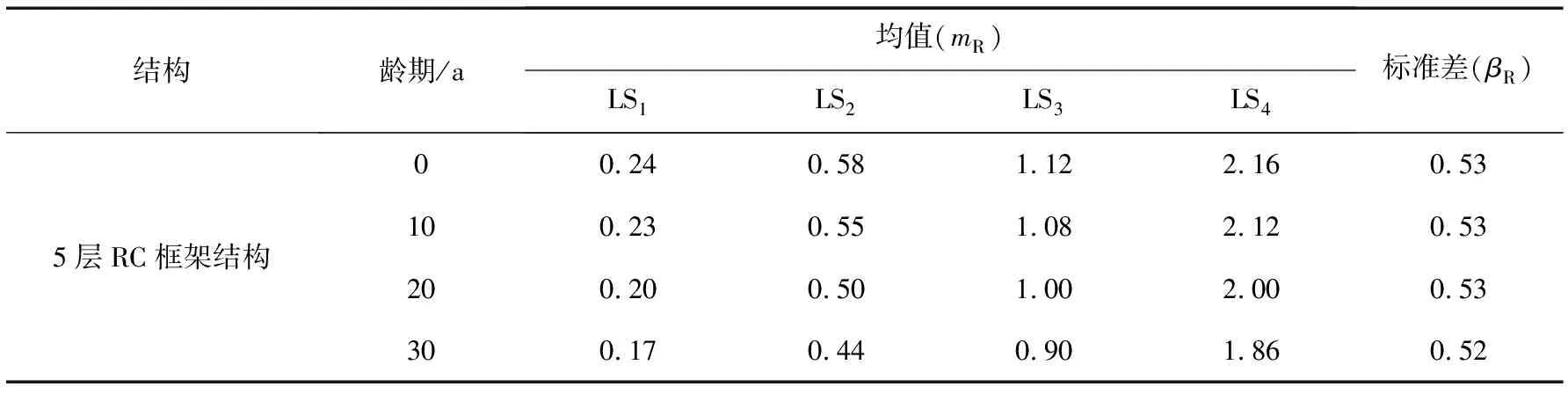
表9 不同服役龄期结构易损性函数参数Table 9 Structural vulnerability function parameters of different service ages

结合易损性函数参数分布,进一步得到近海大气环境下服役龄期分别为小于Tcorr、10、20、30 a的RC框架结构在各破坏状态下的时变易损性曲线,如图12所示,相同地震动强度下,结构各损伤状态的超越概率与服役龄期呈正相关关系,表明近海环境中的氯离子侵蚀效应会使得混凝土、钢筋材料的力学性能退化,导致梁、柱抗剪承载力降低,进而引发结构抗震性能降低。例如,对于地震动峰值加速度PGA=0.4g,未发生腐蚀(0 a)的结构达到中等损伤的概率小于26%,而30 a龄期的结构达到中等损伤的概率接近45%。不同损伤状态的超越概率随龄期的增加是非线性的,具体来说,前10 a的超越概率增加量相对较小,10 a后超越概率增加量明显增大。以中等损伤状态下的易损性曲线为例,当地震动峰值加速度PGA=0.6g时,10 a龄期结构的超越概率相对于未腐蚀结构增加了4.0%,20 a龄期的结构超越概率相对于10 a龄期结构增加了7.1%。由此可见,第二个10 a的超越概率增长率大约是前10 a的1.75倍。因此,在今后的结构抗震设计和评估中,对于恶劣坏境下的RC框架结构,有必要提高对结构服役环境和龄期的重视。

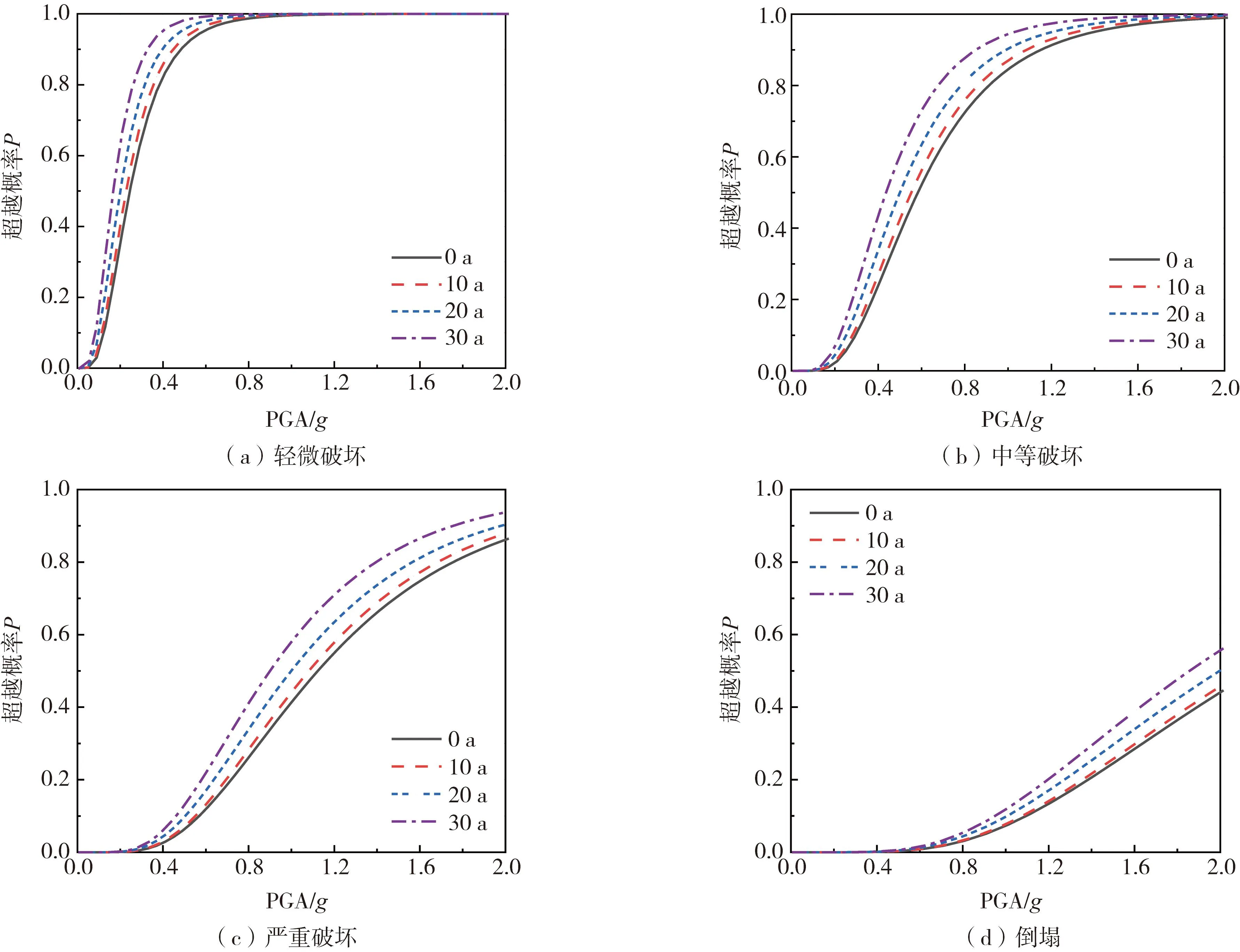
图12 不同损伤状态下的结构时变易损性曲线Fig.12 Time-varying fragility curves of structures under different damage states

4.4 结构损伤评估

基于前文计算得到的结构各极限破坏状态的超越概率,结合式(32)～式(34)以及表6中数据,计算得到各地震动强度下结构易损性指数,绘制出结构易损性指数曲线,如图13所示。为了更进一步评估结构的抗震性能,结合我国现行抗震规范提出的三性能抗震设防水准,本文分析计算出RC框架结构在多遇地震、设防地震及罕遇地震作用下的易损性指数分布规律,如图14所示。

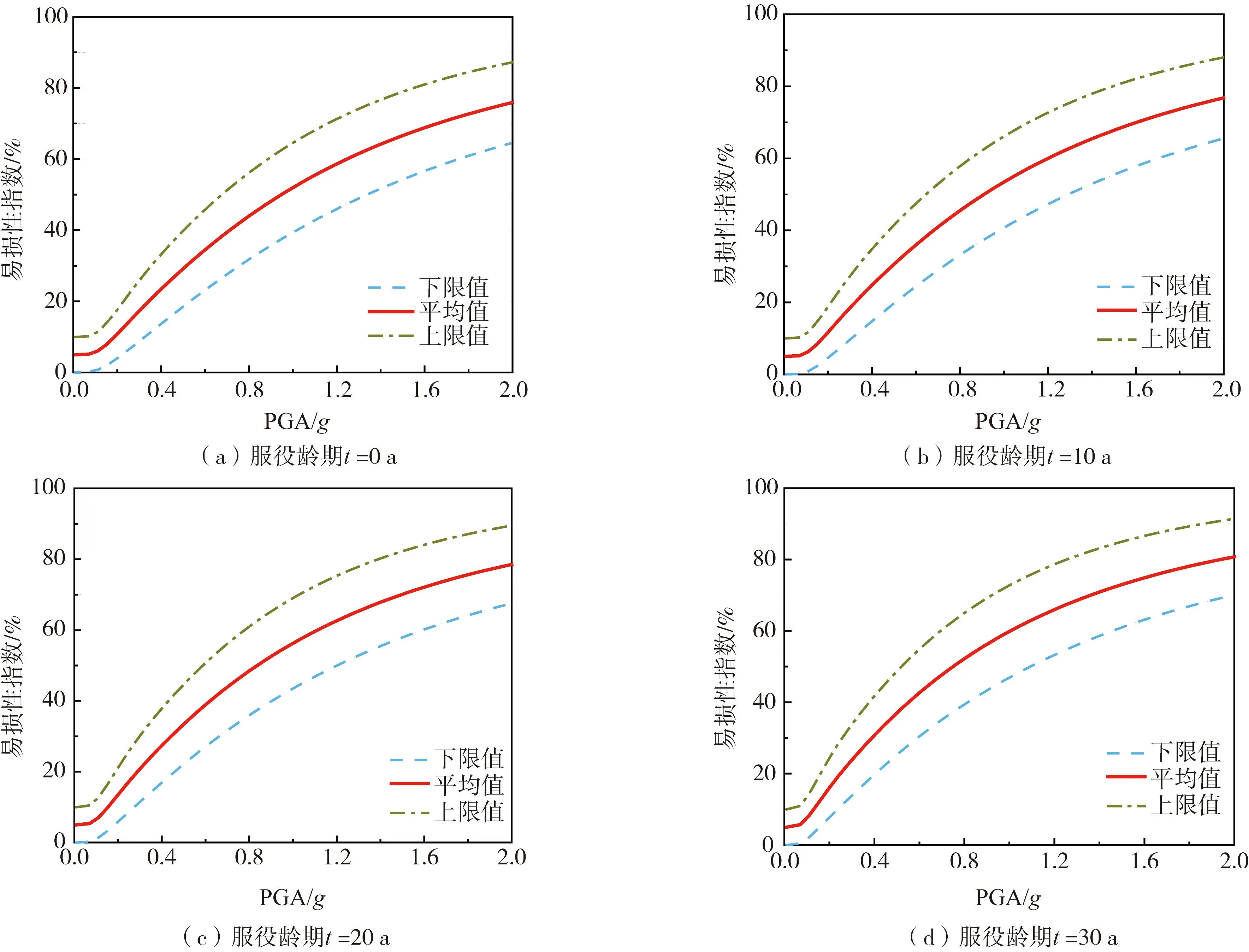
图13 易损性指数曲线Fig.13 Vulnerability index curves

由图14可知,当各服役龄期RC框架结构遭受多遇地震作用及设防地震作用时,若以易损性指数上限值和平均值作为评估标准,各RC框架均处于轻微破坏状态;若以易损性指数下限值作为评估标准,各RC框架均处于基本完好状态;但需指出,当不同服役龄期RC框架结构遭受罕遇地震作用时,若以易损性指数下限值作为基准评估结构破坏等级,各服役龄期结构均处于轻微破坏状态;若以易损性指数平均值作为基准评估结构破坏等级时,0、10、20 a龄期结构均处于轻微破坏,30 a龄期结构处于中等破坏;以易损性指数上限值作为损伤评估指标时,结构均处于中等破坏。

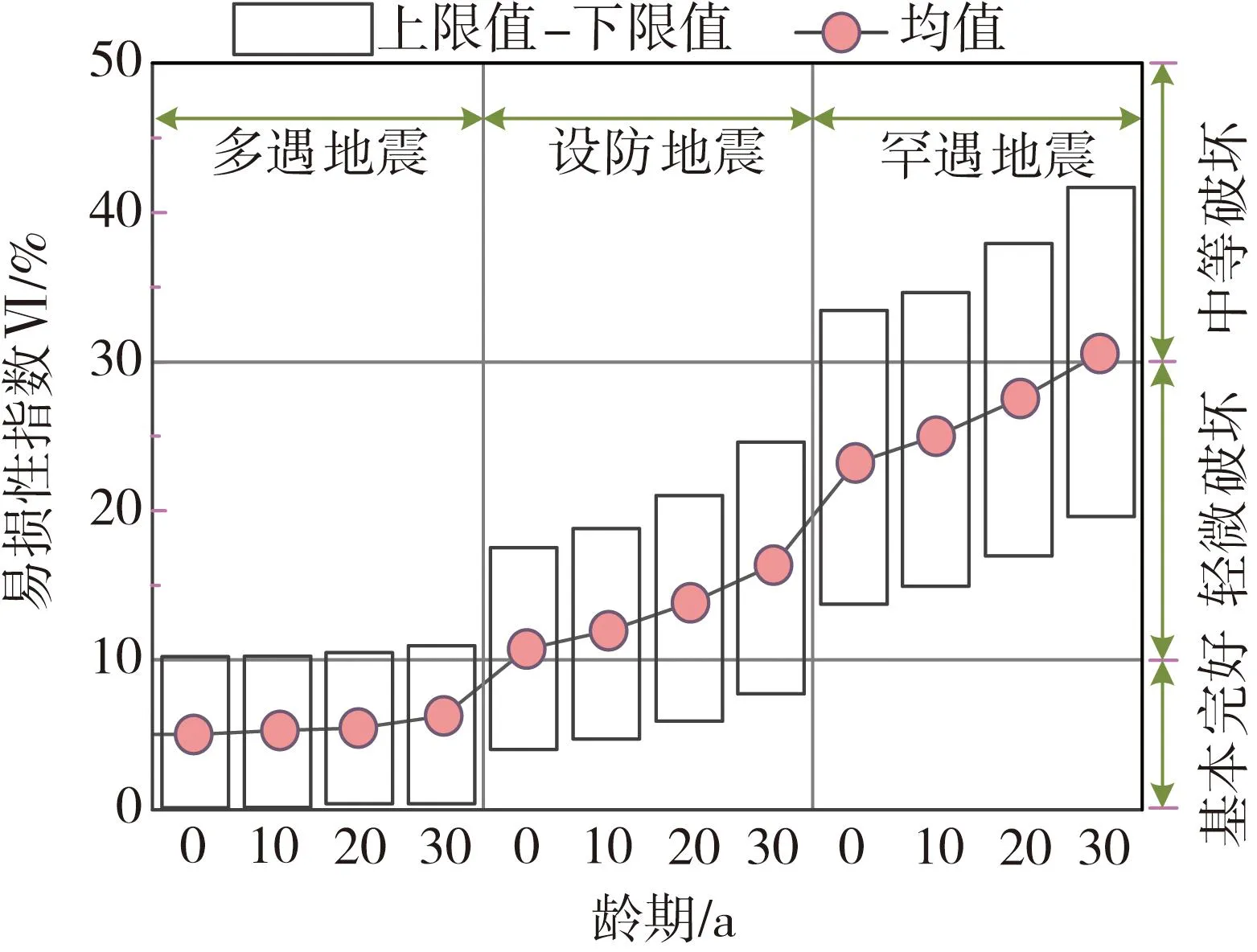
图14 三性能抗震设防水准下易损性指数分布Fig.14 Vulnerability index distribution under the three-property seismic fortification standard

由图14还可知,随着结构服役龄期的增加,结构在多遇地震、设防地震以及罕遇地震作用下的易损性指数均逐渐增大。这表明RC框架结构材料性能随着服役龄期增加不断劣化,结构抗震性能不断降低。但对于30 a服役龄期内的结构,无论是以何值作为结构损伤性能指标,在多遇地震与设防地震作用下,结构损伤程度不超过轻微破坏;在罕遇地震作用下,结构损伤程度不超过中等破坏。这表明按照我国规范设计RC框架结构,在30 a服役龄期内能够满足我国“小震不坏、中震可修、大震不倒”三性能抗震设防水准。

5 结论

本文根据氯离子侵蚀及钢筋锈蚀机理,提出了钢筋锈蚀速率三阶段时变模型,结合均匀锈蚀模型,提出一种改进的钢筋锈蚀率概率模型,进而根据材料性能退化机理,确定了适用于近海大气环境下的材料性能劣化模型。在此基础上,根据解析易损性分析理论,建立近海大气环境下RC框架结构时变地震易损性分析框架,并对时变易损性与损伤进行了评估。得到以下结论:

1)经过验证,本文基于氯离子第二扩散规律及钢筋锈蚀机理建立的钢筋锈蚀概率模型,更适用于近海大气环境且使多龄期RC框架结构地震易损性分析更加合理。

2)随着服役龄期的增加,结构在不同损伤极限状态下的易损性函数均值(mR)与标准差(βR)呈现一定程度的下降趋势,表明结构的广义抗震能力逐渐降低,忽略龄期的影响,可能会高估结构的抗震性能。

3)当地震动强度指标取值相同时,各损伤状态结构在服役龄期内的地震易损性呈现出非线性增大趋势。当地震动峰值加速度PGA=0.6g时,结构发生中等损伤状态的第二个10 a的超越概率增长率大约是前10 a的1.75倍。

4)以易损性指数作为结构损伤指标时,按照我国规范设计的RC框架结构,在30 a服役龄期内能够满足我国“小震不坏、中震可修、大震不倒”三性能抗震设防水准。