滑坡碎屑流消能桩结构动力计算与设计方法
2024-03-14李新坡孙玉莲吕珉昌
姚 军,李新坡,孙玉莲,吕珉昌
(1. 中国科学院、水利部成都山地灾害与环境研究所,四川 成都 610041; 2. 中国科学院大学,北京 101499)
0 引言
我国地域辽阔,山地面积宽广,导致地质灾害频发,滑坡是最常见的地质灾害,破坏性极大,并且难以实现精准的预测,往往对人们造成较大的伤害。滑坡碎屑流是由于滑坡失稳破坏后,在重力作用下向下运动形成一种离散的、破碎的、具有流体特征的碎屑流[1]。由于滑坡碎屑流的远程运动具有巨大的体积和能量,经常造成生命财产和基础设施的重大损失。
滑坡灾害形成的碎屑流,其运动特征表现为体积大、速度快和运动距离远,往往会对沿途的居民和基础设施造成巨大的破坏[2-3]。滑坡碎屑流的发生、运动机制是防护结构设计的基础,近年来逐渐成为国内外学者关注的对象,尤其是通过理论分析和模型试验对碎屑流的流动特征和运动特性的研究[4-8],使得人们对于碎屑流的认识越来越清晰,并且在此基础上,提出了一系列的防护措施。
基于防灾减灾的重要需求,近年来许多学者和工程技术人员在崩塌滑坡碎屑流防护结构和技术方面展开了大量研究,取得了较多的进展[9-14]。消能桩结构设置在滑坡碎屑流的运动路径上,可以降低崩塌滚石和碎屑流的运动速度,减小其运动距离和影响范围,从而降低灾害对下游建筑物的危害。此前的研究中,对滚石、滑坡或岩崩等形成的颗粒流的冲击力,以及影响冲击力因素的研究较多。FAUG等[15]、TAI等[16]通过室内模型试验研究了滑坡、岩崩灾害形成的巨大冲击力,建立了基于动量守恒的方程,从而推导挡墙上的时变力。JIANG等[17]在室内进行模型试验,分析颗粒流与挡土墙等防护结构相互作用时,挡土墙前堆积死区和颗粒流动层对冲击过程的影响,并且研究了颗粒流对挡土墙的冲击力计算。程谦恭等[18]以谢家店子滑坡碎屑流为例,对比分析了相同运动参数条件下的桩群防护结构对滑坡碎屑流运动产生的影响。结果表明,桩群防护结构对碎屑流具有明显的阻滞和耗能效应。LI等[19-22]采用数值模拟方法,研究分析了挡墙、桩群对滑坡体灾害的防护机制。RITCHIE[23]、何思明等[24-25]推导了滚石运动特性和冲击力的理论计算公式,验算崩塌滚石的冲击力。陈果等[26]基于三溪村滑坡,研究高位远程滑坡的速度和冲击力等关键因素与时程的演化关系。沈均等[27]利用桩-土材料的弹塑性性质,分析推导了消能桩在滚石冲击作用下的变形计算公式。
上述研究中,无论是运用数值模拟方法,还是理论计算方法,都只关注碎屑流的冲击特性和冲击力大小,对滑坡碎屑流冲击力的分布、消能桩的内力以及两者的动力作用计算考虑较少,尤其是消能结构内力对碎屑流动能耗散的计算,缺少可应用于实际的消能结构设计方案的研究。本文以此为基础,主要进行滑坡碎屑流的冲击力计算研究,推导得到碎屑流运动过程中的垂向速度分布,探究得到滑坡碎屑流对消能桩结构的冲击力分布计算模型,进而运用力法和功能定理计算消能桩的稳定性和挠曲变形。其中,消能桩的变形能和内力做功是碎屑流动能耗散的主要方式,基于此,结合稳定性验算得到消能桩消能量的理论计算模型。最后采用具体算例验证了该理论计算模型的可行性。
1 消能桩系统的基本原理
滑坡的防治主要分为主动防护和被动防护2种,主动防护包括加锚杆、锚喷记忆抗滑桩等,在危岩体发生破坏之前直接设置于危岩体上,与其融为整体,加强其稳定性,达到防止危岩体失稳破坏的目的;被动防护一般是在滑坡坡脚设置消能结构,如消能桩、拦挡结构等,被动防护主要通过消能结构耗散滑体的动能,或改变滑体的运动路径达到保护基础设施和人们生命安全的目的。消能桩结构是被动防护的一种,主要通过消能桩的变形、消能桩与碎屑流的碰撞、摩擦对滑坡碎屑流的动能进行耗散,减小滑坡的冲击能量和影响范围,从而达到降低目标风险的作用。消能结构一般布置在滑坡影响范围的中下游,如图1所示,施工条件优于高位滑坡体的主动加固工程,在高位滑坡风险防控方面具有较大的工程应用价值。当碎屑流冲击消能桩时,桩体发生变形产生抗弯反力作用于碎屑流,以此耗散碎屑流的动能,从而达到消能的目的。本文将探讨当消能桩锚固于基岩且不考虑岩土体的变形时,消能桩对滑坡碎屑流的消能计算过程。
将地面以上的消能桩简化为悬臂梁结构,在冲击力作用下悬臂梁会发生挠曲变形,并且产生抗弯反力,反力在消能桩与碎屑流相互作用整个过程中做功消耗滑坡碎屑流的动能,如图2所示。在这个过程中,消能桩的反力大小与分布的计算、反力作用的时间和距离,以及分布式冲击力作用下消能桩的变形是消能计算的重要环节,因此,本文将研究滑坡碎屑流冲击力的分布、冲击力做功以及消能桩的变形计算模型,并以此提出消能桩的设计方法。
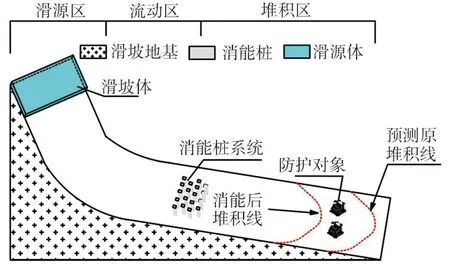
图1 消能桩布设示意图

图2 消能桩结构示意图
2 动力作用解析计算模型
2.1 冲击载荷演变过程
消能桩的挠曲变形和抗弯反力是计算其消能量的前提,碎屑流对消能桩的冲击力是设计的关键。根据YANG等[28]在碎屑流对刚性结构冲击力的数值模拟研究中表明,碎屑流冲击消能桩的冲击力变化可以概述为压力相对集中段,峰值型分布段和稳定抛物线型分布段3个阶段,如图3所示。
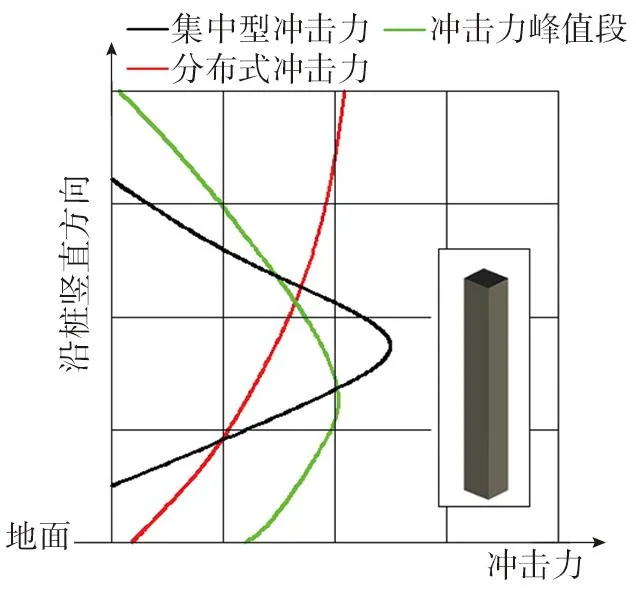
图3 不同时段碎屑流冲击力的分布形式Fig.3 Distribution pattern of impact force of debris flow in different stages
本文主要建立2种冲击形式下的消能计算模型,分别是考虑碎屑流呈连续性流体时的抛物线型冲击力作用下的消能桩消能计算模型,如图3中分布式冲击力所示;和考虑大颗粒滚石冲击作用下的消能计算模型,如图3中集中型冲击力所示。2.2.1节和2.2.2节主要介绍滑坡碎屑流冲击力的计算推导过程,为计算模型的建立提供依据。
2.2 动力作用计算模型
2.2.1 碎屑流速度计算
滑坡碎屑流与消能桩结构的动力计算模型是建立在滑坡碎屑流冲击力的计算基础上的,滑坡碎屑流向下运动时,将其视为连续流动,冲击力的大小主要由碎屑流的速度确定,本文根据碎屑流在垂向上的速度分布确定消能桩上冲击力的分布。在此基础上,将碎屑流简化为连续介质,引入碎屑流的垂向速度分布,推导碎屑流冲击力的垂向分布计算模型,并在该分布式冲击力作用下研究消能桩的动力计算模型。
碎屑流的运动速度由消能桩的布设位置确定。根据消能桩的布设位置计算滑坡碎屑流运动到消能桩处流过的路程D,由能量守恒定理推导得到碎屑流冲击消能桩时的平均速度计算式为
(1)
式中:ua为碎屑流冲击过程的平均流速(m/s);m为滑坡碎屑流的质量(kg);μ为等效摩擦系数。
碎屑流在运动过程中,会在底部出现一小段非流动层,且底面处的速度为0,在该段上速度直线增加,但是这段厚度一般较小,可忽略不计。WANG等[29]通过研究倾斜渠道中碎屑流的速度分布,认为碎屑流的速度在表面最大,底面处接近于0,从自由面向下,速度不断减小,这种说法在试验中被验证,并得到广泛应用。由于在实际工程中,滑坡碎屑流的粒径大小不一,且在堆积体中难以测量,因此本研究中的速度分布计算忽略了颗粒粒径的影响,只考虑碎屑流的厚度和表面流速,由此可推导出碎屑流的垂向速度分布式为
(2)
式中:y为竖直方向坐标;δ为碎屑流的厚度。垂向速度的计算参数通过调研很容易得到,底面处的速度等于0,接近自由面部分呈现均匀分布,与WANG等[29]试验中碎屑流的速度分布相符合。
2.2.2 碎屑流冲击力计算
将滑坡碎屑流简化为Bingham流体,从物源地在自重作用下发生运动,运动过程中存在粘性和剪切特性。在计算碎屑流的速度分布时,将其视为定常剪切流动,垂直坡面不产生速度分量。简化计算时,如图4所示将碎屑流简化为二维平面上的流动,碎屑流的密度为ρ,粘性系数为μ。坡体的倾角α由滑坡体的源位置与滑坡堆积位置的倾角确定;根据防护对象位置,消能结构的作用是消耗碎屑流的动能,将滑坡堆积位置提前一定距离。
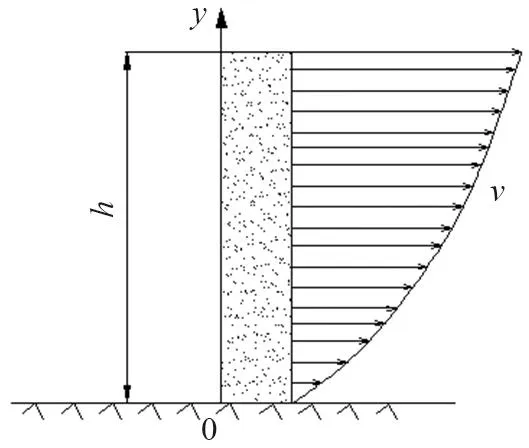
图4 运动速度垂向分布图Fig.4 Distribution of vertical velocity
滑坡碎屑流在某一位置的冲击力由碎屑流的速度和碎屑流的流动特性确定,HOLTZINGER等[30]根据试验分析得出滑坡碎屑流冲击力的经验计算式为
P=4.5ρv0.8(gh)0.6
(3)
式中:ρ为颗粒密度(kg/m3);v为颗粒流冲击速度(m/s);h为冲击力计算点距离坡面的垂直深度(m)。实验室的模型试验中,碎屑流的速度相对较小,往往不会大于10 m/s,使得上述计算模型在实际应用中具有局限性,对于速度较大的碎屑流,计算出的冲击力大小与实际情况相差较大。基于此,KWAN[31]根据水动力模型,总结出适用更广的计算式为
P=αρv2
(4)
式中:α为运动过程的动压系数。值得注意的是,当碎屑流的冲击速度大于10 m/s时,消能桩上的冲击力将大于500 kPa(α为2.5,ρ为2000 kg/m3时),对于实际滑坡碎屑流冲击力的计算中依然相对有效,因此应用式(4)计算某一位置处滑坡碎屑流的冲击力是可行的。
本文考虑滑坡碎屑流的垂向速度分布,推导了抛物线型冲击力分布的理论计算模型,根据碎屑流在不同运动位置的冲击力计算式(4)和碎屑流速度的分布式(2),得到作用于消能桩的冲击力计算模型为
(5)
碎屑流与消能桩的动力作用,由滑坡碎屑流对消能桩的冲击力决定。根据冲击力分布,考虑滑坡碎屑流与消能结构的相互作用、消能桩的抗弯反力做功,设计消能桩的消能计算模型。
2.2.3 碎屑流对消能桩的(主动)冲击与消能计算
本文主要研究消能桩对滑坡碎屑流的消能作用,滑坡碎屑流与消能桩相互作用过程中,由于冲击力呈非均匀分布,因此需要计算验证消能桩的稳定性和单根消能桩的消能量。主要存在2种能量耗散方式:一种是滑坡碎屑流冲击(主动)消能桩,消能桩的变形能耗散滑坡碎屑流的动能;另一种是消能桩的抗弯反力做功。
在计算之前,做如下假定:
1)假定消能桩所受横向载荷均匀分布,只沿竖直方向发生变化;
2)消能桩水平方向的位移与等效模型的悬臂梁的挠度相等;
3)将消能桩划分为N段,并用每段中点的挠度、荷载作为该段的平均挠度、荷载。
作用于悬臂段的冲击力荷载采用差分方法进行处理,如图5所示。对于任意冲击荷载P,将第i段的荷载作用等效为一个集中力,其值为

(6)
式中:B为消能桩宽度;Δy为选取任意微小段在竖直方向的高度;yi为第i段的位置。根据梁上的冲击力分布,由结构力学原理推导出梁上每一段的弯矩计算式,并且由悬臂梁的挠曲微分方程确定消能桩悬臂段上每一段的挠曲变形,计算滑坡碎屑流动能转化为消能桩变形能的大小。其中梁的挠曲微分方程[32]表示为
(7)
式中:E、I分别为消能桩的弹性模量(kN·m2)和截面的惯性矩(m4);ω为冲击力作用下消能桩的变形挠度(m);M(y)为梁截面的弯矩(kN·m)。
将悬臂梁划分为N段,计算时,将每一段的冲击力分布简化为直线型分布,并简化为三角形分布式荷载和均匀分布式荷载,如图5所示,建立以地面为起点的y轴。

图5 悬臂梁冲击力载荷分布图Fig.5 Distribution of impact force load of cantilever beam
划分的第i段中,根据碎屑流的冲击力分布式推导均布载荷作用下的弯矩计算表达式为
(8)
式中q1为均布荷载时的冲击力大小,联立梁的挠曲微分方程可积分得到第i段的挠曲方程为
(9)
式中C1,C2是任意常数,可通过边界条件(y=0,θ=0;y=0,ω=0)确定。例如第一段梁高度为h1,代入边界条件得到挠曲方程为
(10)
同理,计算三角形载荷作用下,梁的弯矩计算表达式为
(11)
式中q2为三角形荷载作用下的最大冲击力,联立求解,第i段悬臂梁在三角形载荷作用下的挠曲方程为
(12)
式中B1,B2为任意常数,由每段梁的边界条件确定。例如第一段梁的边界条件为y=0时,地面处的转角和挠度均为0,因此第一段梁在三角形载荷作用下的挠曲方程为
(13)
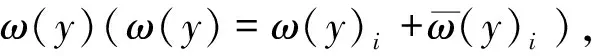
只要消能桩与碎屑流存在接触,则消能过程就一直持续。消能桩的抗弯反力(P′(y))与碎屑流的冲击力是一对相互作用力,根据滑坡碎屑流冲击力计算模型确定。消能桩的2个消能过程:一是滑坡碎屑流的冲击(主动)作用下,由消能桩的变形消耗的能量,由抗弯反力P′(y)和变形挠度ω(y)确定;二是碎屑流流动过程中,消能桩的抗弯反力(被动)作用的消能,由碎屑流对消能桩冲击力和二者之间的相对运动距离s来确定,由力学原理可确定单根消能桩的消能量计算公式为
(14)
式中:Q′为单根消能桩的消能量;s为消能桩抗弯反力的作用距离,可根据碎屑流在运动过程中的深度和运动宽度,结合前期调研估计滑坡体的总方量估算碎屑流在运动时的堆积长度,作为抗弯反力方向上的运动距离:s=V/bh(V为滑坡体的总体积,b为滑体流动的宽度,h为碎屑流的流动深度);ω(y)为消能桩的挠曲变形。根据上述计算过程可确定单根桩对滑坡碎屑流的消能量,为后续消能桩阵的设计提供依据。
2.2.4 大颗粒滚石对消能桩的(主动)冲击与消能计算
滑坡碎屑流的颗粒粒径分布范围广泛,小到几毫米,大到几米。值得注意的是,碎屑流中粒径较大的滚石往往运动速度更快,对消能桩形成单独的冲击作用,并且大颗粒滚石的冲击力集中,往往会直接造成消能桩的破坏。因此在考虑滑坡碎屑流的消能计算时,需要验算在大颗粒滚石的冲击作用下,消能桩的整体稳定性。本文将大块石的冲击力简化为一个作用在消能桩悬臂段上的集中力P,集中力作用下悬臂梁的变形与冲击力的关系可通过式(15)、式(16)计算:
(15)
式中:u为消能桩的挠曲变形(m);P为冲击力(N);h为大块石作用在消能桩悬臂段的高度(m);E、I分别为消能桩的弹性模量(kN·m2)和截面的惯性矩(m4)。
(16)
式中M(y)为消能桩上受冲击位置的弯矩大小,由式(15)、式(16)联立可得冲击力与消能桩变形的关系,验算消能桩的稳定性。若单根消能桩在冲击作用下被破坏,则需考虑采用多排消能桩的防护形式拦挡大颗粒滚石。
由功能定理计算大颗粒滚石的冲击动能,单根消能桩的消能量取为最大形变量,以将滚石动能减小到0为消能目标,计算消能桩的排数为
(17)
式中:n为设计最少消能桩的排数;m为大块石的质量;v为大块石的速度。式(17)可保证消能桩阵的稳定性,保证在大颗粒(块石)的冲击作用下,消能桩阵仍然发挥消能作用,计算得到消能桩的排数可作为消能桩阵的设计依据,即在保证消能桩阵具有持续的消能作用时至少需要布设n排消能桩。
2.3 消能量计算与消能桩设计
消能桩主要用以防护滑坡碎屑流对下游的基础设施和人们生产生活不被影响,因此在设计消能桩的实际参数之前,需要计算实际滑坡灾害的冲击动能,以及在保障人们生命安全和基础设施安全的前提下,消能桩需要提供的消能量。
滑坡碎屑流的运动距离是判定其运动速度,储存动能的基础,可根据能量守恒定理计算滑坡碎屑流的运动距离为
(18)
式中:M为滑坡碎屑流的总质量;Δh为滑动前后滑体堆积的高差;Δz为滑动后堆积体的重心高度;f为滑体运动过程中的等效摩擦系数;S为碎屑流的运动距离。式中滑体总质量,滑动前后高差以及碎屑流在运动过程中的等效摩擦系数均可由前期地质勘察得到,在实际工程中可根据地形地貌等实际情况选取。滑动后碎屑流的最终堆积高度,根据滑坡体本身的性质,由现场试验进行简单测量,滑坡体最终堆积下来,速度为0,由式(18)可计算出滑坡碎屑流的运动距离S。
消能桩的主要作用是减少滑坡碎屑流的动能,使得滑坡碎屑流的最终堆积位置停留在防护对象之前,假设碎屑流最终堆积的位置与需要防护的建筑物位置的距离为L,在该处堆积的滑体与最终堆积位置的高差为Δz1,则需要消能桩提供的消能量为
Q=Mgf·L-MgΔz1
(19)
由式(19)计算出消能桩阵需消耗的总消能量,联立式(14)可计算确定至少需要的消能桩数量m=Q/Q′,为消能桩的设计提供依据。
综上所述,可将滑坡碎屑流-消能桩结构动力计算模型的具体计算步骤表述为:第一步,对滑坡灾害点展开地质调查,确定滑坡、消能桩的参数,并计算消能桩阵需要承担的消能量,滑坡碎屑流的运动距离,防护对象位置,碎屑流粒径等;第二步,根据获取的参数,采用式(5)、式(9),式(12)计算滑坡碎屑流的冲击力及其分布;第三步,根据冲击力的分布和消能桩参数,采用式(14),式(19)计算单桩的消能量和总的消能量;第四步,计算碎屑流中大颗粒滚石的冲击动能,以及消能桩对大颗粒滚石的消能量;第五步,根据计算出的单桩消能量,大颗粒滚石的冲击动能,设计消能桩的数量和排数,计算流程如图6所示。消能桩的行距以形成连续拦截效应为主要目的,消能桩布设形成一个整体,发挥类似于拦挡坝的效益,排布形式如图1所示;消能桩的布设位置根据地形地貌确定。下面通过一个算例验证上述计算模型并据此提出具体的消能桩设计过程。
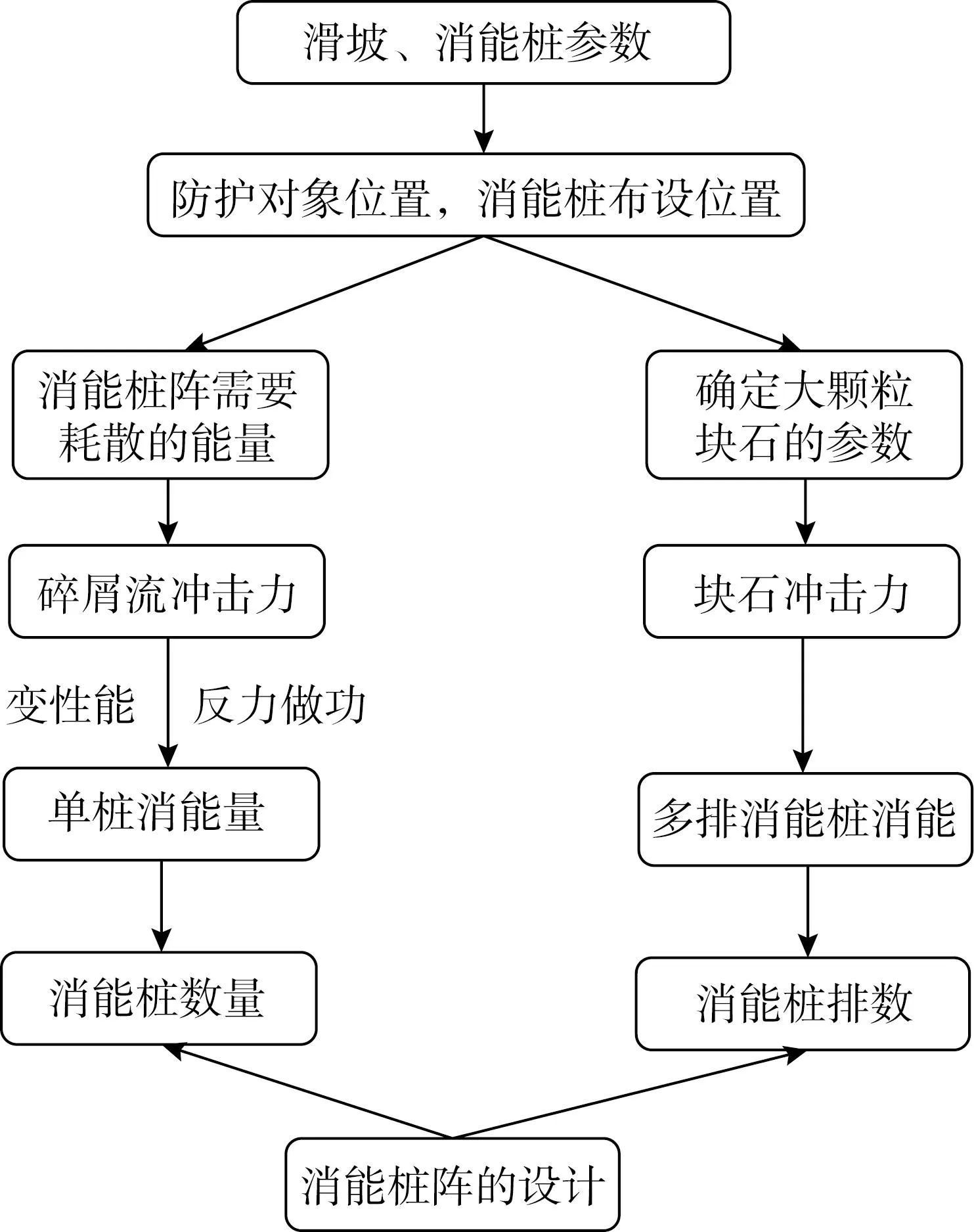
图6 计算流程图Fig.6 Flow chart of calculation
3 算例
3.1 背景资料
为验证本文理论计算的合理性,以西藏自治区某高速远程滑坡碎屑流灾害点为例,整体坡度26°,距离下游村庄约4.67 km,滑坡前后缘最大高差860 m,根据滑坡碎屑流水平运动距离和竖直高差估算等效坡度为11°,测算物源区滑体规模约为2.75×107~3.58×107m3,滑坡体源区出口段距离斜坡坡脚高差约为70 m,调查中测得碎屑流的重度约为28 kN/m3。距离该灾害点下游最近的防护对象是在滑坡体预测堆积体前缘300 m左右的村庄,该灾害点的工程地质剖面图如图7所示。计算灾害点的具体参数如表1所示。该灾害点对下游交通与基础设施造成极大的危害,亟需治理。
调查发现滑坡体主要含有黏土和碎石,碎石块的直径范围在5~300 cm内,因此设计消能桩时为考虑对大块石的拦截作用,消能桩悬臂段的高度设计为3 m。选用钢筋混凝土浇筑刚性消能桩,钢筋混凝土消能桩的标号根据工程实际选取,主要通过梁的挠曲方程复核后进行验算,桩的边长拟定为d0=1.0 m。根据混凝土施工规范确定消能桩的结构参数,初步选定标号为C20的混凝土修建消能桩阵,其中弹性模量为:2.55×104N/mm2,截面惯性矩I=bh3/12=0.0083 m4。土建工程中,对于梁结构,限制其挠跨比的范围为[ω/l]=1/500~1/250,l为梁的有效长度。将悬臂梁划分为10个小段,计算其挠曲变形和抗弯反力。
3.2 碎屑流-消能桩动力作用计算
第一步:参数获取。消能桩阵的位置设计在滑坡体源区出口段,距离斜坡坡脚高差约为70 m。由功能定理计算碎屑流从物源区运动至坡脚的平均速度为40 m/s,由消能桩阵流出的速度为32 m/s,本文的计算模型采用两者均值作为碎屑流速度分布计算的表面流速ua,等于36 m/s。
第二步:碎屑流冲击力(主动)的计算。根据混凝土施工规范已知,在土建工程中,梁的挠跨比的范围为[ω/l]=1/500~1/250,这里选取ω/l=1/250进行验算,梁长度为3 m,因此梁的最大允许挠度为12 mm。
由能量守恒定律计算滑坡碎屑流冲击消能桩时的平均速度为36 m/s,由式(20)可计算出碎屑流在垂直方向上的速度分布:
(20)
从而确定垂直方向上的冲击力(式(4)),其中α取3.0,h为3.0,ρ为滑坡碎屑流的密度,为2.8 g/cm3。将消能桩划分为10段,每段长度为0.3 m,根据式(4)计算每段消能桩所受的冲击力,如表2所示,冲击力分布如图8所示。
第三步:消能桩的稳定性与消能计算。将每段上冲击力的变化视为均匀变化,因此可以将冲击力分解为三角形载荷和均布载荷。对于三角载荷作用下,桩的变形采用式(12)进行计算,从地面向上以此计算,矩形均布载荷采用式(9)计算,从下向上叠加,最终得到各段结点处的变形挠度,如表2所示。经计算,消能桩的最大变形为6.045 mm,小于消能桩悬臂梁段的允许变形12 mm,失稳复核满足要求。
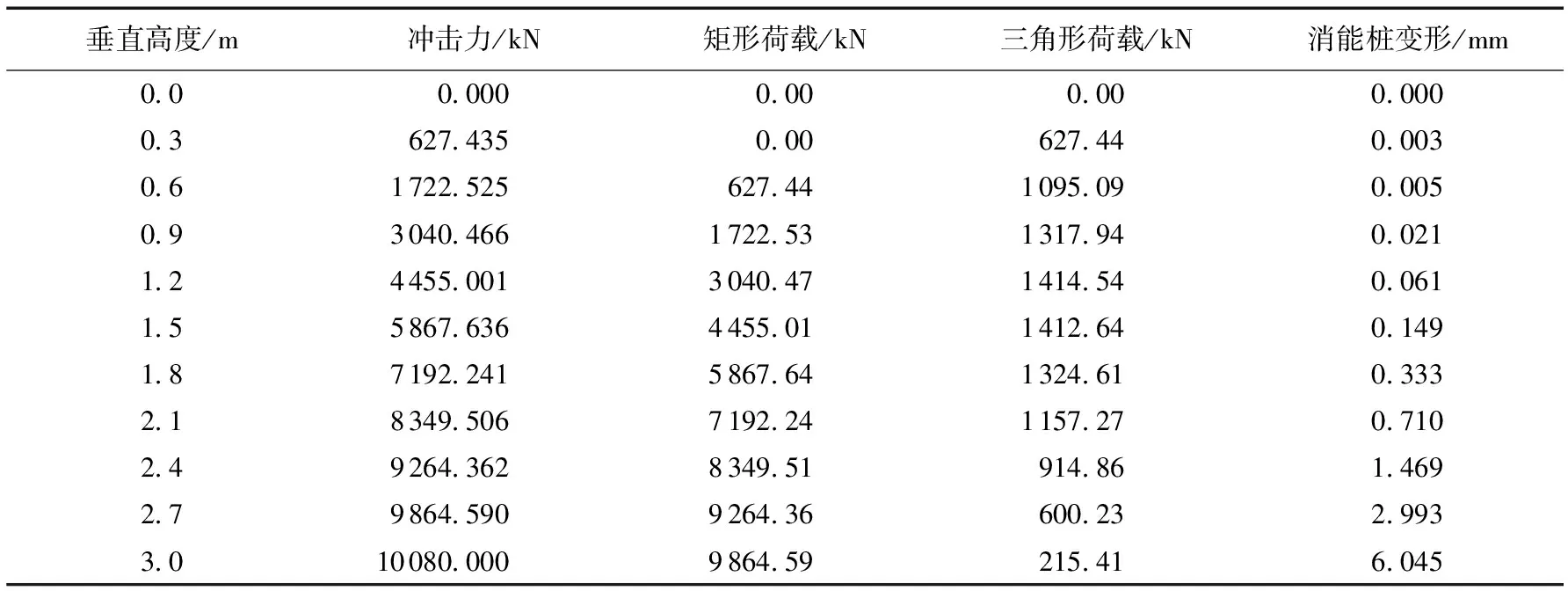
表2 碎屑流切向冲击力Table 2 Tangential impact force of debris flow
消能量计算:根据前期地质勘察得到滑坡碎屑流的物源与出口段之间的高差、总规模和等效摩擦系数,由能量守恒定律估算滑体的运动距离,计算最终的堆积区,冲击村庄后还继续向前运动约300 m,因此消能桩的效能效益取300 m,可保证村庄的安全,消能桩的总消能量按照式(19)计算:其中L=300 m,根据地形地质选取等效摩擦系数为0.08,根据计算出的滑坡碎屑流水平运动距离和竖直高差估算为11°,消能前后堆积体的高程相同,即Δz1为0,由式(19)计算出需要消能桩提供的总消能量为3.46×1012J。
消能桩设计:根据滑体规模、滑动路径的宽度以及运动过程中碎屑流的深度获得抗弯反力的作用距离s,结果为4428 m。根据式(14)计算单根消能桩的抗弯反力在整个冲击过程中做功和消能桩变形消能量之和为1.51×1011J。需要消能桩阵提供的总消能量为3.46×1012J,则至少需要布设的消能桩数量为:[3.46×1012/1.51×1011]+1=23根。
第四步:碎屑流大颗粒滚石的冲击与消能计算。前期调查显示,碎屑流中块石直径的范围为5~300 cm,选用最大块石直径300 cm验算消能桩的稳定性。
根据现场调查显示,滑坡碎屑流中最大块石的直径为3.0 m,其质量为M=4πρ/3(D/2)3=39564 kg,假设撞击过程中的冲击力大小恒定,则根据式(4)计算出冲击力的大小为 1.28×105kN,冲击力作用的位置在消能桩的悬臂段中间部分。在集中荷载作用下消能桩的挠曲变形按照式(15)计算,其中悬臂梁的长为1.5 m,运用积分计算在该冲击力作用下消能桩的消能量为6.36×106J。大块石的动能为E=mv2/2=2.56×107J,在保证消能桩阵整体稳定性的前提下,根据式(17)计算出至少需要消能桩的排数:25.6/6.36=4.025,即至少需设计4排消能桩,这里取4排。
第五步:消能桩阵设计。根据上述计算得出在冲击力作用下单根消能桩的最大耗能量,确定在防护下游村庄安全前提下所需要的消能桩数为23根,保证消能效益的前提下,消能桩的排数至少为4排,这里设计布置4排。为保证消能桩系统的稳定性,可选择增加1根消能桩,便于布设。碎屑流的运动具有流体的连续性,因此各消能桩的布置呈梅花型,每排的桩间距取1 m,每排布设6根消能桩,每排消能桩的间距根据地形条件设计为1 m。
上述计算中,考虑了消能桩的变形能和桩的抗弯反力做功来耗散滑坡碎屑流的动能,由下游村庄位置确定消能桩阵的作用是将滑坡碎屑流的堆积位置提前约300 m。同时,针对滑坡碎屑流中的大颗粒块石,计算中设计多排消能桩拦挡,将大颗粒块石的动能完全耗散的同时,也保证了消能桩阵的稳定。由此设计的消能桩阵,即可以满足防护作用的要求,也可以保证消能桩阵的稳定,表明上述计算方法的可行性。综上所述,本文提出的消能桩计算方法,应用到实际滑坡碎屑流灾害的消能桩设计是可行的,能够为滑坡碎屑流灾害的工程防护提供一定的设计建议。
4 结论
本文研究了滑坡被动防护中的一种消能桩的设计方法,考虑消能桩的2种消能形式,即桩的变形能和抗弯反力做功消能,以消能桩的变形理论为基础,假设地基是不发生变形的刚体,研究了消能桩挠曲变形和反力做功的理论计算方法;通过计算碎屑流冲击作用下消能桩的挠曲变形验证消能桩的稳定性,结合功能原理对消能桩的消能量和消能效益进行研究,得出以下结论:
1)根据水动力学模型,结合碎屑流的垂向速度分布推导了碎屑流冲击力分布计算模型,为探明滑坡碎屑流-消能桩结构动力作用提供理论依据。运动过程的冲击力根据功能原理计算得出的平均流速与实际情况存在一定的差异性,运动速度的计算模型后续会继续研究并补充。
2)计算中考虑2种消能方式,一种是消能桩的变形能,另一种是消能桩的反作用力做功。计算中假设冲击力在碎屑流与消能桩的接触过程中一直存在,计算出消能桩的消能量将大于其实际承担的消能量,在理论上是可行的。
3)提出了一种消能桩的设计方法:即根据地形、消能效应设计计算滑坡碎屑流防护所需的消能桩数量和排数,该计算模型在算例中得到验证。在基于功能原理、碎屑流速度、冲击力和悬臂梁的挠曲变形计算过程中,合理的假设和正确的理论模型是计算正确的关键。文中未考虑消能桩位置、排布的影响,忽略每排消能桩受力的差异和消能桩之间的土拱效应,后续会继续开展研究。
