车辆荷载作用下斜拉索参数振动分析

路一鸣,刘 敏

(1. 中国建筑上海设计研究院有限公司,上海 200333; 2. 哈尔滨工业大学 土木工程学院,黑龙江 哈尔滨 150090)

0 引言

随着中国建造的迅猛发展,众多大跨度桥梁应运而生。现代斜拉桥能够方便人们出行,复杂的结构体系也使其具有良好的结构性能。随着斜拉桥跨度增加,斜拉桥的结构刚度减小,斜拉索的长度和柔度增大,极易引起斜拉索的大幅值参数振动。对于斜拉索参数振动的理论研究,WARNITCHAI等[1]将斜拉索的垂度曲线简化为二次抛物线并施加索端位移激励,斜拉索的响应出现了二次和三次非线性耦合,证明拉索和整体结构之间存在1∶1和1∶2共振;LILIEN等[2]不考虑斜拉索垂度,将斜拉索简化为张紧弦,以实际案例为基础分析斜拉索发生参数振动的可能性,并指出超长斜拉索自振频率较低,极有可能发生参数激励;基于有限元模拟的方法,于岩磊等[3]建立斜拉网壳有限元模型,分析了结构中拉索发生参数振动的可能性以及影响因素,并对“拍”现象进行理论分析;李永乐等[4]建立斜拉桥和斜拉索的有限元模型,考虑车桥耦合的因素,对车辆荷载作用下斜拉索的参数振动进行分析。目前针对斜拉索的参数振动研究,以理论和实验分析为主,基于有限元模拟的参数振动研究较少,且索端施加的多为规律的荷载激励,索端施加随机外部荷载的情况研究较少。

本文针对车辆荷载作用下斜拉索的参数振动进行研究,对斜拉桥全桥模型和斜拉索的有限元模型进行动力特性分析。在斜拉桥全桥模型上施加车辆荷载,提取斜拉索索端位移响应施加于斜拉索模型,分析斜拉索参数振动受车辆荷载的影响情况。

1 工程概况及全桥有限元模型

该超大跨径斜拉桥为半漂浮体系斜拉桥,主航道长度为1088 m,闭口钢箱梁含风嘴宽度为41 m,中心线处梁高为4 m。索塔高度为300 m,塔柱呈倒Y型。斜拉索采用1770 MPa平行钢丝,最长拉索长度为577 m。该斜拉桥主跨结构布置如图1所示。

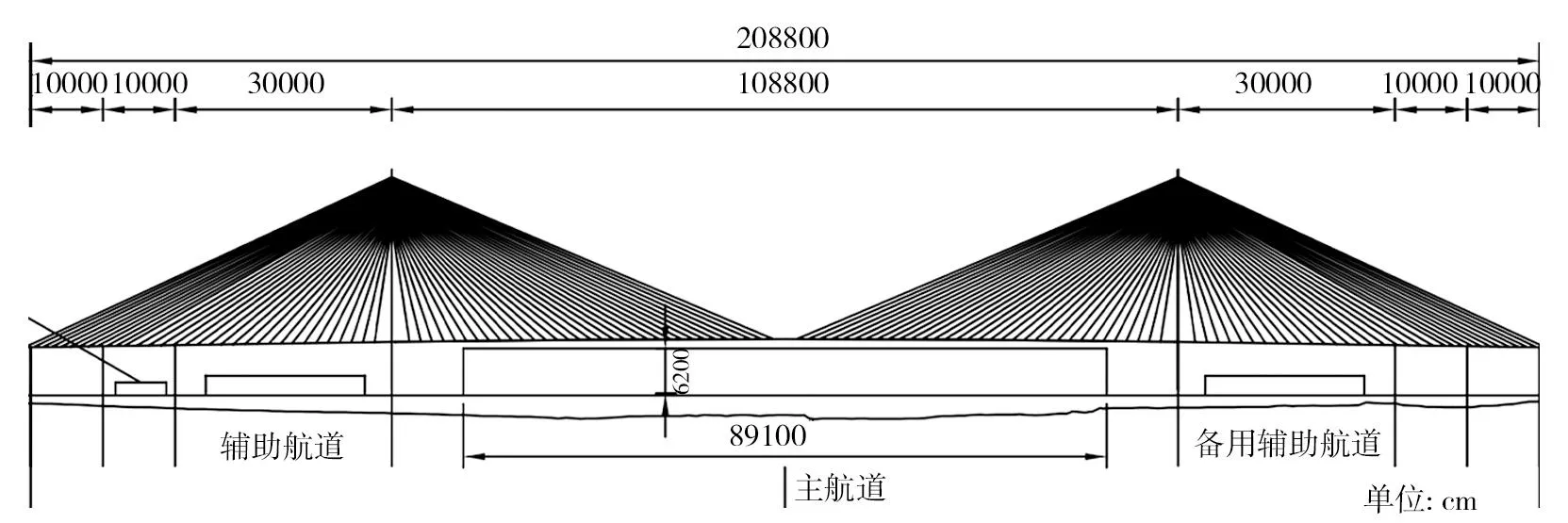
图1 斜拉桥主跨结构布置Fig.1 Structural arrangement of main span of cable-stayed bridge

基于某超大跨度斜拉桥的设计资料,采用空间杆系的建模方法建立全桥有限元模型,BEAM188单元用于定义主梁、主塔、桥墩以及刚性横梁,LINK10单元用于定义斜拉索,MASS21单元用于定义集中质量,并用弹簧单元COMBIN37模拟黏滞阻尼器,将阻尼器按照工程实际放置于斜拉桥的主塔和主梁之间,最后采用CP耦合命令准确模拟桥梁各结构构件之间的连接方式以及边界条件,全桥有限元模型如图2所示。

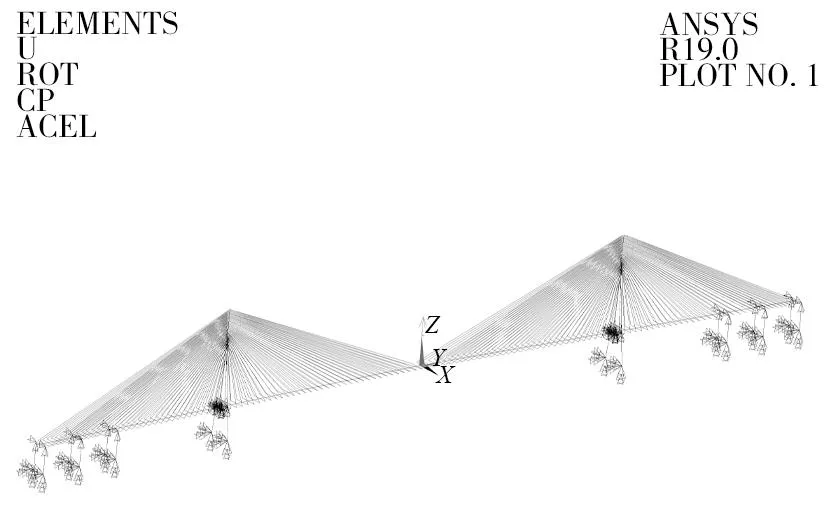
图2 全桥有限元模型Fig.2 Full-size finite element model of the bridge

斜拉索在超大跨度斜拉桥的荷载传递中起到了至关重要的作用,它作为桥塔和主梁之间的重要连接构件,使得桥塔和主梁在随机的外部荷载激励下能够均衡受力,所以斜拉索的受力和应变情况需要在有限元模型中进行准确模拟,本文采用初应变迭代法[5]进行斜拉索的索力调整[6]。列举了多条斜拉索调整索力之后的索力误差,如表1所示。

表1 索调后斜拉索的索力误差Table 1 Cable force error after several cable adjustment

2 全桥动力特性分析

模态分析[7]是研究结构动力特性的一种常用方法,文中采用分块兰索斯法对斜拉桥进行动力特性分析,得到全桥多阶频率及振型特征,根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》[8]给出的经验公式,计算得到斜拉桥一阶对称竖弯以及一阶对称扭转的频率值,与数值模拟结果相仿。斜拉桥主要模态频率及对应的模态振型如表2和图3所示。

表2 斜拉桥模态分析结果Table 2 Modal analysis results of cable-stayed bridge

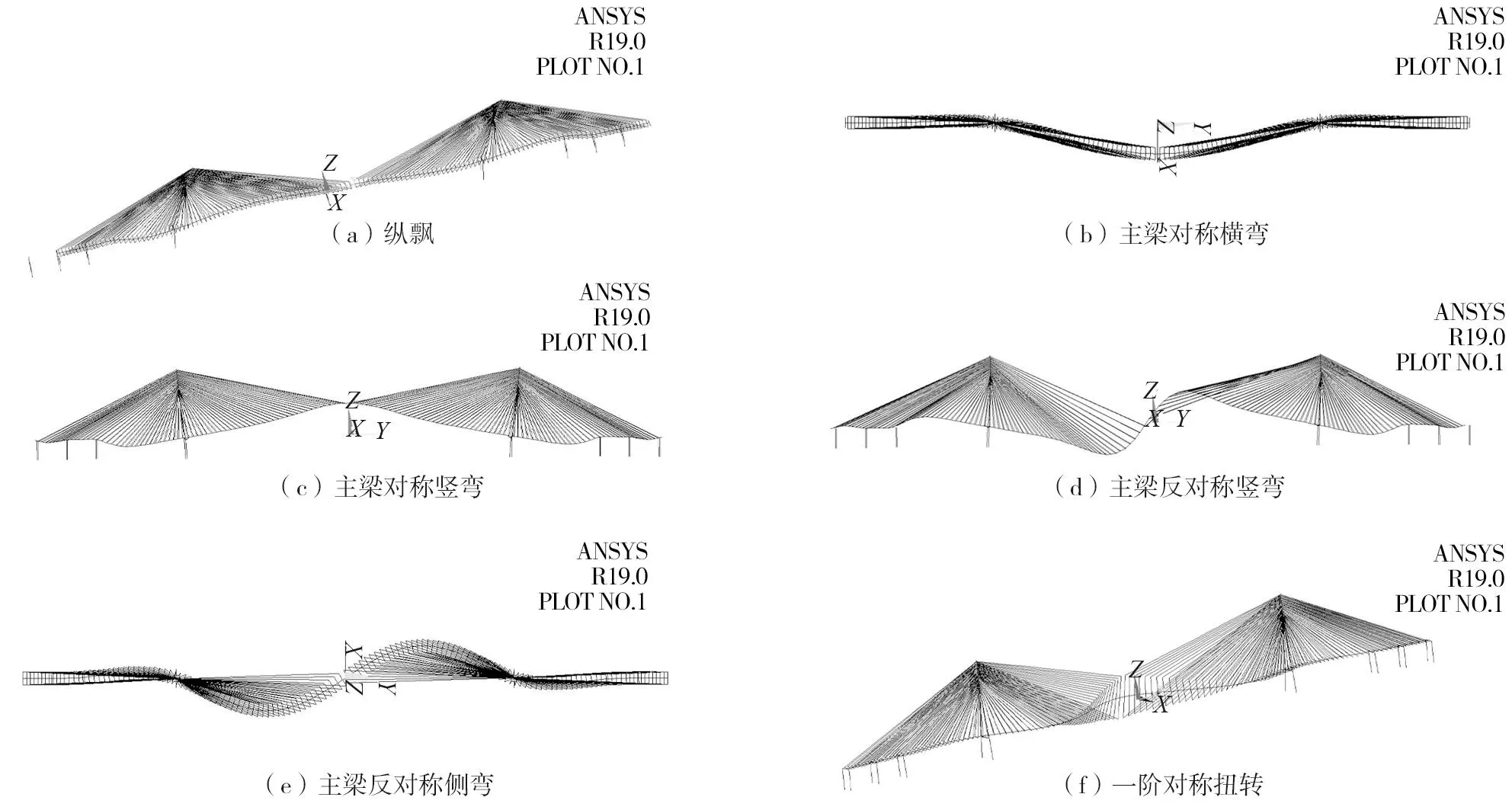
图3 主要模态阵型图Fig.3 Major mode shapes

3 斜拉索模型建立和模态分析

按照斜拉索所在位置分为江侧斜拉索Ji(i=1～34)和岸侧斜拉索Ai(i=1～34),从桥塔向两侧索编号逐渐增大。斜拉索J34是斜拉桥的最长拉索,以J34为研究对象建立斜拉索有限元模型。索J34长577 m,成桥恒载索力值(塔端)为6810kN,成桥恒载索力值(梁端)为6590kN,拉索面积为1.9597×10-2m2,无应力状态下的均布质量为102.03kg/m,弹性模量为1.95×1011Pa,本文采用赵海霞等[9]提出的等效弹性模量法的简化公式,得到了考虑垂度效应之后J34的等效弹性模量1.8738×1011Pa。采用索单元LINK10建立斜拉索模型[10],拉索两端采用固定约束。A点表示斜拉索与桥塔的连接点,B点表示斜拉索与桥面主梁的连接点,O点表示斜拉索的中点,节点坐标系用小写字母x、y、z表示,斜拉索的位移响应用大写字母X、Y、Z表示。x向表示横桥向,y向表示顺桥向,z向表示竖向。X向表示斜拉索的面外位移,Y向表示沿着索轴线产生的面内位移,Z向表示垂直于索轴线产生的面内位移。斜拉索模型如图4所示。

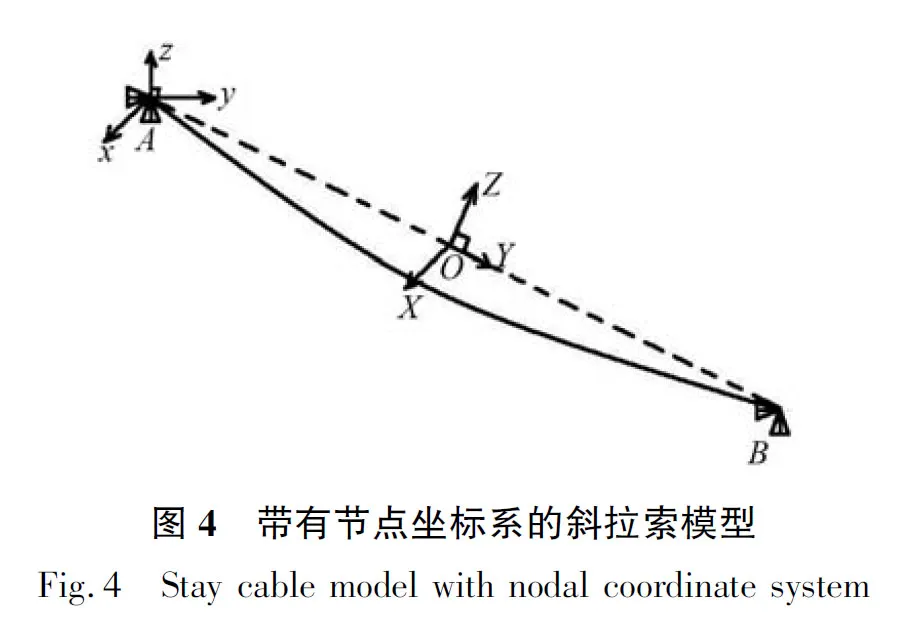
JTG/T 3360-01—2018《公路桥梁抗风设计规范》[8]给出了斜拉索的频率估算公式,与有限元模态分析得到的斜拉索各阶频率相近,验证斜拉索模型及模态分析的正确性,模态分析结果和斜拉索对应的模态振型如表3和图5所示。

表3 斜拉索有限元模型模态分析Table 3 Modal analysis of the finite element model of the stay cable振型阶数有限元频率值/Hz理论计算频率值/Hz模态振型情况一阶0.2250.225面外一阶对称二阶0.2530.226面内一阶对称三阶0.4590.450面内二阶反对称四阶0.5000.450面外二阶反对称五阶0.6890.675面外三阶对称六阶0.6900.675面内三阶对称

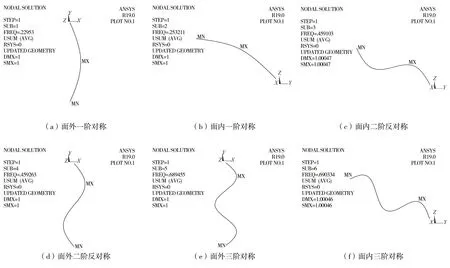
图5 斜拉索J34各阶模态振型曲线Fig.5 Mode shape curves of each mode of the stay cable J34

4 简谐激励下斜拉索参数振动

在斜拉索J34两端施加频率为0.2532 Hz(索J34的一阶自振频率)的规律正弦激励,采用完全法进行瞬态分析[11],正弦激励幅值A=0.25 m,时间间隔Δt=0.1 s,计算步数n=5000,忽略阻尼的影响。如图6所示,当斜拉索所受外部激励频率与斜拉索基频呈1∶1的关系时,斜拉索会产生非常大的位移响应,斜拉索中点面内竖向位移响应高达所施加正弦激励幅值的40倍,此时激起了斜拉索的一阶主共振,发生“拍振”。由图6(b)可知,幅值达到最大时对应的频率值为0.254 Hz,与索一阶自振频率相近。拍振的发生是由于在索端施加的正弦激励频率与斜拉索基频相近, 但由于斜拉索自身的振动并不是单一的简谐波形振动,且斜拉索在阻尼及外部条件的作用下振动呈衰减趋势,所以斜拉索主共振的激励幅值随时间延长也会相应减小。由此分析得出,当斜拉索所受外部频率激励很小,但是外部激励频率与斜拉索基频呈1∶1关系时,产生的位移响应不可忽视。

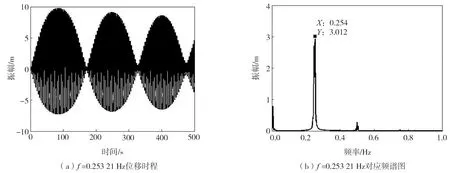
图6 正弦激励下斜拉索中点Z方向的位移幅值时程Fig.6 Time history of displacement amplitude in the Z direction at the midpoint of the stay cable under sine excitation

5 施加车辆荷载后斜拉索的参数振动

5.1 基于车桥耦合建立振动方程

车桥耦合振动[12],指的是车辆在桥面上行驶时,二者产生的位移响应会相互影响,是车辆和桥梁相互性的一个力学作用。车辆对桥梁有重力作用、阻尼力作用、惯性力作用,这些力除了重力,阻尼力和惯性力都是会发生改变的。采用Newmark-β法建立车桥耦合系统的运动方程[13],桥梁和车辆的振动方程见式(1)～式(2):

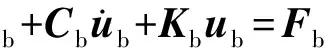
(1)

(2)

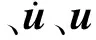
通过建立车桥之间的位移协调和受力平衡条件,得到车桥耦合系统的运动方程为

(3)

式中 :Mbv(t)为车桥耦合系统的广义质量矩阵;Cbv(t)为系统的阻尼矩阵;Kbv(t)为系统的刚度矩阵;δ分别为车辆的各自由度以及桥梁广义模态坐标组成的列向量;Fbv(t)为系统的广义荷载列向量。

5.2 考虑桥面不平顺因素

在实际工程中,桥面不平顺通常是由于外部环境、温度、施工和交通重复荷载等不可避免的因素导致的。根据不同的区别要素可以分为动态和静态不平顺、水平和高低不平顺。动态不平顺和静态不平顺的区别要素在于桥面上有无荷载,水平不平顺和高低不平顺的区别要素在于桥面的不平顺方向。

本文应用美国六级谱模拟桥面的高低不平顺,表达式为

(4)

式中:SV(Ω)为高低不平顺桥面谱密度[cm2/(rad/m)];k为安全系数,取0.25;AV为粗糙度常数(cm2·rad/m),美国六级谱取0.0339;ΩC为截断频率(rad/m),美国六级谱为0.8245;Ω为桥面高低不平顺谱的空间频率(rad/m)。

高低不平顺样本与功率谱密度曲线如图7所示。

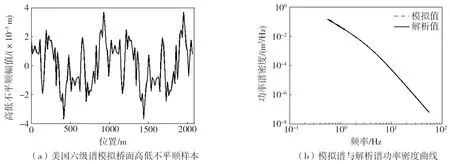
图7 美国六级谱模拟桥面高低不平顺样本与功率谱密度曲线Fig.7 Sample of bridge deck irregularity simulated by American six-level spectrum and power spectral density curves

5.3 车辆荷载作用下全桥振动分析

建立车辆模型存在多种模型简化方法[14]:移动荷载模型、移动集中质量模型、移动均布质量作用模型、移动质量加弹簧的作用模型。前3种简化方法单纯地考虑了车辆的荷载或者质量,而现在车辆普遍安装有弹簧减振装置,所以本文采用车轮加弹簧加质量的方法模拟车辆。

在ANSYS中实现车桥耦合主要有3种方法:位移耦合法、生死单元法和位移接触法。本文采用位移耦合法实现车桥耦合,采用CP命令模拟车辆在桥面上的行进过程。车辆模型的上下质量用质量单元MASS21模拟,上下质量之间的弹簧单元用COMBIN14模拟。利用ANSYS完全法进行瞬态分析时,采用Rayleigh阻尼假定,表达式如下:

C=αM+βK

(5)

式中:α、β分别为质量阻尼系数、刚度阻尼系数;M、K分别为结构质量矩阵、结构刚度矩阵。

质量阻尼系数和刚度阻尼系数不是已知的,通过正交性原理,任一阶模态阻尼比ξi、自振频率为ωi满足以下公式:

(6)

(7)

JTG B01—2014《公路工程技术标准》[15]规定高速公路的设计速度不宜低于100 km/h,受地形、地质等条件限制时,可以选用80 km/h。根据不同的天气情况,超大跨度斜拉桥经常会采取不同的限速标准,最高时速不得超过设计速度100 km/h。为保证本文分析结果的可靠性,取3组时速进行分析,分别取80、100、120 km/h的行进速度,得到3组索J34梁端节点的位移时程曲线以及频谱图,如图8～图10所示。

图8 速度为80 km/h时最长索J34索端位移时程及频谱曲线Fig.8 Displacement time history and spectrum curve of cable end of the longest cable J34 at the speed of 80 km/h

图9 速度为100 km/h时最长索J34索端位移时程及频谱曲线Fig.9 Displacement time history and spectrum curve of cable end of the longest cable J34 at the speed of 100 km/h

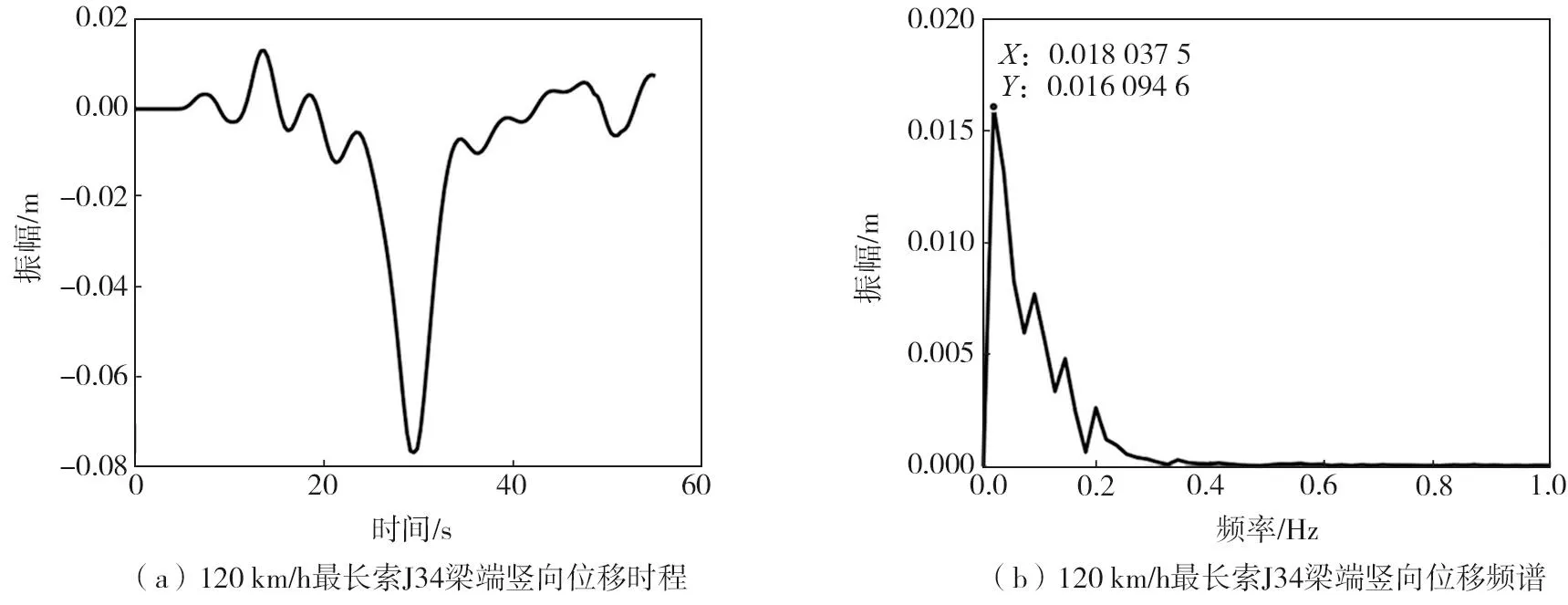
图10 速度为120 km/h时最长索J34索端位移时程及频谱曲线Fig.10 Displacement time history and spectrum curve of cable end of the longest cable J34 at the speed of 120 km/h

图11 车辆时速与索端频率的关系曲线Fig.11 Curve of the relationship between vehicle speed and cable end frequency

分析图8～图10的位移时程曲线可知,随着车辆行进速度的增加,斜拉索梁端节点发生最大位移响应的时间点随之提前,在不同车速情况下,位移时程曲线的形状是相同的,产生的最大竖向位移没有太大变化,表明车辆的行驶速度对斜拉索梁端节点位移响应影响不大。分析3条频谱曲线可得,随着车辆行进速度的增加,索端位移响应的主要频率成分增大,但是主要频率仍远小于斜拉索的一阶频率,所以当桥面上的车辆按照限速要求正常行驶时,斜拉索不会发生主共振或者参数共振。如图11所示,斜拉索索端位移响应频率与车辆时速呈线性增长的关系,所以若车辆速度超过该桥限定时速,斜拉索索端位移激励频率将进一步接近斜拉索的一阶固有频率,这时斜拉索便会产生巨大的位移响应,这也是桥梁上限制最高时速的原因之一。

6 结论

本文利用有限元软件ANSYS对某超大跨度斜拉桥及其拉索进行有限元分析,将有限元分析结果对比先前研究数据以及理论计算值,得到正确的斜拉桥和斜拉索有限元模型,验证了当在斜拉索端部施加规律的正弦激励且激励频率为斜拉索一阶固有频率时,斜拉索发生一阶主共振。

考虑车桥耦合以及桥面不平顺因素,采用完全法进行瞬态分析,用位移耦合法实现车桥耦合,建立上质量-弹簧-下质量的车辆模型,在该超大跨度斜拉桥的限制时速范围内,分析车辆在多组行驶速度下,斜拉索是否会发生主共振或者参数共振。分析得出,虽然斜拉索索端频率与车辆时速呈线性增长的关系,但是若车辆在桥梁所规定的时速范围内行驶,斜拉索索端位移响应的主要频率成分远小于斜拉索的一阶固有频率,不会激起斜拉索的共振。