空间异形拱桥振动台试验设计

2024-03-13刘芃汐张广达王利辉贾振雷

地震工程与工程振动 2024年1期

韩强,刘芃汐,惠斌,张广达,许坤,王利辉,贾振雷

(1. 北京工业大学桥梁工程安全与韧性全国重点实验室,北京 100124; 2. 北京市市政工程设计研究总院有限公司,北京 100082)

0 引言

异形拱桥由于造型优美、曲线圆润等特点,在城市景观桥梁中得到较为广泛应用。异形拱桥由于结构非对称性,在地震作用下具有较强的空间效应[1],特别是空间地震动与空间异构耦合作用下,结构和主要构件处于复杂的受力状态,各结构参数对异形拱桥作用机理尚不明确。尽管国内外已有一些涉及异形拱桥的抗震分析成果[2-7],但对于新型异形拱桥结构体系,仍需开展针对性的地震响应分析与模型试验验证工作。

桥梁振动台试验是研究桥梁在地震作用下动力特性和响应的主要手段[8-9],合理的模型缩尺设计是事关振动台试验是否成功的关键。郭葳等[10]以某大跨度斜拉桥为研究对象,设计制作了1∶35的全桥振动台试验模型,对比了桥梁纵向无约束体系与设置纵向黏滞阻尼器的减震体系的地震响应。谢文等[11]对一座1400 m的大跨斜拉桥进行了相似比为1∶70的振动台模型试验,在桥塔及主梁上安装配重箱以辅助配重,研究了多点激励对大跨斜拉桥地震响应的影响规律。王蕾[12]在量纲相似理论的基础上设计了几何相似比为1∶40的大尺寸曲线桥梁缩尺模型,采用铅板均匀布置在桥面和桥墩的附加配重方式,通过九子振动台阵系统开展了多点地震动激励作用下的动力响应分析。李勇[13]对一座三跨飞燕式钢管混凝土拱桥1∶16模型进行了振动台试验,通过吊挂配重方式完成了对多维地震动下的桥梁结构的动力响应分析。

基于以上研究表明,在已开展的桥梁振动台试验中,一般多为结构相对规则的桥梁,而对于结构形式复杂的异形拱桥振动台试验研究还不多见,从而造成在模型设计与制作上,如何保持与原桥动力特性相似等问题带来多方面的困难。鉴于此,本文针对一座主跨跨径为164.5 m的空间Y形拱桥按照1∶20的几何相似比进行缩尺模型设计,并通过ABAQUS软件建立有限元模型,对比原桥模型与缩尺桥模型的动力特性和响应,验证此类异形拱桥动力缩尺模型的合理性,为空间异形拱桥的抗震设计和类似桥梁振动台设计提供参考。

1 原桥结构与试验条件

1.1 工程概况

原桥主桥部分为“Y”字抱翅拱梁组合体系桥,全长256 m,桥跨布置为35 m+164.5 m+56.5 m,主桥段全宽为49.5 m。主桥采用抱翅型拱梁组合体系,由“Y”字空间异形主拱拱圈、拱圈内与主梁连接的斜吊杆和主梁三大主体结构组合而成。上部结构为南北两幅分离式钢箱式主梁,梁高为2.5 m,主梁半幅为整体钢箱,半幅之间用横梁连接,12对斜向布置吊杆锚固在异形拱和主梁边缘,桥面板采用正交异性钢桥面板。拱肋立面为椭圆线,断面采用矩形钢箱截面,高度沿拱轴线形逐渐变化,拱肋的一端在中央隔离带处与主梁横梁连接,下接中墩支座;另一端呈倒“Y”形分布于主梁两侧,通过横梁与主梁连接,双拱段设置横向连接,如图1所示。该空间异形拱桥位于设防烈度为8度,因此,超出现有桥梁抗震规范[14-15]规定的适用范围,需开展桥梁抗震专项分析,进行振动台试验研究。

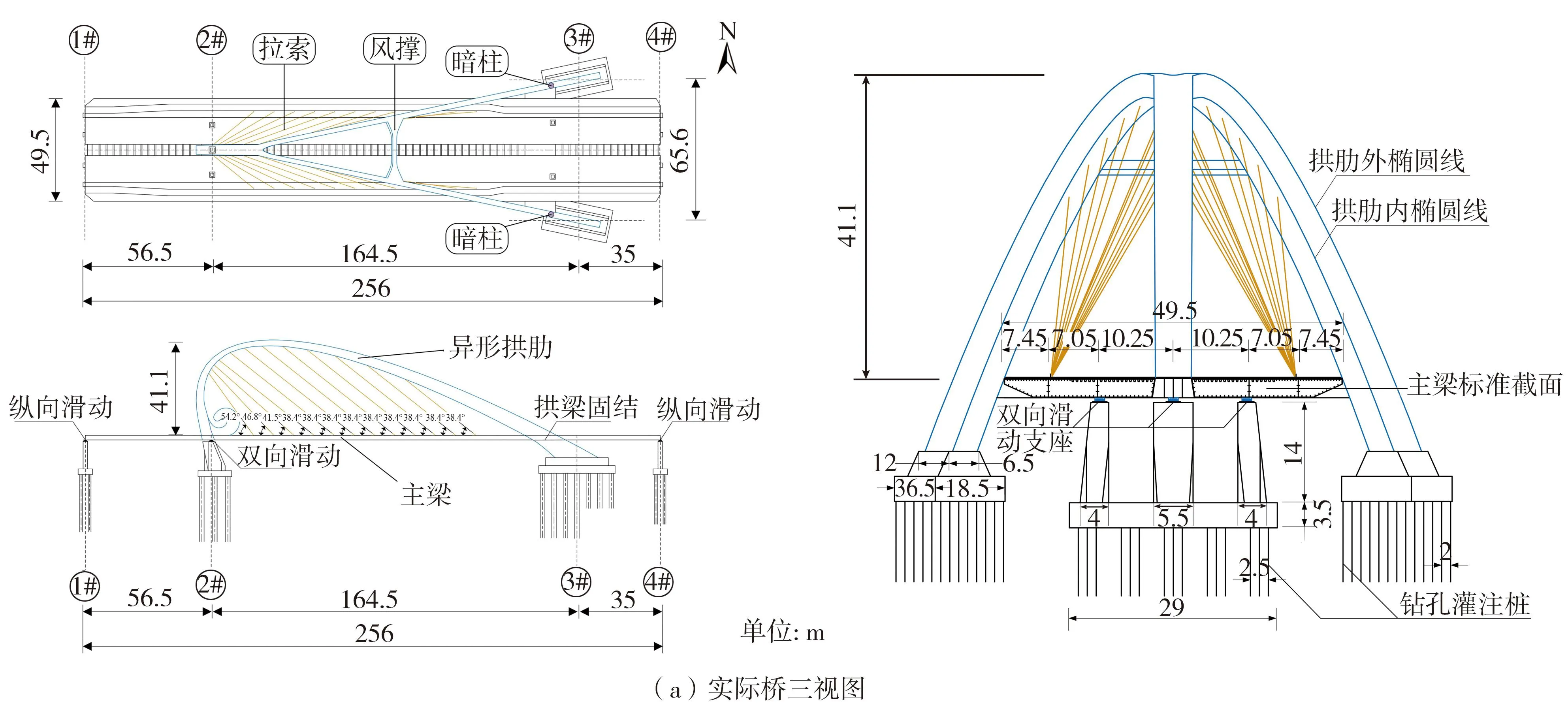
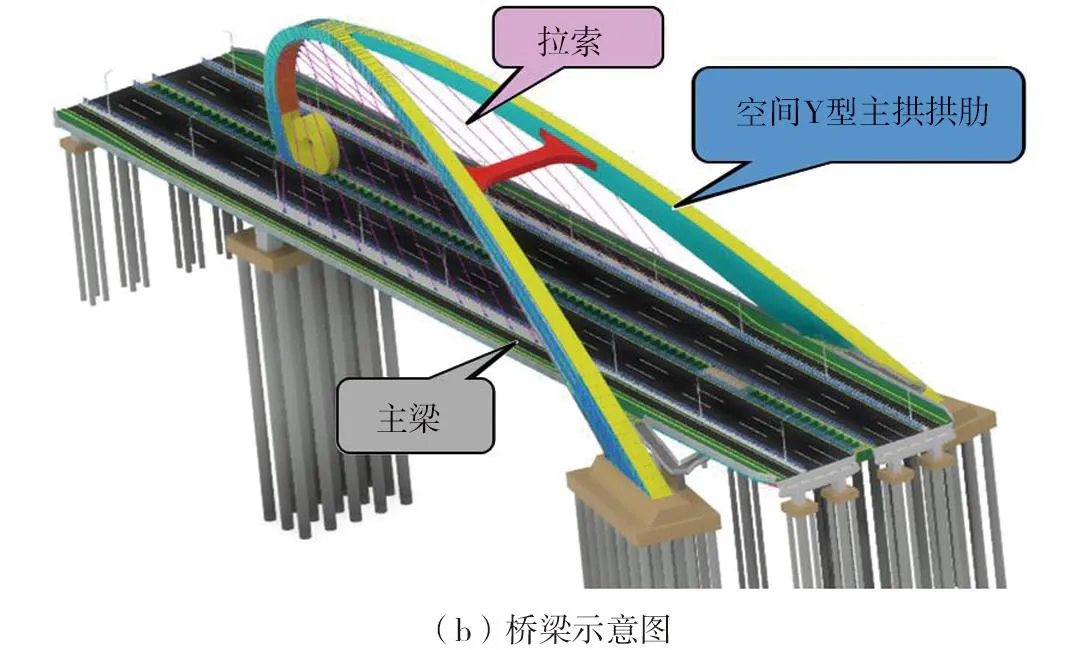
图1 异形拱桥结构图Fig.1 Structure of the special irregular arch bridge

1.2 试验条件

该空间异形拱桥振动台试验设计依托北京工业大学桥梁工程安全与韧性全国重点实验室的九子系统振动台阵[16]开展,其技术指标为:单台台面尺寸为1 m×1 m,振动方向为水平双向加竖向,最大速度为60 cm/s,单台最大荷载为5 t,满载最大加速度为水平1.5g、竖向1.0g,频率范围为0.4～50 Hz。此振动台阵系统由9个单台组成,每个单台可以布置在不同位置形成多种组合形式,为缩尺模型试验提供了较大的设计空间。

2 振动台模型设计

2.1 动力模型相似关系设计

要使缩尺模型与原结构模型满足动力学上的相似关系,即需要满足缩尺模型与原结构模型的几何相似关系、物理相似关系、运动相似关系与外部荷载相似关系[17]以及边界条件的相似关系。然而由于原桥结构复杂,各物理参数相互制约,在实际设计中,通常先确定几个基本量纲相似比,进而通过量纲分析法推导出剩余的物理量纲的相似比[18]。本试验目的是研究异形拱桥在地震动下的动力性能,因此设计模型时主要着手于缩尺模型与原桥模型的动力特性和响应相似,基于此目标,将长度、弹性模量和密度设定为基本量纲。在本模型设计时,定义物理量n的相似比Sn为缩尺模型物理量nm与原型物理量np的比值,表达式为

(1)

1)长度相似比SL的确定

确定长度相似比SL时,需要考虑以下两点:①动力缩尺模型尺寸不得超过振动台场地限制;②桥墩以及边跨支撑布置的各个振动台互不影响。结合振动台试验场地参数,缩尺模型与原结构模型的几何相似关系取1∶20,即缩尺模型长度为12.8 m,高度为3.1 m。

2)弹性模量相似比SE的确定

弹性模量的相似比SE根据动力缩尺模型选用的材料确定。原桥结构拱肋、主梁及横梁均采用Q420钢材,为使缩尺模型最大限度表示原桥模型的动力特性与结构响应,模型桥拱肋、主梁及横梁采用与原桥相同的Q420钢材,即弹性模量相似关系取为1。

3)密度相似比Sρ的确定

根据量纲相似法得

(2)

式中:SE为弹性模量相似比;SL为长度相似比;Sa为加速度相似比;Sρ为密度相似比。

根据现已确定的弹性模量相似比和长度相似比,若模型满足重力相似定律即

Sa=Sg=1

(3)

则密度相似比Sρ远大于1,那么结合式(2)换算理想的模型质量mm为

(4)

而使用相同材料的模型桥,其实际密度相似比为1,故模型桥实际质量为

(5)

对比式(4)与式(5),显然在缩尺模型选择的材料与原型结构相同的情况下,需要补足人工质量来满足模型质量的统一。附加人工质量需满足式(6):

(6)

式(6)需满足的前提为原型结构与模型结构采用相同的材料,即弹性模量相似比与实际密度相似比均为1,故在振动台试验中不同材料的选取对附加人工质量的计算完全不同。由于按式(6)计算的附加人工质量远超出本试验振动台的承载能力限制,故本试验无法采用全配重设计,即不能满足重力相似定律式(6)的要求。在既有振动台试验中往往采用弹性-重力相似律或弹性相似律,前者通过设置部分附加质量以满足加速度以及密度的相似关系,通过增大加速度来补足缺失部分质量的动力效应;后者则完全不设置附加质量,忽略模型的部分质量以及惯性力。结合本试验目的,为减小试验误差,本试验采用欠质量人工质量相似模型,即通过加速度来补足部分质量的缺失。由于忽略部分质量,那么密度的相似关系不能通过式(2)与式(3)得出,同理,加速度相似比也需重新计算。故本文提出,对于按弹性-重力相似律设计的采用相同材料的缩尺模型的密度相似比与加速度相似比为

(7)

(8)

式中x为实际附加人工质量与理想完全相似附加人工质量之比。

由原结构有限元模型在自重及二期荷载的荷载组合下计算出的基底反力并结合振动台最大承载能力可以得到动力缩尺模型的最大质量为19.95 t。为尽量真实的反映结构的动力特性与结构响应,且满足试验振动台的最大加速度限制,应尽量将动力缩尺模型质量取最大值。

通过长度、弹性模量和密度这3个基本量纲的相似关系,并结合量纲分析法可以求出剩余的量纲相似关系如表1所示。

表1 相似关系系数Table 1 Similarity relation parameters

2.2 动力模型尺寸设计

1)拱肋及风撑截面尺寸设计

原桥结构拱肋截面为矩形钢箱截面。由于原桥模型在低阶模态中均有拱肋参与,故模型设计时尽量保证拱肋外形与原桥相似,即截面形状保持不变,同时考虑材料特性与焊接难度,确定模型桥拱肋钢板厚度为8 mm。在有限元动力特性分析时,拱肋主要出现双向弯曲及扭转振型,而结构扭转模态的振动周期与截面积无关,弯曲模态的振动周期只和截面惯性半径有关[19],故换算截面特性时以截面X轴的惯性矩Ix、Y轴的惯性矩Iy以及截面扭转惯性矩J相似作为目标,且截面形状保持原有拱肋的箱型截面,从而确定模型桥拱肋截面的尺寸,拱肋截面对比如图2所示。拱肋和风撑关键截面缩尺前后截面特性如表2所示。

图2 拱肋示意图Fig.2 Schematic diagram of arch rib

表2 拱肋及风撑截面特性Table 2 Section characteristics of arch rib and wind brace

2)主梁及横梁截面尺寸设计

原桥结构为分离式双主梁设计,南、北两主梁之间采用横隔板连接,模型桥拱肋示意图如图3所示。若主梁采取与拱肋相同的设计方法,缩尺模型的主梁与横梁壁厚只有3 mm,这造成现实选材困难且加工工艺难以实现等问题。故在设计时采用更为灵活的处理办法:只保证主梁纵向长度的几何相似,忽略主梁截面形状的几何相似,在满足弹性恢复力相似的条件下,根据钢材材料特性及加工难度,模型主梁与横梁选择厚度为8 mm的Q420钢板为主要材料,截面形式采用箱型截面。同时为保证在动力特性分析中与原有模型的频率满足相似关系,需保持双主梁整体截面X轴的惯性矩Ix,Y轴的惯性矩Iy与截面扭转惯性矩J相似。前、后横梁作为连接主梁与拱肋的关键构件,为使整桥刚度矩阵与原型桥保持统一且构成完整的拱梁组合体系,同样以截面X轴的惯性矩Ix、Y轴的惯性矩Iy以及截面扭转惯性矩J相似作为截面换算的目标。主梁与横梁关键截面缩尺前后截面特性如表3所示。

图3 模型桥拱肋配重示意图Fig.3 Schematic diagram of the model bridge arch rib counterweight

表3 主梁及横梁截面特性Table 3 Section characteristics of main beam and beams

3)其他截面设计

原桥吊杆利用冷铸与挤压复合锚固技术,采用Ryb为1860 MPa,E为1.95×105MPa级的钢绞线成品索,为更好的还原吊杆在整体结构中的受力情况,模型桥吊杆采用相同材料并以抗拉刚度为目标进行相似设计,即截面面积满足几何相似关系,换算前后索力如表4所示。原桥的墩柱为钢筋混凝土材料,考虑模型按几何相似关系缩尺后由于混凝土截面面积过小,若采用与原桥截面材料相同的材料,其钢筋保护层厚度无法保证,施工工艺复杂,故采用换算Q420钢材。为简化分析,将EI与EA作为复合物理量进行缩尺设计,反映换算前后的截面刚度相似,即墩柱截面X轴的抗弯刚度EIx,Y轴的抗弯刚度EIy与抗压刚度EA相似,截面形式采用厚度为8 mm的箱型截面。

表4 索力对比表Table 4 Comparison of cable forces kN

2.3 动力模型配重设计

动力模型质量是计算缩尺结构动力特性和响应正确与否的关键参数,由于动力模型材料采用与原桥相同的Q420钢材,若满足相似关系中密度的相似关系,则需通过附加质量配重的补偿方式来实现[20-21]。本试验缩尺模型自重及附加人工质量总计19.95 t,其中附加人工质量由经过换算后的结构自重密度补偿质量与桥梁二期荷载组成。

对于此种大跨空间异形结构拱肋在附加人工质量块时,需要考虑三个方面:①附加的人工质量块不得影响原有拱轴线的线形;②附加人工质量块后不能大幅度影响所在截面的截面特性;③附加人工质量块在地震动下应与拱肋有较好的整体性。

本设计将通过节点附加人工质量块的方式实现质量补偿。为保证拱肋每一块拼接板之间的焊接质量,将附加人工质量的节点设计在每一块钢板的中央。其装配形式为:在拱肋的每一节段的左右边板中央钻有M30的螺栓孔,将M30的螺杆穿过拱肋并在两端留出等长部分,利用M30螺母预紧夹持在拱肋两端固定螺杆,将附加人工质量块中间与两端各钻有M30与M10的螺栓孔,并在M30螺孔内设置螺纹,把一定数量的质量块对称加在螺杆两端,最终在螺杆两末端利用M30螺母夹持固定,四周利用M10螺母夹持。拱肋节点附加质量节段如图3所示。

为保证附加人工质量块与拱肋在地震动下具有较好的一致性,螺杆直径与附加人工质量块的尺寸需通过ABAQUS计算验证,暂定人工质量块的尺寸为20 mm×100 mm×200 mm与20 mm×100 mm×300 mm,螺杆直径为30 mm。建模时以最大附加质量的节点所在的拱肋节段为基础,建立螺杆与附加人工质量块的实体单元模型,其中螺杆与质量块之间采用绑定约束,螺杆一端固定。将模型进行动力特性分析,选取单方向振型并计算阻尼系数。原桥结构的地震动时程曲线按时间相似关系与加速度相似关系换算为模型桥换算地震动时程曲线。在螺杆固定端释放X方向约束并输入换算后的地震动,通过对此模型进行动力时程分析,其应力峰值未超过420 MPa,螺杆两端相对位移最大值未超过0.1 mm,螺杆两端相对位移如图4所示。故设计尺寸满足配重结构与拱肋部分具有良好的一体性的条件。

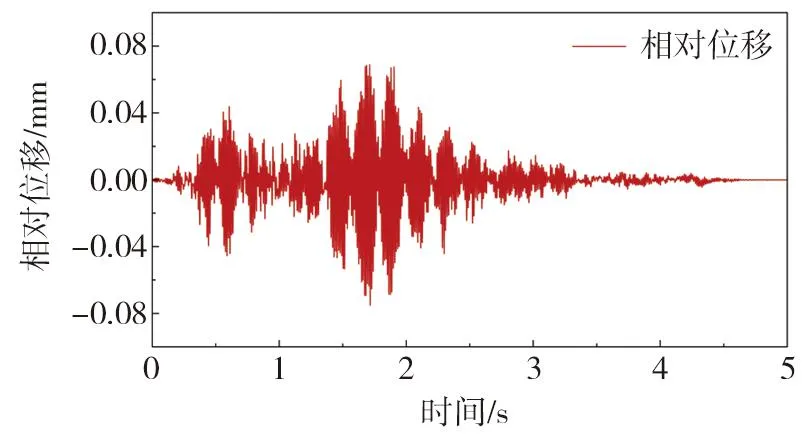
图4 配重螺杆两端相对位移 Fig.4 Relative displacement of both ends of the weight screw

3 缩尺模型设计方法验证

对于这种受力特征不明确且空间效应显著的新型异型拱桥的建模,若采用实体单元建模存在节点过多且不易修改、计算时间过长等缺点。因此本设计采用ABAQUS软件对缩尺桥建立了梁单元模型并开展了对比分析,其中拉索与主梁相应节点间采用耦合约束,后横梁与拱脚实际连接位置相互耦合,暗柱与所处拱肋节段节点采用绑定约束。拱肋与主梁分别通过附加节点荷载与均布荷载实现人工质量的模拟。支座约束通过弹性连接输入换算刚度值进行模拟,桥墩与拱脚底部节点约束全部自由度,假定其与振动台面完成有效固定,有限元模型如图5所示。

图5 有限元模型示意图Fig.5 Schematic diagram of finite element model

3.1 动力特性对比分析

通过原桥模型与缩尺桥模型动力特性分析,前10阶自振频率如表5所示。经对比可以发现前10阶自振频率最大误差不超过7%,其中第一阶误差仅为0.79%,第五阶扭转振型存在相对较大误差的原因应为原桥模型采用梁格法建模,与缩尺桥在扭转刚度上存在一定偏差。结果表明:建立的动力缩尺模型设计合理且能够较好的表征原桥的自振频率的预设结果。原桥模型与缩尺桥模型前5阶振型对比如图6所示。通过对比前5阶振型可以发现:缩尺桥模型的前5阶振型形状均与原桥模型相同,且均无局部振型,故本动力模型能较好地反映出的原空间异形拱桥的动力特性。

表5 原型结构与缩尺模型频率对比Table 5 Comparison of frequencies of prototype structure and scaled model

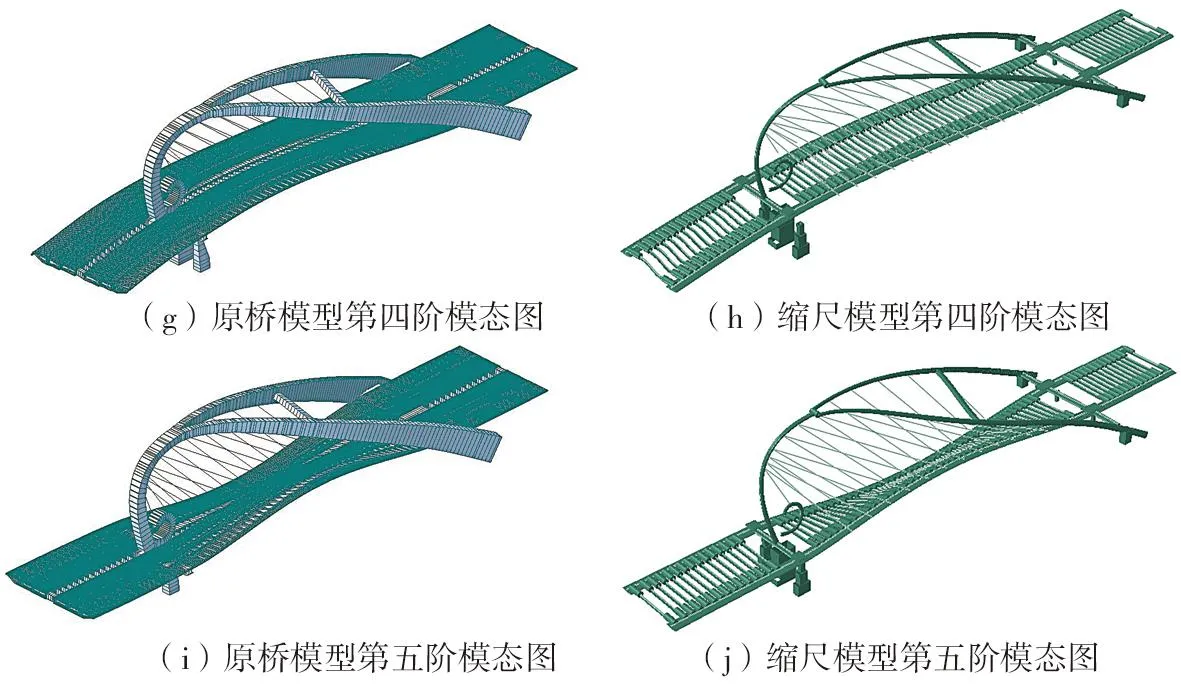
图6 原桥模型和缩尺模型模态对比Fig.6 Modal contrast of prototype structure and scaled model

3.2 动力响应对比分析

本模型动力响应验算选用原桥安评地震波与按时间相似比和加速度相似比换算的缩尺安评地震波分别进行原桥模型与缩尺模型的动力时程分析,并对比关键位置的横向位移峰值以及内力峰值响应。选取原地震波与换算地震波如图7所示。

图7 安评地震波Fig.7 Seismic ground wave of safety assessment

3.2.1 关键位置内力响应

由于缩尺模型相对于原桥结构来说,其质量小于重力相似率下的换算相似质量,属于欠配重体系,因而在对比时程分析结果时,本节排除静力影响,只对比动力时程的结果。拱脚单元与风撑单元的原桥换算内力时程曲线和缩尺模型桥内力时程曲线的对比如图8和图9所示,12对吊杆在地震作用下剔除成桥索力的内力峰值对比,如表6所示。可以发现在安评地震波的横向地震动作用下模型桥可以较好地再现桥梁在地震下的内力状态。

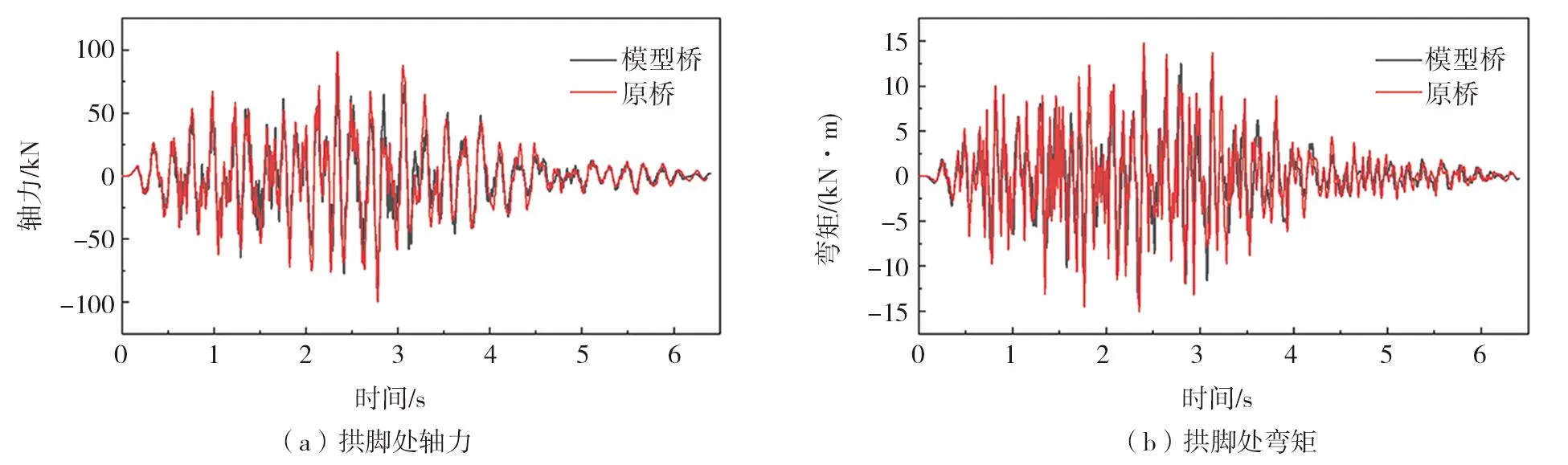
图8 拱脚内力时程对比Fig.8 Comparison of the time history of the arch foot internal force

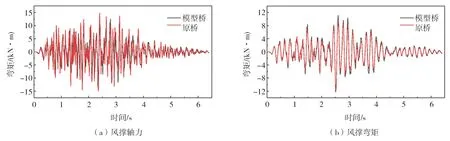
图9 风撑内力时程对比Fig.9 Comparison of the time history of the wind brace internal force

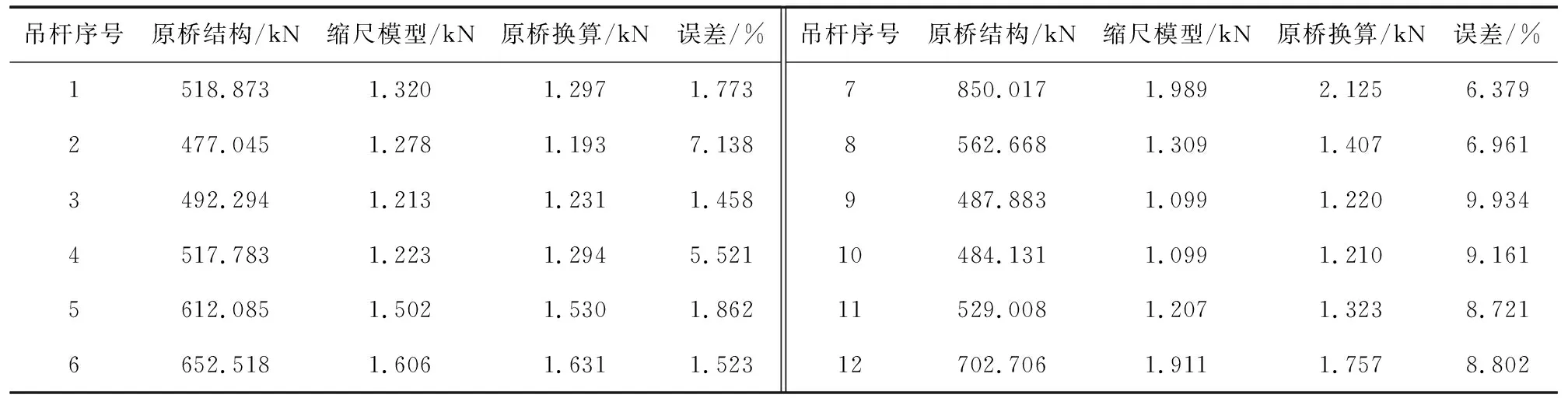
表6 吊杆内力峰值对比Table 6 Comparison of peak values of boom internal force

3.2.2 节点位移响应

为对比动力作用下的位移响应,分别选择主梁与拱肋部分关键节点对比其地震动下位移峰值,拱顶节点与主梁跨中节点的原桥换算位移时程曲线和缩尺模型桥位移时程曲线的对比如图10和图11所示。关键节点横向位移响应峰值对比如表7所示。支座横向相对位移峰值对比如图12所示。可以发现在安评地震波作用下模型桥可以较好地再现桥梁在地震下的位移状态。综合以上两方面动力响应的对比,验证了在动力作用下缩尺模型设计的有效性。

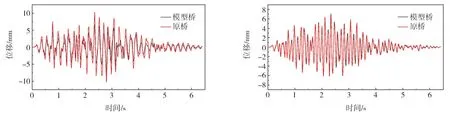
图10 拱顶横桥向位移图11 主梁跨中横桥向位移Fig.10 Lateral displacement of the vault Fig.11 Lateral displacement of the girder of middle span

表7 关键节点横向位移峰值对比Table 7 Comparison of peak values lateral displacement of key nodes

图12 支座横向相对位移峰值对比Fig.12 Comparison of peak values of lateral relative displacement of supports

3.2.3 节点加速度响应

对于振动台阵试验,各节点加速度应作为主要验证对比,在安评地震波横向加载下,缩尺模型与原桥模型的拱肋与主梁各关键节点横向加速度最大响应值的对比如图13所示。其中主梁部分最大误差为3.5%,出现在中跨主梁跨中位置,拱肋部分最大误差为4%,出现在拱顶位置。通过对比可以看出,结构节点在接近振动台支撑位置时,其加速度误差明显小于远离支撑的节点误差,主要原因是缩尺模型在动力作用下存在尺寸效应,在整体刚度矩阵较小位置尺寸效应显著,但误差均在5%以内,可以表明缩尺模型在加速度响应上可以较好地反映出预设加速度的相似关系。