跨断层工程输入地震动模拟及地震响应
2024-03-13胡进军盛兆琦谢礼立邹育麟
胡进军,盛兆琦,谢礼立, 邹育麟
(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;2. 地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080; 3. 四川沿江攀宁高速公路有限公司,四川 西昌 615000)
0 引言
由于地震动和地表破裂的共同作用,位于断层破裂带附近的工程具有较大的破坏风险[1]。自1999年土耳其Kocaeli、Duzce地震以及我国Chi-Chi地震造成跨断层桥梁严重破坏以来,跨断层桥梁的脆弱性越来越受到地震工程界的关注[1-4]。研究认为,跨断层桥梁的损伤与断层两侧地震动的空间变化以及不连续的位移错动有关,使桥梁承受显著的差异位移[5-6]。此外,断层破裂产生的脉冲效应和永久位移也是造成跨断层结构破坏的重要原因[7]。尽管抗震设计规范中提议应尽量避让活动断层,但由于交通规划的需要以及断层分布的不确定性,跨断层桥梁和隧道的修建将不可避免[2]。
目前,跨断层工程的抗震研究中,对断层区域地震动的特征和跨断层结构地震响应的认识不够充分,相应的抗震设计方法也不完善。合理的输入地震动是研究跨断层结构地震响应的前提[2],由于目前全球范围内很难找到地表断裂两侧非常近距离的一对强震记录,而现有的近断层记录在进行基线校正时,采用高通滤波会去除永久位移等低频特征[3]。此外,由于现有强震台站间距远超桥梁跨径,不同台站的近断层记录不能体现断层两侧地震动的空间变异性。
为了解决输入地震动的问题,研究人员提出了一些人工模拟断层地震动的方法。其中,确定性方法和随机方法是模拟地震动的常用方法,但因其各自的局限性,很难直接用于断层地震动的模拟[7]。近年来,一些研究人员在混合模拟方法中引入等效脉冲模型来模拟断层地震动,将拟合的脉冲模型作为地震动的低频分量叠加到原始记录的高频分量中,模拟结果与近场地震动吻合,被用于断层区域地震动的模拟[3,8-11]。但这种方法需要实际的地震动记录作为基础,仅适用于假定滑动均匀分布的走滑断层[9]。例如,PARK等[8]和YANG等[9]将实际的远场记录或近场记录的高频成分与脉冲模型相结合,利用脉冲模型替代近断层地震动的长周期成分,生成破裂断层附近的宽频带地震动。曾聪等[10]研究跨断层独塔斜拉桥的非线性地震响应时,将选取的近断层地震动滤波后与低频分量拟合的等效脉冲模型在时域叠加,实现输入地震动的模拟。由于近断层记录的匮乏和模拟断层类型的单一,限制了这种方法的应用。为此,研究人员基于断层物理模型提出了一些新的模拟方法来避免上述问题。UCAK等[12]采用离散波数法和随机有限断层法模拟跨断层桥梁的输入地震动,并进行地震响应分析。LIN等[6]研究跨断层简支梁桥的地震倒塌机理时,分别采用格林函数法和随机有限断层方法计算地震动的低频和高频分量。张凡等[13]为了揭示跨倾滑正断层桥梁的地震响应规律,构建断层的物理模型并得到其滑动的空间非均匀分布[14],并基于断层破裂物理过程的混合方法生成断层两侧含永久位移的宽频地震动。这种方法物理机制明确,考虑震源、传播路径和场地条件等全过程的影响,较为真实地反映断层破裂的整个过程,但模拟结果依赖物理模型的准确性[13]。
除上述两类方法外,研究人员提出了基于目标位移的基线校正方法恢复近断层记录的永久位移特征。例如,JIA等[2]对Chi-Chi地震断层两侧的近断层记录以不同的目标位移进行基线校正,并基于位移的地震激励原理,对跨断层悬索桥进行动力时程分析。ZHANG等[3]和LIN等[15]使用简化的基线校正方法分析永久位移幅值对跨断层桥梁抗震性能的影响。基线校正的方法仅考虑了永久位移的影响,忽略了断层两侧地震动的其他特征,且高度依赖实测记录。
本文在上述方法的基础上提出了一种基于断层物理模型和等效脉冲模型的混合模拟方法,考虑了震源特性、场地条件、脉冲效应和永久位移以及地震动空间变异性等特征,且不依赖于匮乏的近断层记录。根据模拟结果对跨断层悬索桥进行动力时程分析,揭示其地震响应特征。
1 断层地震动的模拟
跨越活动断层的工程结构会受到近场方向性效应、滑冲效应以及上下盘效应的影响[1,7],同时,断层破裂产生的永久位移以及破裂带两侧地震动的空间变异性也会对其地震响应产生显著影响[6-9]。典型跨断层桥梁示意图,如图1所示。本文通过地质勘察资料、安评报告和场地模型建立桥址处的断层模型,采用随机有限断层方法和等效脉冲模型分别模拟地震动的高、低频分量,并构建地震动空间变异性的转换矩阵,将滤波后的高、低频分量在时域叠加,经转换矩阵后得到断层两侧的输入地震动。

图1 跨断层桥梁地震作用示意图Fig.1 Schematic diagram of the seismic effect for fault-crossing bridge
1.1 基于断层模型的高频地震动模拟
本文以西南地区的一座跨断层悬索桥为研究对象,桥址位于构造活动强烈的断裂带,发震断层以走滑型为主,最大发震震级为Mw7.0,由地质勘察资料确定断层长度约为40 km,走向330°,倾向北东,倾角70°。根据经验公式以及地质勘察资料建立断层模型[16],输入参数的取值如表1所示。

表1 断层模型参数Table 1 Fault model parameters
地震动的高频分量具有很强的随机性,BERESNEV等[17]在随机点源法的基础上提出了考虑断层几何信息的随机有限断层法,可在整个频率范围以及工程所需的距离上进行地震动的模拟[13,17],其计算公式为[14]
(1)
式中:Nl、Nw分别为沿断层面的长度和宽度方向的子断层数量;Δtij为第ij个子断层破裂的滞后时间;aij为子断层破裂引起的观测点的地震动时程。根据建立的断层模型,计算出断层两侧桥址处的高频地震动,并进行0.08~30 Hz带通滤波处理,部分结果如图2所示。
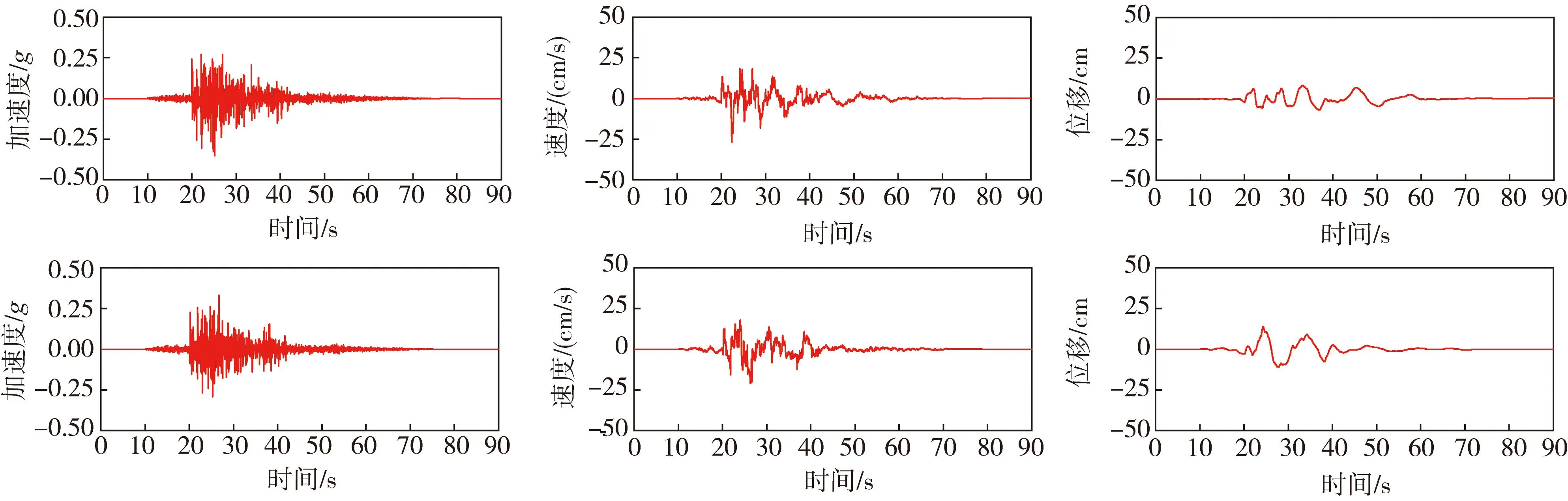
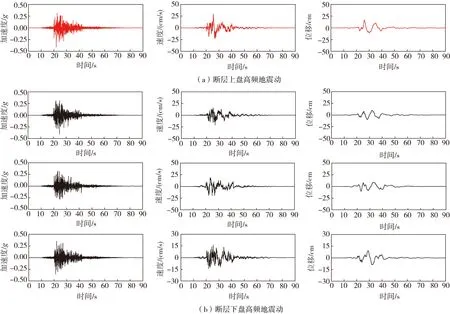
图2 高频地震动的模拟结果 Fig.2 Simulation results of high frequency ground motion
1.2 基于等效脉冲模型的低频地震动模拟
断层破裂产生的脉冲效应对结构影响显著[18],其中破裂方向性效应会导致大幅值、长周期的双向速度脉冲,断层相互错动产生的滑冲效应导致滑动方向的阶跃状永久位移和单向速度脉冲[7,19-20]。近年来多项研究表明,等效脉冲模型可以模拟近断层地震动的脉冲特征[8-10,20],通过将实测地震动记录与表示近断层低频(长周期)成分的等效脉冲相结合,生成断层破裂带附近的宽频带地震动[8-11]。本文利用走滑断层2种脉冲效应相互解耦的特点,采用不同的等效脉冲模型分别模拟断层法向和平行向的脉冲特征。为了统计近断层地震动脉冲参数间的相关性,从BAKER[21]基于PEER NGA-West2强震数据库识别的脉冲型地震动数据集中选取走滑断层地震动记录66组,其部分记录的基本信息如表2所示。
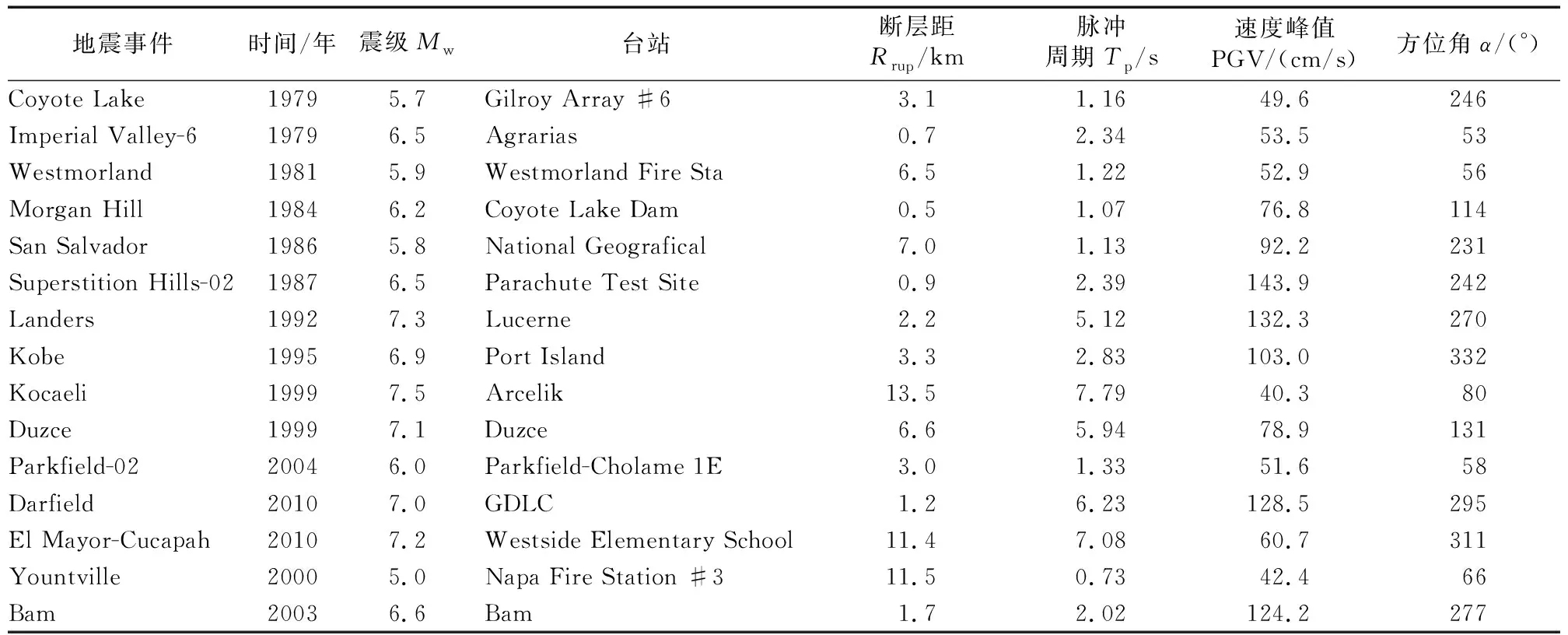
表2 选取的部分走滑断层脉冲型地震动记录Table 2 Selected strike slip fault pulse-type ground motions
1.2.1 断层法向分量
采用MAVROEIDIS等[20]基于大量近断层强震记录提出的等效脉冲模型模拟走滑断层法向的方向性效应脉冲,具体的表达式为
(2)
式中:A为脉冲幅值;fp为脉冲频率;φ为相位;γ为脉冲特征的参数;t0为脉冲的峰值时刻。
脉冲模型各参数由经验预测模型和随机有限断层方法模拟的地震动确定。HALLDRSSON等[22]经研究发现脉冲幅值A≈(0.85~1.00)PGV,并指出PGV的衰减与震级的相关性较弱。为了定量确定脉冲幅值的取值,CORK等[23]提出了PGV与断层距Rrup的衰减关系,如图3(a)所示。由此可根据目标点位与断裂带的距离确定出等效脉冲参数A,如式(3)所示:

图3 脉冲参数的经验拟合公式Fig.3 Empirical fitting formula for pulse parameters
(3)
脉冲周期TP与矩震级Mw密切相关,CORK等[23]依据近断层地震动数据库,通过最小二乘拟合得到式(4)所示的线性关系为
logTP=-2.90+0.50Mw(σ=0.12)
(4)
本文对表2选取的近断层地震动进行线性回归分析,得到脉冲周期TP与震级Mw的统计公式,如式(5)和图3(b)所示。
logTP=-2.81+0.49Mw(σ=0.27)
(5)
计算得到的判定系数R2为0.79,经检验回归系数的P值远小于0.01,因此,可采用该模型确定TP。
YANG等[9]研究发现参数γ和φ的取值可根据走滑断层法向地震动分量的波形特征确定,即由初始位移和最终位移为零确定,通过公式推导得到式(6)所示的确定准则。本文结合YANG等[9]、曾聪等[10]以及LI等[18]的研究结果发现,φ值的大小决定主脉冲的形状,γ影响次脉冲的幅值和周期,γ的最佳取值范围为[1,2]区间,并且φ在[0,2π]的范围内根据波形的不同可分为六类脉冲。脉冲峰值时刻t0一般取t0≥γTP/2[9],可根据模拟的高频地震动的速度时程峰值时刻进一步校准。
(6)
1.2.2 断层平行向分量
永久地面位移是断层相互错动导致的地面同震变形[3],主要沿断层滑动方向,是导致跨断层桥梁震害的原因之一[1-2]。因此,本文采用KAMAI等[24]提出的含永久位移项的脉冲模型模拟断层平行向地震动的低频脉冲特征,其表达式为
(7)
式中:Dsite为永久构造位移;Tf为正弦波周期;t1为滑冲阶跃开始的时刻,KAMAI等[24]将t1设为S波脉冲到达的时间。
尽管正确识别和表征滑冲效应和永久位移对于评估结构响应非常重要,但目前针对该领域的研究较少。由于缺乏具有永久位移的近场地震动记录以及从加速度记录中提取阶跃位移的局限性,对永久阶跃位移的表征是一项难题[25]。目前永久地面位移Dsite可以通过地质测绘、断层挖槽和钻探等方法获得特定点位的断层偏移。当缺乏这些地质勘查数据时,可使用预测模型确定,SCHIAPPAPIETRA等[25]基于新发布的近场强震动记录数据集(near-source strong-motion records, NESS),采用扩展基线校正技术(extended baseline correction technique, EBASCO)恢复永久位移,建立考虑震级、破裂距离、断层倾角和断层类型等参数的预测模型,其结果与震后观测值一致,可用于地震危险性分析。其表达式为
(8)
式中:Dsite为永久位移的大小,即Rrup、Mw、δ分别为断层距、震级和断层倾角;HW为用于指定场地位于上盘或下盘的虚拟变量;NF和TF为指定断层类型的虚拟变量,分别表示正断层和逆断层;dBe和dWes为事件间和事件内残差;其余参数为拟合系数。
YANG等[9]通过假设上述两类脉冲模型确定的永久位移幅值和脉冲幅值分别相等,推导得到Tf的表达式如式(9)所示:
(9)
参数Δt可通过走滑断层法向和平行向脉冲起始时刻的时间差确定,其表达式如式(10)所示:
(10)

1.3 地震动的空间变异性
地震波在传播的过程中受到行波效应以及非均匀地形的影响,场地不同位置的地震动存在差异[26]。这种空间变化被称为地震动空间变异性,主要是由部分相干效应、局部场地效应和行波效应引起,可能会严重加剧结构的地震破坏[27]。跨断层桥梁所处场地在断层破裂带两侧不连续且地质构造复杂,更应考虑到地震动的空间变异性。
地震动的空间变化常用相干函数进行描述,并据此建立非一致激励下的地震动随机场模型,但普通场地采用相干函数得到的不同激励点间的位移差异较小[28],这与断层两侧地震动的特征完全不符[7,29],而且目前针对断层区域尚未建立可靠的地震动相干函数,因此,无法采用此方法描述断层两侧地震动的空间变异性。但走滑断层两侧地面位移具有错动方向相反但幅值大小相同的特点[4,7-9],这一特性也在震后测得的GPS位移记录中得到了验证[12]。此外,在美国Imperial Valley地震中发震断层两侧台站的地震动记录中也能发现走滑断层两侧永久位移“等幅反向”的特征。因此,本文根据走滑断层两侧地震动平行向分量“等幅反向”,法向分量具有连续性的特征模拟其空间变化,同时还考虑行波效应对结构的不利影响。其中行波效应的计算中视波速的取值至关重要,范重等[26]通过研究地震波在单一土层和多土层之间的传播规律,提出了视波速的简化计算方法,将多土层简化为均质土层,由等效均质土层剪切波速的加权平均值结合震源深度和震中距得到视波速,计算公式为
(11)
(12)
本文通过对走滑断层两侧地震动差异性的研究以及视波速的简化计算方法,建立式(13)所示的转换矩阵,实现断层两侧地震动的空间变异性。矩阵的每个元素表示一条输入地震动,其中FNA和FPA分别为断层A侧的法向和平行向的地震动分量,FNB和FPB为断层B侧的法向和平行向的地震动分量。
(13)
将每一项元素具体展开为高频地震动与低频脉冲的叠加,式(13)可进一步表示为
(14)
式中:f(t)为等效脉冲模型模拟的低频脉冲分量;ah(t)A和ah(t)B为基于断层物理模型模拟的断层A侧和B侧高频地震动;Δt为行波效应引起的时间滞后。
2 模拟结果与验证
2.1 地震动模拟结果
模拟的地震动时程如图4所示,由图可知,断层法向和平行向的地震动时程具有方向性效应和滑冲效应的速度脉冲特征,断层平行向的位移时程体现永久位移特征。断层法向地震动分量在断层两侧保持连续性,平行向分量的速度脉冲和永久位移在断层两侧反向对称。

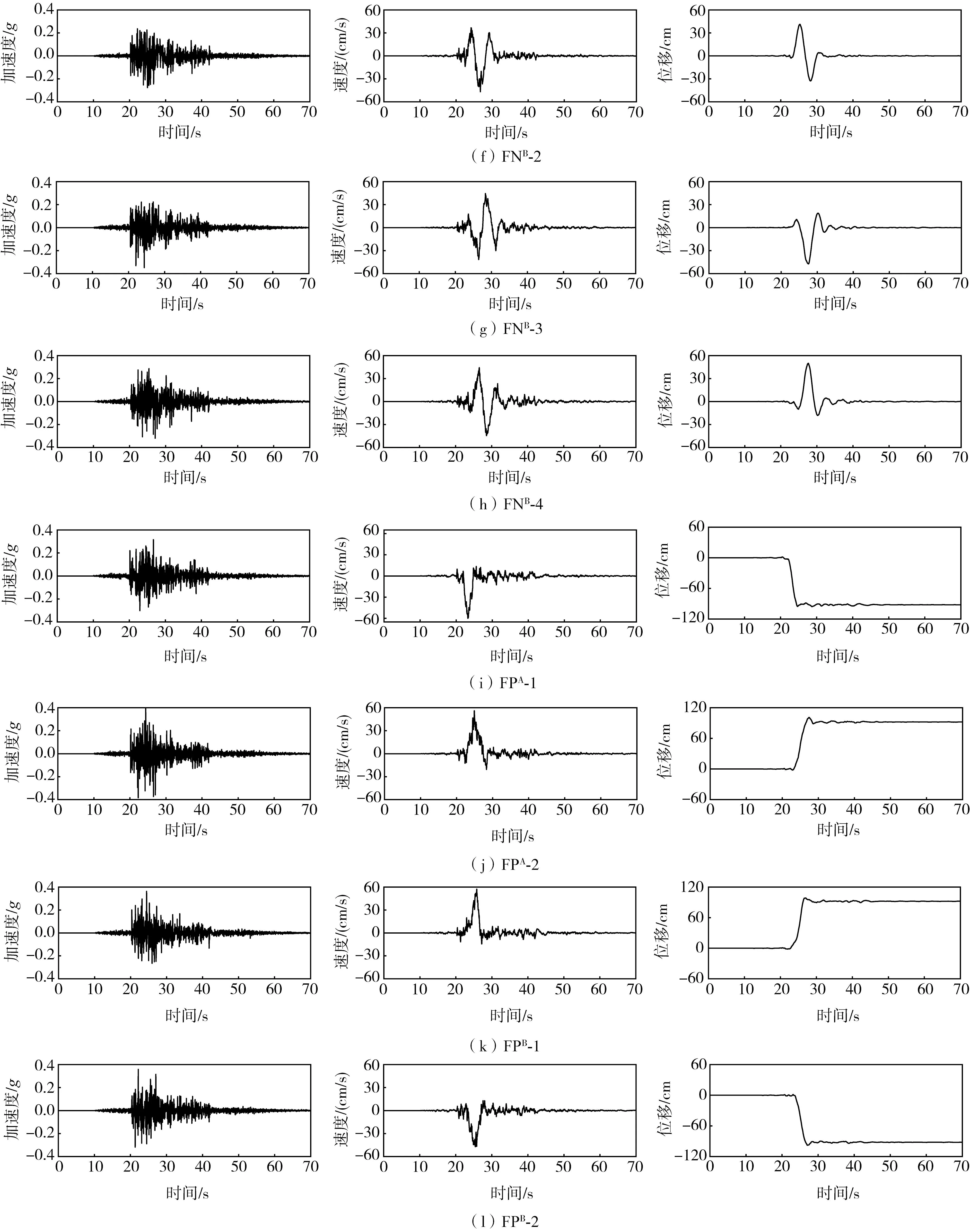
图4 断层两侧法向和平行向的模拟地震动Fig.4 Simulated ground motions in the normal and parallel directions on both sides of the fault
2.2 模拟结果的验证
将模拟的断层两侧的地震动与ABRAHAMSON等[30]提出的地震动预测模型(ground motion prediction equation, GMPEs)进行比较,该模型考虑了震级、断层类型、断层倾角、断层距、断层破裂宽度、上下盘效应、VS30以及场地非线性的影响,同时还考虑模型的区域特征,根据日本和我国VS30和非弹性衰减项(Q值)的差异,得到适合特定区域的预测模型。模型的输入参数如表3所示,其表达式为
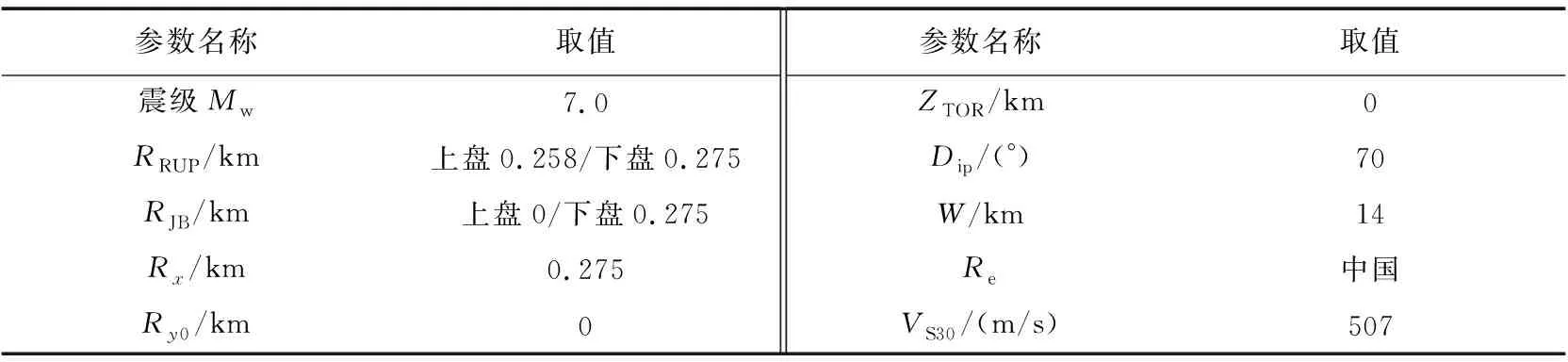
表3 GMPE ASK14模型的输入参数Table 3 Input parameters for the GMPE ASK14 model
lnSa(g)=f1(M,RRUP)+FRVf7(M)+FNf8(M)+FASf11(CRJB)+
f5(Ŝa1180,VS30)+FHWf4(RJB,RRUP,Rx,Ry0,W,Dip,ZTOR,M)+
f6(ZTOR)+f10(Z1,VS30)+Re(VS30,RRUP)
(15)
式中:M为震级;RRUP、RJB、Rx、Ryo分别为断层的不同距离;FRV、FN、FAS分别为逆断层、正断层和余震的标志;Ŝa1180为VS30=1180 m/s处的谱加速度;FHW为上盘效应的标志;Dip为断层倾角;W为断层破裂宽度;ZTOR为破裂顶部的深度;Z1为VS=1.0 km/s时的深度;Re为区域特征项。
模拟地震动与预测模型拟加速度反应谱的对比,如图5所示。由图可知,模拟的结果(上下盘各6次水平地震动)大致在预测值的标准差范围内。但在长周期范围内,一些周期点的模拟结果超出了预测值范围。这是由于计算点位非常接近地表破裂,因为滑冲效应导致长周期分量突出,而建立GMPE ASK14预测模型的数据库中的地震动记录分布在一个较大的地震区域,不能准确地反映离断层很近的局部情况[6]。

图5 模拟的地震动与GMPE ASK14拟加速度反应谱的对比(5%阻尼比)Fig.5 Comparison of the elastic pseudo-acceleration response spectra (5% damping ratio) between the simulated ground motions and the GMPE ASK14
断层两侧的地震动本质上为一组近断层地震动,2个观测点位于断层两侧并距断层很近,具有与近断层地震动相同的特征[7,29]。为了进一步比较模拟方法的合理性,本文将模拟的断层一侧的地震动与PEER NGA-West2数据库中选取的近断层记录进行对比,其结果如图6所示。由图可知,模拟结果与近场实测记录的地震动时程具有良好的相似性,选取的地震动信息如表4所示。

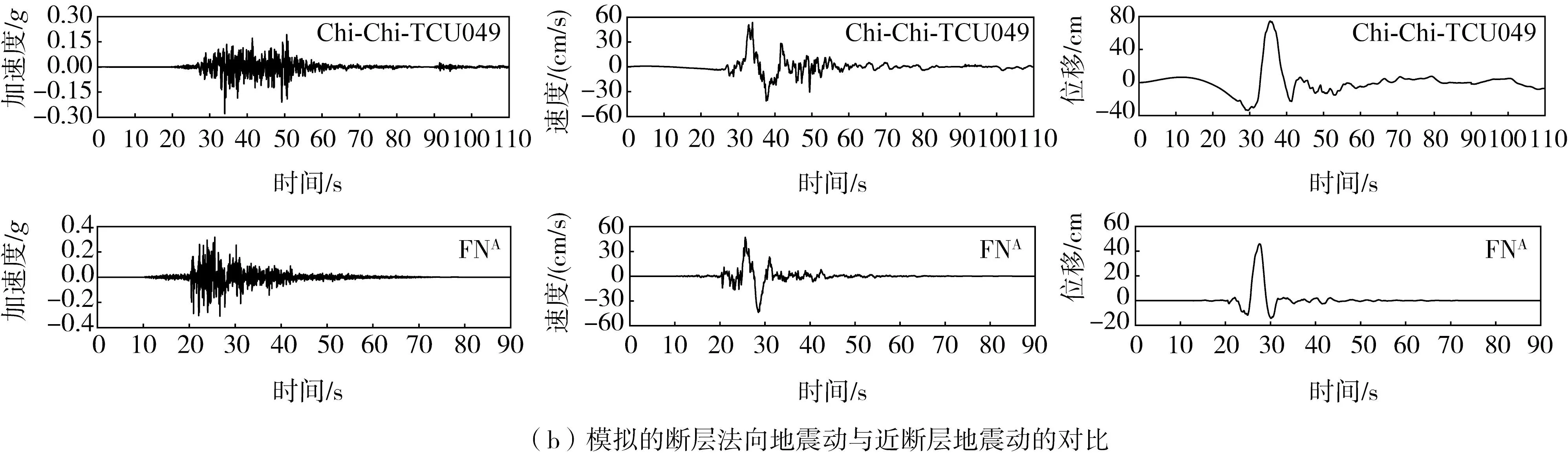
图6 模拟地震动与近断层记录的对比Fig.6 Comparison of simulated ground motion with near-fault records

表4 选取的近断层地震动信息Table 4 Selected near-fault ground motion information
3 跨断层悬索桥地震反应分析
跨断层桥梁一般采用结构形式简单、易于修复的简支梁桥跨越断层,以减少震后修复的困难和成本[2,12]。许多大跨度桥梁需要跨越断层密布的西部山区,由于缆索承重桥梁对断层破裂位移有良好的适应性,能减轻脉冲效应和永久位移对动力响应的影响,是跨越活动断层的合理选择[2]。为了研究模拟的断层地震动激励下跨断层桥梁的地震响应规律,本节以一座实际跨断层悬索桥为研究对象,基于断层物理模型和等效脉冲函数的混合模拟方法构建输入地震动,进行非一致地震激励下的动力响应分析。
3.1 有限元模型的建立
本文以中国西南地区的一座跨断层悬索桥为研究对象,桥址位于V形河谷区域,场地构造复杂,桥梁整体跨越走滑断层破裂带。两座桥塔分别位于破裂带两侧,高度分别为103、140 m,采用钢筋混凝土门式结构,桥梁主跨为550 m,主梁采用钢桁梁形式。有限元模型的材料和单元特性的详细信息如表5所示。基于通用有限元软件OpenSees建立全桥的三维有限元模型,如图7(a)所示。其中桥塔和主桁采用三维弹性梁柱单元模拟,主缆和吊索采用空间桁架单元模拟,采用壳单元模拟桥面板。实际工程中桥梁跨越断层具有一定的角度,桥梁跨断层的角度和位置如图7(b)所示,跨断层角度对其地震响应影响显著,以90°左右跨越时,桥梁受力最为合理[3,10-11]。为了便于研究,假定桥梁垂直跨越断层,并忽略桩-土相互作用以及河谷地形地震放大效应,模拟的地震动在塔底沿顺桥向和横桥向进行输入。

表5 材料和单元特性Table 5 Materials and element characteristics

图7 三维有限元模型Fig.7 3D finite element model
3.2 地震反应分析
跨断层桥梁的内力和位移响应不仅受断层两侧不同地震动的影响,还要受到断层破裂位移的影响[1],分析时常采用基于位移的地震动激励原理[2]。本节研究了桥塔、主梁以及主缆的结构响应,分析跨断层角度和位置,以及永久位移对其地震响应的影响。
桥梁跨越断层的角度和位置的不同,会使其地震响应产生显著差异。本文以断层迹线与桥梁轴线的夹角θ为参数,分别计算不同角度下的地震响应。同时设立2种工况研究跨断层位置的影响,工况A:1#桥塔和2#桥塔分别位于断层两侧,桥梁垂直跨越断层,采用非一致激励。工况B:1#桥塔和2#桥塔分别位于断层同侧,采用一致激励。根据2.1节模拟的结果,经计算后,确定以图4中的FNA-2、FPA-1、FNB-2和FPB-1输入为最不利工况,后文的地震反应分析均以此工况作为输入。不同跨断层角度和位置下的结构响应,当跨越角度在0°到90°范围内,塔底剪力、弯矩以及主梁位移均随着跨断层角度的增加而减小,而在90°到180°范围内,随跨越角度的增大而增大,如图8所示。因此,在设计时以垂直跨越断层为最佳方案。在跨断层效应的影响下,工况A桥塔、主梁的位移和内力响应显著大于工况B,图8中工况A的1#桥塔和2#桥塔的纵向位移相较于工况B最多增长了80%和73%。表6中2座桥塔工况A的塔底剪力、弯矩和扭矩相较于工况B分别增长了38.99%(24.92%),112.4%(117.24%),63.32%(73.91%)。此外,由于上下盘效应的影响,2#桥塔塔底内力明显大于下盘的1#桥塔。由此可见,跨断层桥梁的地震响应显著大于近断层桥梁。

图8 不同跨越角度和位置时的结构响应Fig.8 Structural response of different crossing angles and positions

表6 不同跨断层工况下的塔底内力Table 6 Internal force of tower bottom under different fault-crossing conditions
断层破裂会在地表产生永久破裂位移,增加结构的地震响应。对于跨断层桥梁而言,断层两侧的永久位移使其发生严重破坏甚至垮塌[12-13]。为了研究断层永久位移的影响,本节在断层法向输入地震动不变的情况下,通过改变脉冲参数Dsite的取值,模拟出具有不同永久位移幅值的断层平行向地震动,进行地震响应分析。随着Dsite的增加,跨断层桥梁的地震响应相应增大,其中残余内力和残余位移增幅显著,进一步证明了地面永久破裂位移是造成跨断层桥梁破坏的重要原因,如图9所示。
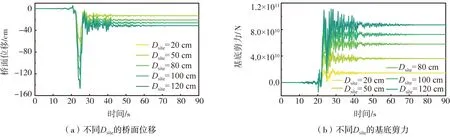
图9 不同Dsite的地震响应Fig.9 Seismic response of different Dsite
4 结论
为解决跨断层工程输入地震动的问题,本文在现有方法的基础上提出一种混合模拟方法,采用随机有限断层方法和等效脉冲模型分别模拟地震动的高、低频分量,并构建地震动空间变异性的转换矩阵,将滤波后的高、低频分量在时域叠加,经转换矩阵后得到断层两侧的输入地震动。以实际的跨断层工程结构为例,基于OpenSees建立其有限元模型,根据模拟的地震动时程进行地震响应分析,得到以下结论:
1)基于断层物理模型并引入等效脉冲,考虑了震源特性、场地条件、脉冲效应和永久位移特征,构建转换矩阵,实现走滑断层两侧地震动空间变异性的模拟。该方法弥补了确定性方法和随机方法的不足,解决了以实测记录作为基础的局限性,能适用于不同地区,不同断层距、不同震级的断层两侧输入地震动的模拟。
2)与经验地震动预测模型比较的结果表明,本文模拟结果在预测模型的误差范围内,能较好地模拟断层两侧的输入地震动,模拟地震动在时程以及频谱特性上,均与近场地震动具有良好的吻合性。
3)在断层地震动的激励下,跨断层桥梁产生较大的地震响应,存在残余内力和残余位移,这是造成其破坏的重要原因。跨越断层的角度和位置对桥梁的地震响应有显著影响,当桥轴线与断层迹线的夹角越小,其结构响应反而越大,在设计时建议以垂直跨越走滑断层为最佳方案。此外,断层破裂产生的永久位移对跨断层悬索桥的动力响应有显著影响,其地震响应随着永久破裂位移的增大而显著增加。
