基于控制灵敏度的微电网有功无功协调二次控制方法
2024-03-13龚伟孙丹李逸源
龚伟,孙丹,李逸源
(1.福建华电福瑞能源发展有限公司华安水力发电厂,福建 漳州 363800; 2.南京国电南自电网自动化有限公司,南京 211153; 3.华电(华安)供电有限公司,福建 漳州 363800)
0 引言
近年来,为解决分布式发电的就近消纳问题,微电网成为学术界与工程界的研究热点。由于分布式电源大多直接接入中低压等级的微电网中,线路的电阻与电抗大小十分接近,其有功-频率控制、无功-电压控制不再呈现明显的解耦关系,为微电网的实际工程应用带来巨大挑战[1-3]。
在微电网一次控制领域中,为了应对有功、无功控制间的耦合问题,学者们提出了虚拟阻抗[4-7]、虚拟同步发电机[8-12]等方法,实现了对微源有功-频率(P-f)下垂、无功-电压(Q-V)下垂的解耦控制。然而,在微电网二次控制领域中,有关有功、无功控制耦合问题的讨论比较有限。文献[13-14]针对微网系统频率实时控制问题,在多代理分层混合控制模型中嵌入一种基于Q学习的智能算法进行二次调度的功率缺额计算,采用模糊化方法和粒子群优化算法实现二次调度的功率分配;文献[15]针对并网型微网系统,提出使用滚动平均法、分段平均法计算调节功率,从而调整微源出力,恢复频差,实现耦合点的定功率控制。文献[16]提出一种微电网最优功频特性等值模型与动态矩阵控制方法相结合的二次频率调节策略,通过滚动优化控制快速恢复系统频率。文献[17]针对孤岛直流微电网需要独自维护系统母线电压稳定、完成精确功率分配的情况,提出了含母线电压补偿和负荷功率动态分配的协调控制策略。
控制灵敏度是将电网模型线性化后得到的控制变量与状态变量之间的近似关系,其最早应用于大电网协调二级电压控制之中[18-19]。然而,大电网协调二级电压控制中采用的控制灵敏度是在忽略了有功与无功耦合的情况下推导出来的,在微电网中,有功与无功耦合较强,需要重新推导考虑了有功-无功(PQ)交互影响的控制灵敏度。
本文提出了一种基于控制灵敏度的微电网有功无功协调二次控制方法。首先,基于微电网一次控制后的稳态模型,推导得到二次控制的控制灵敏度;然后,基于控制灵敏度建立微电网有功-无功协调二次控制的二次规划模型;通过求解此二次规划模型得到微电网二次控制的调节量。
1 微电网二次控制的系统模型
微电网二次控制是在一次控制的基础上,通过调节一次控制的参考值,实现微电网的频率/电压控制。因此,二次控制模型是基于一次控制稳态方程的微电网潮流模型建立的。微电网潮流模型采用极坐标形式,
式中:Pi,Qi分别为第i个节点的注入有功和无功功率,发电机的为正,负荷的为负;Vi,Vj分别为第i个节点和第j个节点的电压幅值;θij为第i个节点和第j个节点电压的相角差;Gij,Bij分别为节点导纳矩阵的实部和虚部;N为全网节点数目。
1.1 主从控制模式下的微电网稳态模型
主从控制系统是由一个V/f控制微源和多个PQ控制微源构成的微电网一次控制系统。
对于采用V/f 控制的微源节点,二次控制的控制对象为该节点的电压幅值和频率。由于在主从控制模式下频率控制是独立的,与其他系统变量不存在耦合关系,因此本文不考虑该模式下的频率控制。此外,由于V/f 控制的控制变量端口电压幅值(VVf)已经出现在潮流方程中,因此,不用额外增加描述V/f 控制的稳态方程,直接在该节点潮流方程的基础上,令VVf为可调节的控制变量,令有功出力(PVf)、无功出力(QVf)为待求的系统状态变量即可。
式中:xVf,uVf分别为V/f 控制微源节点的状态变量和控制变量。需要指出的是,V/f控制微源节点的相角应当设置为常数0以维持方程个数与状态变量个数相等。
同理,对于PQ 控制的微源节点,由于其控制变量有功出力(PPQ)、无功出力(QPQ)已经出现在潮流方程中,不用额外增加描述PQ 控制的稳态方程,直接在该节点潮流方程的基础上,令PPQ,QPQ为可调节的控制变量,令PQ 控制微源的端口电压(VPQ)、端口电压相角(θPQ)为待求的系统状态变量即可。
式中:xPQ,uPQ分别为PQ 控制微源节点的状态变量和控制变量。
对于其他不存在一次控制的负荷节点和联络节点,待求的系统状态变量为节点电压幅值和相角。
1.2 对等控制模式下的微电网稳态模型
对等控制系统主要是由P-f 下垂、Q-V 下垂控制的微源构成的微电网一次控制系统。考虑此控制模式下微电网的稳态情况时,需在潮流方程的基础上增加方程组
式中:f为系统运行频率;Pdroop,Qdroop,Vdroop分别为下垂控制微源实际运行的有功出力、无功出力、端口电压幅值;P0,Q0,V0,f0分别为下垂控制中设置的初始运行点有功出力、无功出力、端口电压幅值、输出频率;KP,KQ分别为P-f下垂系数和Q-V下垂系数。
在下垂控制的基础上,微电网二次控制通过上下平移下垂曲线来实现频率电压的调节。因此,对于采用下垂控制的微源节点,状态变量(xdroop)与控制变量(udroop)为
式中:θdroop为下垂输出相角。需要指出的是,在对等控制模式下的微电网稳态模型中,由于引入了系统频率f作为未知的状态变量,使得上述方程组中状态变量个数比等式方程个数多1 个,因此需要通过指定某一节点的相角为常数0来维持系统方程组的解的唯一性。
此外,在对等控制模式的微电网中也有可能存在PQ 控制的微源,其控制变量与状态变量的定义与章节1.1中的描述相同。
2 控制灵敏度计算
要对频率、电压进行统一的二次调节,必须计算准确的控制灵敏度。根据章节1 的描述,微电网二次控制的系统模型可统一表述为
式中:x为系统中所有状态变量;u为二次控制所调节的控制变量。当微电网采用主从控制模式时,式(6)即为式(1)所述形式。当微电网采用对等控制模式时,式(6)为式(1)与式(4)联立的形式。
计算控制变量u对系统状态变量x的控制灵敏度,首先在式(6)中两边同时对u求导,得到如下线性方程组
式中:∂g/∂x为式(6)的雅可比矩阵;∂x/∂u为待求的控制灵敏度;∂g/∂u为各方程对各控制变量求导形成的矩阵。通过简单的矩阵运算可以得到控制灵敏度的计算公式为
3 有功无功协调的二次控制算法
在得到控制变量对系统状态变量的控制灵敏度后,需要建立一种算法机制对微电网的有功、无功进行协调的二次控制。本文通过求解二次规划的方式来实现这一控制算法。以对等控制模式的微电网为例,其二次规划的模型为
式中:ΔPPQ,ΔQPQ,ΔV0,Δf0均为二次规划模型的优化变量,分别代表PQ控制的有功出力调节量、PQ控制的无功出力调节量、下垂控制的初始电压调节量、下垂控制的初始频率调节量;f,V,Pg,Qg分别为实测的系统频率、节点电压、微源有功出力、微源无功出力;fN和Vref分别为系统额定频率和节点电压参考值;Pg,all和Qg,all分别为当前微电网中微源的总有功出力和总无功出力;p和q分别为各微源的有功分配系数和无功分配系数;Vmax,Vmin,Pg,max,Pg,min,Qg,max,Qg,min分别代表节点电压上下限、微源有功出力上下限、微源无功出力上下限;α,β,γ,λ分别为目标函数中频率项、电压项、微源有功项、微源无功项的权重系数;C为控制灵敏度,其右下角标代表控制变量,右上角标代表状态变量。
式(9)中目标函数包含了4 项:第1 项的意义为控制系统频率在额定值附近;第2 项的意义为控制各节点电压在参考值Vref附近;第3 项的意义为按分配系数p来分配各微源的有功出力;第4 项的意义为按分配系数q来分配各微源的无功出力;其中Vref,p,q由上级优化调度指定。
综上所述,微电网有功无功协调的二次控制流程如图1所示。
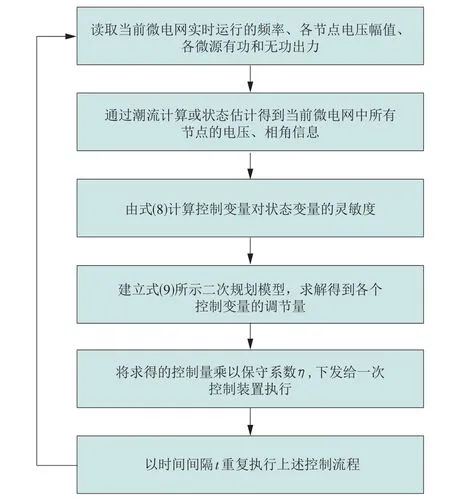
图1 微电网有功无功协调的二次控制流程Fig.1 Flow chart of coordinated secondary control for active and reactive power in microgrid
4 算例分析
4.1 仿真系统简介
以某实际海岛微电网系统对上述微电网有功无功协调的二次控制流程进行仿真验证,系统接线方案如图2 所示,其中,线路及变压器参数见表1。在之后的仿真计算中,此系统的初始潮流计算参数见表2。
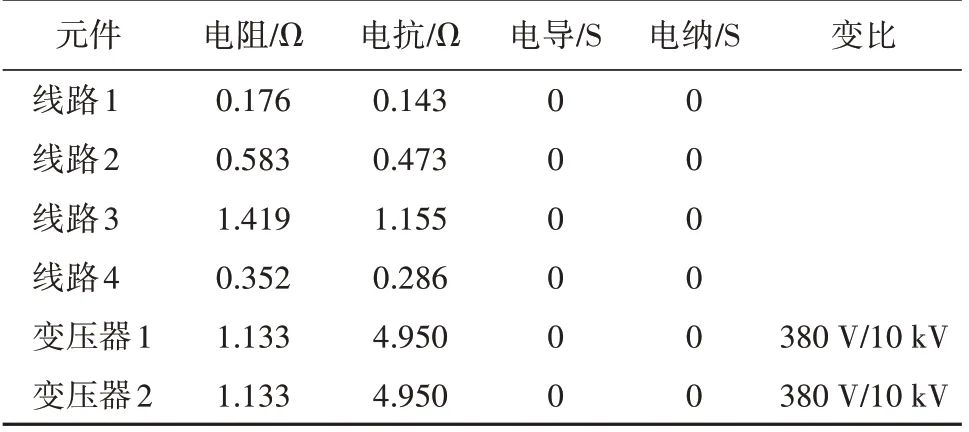
表1 某海岛微电网系统线路及变压器参数Table 1 Parameters of lines and transformers in the islanded microgrid
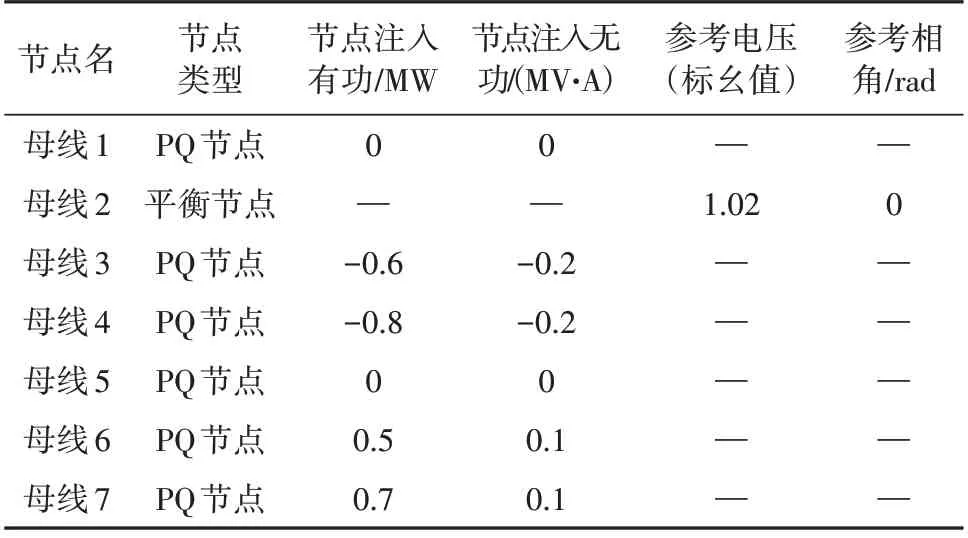
表2 某海岛微电网系统初始潮流参数Table 2 Initial power flow parameters of the islanded microgrid
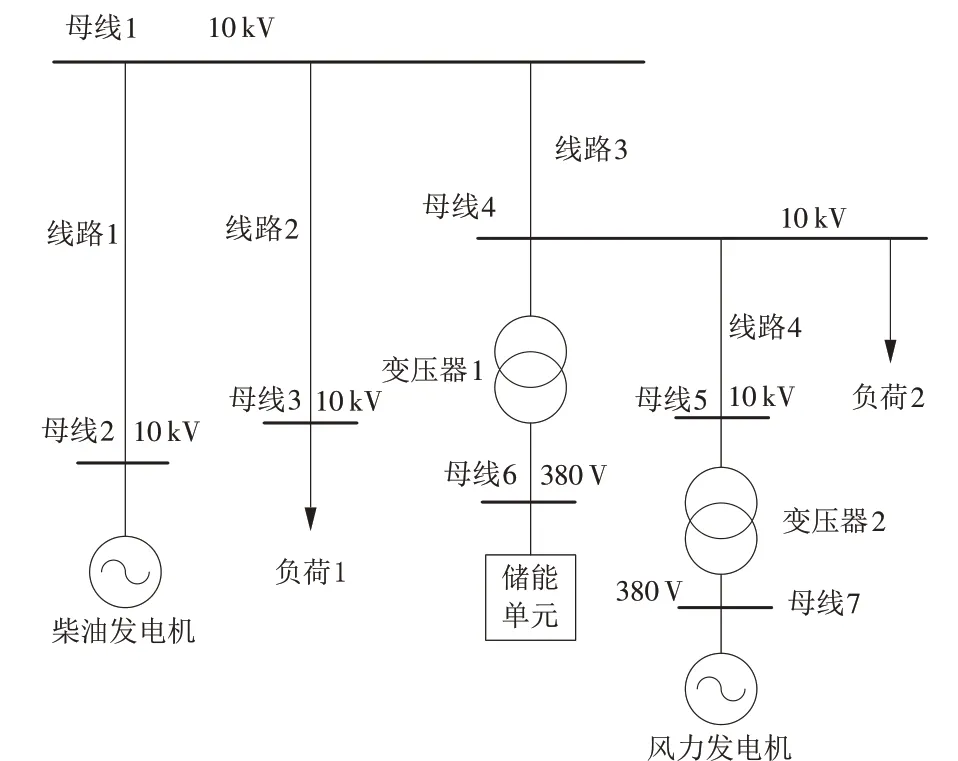
图2 某海岛微电网系统接线方案Fig.2 Wiring of an islanded microgrid
多微源场景下控制的复杂性会有所提高。假设当前控制场景为风能充足的情况,风力发电机也作为可控微源参与二次控制[20]。各微源的有功无功上下限见表3。
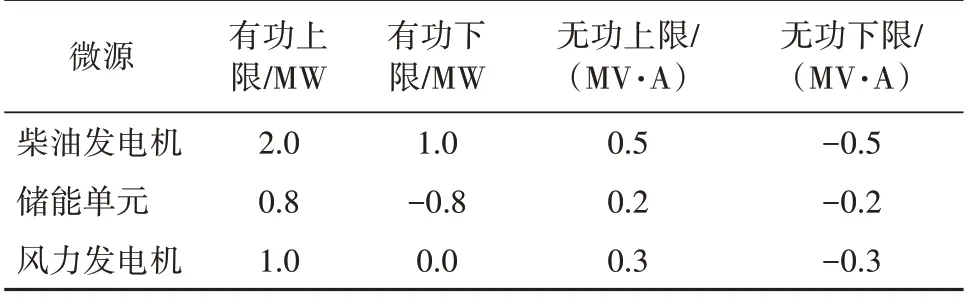
表3 微源有功无功上下限约束Table 3 Upper and lower bounds of active and reactive power of micro-sources
4.2 控制灵敏度分析
主从控制模式下,假设柴油发电机为主控制节点,储能单元和风力发电机为从控制节点。在表2所示的初始潮流状态下,控制变量对状态变量的控制灵敏度见表4。表4 中:V1—V7为母线1—7 的电压;Pd,Qd,Vd分别为柴油发电机的有功功率、无功功率、端口电压;Pw,Qw为风力发电机的有功功率、无功功率;Ps,Qs为储能单元的有功功率、无功功率。

表4 主从控制模式下的控制灵敏度Table 4 Control sensitivities in master-slave control mode
从表4 中可以看出,各控制节点的有功出力和无功出力对各节点电压控制的灵敏度大小十分接近,因此,在微网中进行二次电压控制时,需要综合考虑有功调节与无功调节的影响。
对等控制模式下,令各微源的P-f 下垂系数和Q-V 下垂系数(标幺值)均为0.05,同样以表2 中的数据为初始潮流运行点,控制变量对状态变量的控制灵敏度见表5(控制变量中的下标0 表示初始点)。
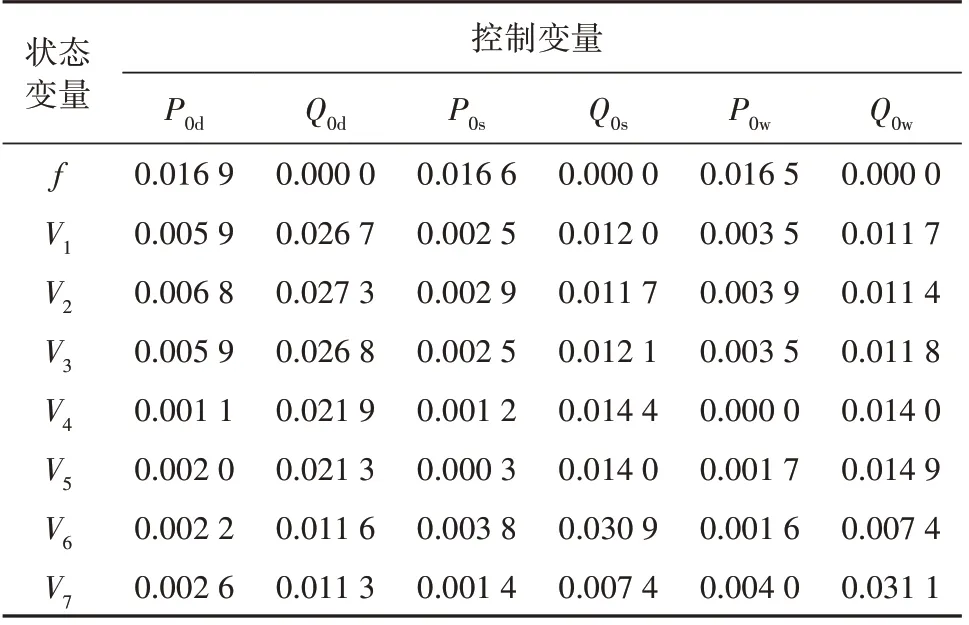
表5 对等控制模式下的控制灵敏度Table 5 Control sensitivities in peer control mode
为了方便比较,将控制变量初始频率f0和初始电压V0转换为了初始有功P0和初始无功Q0。从表5中可以看出,在对等控制模式下,由于在就地的下垂控制中已经实现了P-f 控制与Q-V 控制的解耦,因此,在此基础上进行二次控制时,有功调节与无功调节的耦合性将大为减弱。但是,需要指出的是,Q-V 控制灵敏度大致为P-f 控制灵敏度的3~5倍,在某些控制场景下,有功调节仍然会对电压造成一定影响,具体分析在下一节中给出。
4.3 控制性能比较
比较2种频率电压二次控制方法的效果。方法1 为本文提出的有功、无功统一调节的频率电压协调二次控制方法;方法2 为有功、无功独立调节的V/f 二次控制方法。所谓的方法2 就是在式(9)中令有功对电压的控制灵敏度为0,令无功对频率的控制灵敏度为0,即让P-f和Q-V进行独立调节。
在主从控制模式下,假设在10 s 时负荷1 与负荷2(见图2)的有功、无功需求同时增长了10%,将引起系统节点电压下降。忽略一次控制的动态过程,假设二次控制的调节周期为10 s/次,在方法1与方法2 的控制下,节点4 的电压变化曲线如图3所示。
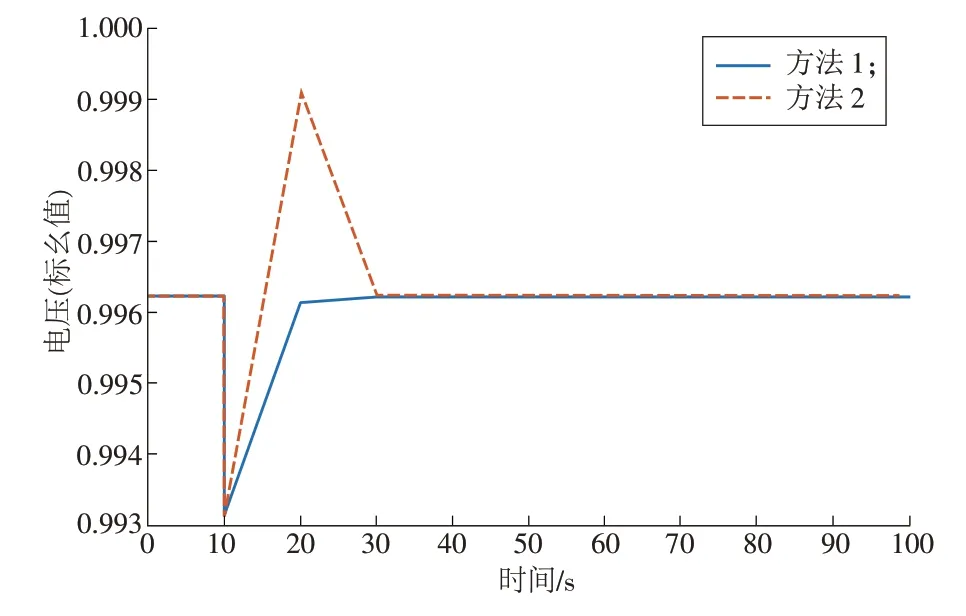
图3 主从控制模式下2种控制方法节点4的电压曲线Fig.3 Voltage curves of bus 4 under two control methods in master-slave control mode
从图3中可以看出:方法2在第1次控制时出现了很大的超调,这是由于控制过程中忽略了有功调节对电压的影响而造成的;而方法1 只用一次调节就将节点电压控制在了稳态值附近。因此,在主从控制模式下,实施有功、无功统一协调的二次控制具有明显的优势。
在对等控制模式下,假设在10 s 时负荷1 与负荷2的有功、无功需求同时增长了10%,引起系统节点电压和频率下降。忽略一次控制的动态过程,假设二次控制的调节周期为10 s/次,在方法1与方法2的控制下,系统频率和节点4 的电压变化曲线如图4—5所示。
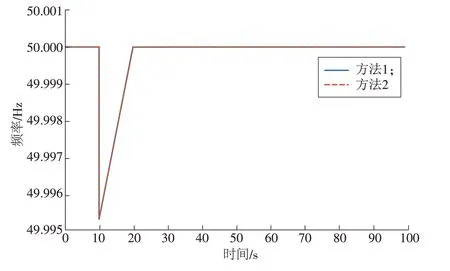
图4 对等控制模式下2种控制方法的频率曲线Fig.4 Frequency curves under two control methods in peer control mode

图5 对等控制模式下2种控制方法所得节点4电压曲线Fig.5 Voltage curves of bus 4 under two control methods in peer control mode
从图4—5 中可以看出,方法1 和方法2 的控制效果差别不大,这是由于在对等控制模式下,有功-频率控制与无功-电压控制的控制灵敏度已经基本解耦。因此,在对等控制模式下进行二次控制时,有功无功统一与独立的差别不大。
5 结论
本文提出了一种基于控制灵敏度的统一调节有功无功的微电网频率电压二次控制方法,通过某实际海岛微电网的仿真分析可得出以下结论。
(1)主从控制模式下,调节有功出力和无功出力对节点电压的控制灵敏度大小十分接近,而在对等控制模式下,有功调节与无功调节呈现较为理想的解耦状态。
(2)在主从控制模式的微电网中,本文提出的频率电压协调二次控制方法能有效提高控制的准确性和稳定性。由于微电网的二次控制通常是在微电网能量管理系统中实现,基于控制灵敏度的二次规划模型的求解计算量很小,其在能量管理系统中的计算时间对控制结果的影响几乎可以忽略不计。
