基于变分模态分解改进生成对抗网络的短期风电功率预测
2024-03-13江善和李伟徐小艳王德凯
江善和,李伟,徐小艳,王德凯*
(安庆师范大学 a.电子工程与智能制造学院;b.经济与管理学院,安徽 安庆 246011)
0 引言
风能作为一种无污染、储量丰富且分布广泛的可再生能源,受到广泛关注[1-2]。然而,风能属于间歇性能源,其对天气的依赖性和不稳定性带来的高随机性和低可预测性极大地影响了大型电网集成风力发电系统的安全性和稳定性[3]。由于大规模电力储存仍然成本高昂,有效的风能预测成为应对风力发电在不同规模电网中高渗透的一个解决方案。因此,风电功率预测对促进风电并网至关重要[4-5],是将风力发电与不同规模的现有电网相结合的关键技术。而风电功率预测中的短期预测,即预测未来30 min~6 h 的输出,对风电调度和控制等具有重要指导作用[6-7]。
风电功率预测从模型原理角度可分为4 类:物理模型、传统统计模型、基于人工智能的模型和混合模型[8-11]。混合模型通过组合不同类型的模型来更好地表征风速或风电功率波动的特点。文献[12]提出了将信号滤波或分解方法与其他方法有效结合的预测模型;Shukur 等[13]提出了基于自回归移动平均的卡尔曼-人工神经网络混合模型,实验结果表明该算法能有效减小预测误差;Giorgi 等[14]提出了结合小波分解与最小二乘支持向量机的不同区间的风速预测建模方法,实例验证所提的方法预测效率较高。
深度学习方法因具有显著的能够挖掘数据中的非线性关系和识别数据抽象特征的能力,在许多领域得到了广泛应用[15-17]。Goodfellow 等[18]提出的生成对抗网络(Generative Adversarial Networks,GAN),已在计算机视觉和自然语言处理等领域取得良好的应用效果[19]。Aldausari 等[20]提出的ForGAN 首次应用于预测任务中,随后GAN 成功应用于金融领域等时间序列预测问题[21],但其在风电功率预测领域的应用却很少。
本文针对风电数据强非线性和序列不稳定性问题,提出一种变分模态分解改进GAN(Variational Mode Decomposition-GAN,VMD-GAN)的风电功率短期预测方法,并应用于提前1 h 的短期风电功率预测。该方法以深度学习中的GAN 为基本框架:首先,通过VMD 方法,将非平稳复杂序列风电数据的预测任务转化为多个较为平稳简单序列风电数据的预测任务;其次,改进传统GAN,重新设计了激活函数和损失函数,利用深度学习GAN 强大的拟合非线性能力,提高风电数据的预测性能;最后,利用Bengaluru 某风场的真实数据对上述方法进行仿真分析,并进行了算法关键参数的敏感性分析。结果表明,改进方法有效地提高了风电输出功率的短期预测精度。
1 VMD
VMD 是由Dragomiretskiy 和Zosso 提出的用于信号分解的技术[22],它具有自适应、完全非递归的特点,能够对非平稳信号进行有效分解和处理。VMD 可以自适应地匹配各模态的中心频率和带宽,可以实现固有模态分量(Intrinsic Mode Function,IMF)的分离,进而得到给定信号的有效分解成分[23]。VMD 相比经验模态分解(Empirical Mode Decomposition, EMD),具有更坚实的数学理论基础,不存在其他分解模型的限制,如:EMD 存在端点效应和模态分量混叠的问题,无法正确处理噪声;小波方法存在硬带限值等问题。使用VMD 可将原始序列的非稳定和非线性分散在子序列中,得到相对平稳的子序列,降低了下一步处理的难度。
风电数据一般受风速、风向等多因素影响,是由多种成分组成的非平稳信号。VMD 算法首先构造变分问题,假设原始信号f被分解为K个分量,保证分解序列为具有中心频率带宽的模态分量,同时各模态的估计带宽之和最小,约束条件为所有模态之和与原始信号相等,则相应的约束变分表达式为
式中:K为模态数;{uk}和{wk}为分解后第k个模态分量及中心频率;δ(t)为单位脉冲函数。
求解式(1),引入Lagrange 乘法算子λ,将该问题转化为非约束变分问题,得到增广Lagrange 表达式
式中:α为二次惩罚因子。
利用交替方向乘子迭代算法和傅里叶等距变换方法等,交替寻优迭代uk,wk和λ,优化得到各个模态分量和中心频率分别为
式中:γ为噪声容限,即信号分解的保真度要求;̂分别为u,f,λ对应的傅里叶变换。
VMD算法的具体步骤如下。
2 GAN
GAN 是利用博弈论中的零和博弈估计生成模型的新框架。GAN 由生成器和判别器组成。生成器和判别器的构成不局限于特定的结构或网络。生成器G 将输入的随机噪声转化为生成数据,使生成数据尽可能符合真实样本的特征,从而使判别器D 无法将生成数据与真实样本分开;判别器D 则是将生成器G 产生的生成数据与样本数据分开,输出为判别结果。其结构如图1所示。

图1 GAN结构Fig.1 Structure of a GAN
生成器和判别器的对抗过程可以表述为对V(D,G)的最大最小博弈
式中:G(z)为噪声变量的先验pz(z)在数据空间的映射;D(x)为x来自真实数据的概率;pdata(x)为真实数据的先验。
GAN的训练过程为交替训练判别器和生成器。
首先训练判别器。对于固定的判别器,其输入包括真实数据和生成器产生的数据,判别器判断输入数据是否为真实数据,给出输入为真实样本的概率作为输出。输入真实数据时输出应为1,而输入生成数据时其输出应为0。训练判别器时,应使得输出尽可能接近对应状态下的值,即取使V(D,G)为最大值的D,
式中:pg(x)为生成数据的先验。
其次训练生成器。固定判别器的参数,将噪声z输入生成器,产生生成数据,然后将其与真实数据输入给判别器。对于假数据样本,训练生成器时,应使判别器的输出尽可能接近0,即取合适的G,使V(D,G)取最小值,
由式(8)可得:当pdata(x) =pg(x)时,V(D,G)取最小值。
在训练过程中,生成器和判别器互相对抗,最后接近或者达到纳什均衡,即D*(x)=0.5。此时认为判别器已经无法分辨输入是否为真实的样本数据,同时生成器已经具有产生符合真实样本特征数据的能力。
3 基于VMD改进GAN
在进行短期风电功率预测时,由于风电数据常具有强非线性及非平稳特性,导致预测模型的精度不高,而传统GAN 在训练时容易发生模式崩溃。为解决该问题,设计了VMD-GAN 模型。该模型使用VMD 得到子序列。相比原始序列,其非线性和非平稳性降低,更容易实现预测。通过构造GAN,实现非线性关系的拟合,从而提高模型的精度。
3.1 网络结构
VMD-GAN 的结构可分为3 部分,分别为数据预处理、含VMD 及多个预测器的生成器G、判别器D,其结构如图2所示。
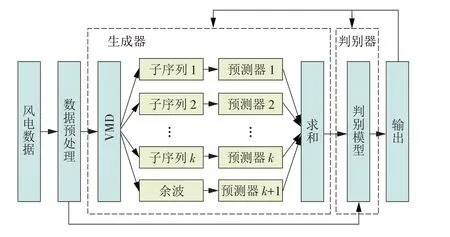
图2 VMD-GAN结构Fig.2 Structure of a VMD-GAN
数据预处理主要是采用三次样条插值方法对数据样本的缺失值进行补缺,然后将其归一化,并将数据改为所需的结构,形成风电功率预测的数据集。
生成器如图2 所示,由VMD 和k+1 个预测器组成,其中k为VMD 分解的阶数。长短期记忆(Long Short-Term Memory,LSTM)神经网络在时间序列预测任务中表现出良好的性能,故生成器中的预测器采用LSTM神经网络作为核心。
本方法改进了生成器的结构,采用分解的思想,使用VMD 分解原始序列,将分解出的子序列送入以LSTM 神经网络为核心的子预测器进行预测,最终将子序列预测结果求和作为预测输出。风电数据经过VMD 后得到k个本征模态函数,再对数据进行处理得到1 个余波,这k+1 组数据具有良好的规律性。将分解得到的数据分别输入到对应的k+1 个子预测器中,得到对应的输出并进行求和作为预测输出,并生成相应的生成数据。考虑到经过VMD 后的数据相比原始数据复杂度降低,可预测性提高,预测子序列相比预测原始序列对于生成器的拟合非线性的能力要求更低,更容易提高预测精度。
VMD-GAN的判别器以LSTM神经网络为核心,判别器作为一个二分类器,其作用是判别输入的数据是否为真实的样本数据。传统的判别器使用卷积神经网络[24],然而在风电功率预测中,LSTM 更适宜处理真实样本中的时间相关性,可以有效降低模型的复杂程度和参数数量,故使用LSTM 作为判别器的核心[25]。
3.2 关键设计
为了解决GAN 存在的模型不稳定问题,本文设计了激活函数和损失函数。激活函数的设计在GAN 模型的构建中发挥关键的作用。风电输出受制于物理和电气性能,其输出有明显的截断特性,而GAN 的生成器的前期预测结果相比实际结果的差距会非常大,使用传统的激活函数会使得模型容易陷入梯度爆炸或梯度消失的状态,因此,设计了一种新的生成器激活函数
式中:l为可调参数。该激活函数的优点在于使模型训练中梯度值虽较小但始终存在,避免了由于模型参数快速变化而导致模型的不稳定。
损失函数的设计也是GAN 模型中的关键之一,恰当的损失函数可以兼顾网络训练速度和网络的稳定性,进而影响网络收敛时的精度。生成器和判别器的作用是完成分类任务,模型设计中常采用交叉熵、均方误差(Mean Square Error,MSE)方法实现有效分类。本文对2种不同的损失函数都进行了实验,结果发现,GAN 的损失函数单独使用二元交叉熵很难使模型稳定,故本文采用交叉熵和MSE 的加权和作为GAN 的损失函数。判别器的损失函数仍然使用二元交叉熵。此时GAN 的损失函数表征输入数据正确分类的平均概率。
3.3 训练过程
VMD-GAN 训练过程选用的优化器为Adam[26],具体训练步骤如下。
(1)初始化生成器和判别器的权重以及优化器的参数,确定激活函数和损失函数的具体表达,准备数据集。
(2)若VMD-GAN算法未满足停止条件,则:1) 更新判别器,固定生成器的参数,将给定的历史数据进行VMD并输入生成器得到相应的生成数据,将其与真实数据输入给判别器,使用优化器更新其权重;2) 更新生成器,从生成器重新产生生成数据,将其与真实数据输入判别器,使用优化器更新其权重。
(3) 计算训练后的生成器在训练集和测试集上的损失,验证此时VMD-GAN是否满足停止条件,如果满足则训练终止,否则重复步骤(2)直至满足终止条件或者达到最大迭代次数。
4 实验及结果分析
4.1 实验参数与设计
本文的模型和算法使用Python 3.9 和TensorFlow 2.10进行实验验证。考虑到风电数据存在长时依赖性,采用的数据集为Bengaluru 风电场某风机2007年1月—2021年7月的风电数据。数据采集为1 次/h,记录的内容除风电功率外还包含风速、风向、气压、环境温度、露点温度、相对湿度等气象数据。实验设计使用前72 h的风电数据预测第73 h的风电功率。首先使用三次样条插值对缺失值进行预处理,处理后总数据共127 315 条,每条数据的形状为72×12,其中前4/5 为训练集,其余作为测试集。
VMD-GAN 模型中生成器由VMD 模块、多个基于LSTM的子预测器、多个全连接层和1个求和器构成。每个基于LSTM 的子预测器由2 层共包含32 个神经元的LSTM 构成,预测器最后一层的激活函数为式(9)的激活函数,前述各个层之间添加了Dropout层防止过拟合,生成器的学习率为0.001;判别器由2 层LSTM、2 个Dropout 层、2 个全连接层构成,学习率与生成器相同。
风电功率预测性能常用的定量评价指标主要有平均绝对误差(Mean Absolute Error,MAE)、MSE、均方根误差(Root Mean Square Error,RMSE)、最大预测误差(δmax)等。MAE,MSE,RMSE 和δmax分别代表预测值与真实值之间误差的均值、方差、标准差和最大值,取值越小表示预测与实际的误差越小,精度越高,预测方法的性能越好。
4.2 实验结果与分析
4.2.1 VMD算法关键参数k值的确定
首先,需要确定VMD 算法中的关键参数k,将k取值由小到大依次分解并分析结果的中心频率,见表1。可看出,取值4 和5 的最大中心频率相似,可以认为在k取值为5 时出现了模态混叠,故确定k取值为4。对应的分解结果如图3所示。可见,原始数据经过分解得到4 个频率和复杂度依次降低的IMF分量和1个余波。

表1 不同k值对应分解结果的中心频率Table 1 Center frequencies of decomposition results made based on different k value
4.2.2 激活函数参数敏感性分析
VMD-GAN 算法中设计的激活函数参数l的取值对算法性能有重要的影响。为选取合适的l值,本文在0.01~0.50 内分别选取若干个数值,在同一数据集上进行性能比较实验,其预测误差结果见表2。可以看出,所设计激活函数参数取值过大和过小均会影响算法的性能,其中l取0.10 时,VMDGAN 的预测性能最佳。此时,VMD-GAN 的预测MSE 最低。l偏离0.10 越多,模型预测MSE 越大。因此,本文的VMD-GAN 算法的激活函数参数l选取0.10。
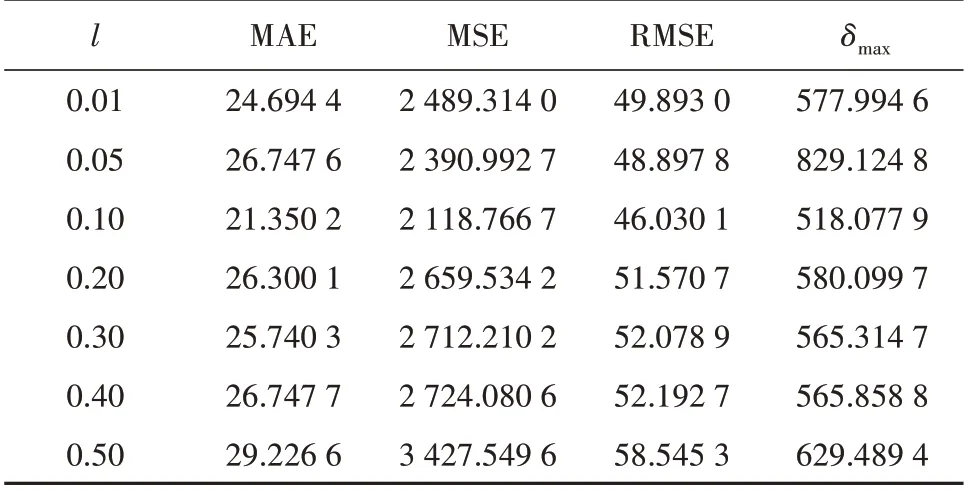
表2 l取不同值时VMD-GAN的评价结果对比Table 2 Prediction results of VMD-GAN with various l value
4.2.3 算法性能比较分析
为进一步验证和比较所提VDM-GAN 方法的预测性能,本文选用短期风电功率预测领域中的4 种模型进行分析:自回归移动平均模型(ARIMA)[27]、引入VMD的ARIMA模型(VMD-ARIMA)[27],LSTM[28]和仅使用生成器部分的模型(VMD-LSTM)[28]。客观评价指标选取常用的定量评价指标MAE、MSE、RMSE 和δmax,并在计算时先对相关结果进行反归一化。针对同一测试集,使用上述各种算法进行实验,获得的客观评价指标,见表3。
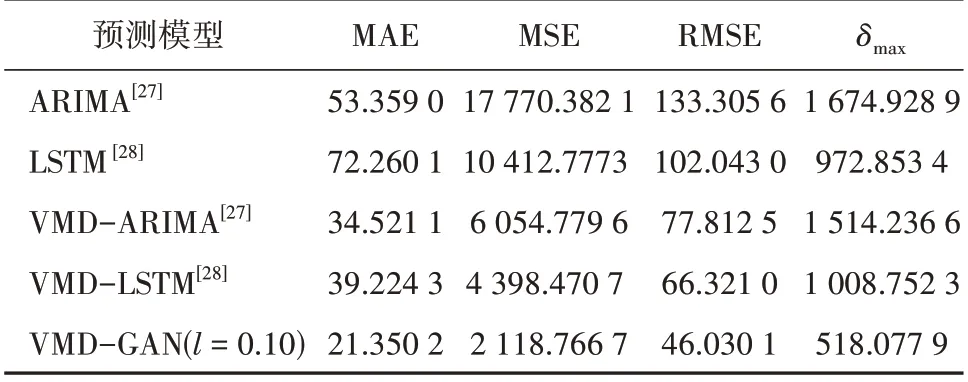
表3 不同预测模型结果对比Table 3 Prediction results of various models
分析表3 可知,对比传统的ARIMA 和LSTM,引入VMD 的VMD-ARIMA 和VMD-LSTM 预测模型的精度得到了提升,但在最大预测误差方面改善不够明显。对比VMD-LSTM 和VMD-GAN,可以发现添加判别器组成的GAN 性能又得到进一步提升,且最大预测误差降低。从4 个指标总体来看,本文所提VMD-GAN 算法最优,VMD-LSTM 和VMD-ARIMA两者性能相近,但均优于LSTM 和ARIMA,其中ARIMA的最大误差最大,LSTM的MAE最大。
同时,将VMD-ARIMA,LSTM,VMD-LSTM 和VMD-GAN 这4 个模型的原始数据和预测结果进行对比输出,其结果如图4 所示。可见,LSTM、VMDLSTM 与VMD-GAN 模型预测结果与实际数据的走势基本相同,预测偏差依次减小,其中VMD-GAN的拟合效果最好,这代表VMD 算法的融入和GAN 的构造提高了模型处理非线性、非平稳风电数据的能力,很好地提高了风电模型的预测精度。
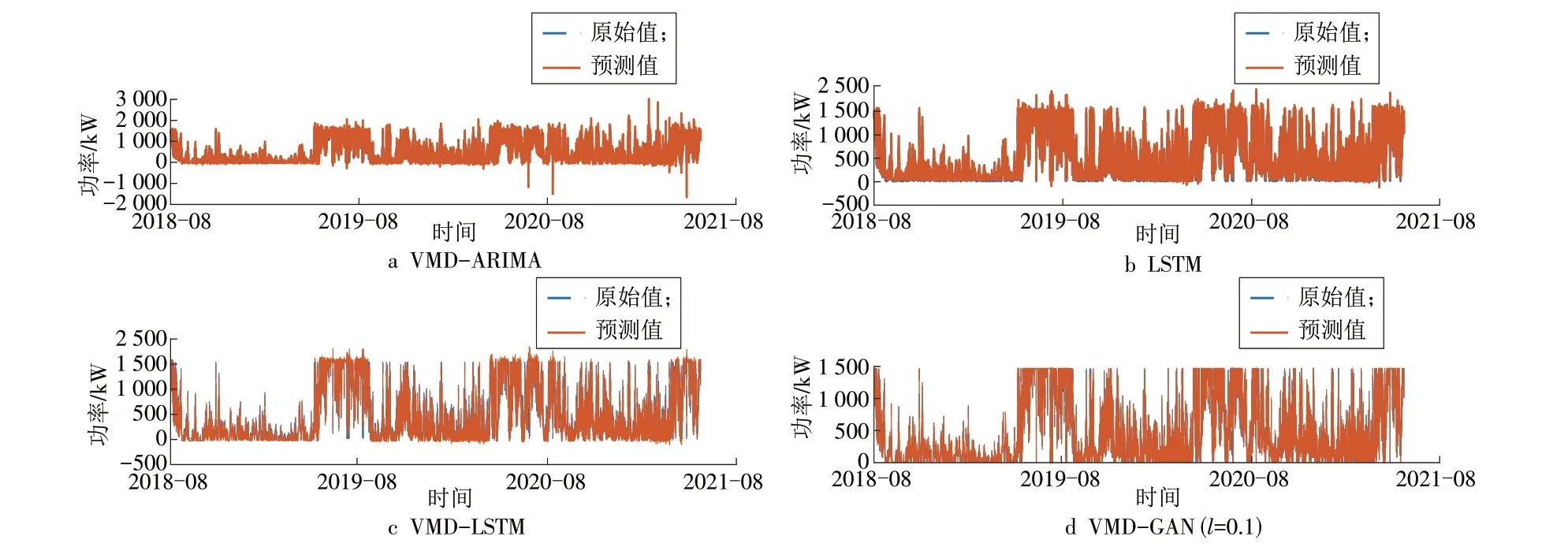
图4 VMD-GAN与其他方法预测结果对比Fig.4 Forecasting results of VMD-GAN and other methods
VMD-GAN 与其他方法的预测结果误差分布如图5 所示。可见,4 种方法的误差分布相似,但是VMD-GAN方法的预测误差更低,其MSE相比LSTM和VMD-LSTM 分别下降79.65%和51.83%,说明预测模型通过构造GAN 后,4 种误差评价指标均大幅降低,能更好地处理风电数据和其中的突变值。实验结果表明,VMD-GAN 模型相较于ARIMA,VMDARIMA,LSTM和VMD-LSTM 法,能够更好地分析和处理风电数据,且预测精度得到极大提高。

图5 VMD-GAN与其他方法预测结果误差对比Fig.5 Forecasting errors of VMD-GAN and other methods
5 结论
针对风电数据非线性强、非稳定的特点,以及传统GAN 容易发生模式崩溃的问题,引入VMD,提出了一种基于VMD 改进GAN 的短期风电功率预测方法VMD-GAN,该方法使用VMD 思想,将复杂序列的预测转化为多个较为简单序列的预测,设计了激活函数和损失函数,解决传统GAN 模型不稳定问题,并对VMD-GAN 方法的关键参数进行了分析。实验结果表明,本文方法取得了良好的预测效果,能够处理强非线性和非平稳特征的短期风电功率预测问题。
