基于增量交换的主动配电网分布式多目标最优潮流
2024-03-13陆文甜
陆文甜
(广州大学 机械与电气工程学院,广州 510006)
0 引言
最优潮流(Optimal Power Flow,OPF)是解决可再生能源调度中电能质量和可靠性问题的主要工具之一。配电层OPF 的目标包括使网络损耗最小化以及使网络运营商和终端用户的经济效益最大化[1-2]。根据优化目标的多样性,集中式多目标OPF(Multi-objective Optimal Power Flow,MO-OPF)算法[3-5]常用来计算分布式电源的最优功率整定值。实际运行中,分布式可再生能源可能由不同的发电运营商控制与管理,受商业隐私、数据保密等限制,不同运营商彼此之间很难共享各自的详实数据,无法实现集中式多目标计算。随着高比例可再生能源接入配电系统,配电网络运营商和能源运营商之间存在竞争与合作的复杂利益关系,不同的利益主体相互制约,如配电网运营商与微电网运营商[6],配电网运营商与分布式发电商[7-9],配电网运营商与消费者个体[10]。在本文中,也存在不同的利益主体,即网络运营商和能源运营商(或终端消费者)。具体来说,配电网运营商的重点是提高电压质量和减少网络损耗,而分布式电源运营商的目标是最大限度地减少停电。
现有MO-OPF 算法研究主要集中于寻找帕累托最优解集,包括各种矢量化或标量化方法,例如,带精英策略的快速非支配排序遗传算法(NSGAII)[3,11]、粒子群优化算法[12]、遗传算法[13-14]、权重法[15]、ε约束法[16]、均衡规划[17]、法线边界交叉法[18]和归一化正态约束法[19-23]。然而,这些多目标方法均需要在一个集中式系统环境下执行,即需要收集所有利益主体的信息,存在不同利益主体私有数据暴露问题。
到目前为止,只有少数研究者从不同利益主体的角度出发提出分布式多目标优化方法。例如,文献[6]提出了一种双层能量管理策略,其中配电网运营商与连接的微电网运营商之间的相互作用用双层规划来描述,微电网运营商之间的相互作用用交互能量博弈矩阵来描述。本文提出一种基于增量交换的主动配电网分布式MO-OPF 算法。首先,基于归一化正态约束法将多目标优化模型转化为一系列单目标优化模型。其次,在能源运营商侧引入辅助等值注入功率变量和目标变量,将集中式多目标最优潮流模型分解为能源运营商侧和配电运营商侧的子模型。最后,基于辅助变量的增量交换,实现能源运营商和配电运营商之间的信息交互,获得与使用集中式优化相同的帕累托最优解。
1 分布式MO-OPF建模
1.1 能源运营商模型
令Nc代表安装有分布式可再生能源的节点集合。对每个分布式可再生能源i∈Nc,其运行目标及约束包括最小化有功缩减量(式(1))、节点的有功和无功注入约束(式(2—3))、分布式电源的有功和无功输出限制约束(式(4—6))。
式中:Pres,i/Qres,i为位于节点i的分布式能源有功/无功功率;为位于节点i的分布式能源等效的有功/无功输出功率;Pav,i为分布式能源最大功率(即预测值)为能源运营商模型的目标函数;Sres,i,φi分别为分布式能源装机容量和最大功率因素角;Pd,i/Qd,i为非分布式电源节点i有功/无功负荷。
1.2 配网运营商模型
配网侧则更多关注网络有功损耗和电压偏移目标。因此,其运行目标及约束包括节点功率平衡方程(式(8—9))、节点有功和无功注入约束(式(10—12))、节点电压和支路功率限制约束(式(13—14))。
式中:fu为配网运营商模型的目标函数,由网损floss和电压偏差fV组成;γ为网损目标与电压偏差目标的折中系数;Pi/Qi为配网节点i注入有功/无功功率;Vi为节点i对应电压幅值;θij为线路ij两端节点相角差;Ps/Qs为配网根节点Ns注入的有功/无功功率,即输配联络线传输的有功/无功功率;为输电线路i,j允许的最大传输功率;为节点i允许的电压最小、大值;Gij+ jBij为配网节点导纳矩阵第i行第j列元素;N为配网节点集合;Ns,N(i)分别为与配网根节点s 和节点i相连的节点集合;L为输电线路集合。
式(7)中目标函数的具体表达式为
式中:Vnom为额定电压,其标幺值为1;gij为配网输电线路ij的电导值。
2 分布式MO-OPF求解算法
使用矢量xu和xc,fu和fc,gu和gc,hu和hc分别为MO-OPF 模型配网侧和能源侧的变量、目标函数、等式约束和不等式约束,上述2 个模型可简化为如下紧凑形式
进一步,对式(17)目标函数进行规格化处理
式中:fu,min/fu,max和fc,min/fc,max分别由单目标优化计算得到。为了产生帕累托最优解集,需要将原多目标优化模型(式(17—19))转化为一系列单目标优化模型,即
式中:j=0,1,2,…,m。式(25)代表基于归一化正态约束法[19]所产生的正交约束集。
求解能源侧优化模型的Karush-Kuhn-Tucker(KKT)最优性条件,可得如下稀疏线性修正方程组
式中:Hi和Ji分布代表海参矩阵和雅克比矩阵;和分别代表扰动KKT条件的残差。
注意到线性方程组式(26)的解可通过求解如下二次规划模型获得
将式(27)代入式(28),可得
式中:Hu和Ju分别为海参矩阵和雅克比矩阵;和分别代表网络侧模型对应扰动KKT条件的残差[24]。
至此,所有原对偶变量修正量均计算完毕。其信息交互示意如图1所示。

图1 网络侧与能源终端侧信息交互示意Fig.1 Information exchange between the network side and user side
3 仿真算例
使用一个修正的IEEE 33 节点配电系统进行仿真。修正的IEEE 33节点配电系统如图2所示,红色方框代表分布式光伏系统。16 个光伏系统分别安装在节点5,7,9,11,12,14,15,16,20,21,23,25,27,29,31 和32。节点5,23,25 光伏系统的可用有功功率为100 kW,节点7,12,14,21,27,31 光伏系统的可用有功功率为200 kW;剩余光伏系统可用有功功率为300 kW。光伏逆变器的功率因素为0.85[10]。网络节点电压幅值上、下限分别为1.04和0.95(标幺值)。目标折中系数γ被设置为0 或1。所有程序均在Matlab 2014a 和Simulink/Matlab 工具中执行,计算机采用DELL Precision T1700 工作站,处理器为Intel(R)Core(TM) i7-4800 MQ,内存为16 GB。
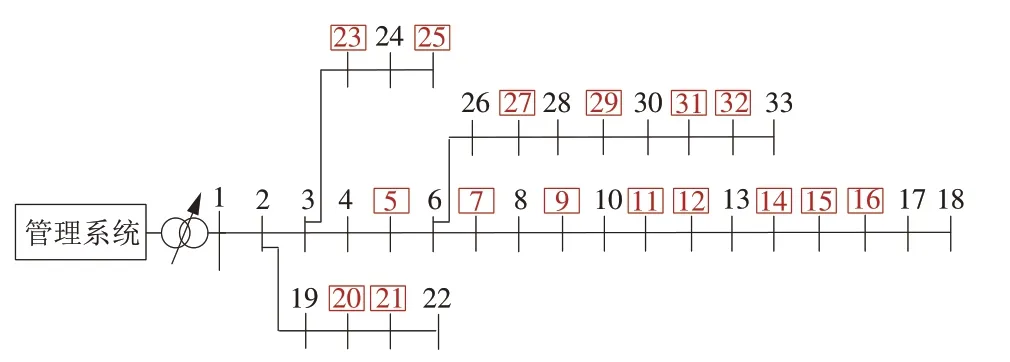
图2 修正的IEEE 33节点配电系统Fig.2 Updated IEEE 33-bus distribution system
所提分布式MO-OPF 的帕累托最优解集如图3所示。利用模糊隶属度和熵权法[25]可获得最佳折中最优解,对目标函数折中参数γ=0 和γ=1 的OPF模型其折中最优点分别位于第12,13 节点。从图3可知,所获得的帕累托前沿与集中式算法所获得的帕累托前沿完全一致,这也验证了所提分布式MOOPF算法的准确性。
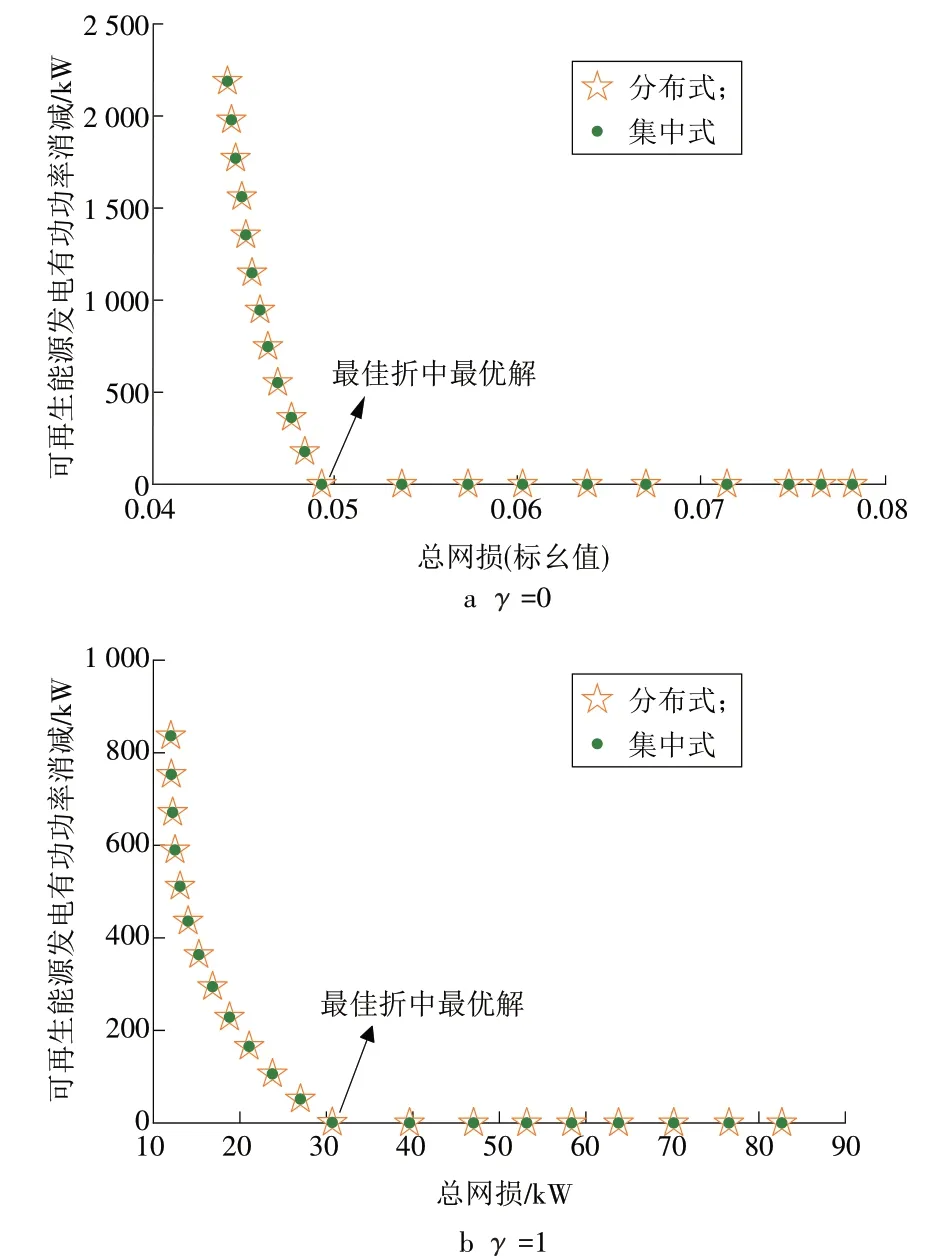
图3 修正的IEEE 33节点配电系统帕累托前沿解集Fig.3 Pareto frontier of the updated IEEE 33-bus distribution system
为了展示所提分布式MO-OPF 算法的电压调节能力,图4 给出了基于以下3 种场景的电压分布。场景1:无优化,分布式电源注入最大可用功率而没有任何缩减;场景2:MO-OPFγ=1;场景3:MO-OPFγ=0。由图4可知,在没有优化的场景1下,节点13-18的电压值超过了1.04(标幺值)的上限,因为反向电流很大,而场景2 和3 所得的电压在限制范围内。值得注意的是,场景2 中的电压幅度有一个非常窄的余量,因此功率的轻微波动都可能触发过电压。在这种情况下,增加电压偏差目标,这种风险可以减轻,如场景3所示。

图4 3种场景下修正的IEEE 33节点配电系统电压分布Fig.4 Voltage distributions of the updated IEEE 33-bus distribution system under three conditions
为了测试所提方法的灵活性,假设在MO-OPFγ=0的情况下,节点12母线(简称PV12)所接的光伏逆变器因故障或通信中断而退出运行。
配电运营商与PV12 所在能源运营商之间的电力交换和通信不再进行。由于PV12 所在能源运营商的辅助等效注入功率变量变为0,导致网络侧PV12 的功率不平衡。功率不平衡首先会引起单目标模型的新迭代,直到收敛到新的最优目标值,需更新MO-OPF 模型的正交约束集。然后,对MOOPF 模型实施新的迭代,直到它收敛到一个新的最佳折中解。注意,轻微的系统扰动对位于帕累托最优边界上的最佳折中点的选择影响很小。因此,只需要为最佳折中点实现新的迭代即可。PV12 所接的光伏逆变器退出运行后系统迭代进程如图5所示。
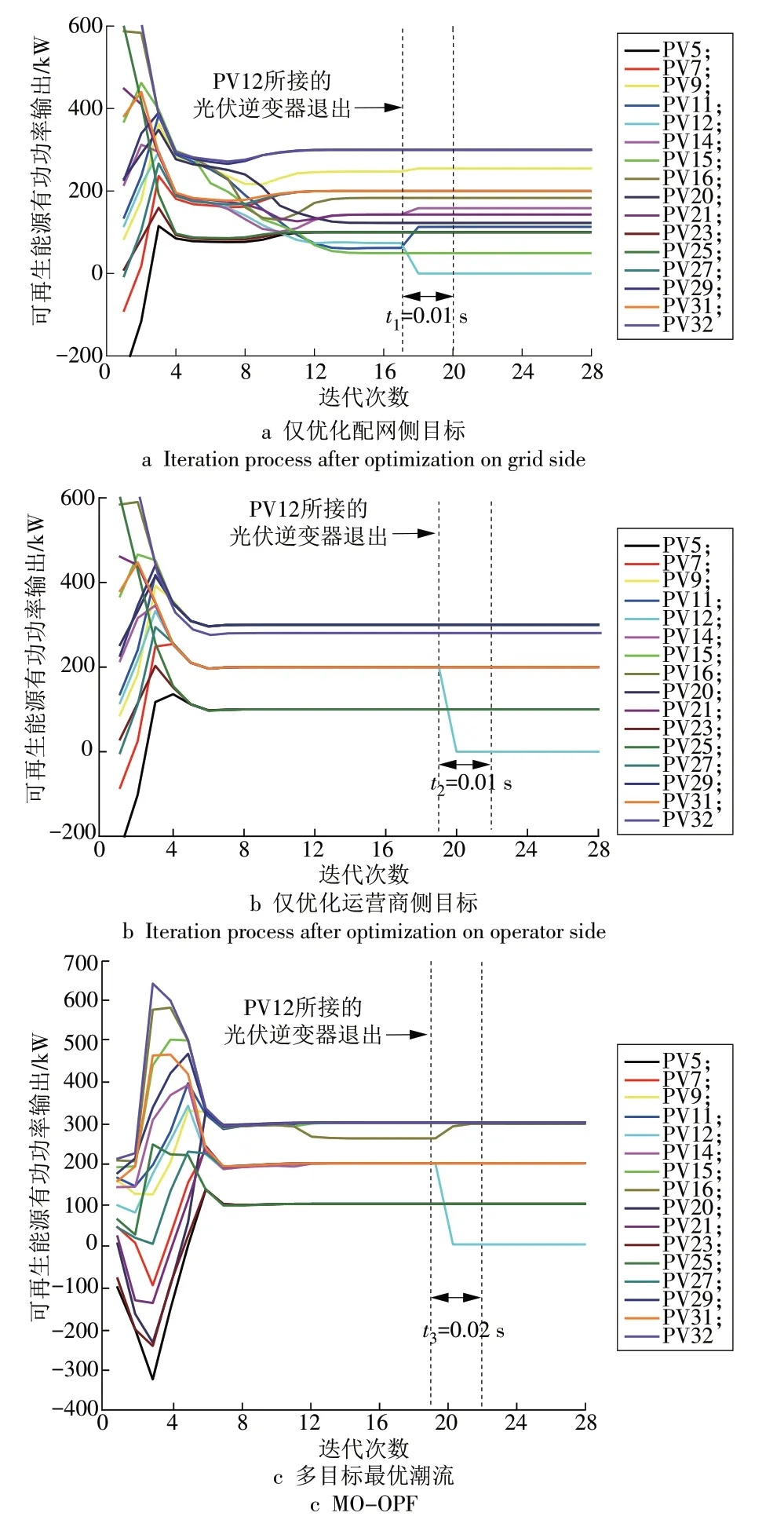
图5 PV12所接光伏逆变器退出运行后系统迭代进程Fig.5 System's iteration process after the decommissioning of the PV inverter connected to bus 12
扰动后,单独优化配网侧或能源运营商侧的目标,系统仅需迭代0.01 s获得新的最优解,折中点也仅需0.02 s可获得收敛的最优解。因此,对PV12所接的光伏逆变器故障的响应恢复时间可估算为max(t1,t2)+t3,即0.03 s。
4 结论
本文针对主动配电系统MO-OPF 问题提出了一种基于增量交换的分散优化算法。将MO-OPF 模型分解为网络侧和能源侧的目标和约束的总和。
用辅助变量增量的二次函数来表示能源侧优化模型对网络侧模型的影响。因此,在网络运营商和能源运营商之间只需要交换辅助变量增量的信息,这样可以避免向网络运营商暴露任何分布式能源的私有信息。仿真结果表明:(1)该算法可以提供与集中式模型相同的均匀分布帕累托最优解;(2)网络运营商和可再生能源运营商可以追求自己的目标,同时确保电压和分支功率在规定的范围内。
