基于图论的区域综合能源服务商交易路径优化
2024-03-13周冠廷徐凯刘建伟鹿百兴张乔陈新
周冠廷,徐凯,刘建伟,鹿百兴,张乔,陈新
(国网山东省电力公司莱州市供电公司,山东 莱州 261400)
0 引言
大量使用化石燃料带来的全球变暖和环境污染等问题,加速了能源消费结构从化石能源为主向清洁能源为主的转变[1-3]。综合能源系统作为能源互联网的物理载体,实现了多能互补和可再生能源的有效利用[4-7]。2017 年年初,国家能源局公布了23 个首批入选多能互补集成优化示范工程项目,国家电网于2017 年和2019 年陆续发布了“关于开展综合能源服务业务的意见”和“2019—2020 年推进综合能源服务业务发展行动计划”,进一步明确了综合能源服务的重点发展任务和目标[8-9]。
随着电力市场体制的建立健全,区域综合能源服务商将会大量出现,为保证电网秩序和市场稳定,电网调度中心对其的管控调度尤为重要。目前,对多区域综合能源服务商的研究主要侧重于综合能源服务的市场模式分析[10-12]、交易及博弈方法[13-16]、可靠性及稳定性评估[17-19]、经济性优化调度[20-23]等。文献[24]基于高比例风电渗透的情况,建立博弈论模型,讨论了电力市场环境下参与者的最优决策行为。文献[25]基于主从博弈,充分考虑能源服务商和用户的双方利益,对区域综合能源服务商的定价策略进行了研究。以上研究多针对单一区域能源服务商和多用户之间。对于多区域能源服务商的研究集中于能源站和管线的规划方法[26-28]。文献[29]在“能距”理论的基础上,建立了综合能源系统站网规划模型,提出了综合能源站选址和管网分布问题。文献[30]基于改进型Kriging模型,对综合能源系统的设备容量配置和运营策略进行规划。但现有文献大多忽略了综合能源站与站之间的协同关系,且针对短时间内不同能源站之间协同合作路径选择问题的研究较少。当多个区域综合能源服务商出现时,网络结构变得复杂,不同服务商电量剩余与不足的情况不同,购、售电双方的交易路径越来越复杂,可选择的路径也越来越多。如何在考虑多方转运和输送线路容量限制的情况下,在电厂、服务商和用户之间以及多服务商之间寻找最优的交易路径,是非常有研究意义的。
本文结合目前我国的电力市场改革方式,以区域综合能源服务商为研究对象,探讨其在市场中的交易路径优化选择问题。首先提出区别于传统交易路径架构方式的区域综合能源服务商交易路径。然后提出两步式交易路径选择模型:第1 步交易路径优化模型,用于区域综合能源服务商的站址规划;第2步交易路径优化模型,用于多个区域能源服务商之间的能源传输路径选择。最后,通过算例仿真验证所提模型的有效性和可行性。
1 区域能源服务商交易概述
1.1 传统交易路径架构
目前,传统的电能交易路径无论是发电厂、可再生能源发电还是能源转换设备,发出的电能都必须经过电网公司统筹安排,不能直接对用户进行售电,因此其交易路径的选择有且只有一条,即发电厂→电网→用户。在传统的电能交易路径方式中,由于电网公司处于垄断地位,地理位置的影响几乎可以被忽略。
1.2 区域能源服务商架构
区域综合能源系统主要由能源供应商、区域能源服务商、用户等3 部分组成,如图1 所示。能源供应商由多个发电厂和天然气厂组成,风光等可再生能源发电,储能装置和能源转换设备(热电联产(CHP)设备、电转气(P2G)设备、燃气锅炉)放电,区域能源服务商可通过日前市场和实时市场从能源供应商处购能,向用户出售电能赚取利润。区域能源服务商是区域综合能源系统的桥梁,通过连接能源供应商和用户,实现能源的协调运行。

图1 区域综合能源系统能量流Fig.1 Energy flows in a regional integrated energy system
区域能源服务商的服务内容包括能源供应服务、能源销售服务和能源效益服务。其中能源供应服务是充分利用园区能源设备,运营配电网,构建多能互补的能源服务平台;能源销售服务主要是能源销售;能源效益服务主要包括辅助服务等。本文着重考虑区域能源服务中的电能交易路径问题以及电能相关利润,气、热能相关利润可采用“以电定热”和“以电定气”的方法确定,本文不再赘述。
区域能源服务商的运营系统结构如图2所示。
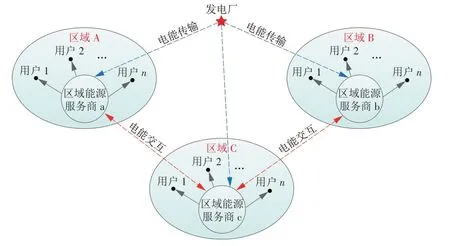
图2 区域能源服务商运营系统结构Fig.2 Structure of a regional integrated energy service provider
区域能源服务商参与下的电能交易路径区别于传统的交易路径,其特点如下。
(1)电能传输路径不再单一。电能可以从发电厂到电网再到用户,也可以从发电厂到区域能源服务商再到用户,或直接从区域能源服务商到用户。
(2)各区域能源服务商可以实现电能交互、互通,最大限度减少电能浪费并降低弃风弃光量。
(3)区域能源服务商的覆盖范围有限。电能的传输需要考虑线路容量限制、变压器容量限制、电力系统稳定等方面的影响;同时,由于多次转运而产生网络损耗会提高输配电成本。
2 区域能源服务商交易路径数学模型
2.1 第1步交易路径选择模型
在常见的选址问题中,受地理环境、辐射范围和投入成本等多方面因素的影响,待选对象常有一个或多个可选位置,在这些位置进行建设会使待选址对象的综合效益最佳。p-中位模型目前广泛应用于选址问题的研究中,即如何在可选范围内为p个待选址对象选择最优位置。本文提出改进的p-中位模型是在传统的p-中位模型引入0 —1 变量,用于考虑待选址对象的建设成本。该模型具体可描述为:在一个记为G=(V,E,W)的无向图中(其中:V为所有顶点的集合;E为所有边的集合;W为所有边的权重集合),从顶点集合中寻找一子集合Vv,该集合中的顶点称为中位点,使除Vv之外的顶点集合{V-Vv}到Vv中最近顶点的距离和最小。p-中位模型的数学表达式为
式中:M为需求点集合;N为候选点集合;ai为第i个需求点的需求量;dij为第i个需求点到第j个候选点的最短距离;xj表示第j个候选点是否被选中,被选中为1,否则为0;yij表示第j个候选点是否为第i个需求点提供服务,提供为1,否则为0。
第1步采用改进的p-中位模型确定区域综合能源服务商的位置。从候选的能源站地址中选出p个位置,使得区域综合能源服务商的综合建设运行成本最小、能源站与负荷中心的最短路径距离与用户负荷需求之积最小。
式中:CRIES为区域综合能源服务商的综合建设运行成本;xi表示第i个侯选位置是否建设能源站,建设为1,不建设则为0;Pu为第u个用户聚合点的负荷需求;dui为第u个用户聚合点到第i个区域综合能源服务商之间的最短距离;yui表示第i个侯选位置是否为第u个用户聚合点提供服务,提供服务为1,否则为0;I为区域综合能源服务商数量;U为用户聚合点数量。
区域综合能源服务商的综合建设运行成本主要包括综合能源站的投资、维护成本和综合能源管网成本。
式中:Cst为综合能源站投资、维护成本;Cpi为综合能源管网成本。
式中:Cinv为区域综合能源服务商的初始投资成本;Cmt为区域综合能源服务商运行t年所需的维护成本;r为区域综合能源服务商综合折旧率;ti为区域综合能源服务商i的运行时间;αi为区域综合能源服务商i的投资费用系数;c0为区域综合能源服务商单位容量所需的投资成本;Pi为区域综合能源服务商i的容量;cmt为区域综合能源服务商单位容量所需的维护成本。
式中:N为新建的区域综合能源系统所需管网数量;cn,p为管网n单位长度的费用;ln为管网n的长度;rp为管网折旧率;ψ为管网寿命;cn,b为管网n的建设成本;cn,loss为管网n的运行损失成本;cn,pmt为管网n的运行维护成本;λ为管网保温材料系数;tc为管网正常工作时的内外平均温差;tP为循环水泵的年最大工作时间;pe为电价;dn为管网n的直径;δn为管网n的厚度;δtn为管网n的保温层厚度;COP为区域综合能源服务商的能效比;μ为管网维护成本系数。
约束条件如下。
(1)节点平衡约束。区域综合能源服务商从发电厂购买的电量与其自身产出的电量之和等于对用户的售电量,即
式中:Pgi为区域综合能源服务商i从发电厂g购买的电量;Piu为区域综合能源服务商i向用户聚合点u出售的电量;为备用上调量,即区域综合能源服务商放出的电能;为备用下调量,即区域综合能源服务商吸收的电能;G为发电厂数量。
针对拓扑网络图中的节点,节点i注入的有功功率和无功功率分别为
式中:Vi为节点i的电压;Gij为支路i—j的电导;Bij为支路i—j的电纳;θij为节点i和节点j之间的电压相角差。
(2)供应能力最大约束。区域综合能源服务商i从发电厂g购买的总电量不超过发电厂g的最大供应能力,即
区域综合能源服务商i向用户聚合点u的售电量不小于用户聚合点u最小用电量且不超过服务站本身最大容量,即
(3)线路功率传输限制约束。线路g-i和线路i-u上传输的电量分别不超过其最大传输电量,即
(4)区域综合能源服务商数量约束。开放的区域综合能源服务商数量不超过允许的最大数量,即
式中:Imax为区域综合能源服务商允许开放的最大数量。
2.2 第2步交易路径选择模型
传统的OD 矩阵是指将所有交通区域按照起始点(Origin)和目的地(Destination)进行排序,以任意2 个区域的交通流量为元素的矩阵[31]。本文在此基础上进行改进,设t时刻j1区域综合能源服务商的电能供应量为Pj1,j2区域综合能源服务商的电能需求量为Pj2。记从j1区域综合能源服务商到j2区域综合能源服务商的电能传输量为Pj1j2,由Pj1j2构成的矩阵即为OD 矩阵,其第j1行元素表示从第j1个区域综合能源服务商输送给其他各区域综合能源服务商的电量,第j2列元素表示各个区域综合能源服务商输送给第j2个区域综合能源服务商的电量。
本文引入双约束重力模型对OD 矩阵进行处理。从区域综合能源服务商j1到区域综合能源服务商j2的电能传输量Pj1j2可以看作是2 个区域综合能源服务商之间的某种吸引程度,可以用2 个物体的引力来比拟。区域综合能源服务商j1在t时刻的电能剩余量越大,区域综合能源服务商j2在t时刻的电能需求量越大,那么通常从j1输送给j2的电量也越大,j1电能的剩余量和j2对电能的需求量可以用2 个物体的质量进行比拟。两者间传输的电量受距离、网损、电价等因素的影响,统称为阻抗因素,记为Rj1j2。
双约束重力模型为
式中:aj1,bj2均为平衡因子;f(Rj1j2)为区域综合能源服务商j1和j2之间的阻抗函数。
为简化模型,取f(Rj1j2)的幂指数形式,且其幂指数为1,即f(Rj1j2) =Rj1j2。
由此可以写出OD矩阵为
对OD矩阵进行概率转移处理,即
各区域综合能源服务商之间的电量转移关系迭代公式为
该迭代式表示,在经过第k+1步的迭代之后,第k+1 轮各区域综合能源服务商的转移电量为第k轮各区域综合能源服务商的转移电量经过概率转移矩阵变化后的值。
交易路径第2步优化选择模型以电能传输量最大和区域综合能源服务商日运营利润最大为目标函数。
式中:It为区域综合能源服务商的日运营利润;为区域综合能源服务商实时购售电利润;为区域综合能源服务商实时网络损耗成本。
式中:pjnk,t为t时刻区域综合能源服务商jn向k用户的售电价格;Pjnk,t为t时刻区域综合能源服务商jn向k用户的售电量;pijn,t为t时刻区域综合能源服务商jn向i发电厂的购电价格;Pijn,t为t时刻区域综合能源服务商jn向i发电厂的购电量;pjn,t为t时刻区域综合能源服务商jn向其他服务商的购售电价格;Pjn,t为t时刻区域综合能源服务商jn向其他服务商的购售电量,正值表示购电,负值表示售电。
文中考虑如下约束条件。
(1)节点平衡约束。t时刻区域能源服务商jn从发电厂购买电量、自身产出电量和与其他区域能源服务商互补电量之和等于输送给用户的电量。
(2)线路最大容量约束。t时刻区域综合能源服务商之间的线路jn—jm传输的电量不超过其最大传输电量,即
(3)传输功率限制约束。t时刻线路从区域综合能源服务商jn到jm的电能传输量不超过区域综合能源服务商jn的剩余电量,若无剩余电量,则其电能传输量为0。
2.3 基于枚举法和Dijkstra算法的求解方法
对于第1 步交易路径选择模型,目前常采用枚举法或遗传算法、蚁群算法等启发式算法对p-中位问题进行求解。枚举法只能用于求解较小规模问题,但能获得最优解。启发式算法可以广泛应用于较大规模问题的求解,但不同算法存在各自的局限性:贪婪算法可能会使最终结果陷入局部最优而非全局最优;蚁群算法对优化问题的初始参数要求较高;遗传算法的局部搜索能力有所欠缺。本文将局部搜索算法与图论中的最短路径Dijkstra 算法相结合,提出了一种求解p-中位问题的方法。该方法不仅减少了计算量,缩短了计算时间,而且便于求解较大规模问题。
在一个记为G=(V,E,W)的区域综合能源服务商网络图中,根据图中各顶点的关联情况,可以写出边矩阵E,具体如下。
式中:e(i,j) ∈E;i,j∈V。
然后根据边矩阵E及网络图中的信息,求解权重矩阵W,具体如下。
式中:wij∈W;Cij,p为顶点i和顶点j间的管网成本。
采用图论中最短路径Dijkstra 算法求解网络中各顶点的最小权重,权重矩阵D的计算方式如下。
式中:dij∈D,表示顶点i和j间的最小权重。
记l(i,j)为顶点i和j取最小权重时两者间的路径,由l(i,j)构成的矩阵为路径矩阵L。
算法具体流程如图3所示。
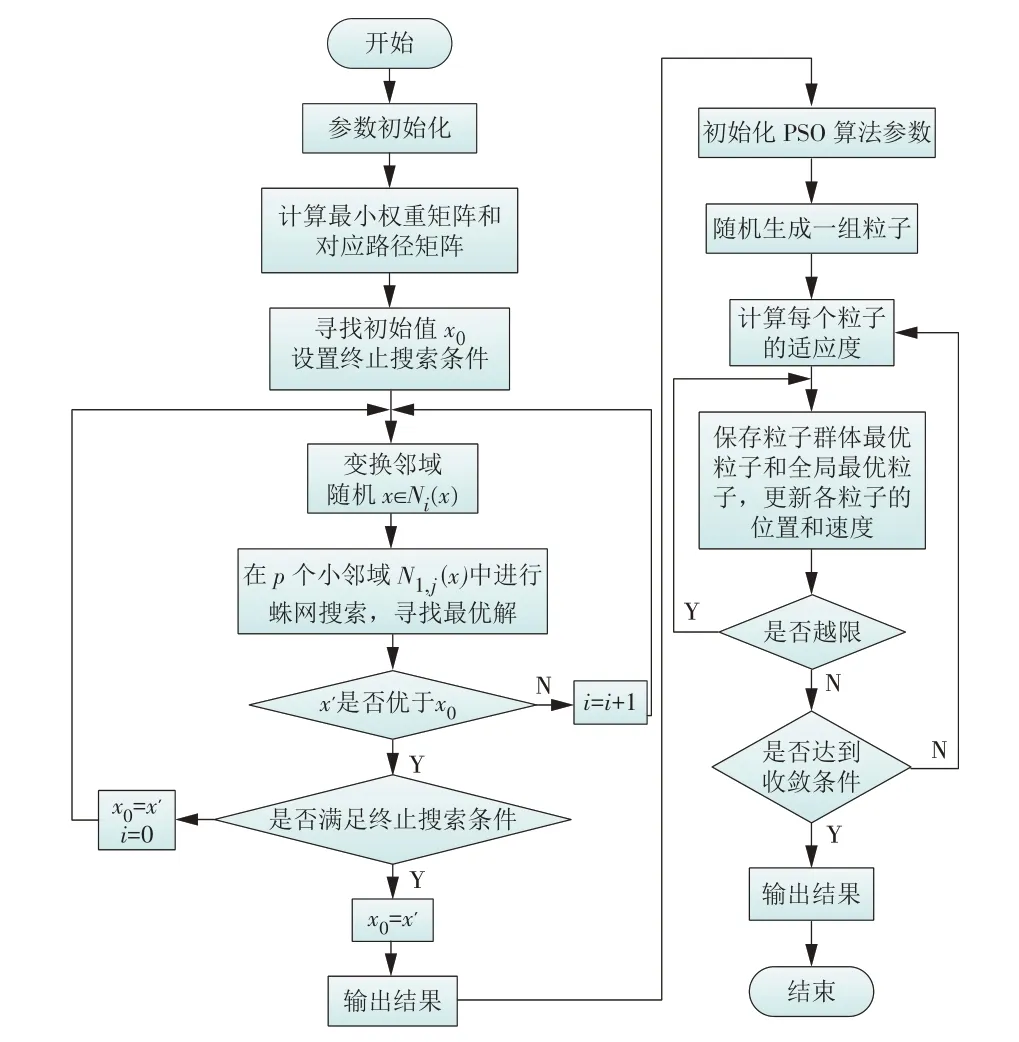
图3 算法流程Fig.3 Algorithm flowchart
(1)利用图论中最短路径Dijkstra算法计算最小权重矩阵和对应的路径矩阵。
(2)利用贪婪算法,先寻找初始解x0,然后设置终止搜索的条件。
(3)对邻域进行变换,对邻域N1(x)进行划分,对划分后的小邻域N1,j(x)进行蛛网搜索,得到局部的最优解x'。
(4)将局部最优解x'与初始解x0进行比较。若在满足终止搜索条件的前提下,局部最优解x'更优,则计算结束,输出结果;若局部最优解x'更优,但不满足终止搜索条件,则令x0=x',i=0,返回(3);若初始解x0更优,则i=i+1,返回(3)。
采用粒子群优化(Particle Swarm Optimization,PSO)算法对第2 步交易路径选择模型进行求解,具体算法流程不再赘述。
3 算例仿真
3.1 基础参数设定
算例设置一个100 km×100 km 的虚拟地图,发电厂数量为2,区域能源服务商最大数量为6,随机设置20 个用户聚合点,具体位置如图4 所示。假设发电厂、区域能源服务商及各用户聚合点间均存在输电线路,其电气距离近似等于其直线距离,所有输电线路的单位电阻均为0.2 Ω/km,发电厂与区域能源服务商之间的输电线路电压均为220 kV,区域能源服务商与用户之间的输电线路电压均为12.66 kV,各区域能源服务商之间的输电线路电压为110 kV。在该虚拟地图中,假设用户聚合点距中心点越远用电量越少,但外围存在可从发电厂直接购电的大用户p,q,s。不同区域能源服务商向发电厂购电价格与向用户的售电价格见表1,区域能源服务商之间的互补电价均为0.2 元/(kW·h)。

表1 区域能源服务商购售电价格Table 1 Electricity purchasing and selling price of regional energy service providers元/(kW·h)

图4 虚拟地图分布Fig.4 Distribution on the virtual map
3.2 仿真结果分析
对于中长期负荷预测,采用某地区近5 年的电力负荷数据和区域能源服务商自产电能数据为训练样本,然后采用基于改进的BP神经网络算法分别建立负荷预测模型和区域能源服务商自产电能预测模型。区域能源服务商自产电量预测见表2,中长期用户负荷预测如图5所示。

表2 区域能源服务商自产电量预测Table 2 Forecast on electric energy generated by regional energy service providersMW·h
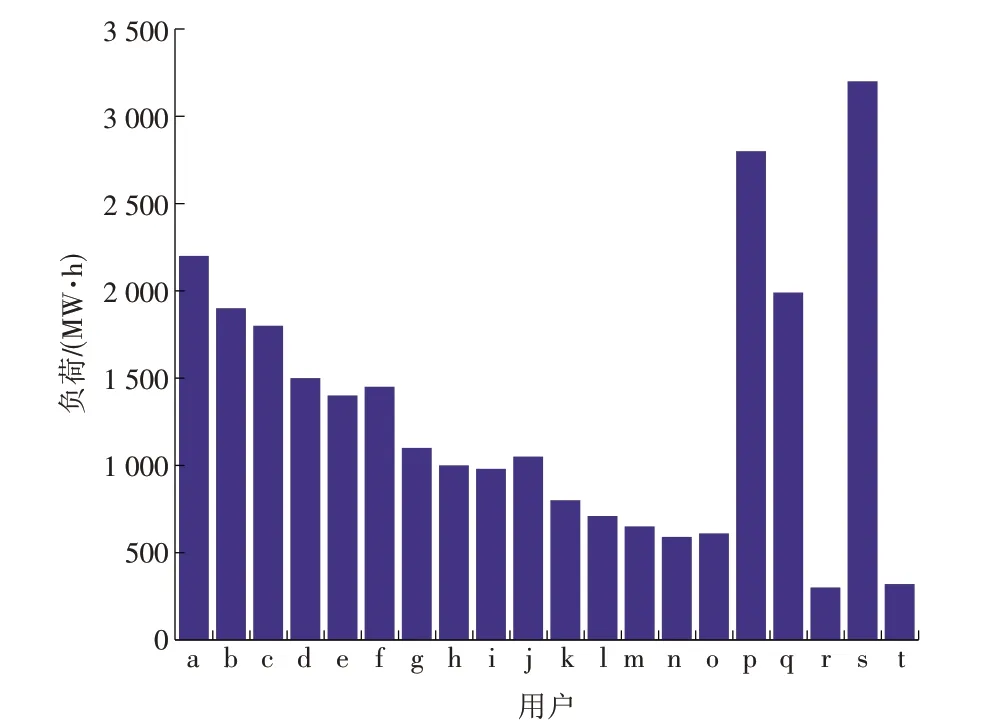
图5 中长期用户负荷预测Fig.5 Medium and long-term forecast on users' loads
根据本文提出的基于网络流的第1步交易路径选择模型,计算结果如图6所示。
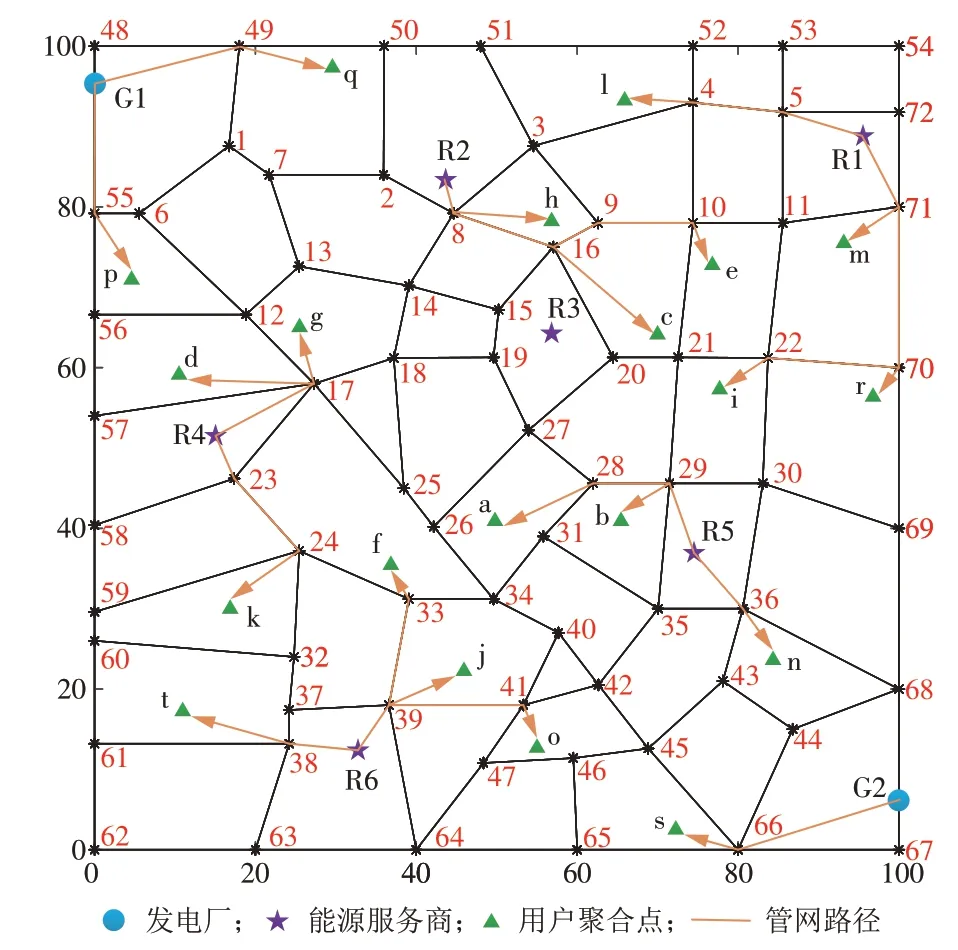
图6 第1步交易路径选择结果Fig.6 Transaction path after the first-step optimization selection
在6 个候选区域能源服务商中,选择R1,R2,R4,R5,R6 等5 个服务商分别负责相应的用户。其中大用户p和q直接从发电厂G1直接购电,大用户s直接从发电厂G2 直接购电;用户聚合点l,m,i 和r由能源服务商R1 供能;用户聚合点c,e 和h 由能源服务商R2 供能;用户聚合点d,g 和k 由能源服务商R4 供能;用户聚合点a,b 和n 由能源服务商R5 供能;用户聚合点f,j,o和t由能源服务商R6供能。区域能源服务商的运营利润及损耗见表3。

表3 区域能源服务商运营利润及损耗Table 3 Profits and expenses of regional energy service providers万元
当采用传统交易路径时,由于路径单一,电能传输路径变长,网络损耗增加。在用户用电功率不变的情况下,网络损耗为42.13万元,相比基于网络流的区域能源服务商第1步交易路径优化选择模型优化后的总损耗成本增加69.31%。证明本文提出的第1 步交易路径模型可以有效降低网络损耗成本。
在区域能源服务商第1步交易路径选择模型优化的基础上,采用某地区近7 d 的电力负荷数据和区域能源服务商自产电能数据作为训练样本进行预测。其预测值用于区域能源服务商第2步交易路径选择。区域能源服务商自产电能及用户用电量的实际值与预测值差的和记为负荷差,如图7所示。

图7 区域能源服务商负荷差Fig.7 Load gaps of regional energy service providers
负荷差会导致区域能源服务商弃风弃光,采用前文提到的基于OD 矩阵的第2 步交易路径优化选择模型进行处理后,其结果如图8所示。

图8 优化前后区域能源服务商弃电量对比Fig.8 Abandoned electricity of regional energy service providers before and after the optimization
经过基于OD 矩阵的区域能源服务商第2 步交易路径优化后,各服务商之间可以实时进行电能传输,有剩余电量的服务商释放剩余电量,电量不足的服务商优先从其他服务商处购入电量,从而最大限度减少弃风弃光量,提高区域能源服务商的运营利润。区域能源服务商运营利润对比如图9 所示。由图9可见,采用基于OD矩阵的区域能源服务商交易路径第2 步优化选择后,区域能源服务商运营利润提高,弃电量明显降低。

图9 区域能源服务商运营利润对比Fig.9 Operating profits of different regional energy service providers
图8—9证明了本文提出的基于OD矩阵的区域能源服务商第2步交易路径选择模型可以在减少区域能源服务商弃风弃光量的同时,提高区域能源服务商的运营利润。
为验证本文所提算法的有效性和先进性,采用枚举法和遗传算法分别进行求解过程对比。通过Matlab 仿真,当采用枚举法和Dijkstra 算法结合的方法时,计算机运行时间为90 s左右,而仅采用枚举法时,运行时间为120 s左右,且计算次数高于结合法;采用遗传算法时,计算机运行时间为60 s左右,但经常会陷入局部最优并对初值要求较高。综上所述,采用枚举法与Dijkstra算法结合进行求解,能够在考虑所有可行解的基础上,减少计算次数,降低初值对计算的影响。
4 结论
本文提出了基于图论的区域综合能源服务商交易路径优化方法。首先基于改进的p-中位模型建立第1 步交易路径选择模型,充分考虑了综合能源站的综合建设运行成本和建设成本,以综合建设运行成本、能源站与负荷中心的最短路径距离与用户负荷需求之积最小为目标函数,解决区域综合能源服务商的选址规划问题。然后以OD 矩阵和重力模型为基础,以电能传输量最大和区域能源服务商日运营利润最大为目标函数,解决多区域能源服务商之间能源互补传递路径选择问题。最后通过仿真验证,证明了本文所建模型的有效性和可行性。
