核主泵机械密封可靠性Bayes分析的适应性
2024-03-13高灯孙见君张玉言
高灯,孙见君,张玉言
(南京林业大学机械电子工程学院,江苏南京 210037)
核主泵利用流体动压型机械密封防止反应堆内含放射性、高温或高压冷却流体的泄漏,其可靠性对核电站的安全稳定运行具有举足轻重的作用[1]。为了确保系统安全、稳定、可靠运行,运行商常定期更换在役机械密封件,并记录下这些未失效机械密封的相关数据。如何利用无失效数据去估计核主泵机械密封可靠性一直为工程技术人员所关注。
无失效数据研究可以追溯到1979年MARTZ和WALLER[2]的研究。大多数无失效数据研究主要集中在置信限法和结合先验信息的Bayes类方法上,面向航天发动机、船舶、电子元器件、轴承等高可靠性要求产品。韩明、沈继红、宋永刚等[3-5]结合Bayes理论探讨了产品寿命服从指数分布的可靠性评估方法。SONG和CAO[6]给出了先验分布为Gamma分布结合Bayes模型的失效概率标准平方误差损失函数。JIANG等[7]将函数凹凸性和Bayes理论相结合,给出了Weibull分布下,失效概率区间的估计值。金光和沈静[8]针对小样本无失效卫星活动部件可靠性评估问题,提出一种Bayes信息融合技术,充分利用不同型号相似活动部件数据,来提高评估精度。高攀东、蔡忠义、姜祥周等[9-11]探讨了E-Bayes估计与多层Bayes估计应用在其他高可靠性产品的优劣性。傅惠民等[12]提出一种可靠性评估和寿命预测的方法,旨在提高寿命实验中出现极少失效数据场合下的预测精度。该方法缺陷在于需知道Weibull分布形状参数的下限。贾祥等人[13]给出了产品服从Weibull分布的一般可靠性分析步骤。
上述研究为Bayes类方法拓展至重要装备的机械密封可靠性评估提供了有益借鉴。肖丽丽等[14-15]针对核主泵机械密封可靠度评定问题,通过最优置信限法估计可靠性参数,并探讨了影响参数估计值的主要因素;之后基于配分布曲线法和修正似然函数法分析了参数估计值和给定时间的可靠度估计值,并指出了2种方法的不同适用范围。置信限法得出的结果往往较为“保守”,不够精确,而Bayes类方法可以有效弥补置信限的“保守”问题,但却因先验信息的不同而有差别,从而影响了可靠度评估的精度。可见,Bayes理论应用于核主泵机械密封可靠度评估仍需更多的探讨。
本文作者拟通过搜集到的大亚湾核主泵机械密封的故障数据,确定其可靠度分布;结合配分布曲线法建立基于Bayes理论的核主泵机械密封可靠性评估模型;最后,通过故障数据确定的可靠度分布参数做无失效仿真算例,探究先验分布参数对E-Bayes估计和多层Bayes估计精度的影响。研究成果可为进一步开展基于Bayes理论的核主泵机械密封可靠性评估工作奠定基础。
1 大亚湾核主泵机械密封小样本数据可靠度分布的确定
为确定搜集到的大亚湾核主泵机械密封故障数据所服从的寿命分布类型,文中分别采用常见的指数分布和Weibull分布对数据进行拟合,通过拟合优度确定寿命分布类型,从而为后续基于无失效数据核主泵机械密封可靠度评估提供一个参照。
1.1 数据来源
搜集到的核主泵机械密封数据来源于文献[16],保留故障退出的数据,去除正常退出的情况,筛选得到核主泵机械密封的寿命数据,见表1。
1.2 可靠度分布的确定
图估计法是工程上常用的直观易懂、简单易行的方法,该方法适用于样本容量不大的场合。当样本数量为n时,通过可靠性试验可以得到n个故障时间,然后将故障时间按照依次增加的顺序排列为t1,t2,…,tn。当样本容量有限时,对应的各故障时刻的累积分布F(ti)可由公式(1)[17]近似计算。
(1)
由式(1)可以计算得到n个数据对,即(t1,F(t1)),(t2,F(t2)),…,(tn,F(tn))。 当通过线性化处理,使累积故障概率F(ti)与t具有直接或者间接的线性关系时,可初步认为寿命数据来源于这种分布。累计失效概率见表2。
(1)指数分布拟合
当产品的寿命时间满足指数分布时,对指数分布函数F(t)=1-e-λt进行线性变化,可以得到:
(2)
设Y=ln(1/(1-F(t))),X=t,则Y和X呈线性关系,λ是斜率。Y和F(t)一一对应的关系拟合结果如图1所示。
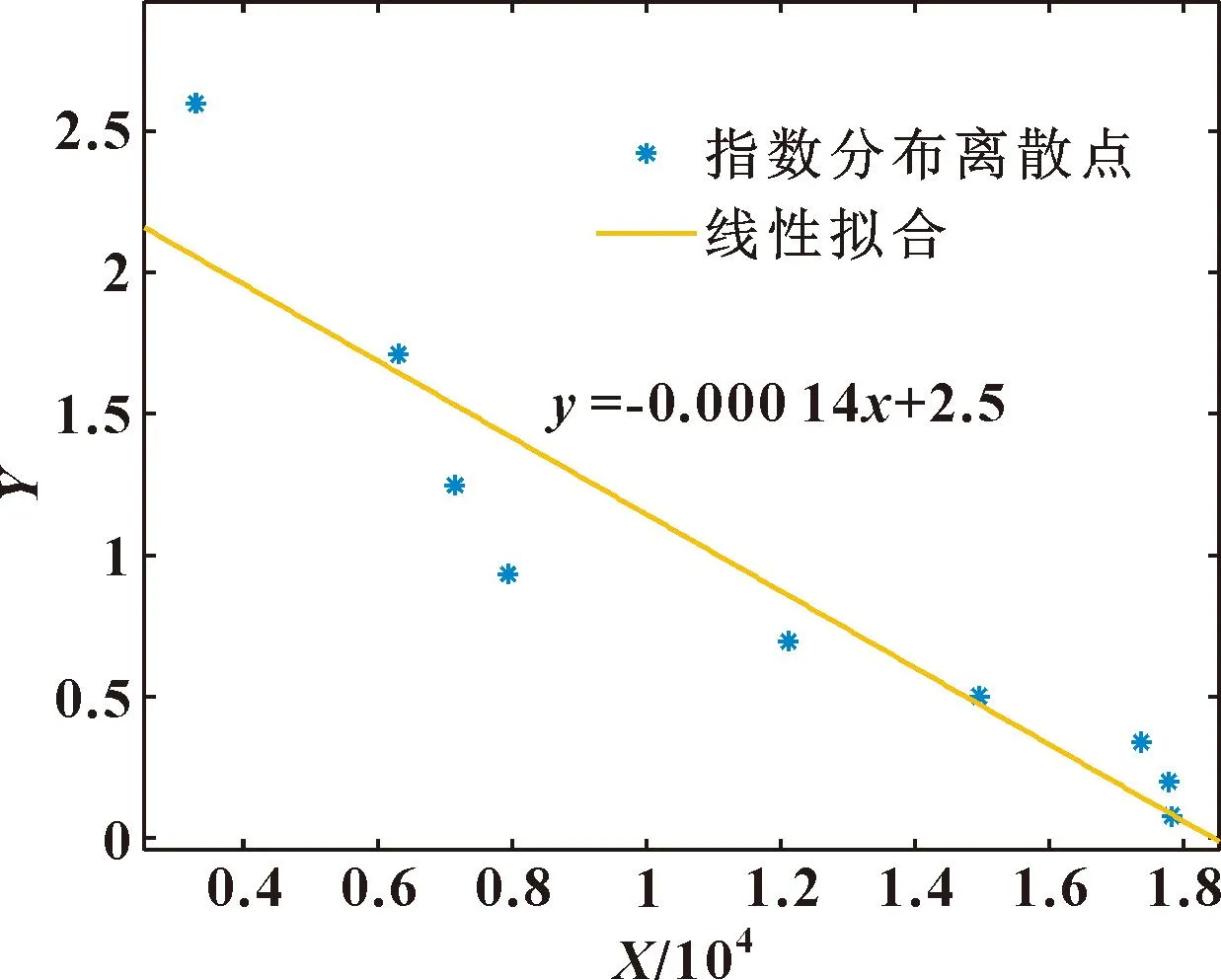
图1 指数分布拟合Fig.1 Exponential distribution fitting
由拟合的直线可知,λ=-0.000 14。拟合结果:F(t)=1-e0.000 14t。
(2)Weibull分布拟合
当产品的寿命时间满足Weibull分布时,对Weibull分布函数F(t)=1-exp{-(t/η)m}进行线性变化,m为形状参数,表征瞬时失效率随时间的变化率,η为尺度参数,表征失效速率的变化快慢,将Weibull分布函数进行变形,可以得到:ln ln{1/[1-F(t)]}=mlnt-mlnη,设Y=ln{ln{1/[1-F(t)]}},X=lnt,则Y和X呈线性关系,直线的斜率为m,此时轴上的截距为lnη。拟合结果如图2所示。

图2 Weibull分布拟合Fig.2 Weibull distribution fitting
拟合结果:
F(t)=1-exp(-(t/12 632)1.8)
(3)
(3)拟合优度比较
求出直线回归方程后,用拟合优度K2作为衡量匹配后直线效果好坏的标准。K2越接近1(或越大),则表明所匹配的直线效果越好。拟合优度结果见表3。
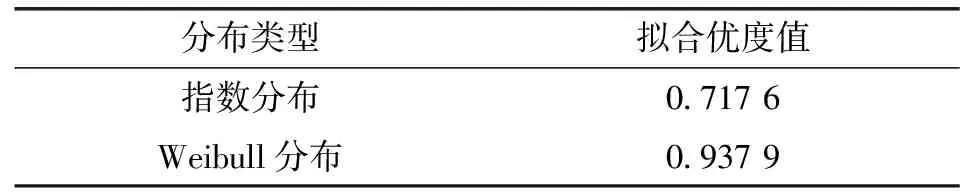
表3 拟合优度计算对比
比较结果可知,Weibull分布拟合效果最佳。所以认为大亚湾核主泵机械密封可靠度服从Weibull分布,把该分布当作基准(见式(4))。
R(t)=exp[-(t/12 632)1.8]
(4)
2 基于配分布曲线法的核主泵机械密封可靠性分析

2.1 先验分布为Beta分布的Bayes方法
Bayes方法中先验分布所含未知参数确定困难时,通过引用先验分布的参数作为超参数,对超参数再给出一个先验,最后综合信息得到可靠性参数的Bayes估计。当试验中机械密封并无失效,且需满足在(0,ti)内机械密封失效概率较小的可能性大,较大的可能性小,此时可选Beta分布作为失效概率pi的共轭先验分布。根据Bayes理论,pi的先验概率密度[17]为
(5)
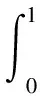
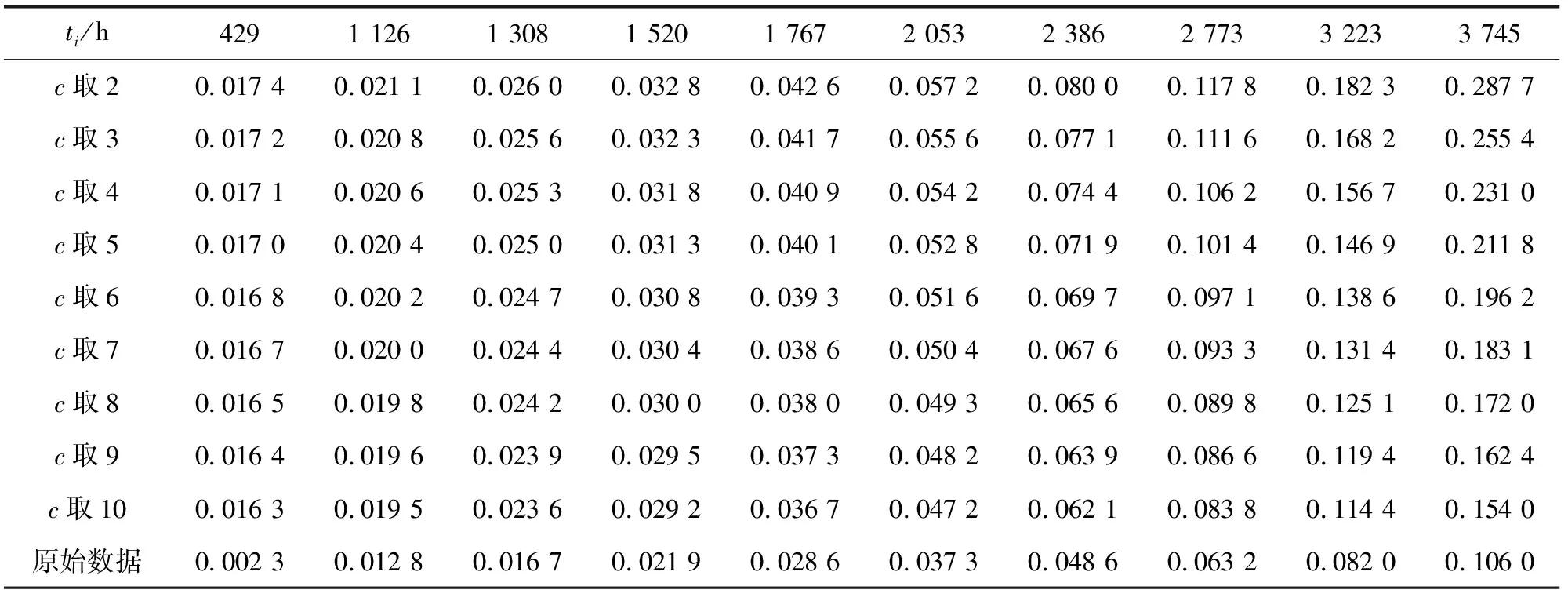
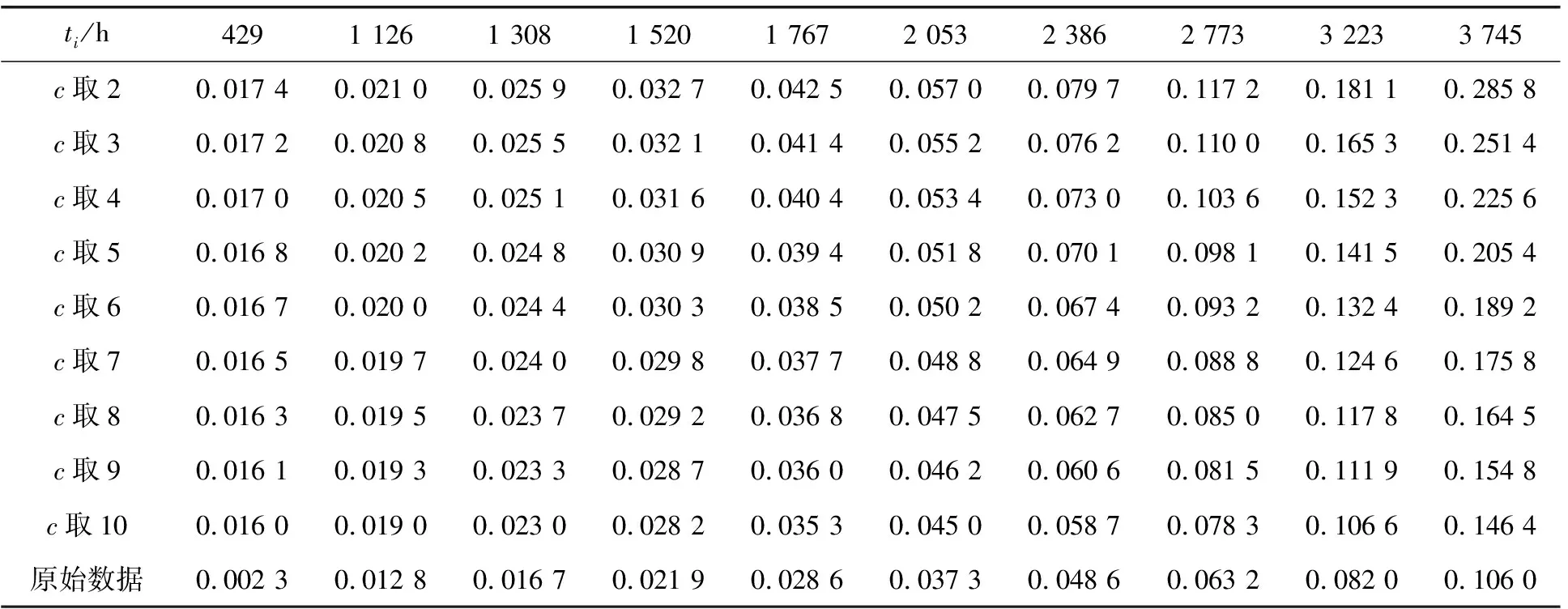
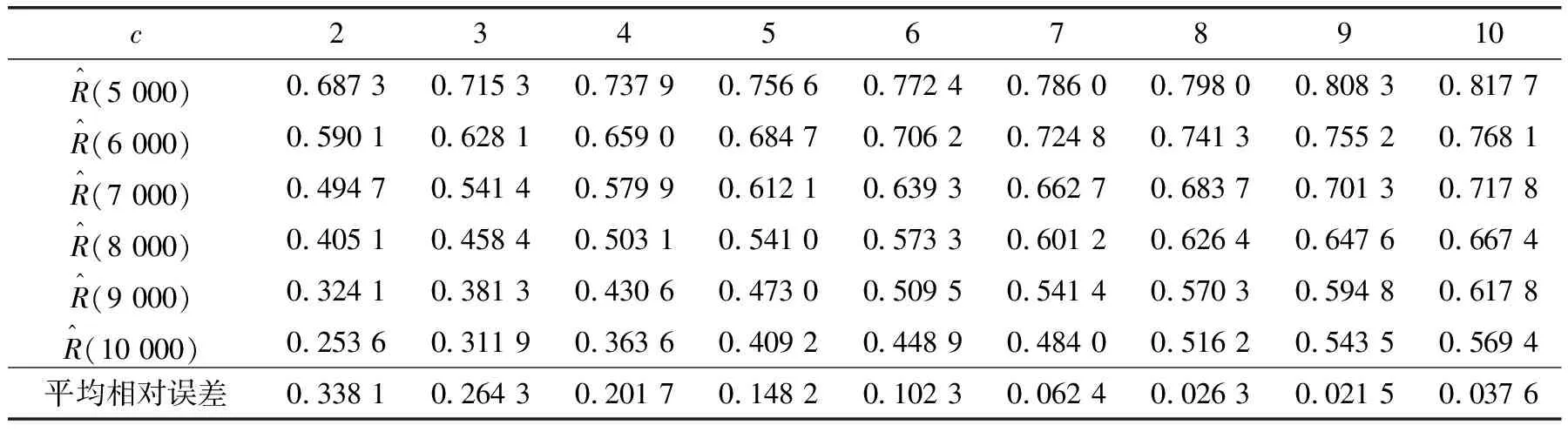
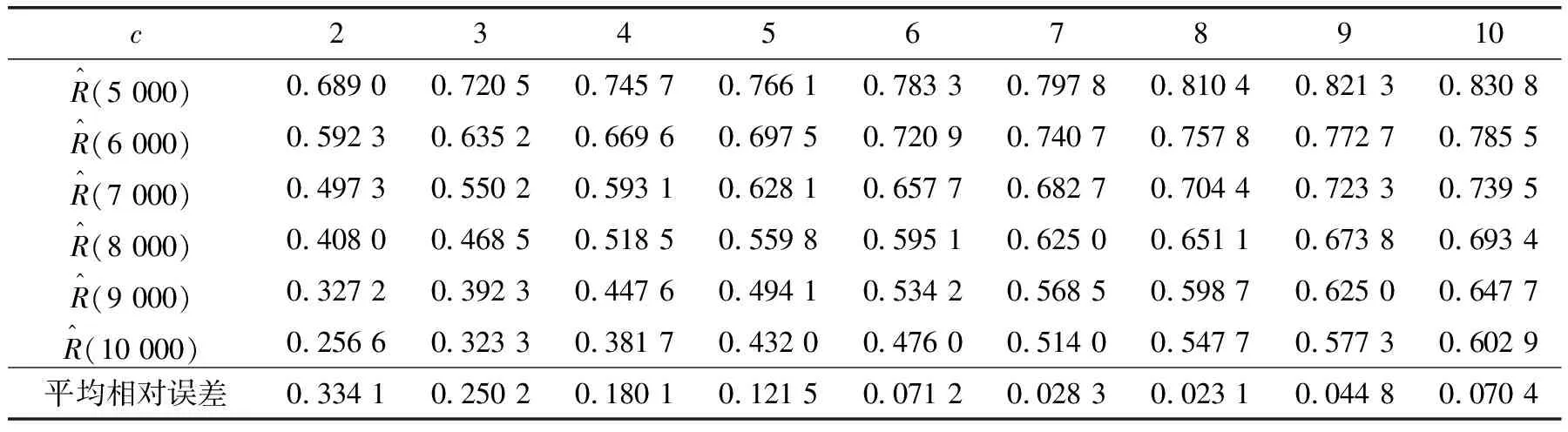
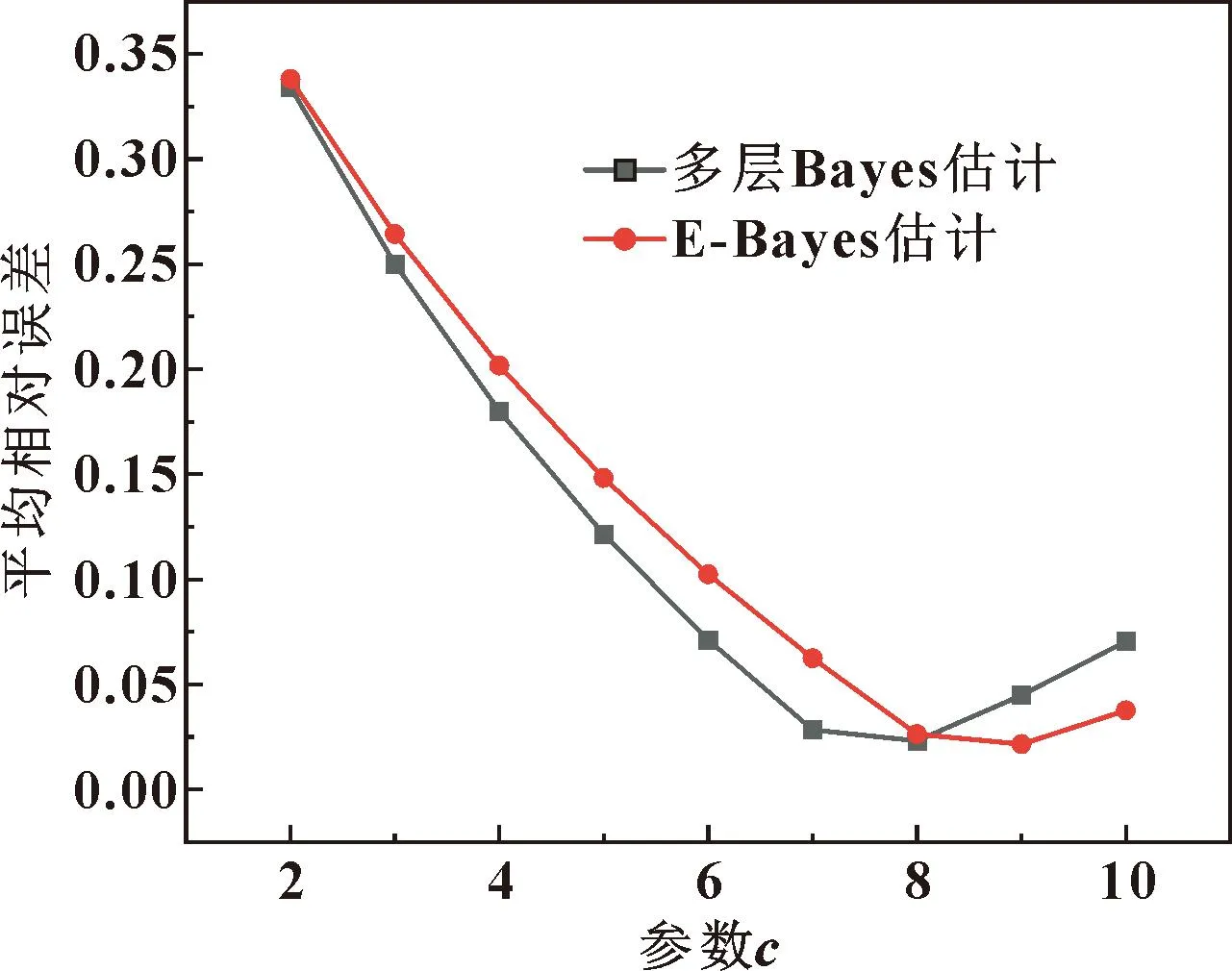
a,b取不同值时,Beta分布有很大区别,b越大,Beta分布概率密度函数尾部越细,Bayes估计的稳健性越差;当0 分别选取超参数a、b在定义域上的均匀分布作为其先验分布[17]: (6) 根据Bayes理论,得pi的多层先验分布[19]为 (7) 2.2.1pi的E-Bayes估计 π(pi|b)=b(1-pi)b-1,0 (8) 又超参数b为先验分布在区间(1,c)上的均匀分布,则在平方损失下,pi的E-Bayes估计[18]为 (9) 2.2.2pi多层Bayes估计 同样,pi的先验由式(8)给出,超参数b的先验分布取区间(1,c)上的均匀分布,则pi的多层先验密度函数[20]为 (10) 由似然函数和先验概率密度函数,可得平方损失下,pi的多层Bayes估计[20]为 (11) (12) (13) 由此不难得到: (14) (15) 最终可求得时刻τ处的可靠度估计: (16) 为比较E-Bayes方法和多层Bayes方法的优劣,以大亚湾核主泵机械密封可靠度函数为基准,通过将2种方法估计出的可靠度与原始可靠度的平均相对误差来比较优劣。表4给出了6个任务时间(h)的原始可靠度。 表4 原始参数下的可靠度 为了讨论c对E-Bayes方法和多层Bayes方法评估精度的影响,运用Monte Carlo法生成服从Weibull分布的随机数,产生该组数据的原始数据为m=1.8,η=12 632,得到一组无失效数据如表5所示。 表5 仿真核主泵机械密封无失效数据样本 表6、表7给出了E-Bayes方法和多层Bayes方法在不同参数c和不同任务时间下的失效概率。数据表明:c一定时,失效概率随时间的增加而增加;时间一定时,失效概率随c的增加而降低。 表6 E-Bayes方法的失效概率估计值 表7 多层Bayes法失效概率估计值 图4 不同参数c下的尺度参数估计值Fig.4 Estimated values of scale parameters under different parameters c 表8、表9给出了E-Bayes估计和多层Bayes估计的平均相对误差。结果表明:时间一定时,可靠度随c值的增加而增加;c值一定时,可靠度随时间的增加而降低。E-Bayes估计平均相对误差达到最低时,c=9;多层Bayes估计平均相对误差达到最低时,c=8。 表8 E-Bayes估计的平均相对误差 表9 多层Bayes估计的平均相对误差 图5示出了E-Bayes估计和多层Bayes估计的平均相对误差随参数c的变化曲线。结果表明:参数c=8时,E-Bayes估计和多层Bayes估计产生的平均相对误差最为接近且均达到较低水平。由此可以推断:针对核主泵机械密封,先验分布为Beta分布时,参数c=8时,评估精度达到最佳水平。 图5 平均相对误差随参数c的变化Fig.5 Variation of average relative error with parameter c (1)建立了结合Bayes理论的可靠性分析模型,并通过大亚湾核主泵机械密封运行数据,验证了c取值适当时结合Bayes理论可靠性分析方法的可行性。 (2)建立的可靠性分析方法的分析步骤:首先通过定时截尾试验获得产品的无失效数据,其次根据Bayes理论计算得到产品失效概率的估计值,最后利用加权最小二乘法拟合离散的失效概率点得出参数的点估计,进而得到可靠度估计。 (3)从E-Bayes估计和多层Bayes估计所产生的平均相对误差来看,c<8时,优先选择多层Bayes估计;c>8时,优先选择E-Bayes估计。 (4)针对无失效情形下核主泵机械密封的可靠性分析问题,先验分布为Beta分布时,参数c=8时,E-Bayes估计和多层Bayes估计所产生的误差均达到较低水平。2.2 失效概率估计方法
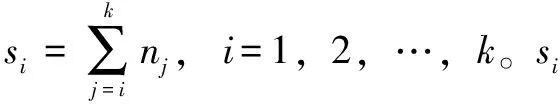
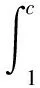
2.3 加权最小二乘法的参数估计

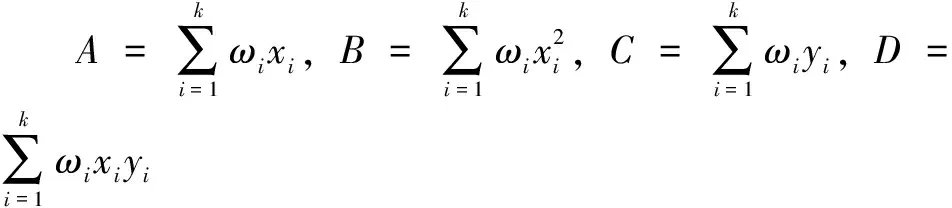
3 仿真算例分析




4 结论
