超高压高低温条件下节流阀Y形圈的影响因素分析
2024-03-13冯春宇钱齐徐明军杨忠武谢齐
冯春宇,钱齐,徐明军,杨忠武,谢齐
(1.西南石油大学机电工程学院,四川成都 610599;2.塔里木油田分公司克拉采油气管理区, 新疆库尔勒 841000;3.中电锦江信息产业有限公司,四川成都 610051)
Y形密封圈由于其优异的密封性能在天然气采集设备上被广泛使用。地底天然气开采出来之后压力高达120 MPa,此时需要节流阀进行降压节流,因此节流阀密封使用的Y形密封圈要求能在高低温、高压环境下稳定工作[1-2]。TOK等[3]研究表明,当Y形密封圈唇形密封偏心率增大,且唇厚值增大时,摩擦力矩也随之增大。崔凯波等[4]利用ABAQUS软件对Y形环橡胶密封在可变液压作用下的Mises应力、密封环变形和接触压力等性能进行仿真分析,对研究和掌握Y形密封圈的寿命规律具有一定参考价值。DONG等[5]的研究表明,封隔器橡胶的密封性能和强度特性受温度的影响很大,且Yeoh模型是更适合描述封隔器管高温材料的本构模型。SANG等[6]的研究表明,密封件的中间接触区存在着最大接触应力,随着外界压力的增加,最大接触应力和接触宽度有明显的增加。
但是目前国内外针对井场复杂工况下密封件的研究与分析较少。本文作者对PTFE及其改性材料Y形密封圈在高压、高低温工况下的性能进行了有限元分析;在ISIGHT中选用最优拉丁超立方试验对密封圈的唇前角、唇后角、宽度、基体高度、唇尖高度5个参数进行试验设计,拟合了尺寸与目标函数的二次响应曲面,选择多岛遗传算法,对Y形密封圈5个参数进行优化;最后将加工的试件进行PR2实验,验证了理论分析结果。
1 节流阀结构及密封材料
1.1 节流阀结构
天然气设备中的节流阀结构如图 1所示。文中研究的Y形圈密封是静密封,主要安装在底座和阀体之间,防止井口高压天然气不经过节流直接从底座与阀体之间的间隙流入节流阀出口,保护下游管线。Y形密封圈的温度工况选择-46~180 ℃,压力级别按照140 MPa(20 000 psi)设计。
1.2 密封材料
聚四氟乙烯(PTFE)是一种高分子工程塑料,化学稳定性高,使用温度范围宽,摩擦因数低,且具有优异的耐老化和耐辐射性能、极好的热稳定性[7]。但PTFE也存在强度不够,膨胀系数过大,再加工困难等问题。因此采用高温强度好、具有较高的断裂韧性、抗疲劳性能和抗蠕变性能的碳纤维[8],以及导热性好、模量高、拉伸强度和冲击强度高、断裂伸长率低、热稳定性好、价格低廉的玻璃纤维[9],对其进行了改性。
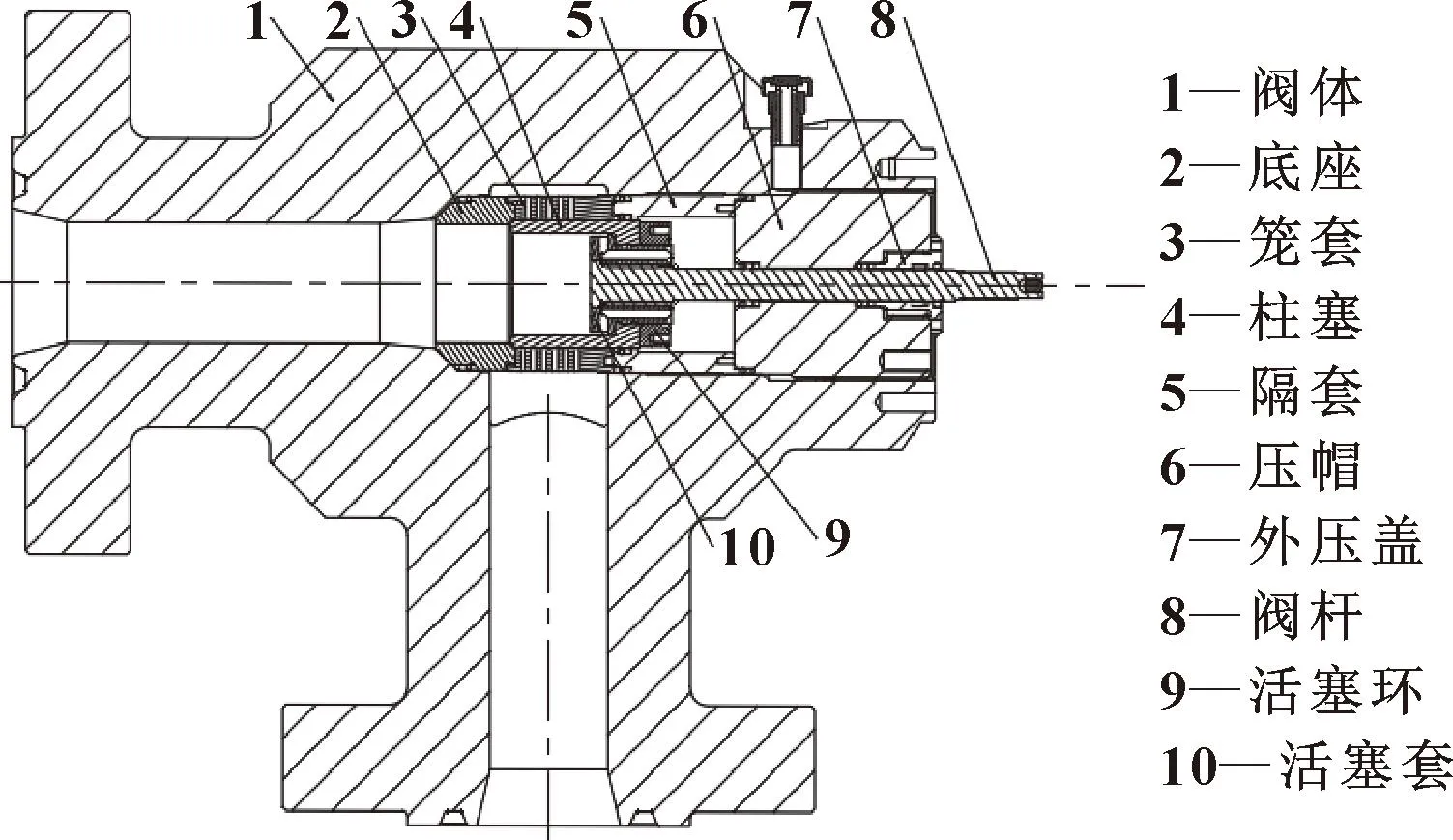
图1 节流阀内部结构Fig.1 Throttle valve internal structure
文中选择PTFE+5%碳纤维(5C-PTFE)、PTFE+5%碳纤维+5%玻璃纤维(5C5G-PTFE)、PTFE+10%碳纤维(10C-PTFE)、PTFE+10%碳纤维+10%玻璃纤维(10C10G-PTFE)4种改性材料开展研究。
2 Y形密封圈数值仿真
2.1 Neo-Hooke本构模型
由单轴拉伸试验得到不同温度下4种材料的应力应变数据,代入有限元软件的Evaluate模块对4种材料进行评估[10]。选取Neo-Hooke模型作为PTFE及其改性材料在不同温度下的本构模型。Neo-Hooke模型是Yeoh模型的一个简化的减缩多项式超弹性模型[11],该模型应变能表示为
W=C10(I1-3)
(1)
式中:C10为Yeoh模型系数;I1为第一应变张量不变量。
Neo-Hooke模型在小应变和中等应变情况下具有良好的稳定性,并且可用来预测其他变形方式下的曲线[12]。表1给出了3种温度下由ABAQUS计算出的材料参数。
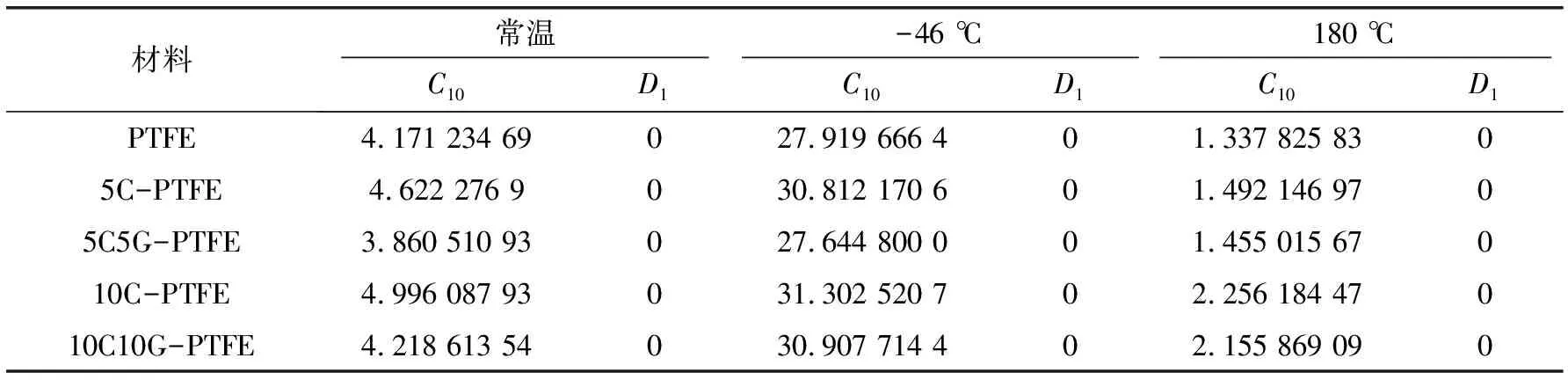
表1 各材料Neo-Hooke模型参数单位:MPa
2.2 Y形密封圈静态性能模拟分析
底座处密封有限元模型如图2所示。
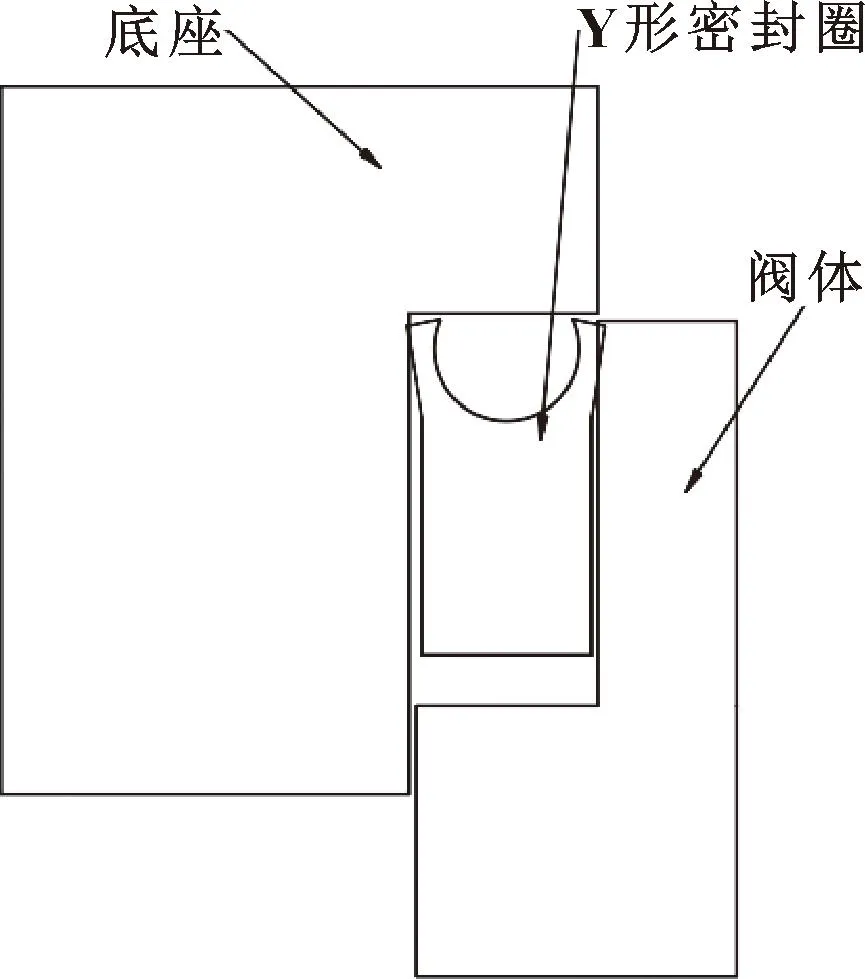
图2 底座处密封有限元模型Fig.2 Finite element model of the seal at the base
对建立的有限元模型作如下假设:
(1)将密封结构看作理想的完全轴对称模型;
(2)不考虑密封材料蠕变的影响,不考虑密封圈内弹簧的影响[13]。
Y形密封圈的静态性能模拟步骤为:
(1)模拟Y形密封圈装配过程,对底座进行全约束,给阀体一定的轴向位移;
(2)模拟加压过程,在密封唇口部位施加目标压力140 MPa,施加压力时选择平滑分析步施加压力。
图3(a)所示是Y形密封圈加压示意图。弹簧蓄能密封圈的有效密封部位是Y形圈的唇口,所以文中着重讨论过盈量、唇前角、唇后角的影响[14]。
Y形密封圈的网格单元类型为CAX4RH,如图3(b)所示,即单元属性是四结点双线性轴对称四边形单元、杂交、常压力、减缩积分及沙漏控制。

图3 弹簧蓄能密封加压示意(a)和Y形密封网格划分(b)Fig.3 Schematic of spring energized seal pressurization(a) and grid of Y-shaped seal(b)
2.3 Y形密封圈性能评价指标
Y形密封圈在密封沟槽的间隙会产生剪切应力,当剪切应力过大时会造成Y形密封圈的剪切破坏,引起密封失效。von Mises应力是基于剪切应变能的一种等效应力[15],可以作为评价Y形密封的抗破坏性能指标。当密封面接触压力大于其工作介质压力时,密封圈实现密封,即Y形密封圈起密封作用的条件是其最大接触压力值必须大于流体压力值。文中按图 4所示的内唇路径提取内唇边接触应力值。故Y形密封圈应同时满足von Mises应力和内唇边最大接触应力约束条件。
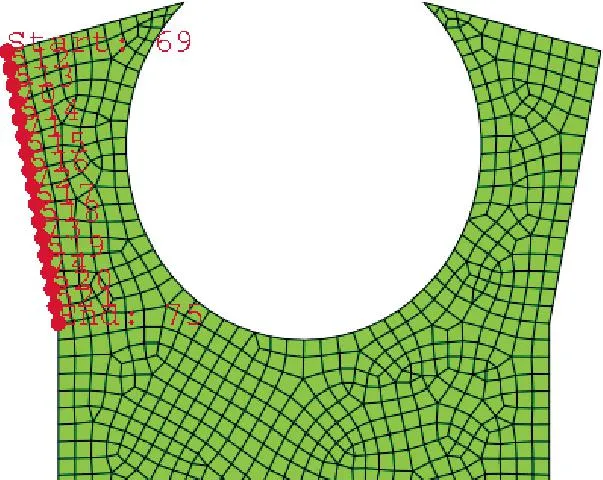
图4 内唇取值路径Fig.4 The value path of inner lip
2.4 过盈量对密封性能的影响
为了获得初始密封效果,在设计Y形密封圈时,内外唇都会设计有一定的过盈量。密封圈进入密封沟槽后,内外唇口与沟槽边相挤压,产生一定的预紧力,达到密封的效果,Y形密封圈的唇口过盈量δ如图 5所示。过盈量δ过小,密封唇口与接触面预紧力小,无法满足高压密封;δ值过大,会导致密封面之间摩擦增大,缩减使用寿命。为保证该密封件的密封性能和使用寿命要求,文中分别选取过盈量δ为0.10、0.15、0.20、0.25 mm进行有限元分析。

图5 唇口结构参数Fig.5 Lip structure parameters
图6示出了不同唇口过盈量下Y形密封圈的von Mises应力分布。可知,同一温度相同材料的最小von Mises应力随δ的增大而减小,表明采用较大过盈量有利于降低von Mises应力;同一过盈量相同温度下,von Mises应力值随碳纤维的含量增加而增加,即PTFE、5C-PTFE及10C-PTFE材料的von Mises应力依次增加,在添加与碳纤维相同比例的玻璃纤维后,最大Mises应力值有所下降。
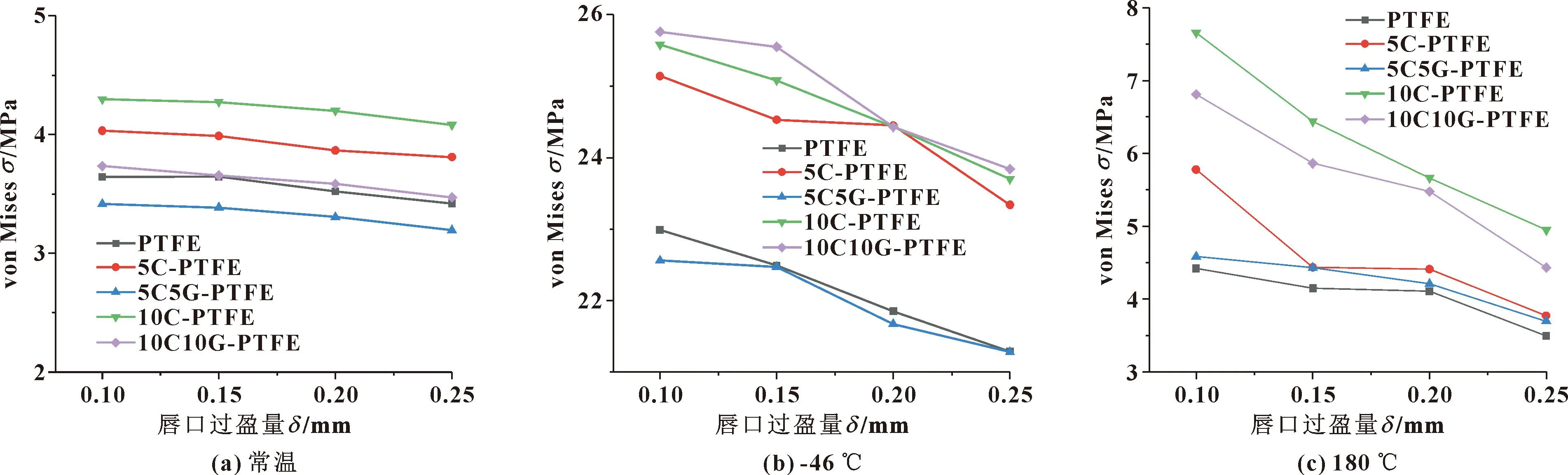
图6 不同唇口过盈量下Y形密封圈的von Mises应力Fig.6 Von Mises stress of Y-rings at different lip interference:(a)normal temperature;(b)-46 ℃;(c)180 ℃
图 7示出了不同唇口过盈量下Y形密封圈内唇最大接触应力分布。可知,内唇最大接触应力随过盈量的增加而增大,这是因为唇口过盈量越大,唇口产生的过盈力越大,在相同压力下产生的接触应力就越大。工作介质压力为140 MPa,因此当过盈量δ为0.20、0.25 mm时,能同时满足3种温度下的密封材料是5C-PTFE、10C-PTFE。
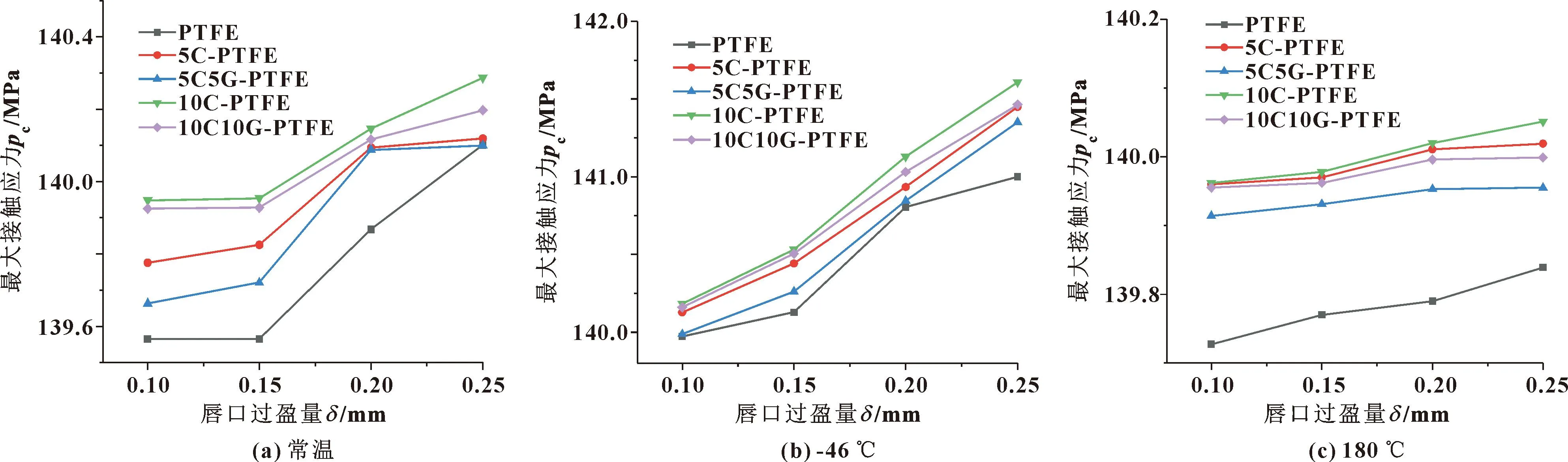
图7 不同唇口过盈量下Y形密封圈的内唇最大接触应力Fig.7 Maximum contact stress of the inner lip of Y-rings at different lip interference:(a)normal temperature;(b)-46 ℃;(c)180 ℃
在满足密封要求的前提下,各材料密封件在受140 MPa压力后,密封件的最大Mises应力均比相应材料的拉断应力小,满足强度要求。因唇口过盈量δ值过大时密封圈安装不易,在受压时唇口不易撑开;另外,初始过盈量过大将导致密封唇口与活动接触面间的摩擦力增大,唇口部位易磨损,导致密封圈使用寿命缩短,故在选择唇口过盈量时优先选择δ=0.20 mm。
2.5 唇前角对密封性能的影响
Y形密封圈油侧角b又称唇前角,是密封圈和天然气相连通的部分与轴之间的夹角;空气侧角a又称唇后角,是密封圈和空气侧相连通的部分与轴之间的夹角,如图 5所示。
在保证过盈量δ=0.20 mm和唇后角不变的前提下,选取不同唇前角进行数值分析。其中唇前角取b=71°~79°,增量取2°。
图8和图9分别示出了不同唇前角下Y形密封圈的von Mises应力和内唇最大接触应力。可见,PTFE及其改性材料密封件von Mises应力和内唇最大接触应力均随唇前角b的增大先增大后减小。当b=75°时,内唇最大接触应力最大,此时能同时满足抗破坏性能要求和密封性能要求的密封材料是10C-PTFE。

图8 不同唇前角下Y形密封圈的von Mises应力Fig.8 Von Mises stress of Y-rings under different lip angles:(a)normal temperature;(b)-46 ℃;(c)180 ℃

图9 不同唇前角下Y形密封圈的内唇最大接触应力Fig.9 Maximum contact stress of the inner lip of Y-rings with different lip angles:(a)normal temperature;(b)-46 ℃;(c)180 ℃
2.6 唇后角对密封性能的影响
当δ=0.20 mm和唇前角b=75°时,选取不同唇后角进行数值分析。其中唇后角取a=8°~16°,增量取2°。
图10和图11分别示出了不同唇后角下Y形密封圈的von Mises应力和内唇最大接触应力。可知,各材料最大Mises应力随密封件唇后角a增加呈现先增大后减小的趋势,内唇的最大接触应力均随唇后角的增大而增大,当a=14°和a=16°时,除PTFE外其余改性材料密封件均能够在3种温度下同时满足抗破坏性能要求和密封性能要求。

图10 不同唇后角下Y形密封圈的von Mises应力Fig.10 Von Mises stress of Y-rings under different lip back angles:(a)normal temperature;(b)-46 ℃;(c)180 ℃
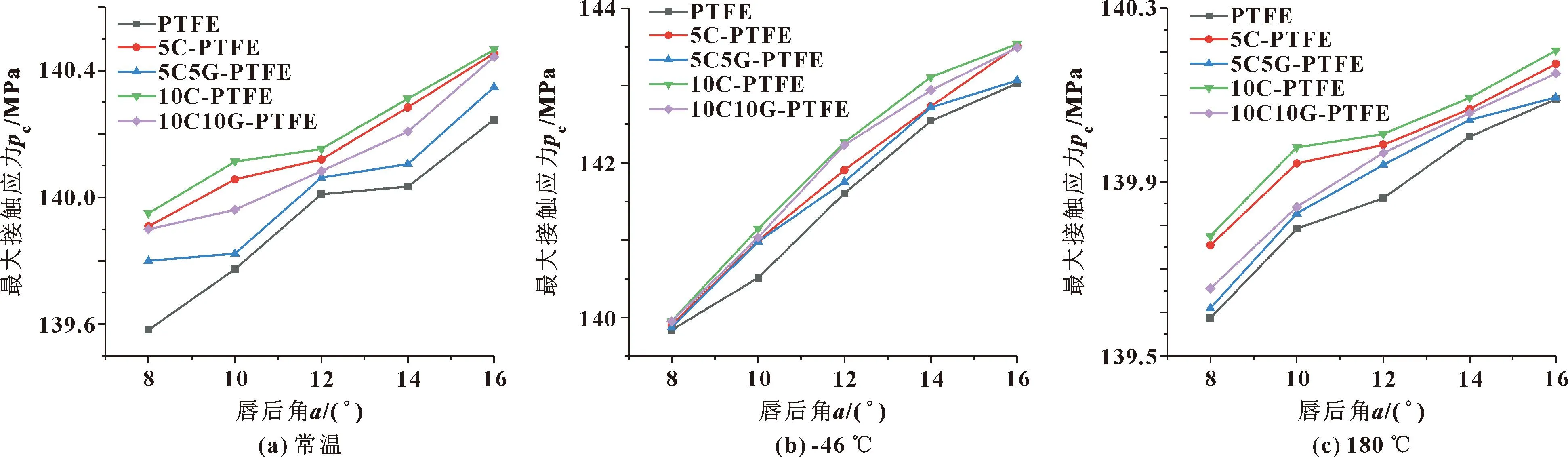
图11 不同唇后角下Y形密封圈的内唇最大接触应力Fig.11 Maximum contact stress of the inner lip of Y-rings at different lip back angles:(a)normal temperature;(b)-46 ℃;(c)180 ℃
3 Y形密封圈灵敏度分析及尺寸优化
3.1 Y形密封圈性能优化建模
图12所示是Y形密封圈参数化建模过程中的参数化模型,优化设计首先需要确定Y形密封的设计参数。
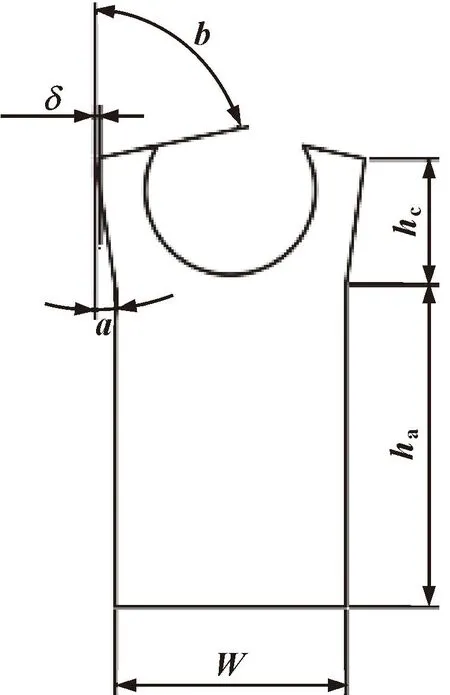
图12 Y形圈参数化模型Fig.12 Parametric model of Y-ring
根据Y形密封结构参数对密封性能影响的分析,确定Y形密封主唇部分的相关几何尺寸是设计变量。根据尽量增大主唇口的接触压力、尽量保证唇形密封圈结构强度的原则下,选取唇前角b,唇后角a,宽度w以及基体高度ha和唇尖高度hc5个参数作为设计变量。因此,用于Y形密封圈的数学优化模型表述如下。
(1)优化设计参数:
表2给出了5个参数的取值。将Y形密封圈的结构变量尺寸用向量表示为
X=[a,b,w,ha,hc]T
(2)
(2)约束条件
Y形密封圈最大von Mises应力是25.82 MPa,内唇接触区接触应力均要大于140 MPa,因此约束条件需要满足式(3)。
(3)
式中:σmax为最大von Mises应力;pc为内唇的最大接触应力。
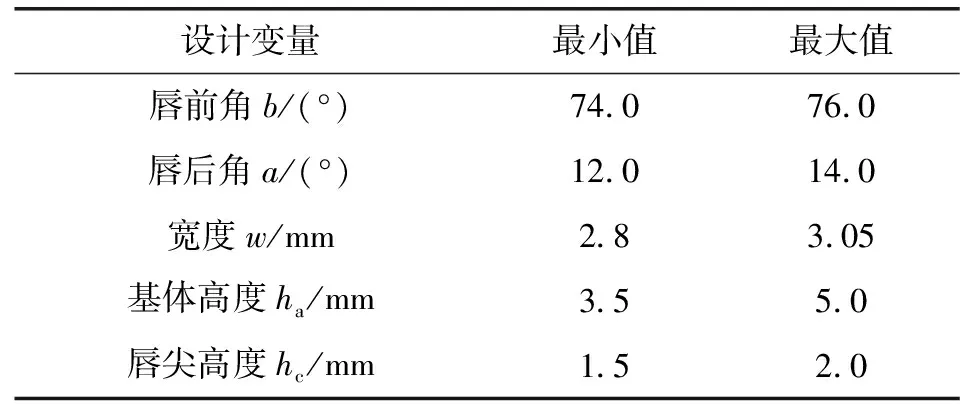
表2 Y形密封圈设计变量参数
(3)优化目标函数
在约束条件下,Y形密封圈的结构尺寸,达到Y形密封圈密封140 MPa(20 000 psi)的设计要求,得到优化结果。因此,Y形密封圈的优化目标函数为
(4)

3.2 密封圈灵敏度分析
通过灵敏度分析,首先确定对密封结构影响较大的几何参数,然后对尺寸进行优化,从而进一步提高结果质量。分析灵敏度r的定义如下:
(5)

将1 500个试验样本进行计算可以得到不同设计变量对密封性能指标参数的影响程度。计算结果中,有977组样本不能完成Y形密封圈的建模,523组样本能够完成整个流程的计算。
图13示出了Y形密封圈最大von Mises应力主效应。可见,Y形密封圈的宽度对静密封时的最大von Mises应力影响最大,宽度由低水平到高水平过程中最大Mises应力呈现下降的趋势;其余4个设计变量由低水平到高水平过程中最大Mises应力值变化幅度不大,对最大Mises应力影响较小。
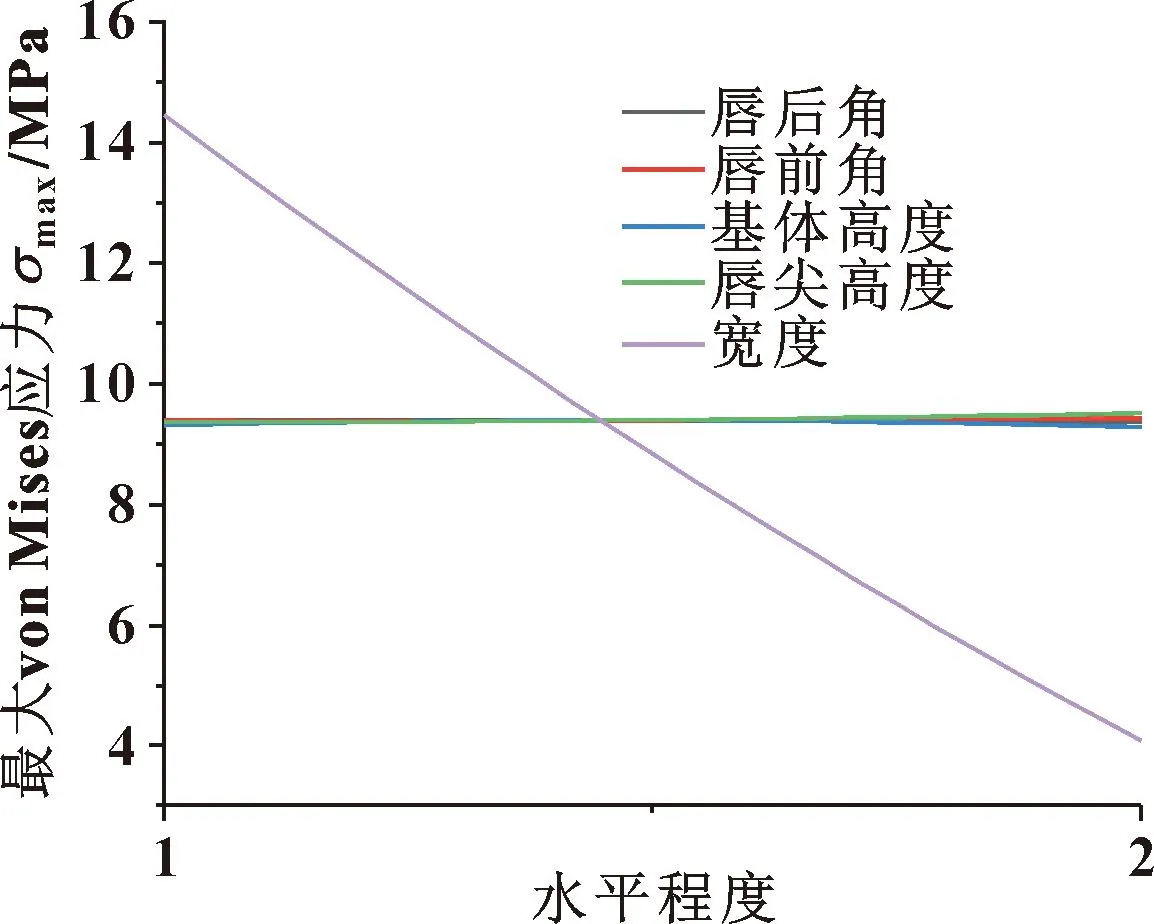
图13 Y形密封圈最大von Mises应力主效应(1代表 低水平,2代表高水平)Fig.13 Maximum von Mises stress main effect of Y-rings (1 for low level,2 for high level)
图14示出了阀杆静止时Y形密封圈内唇边最大接触应力主效应。可见,Y形密封圈的宽度对静密封内唇边最大接触应力影响最大,宽度由低水平到高水平过程中内唇边最大接触应力呈现增加的趋势;唇后角由低水平到高水平过程中内唇边最大接触应力呈现线性增加的趋势;基体高度由低水平到高水平过程中内唇边最大接触应力呈现减小的趋势;唇前角和唇尖高度由低水平到高水平过程中内唇边最大接触应力呈现先增大后减小的趋势,但变化不大。
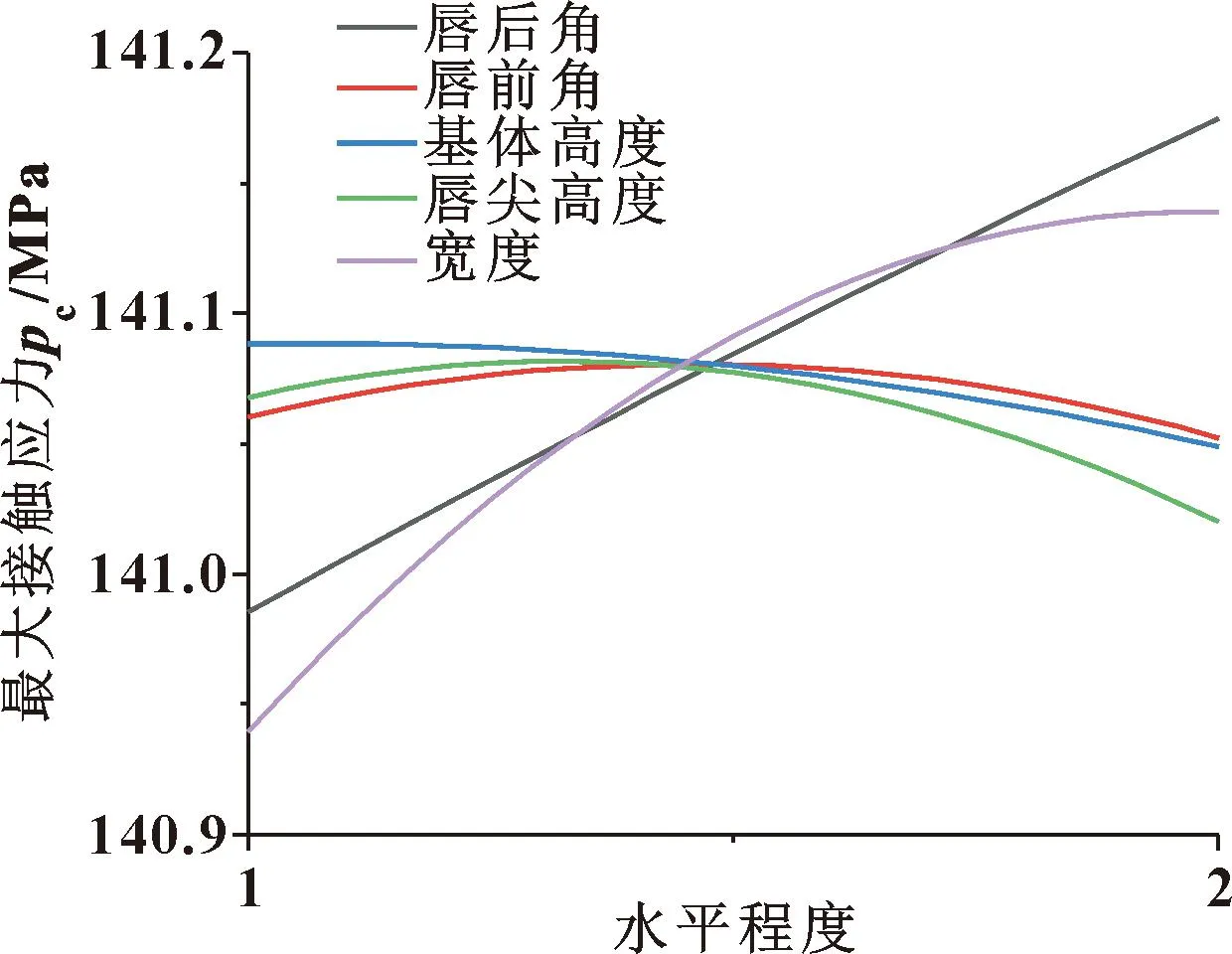
图14 阀杆静止时Y形密封圈内唇边最大接触应力主效应Fig.14 Main effect of the maximum contact stress on the inner lip of the Y-ring when the stem is stationary
图15示出了密封圈最大von Mises应力灵敏度,蓝色代表灵敏度为正,表示目标函数值随优化尺寸增大而增大;红色灵敏度为负,表示目标函数值随优化尺寸增大而减小。可知,各优化尺寸对于静密封时最大Mises应力的影响顺序为:w>hc>a>b>ha。
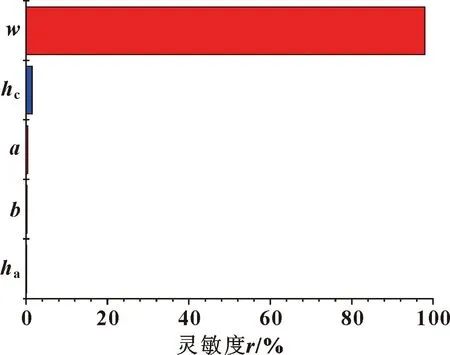
图15 密封圈最大von Mises应力灵敏度(蓝色表示 正效应,红色表示负效应)
图16示出了密封圈内唇边最大接触应力灵敏度。可看出,各优化尺寸对于静密封时最大接触应力的影响顺序为:w>a>ha>hc>b。
综上,在设计Y形密封圈时应该重点考虑密封圈基体宽度w、基体高度ha和唇尖高度hc的尺寸对密封圈性能的影响。
基于实验数据,利用响应面模型函数可以分析建立这些变量之间的经验关系,从而进一步预测性能。文中选取二阶响应面模型来拟合Y形密封圈的近似模型,如式(6)所示。二阶响应面模型需要[(N+1)(N+2)]/2次精确分析,根据输入样本点去拟合a0、bi、cij、di。
(6)
结合图15和图16的结论可以得到,对Y形密封圈最大Mises应力及内唇接触应力贡献度最大的是宽度w及基体高度ha的尺寸。图 17、图 18所示是这2个设计变量对目标函数的响应面。
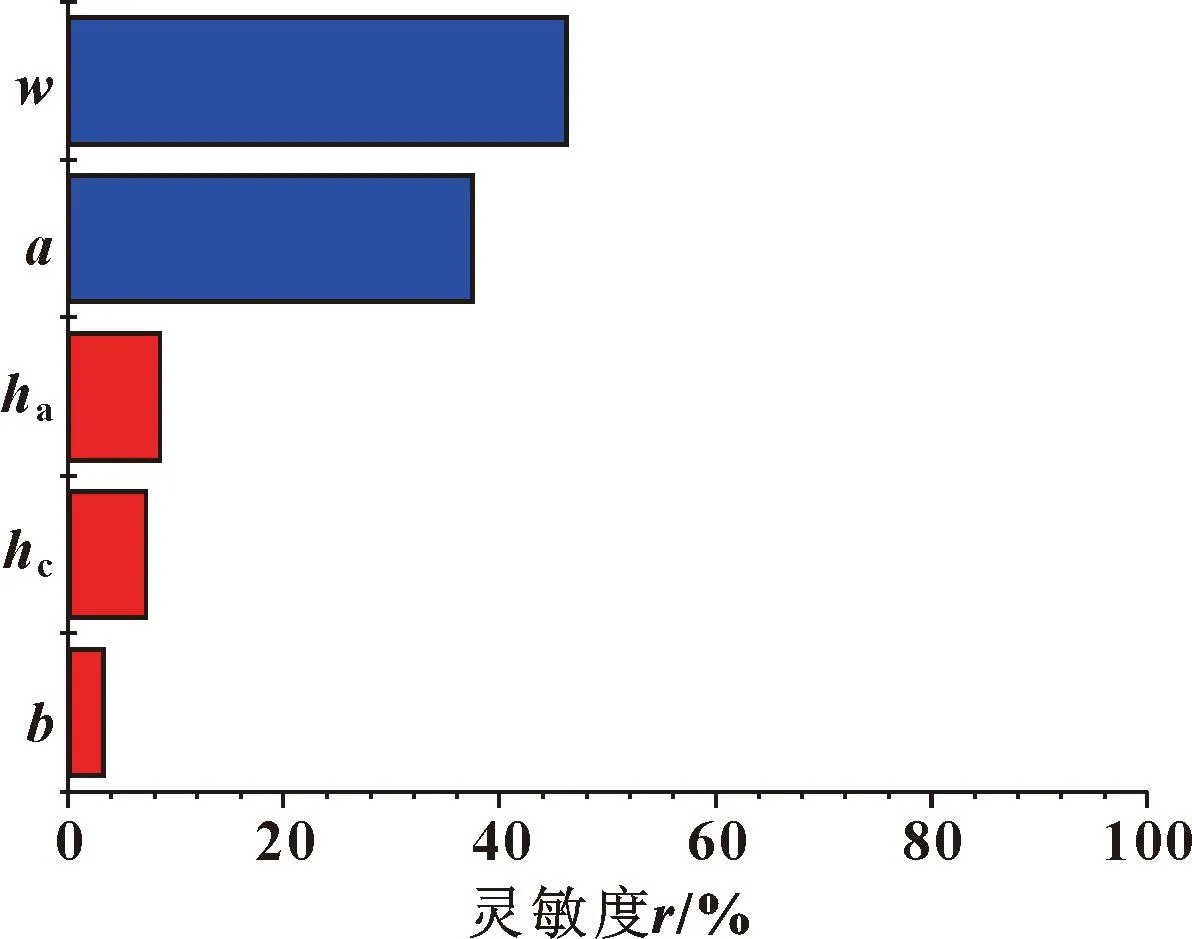
图16 密封圈内唇边最大接触应力灵敏度(蓝色 表示正效应,红色表示负效应)Fig.16 Maximum contact stress sensitivity of the maximum contact stress of the inner lip of sealing ring(blue represents positive effects,red represents negative effects)

图17 密封圈宽度及基体高度对von Mises应力响应面Fig.17 Response surface of sealing ring width and substrate height to the maximum von Mises stress
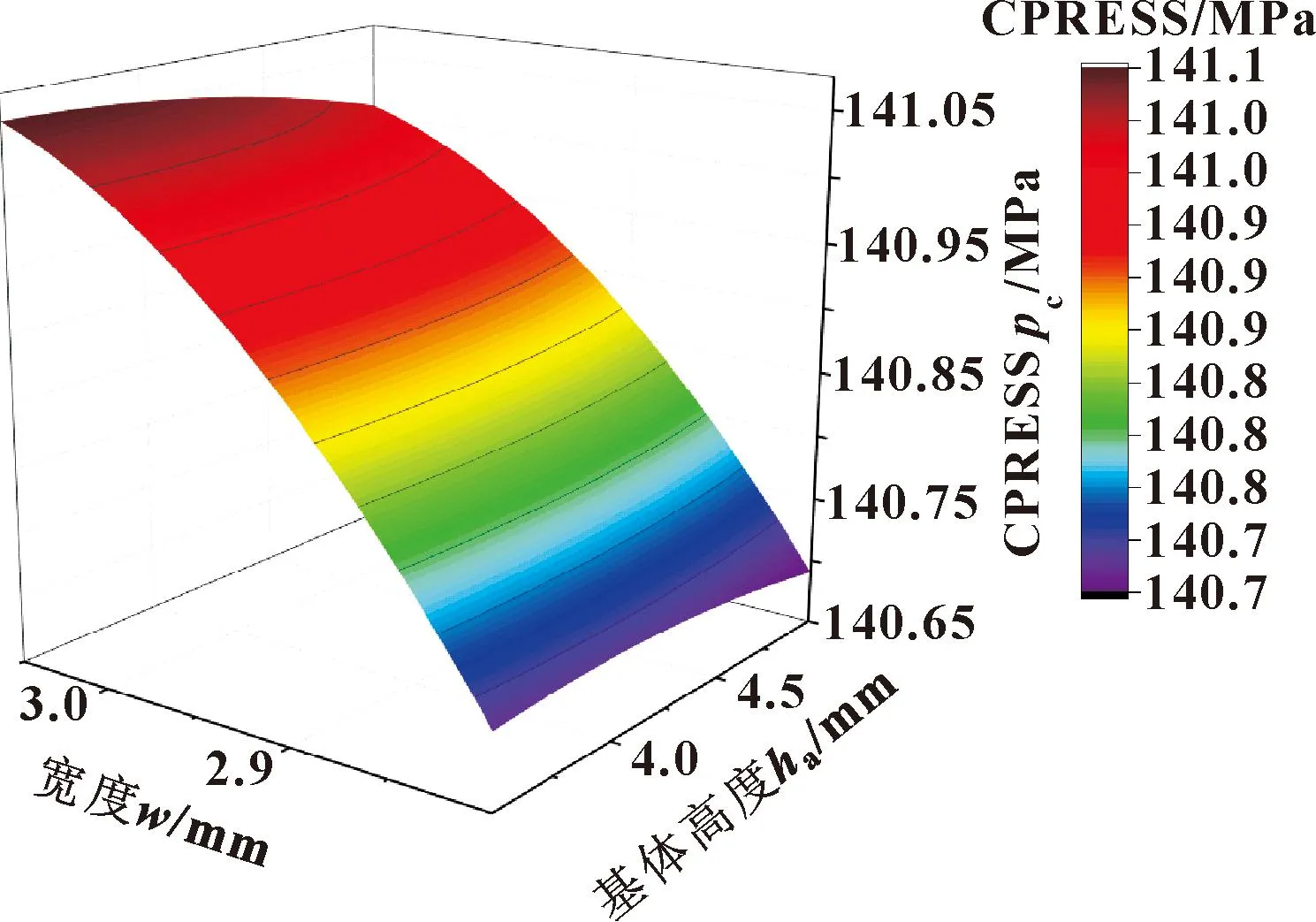
图18 密封圈宽度及基体高度对内唇边最大接触应力响应面Fig.18 Response surface of sealing ring width and substrate height to the maximum contact stress on the inner lip
3.3 基于多岛遗传算法的尺寸优化
遗传算法是一种参考自然界的遗传机制和自然选择特点而构造出的随机化搜索方法[17]。遗传算法寻找最优解时,优化问题的解被称之为“个体”,一定数目的“个体”可以组成一个“种群”。在进行优化解算时,种群里的每一个个体都会被系统评价,并通过计算适应度函数得到一定的适应度值,种群中的个体按照适应度值排序,适应度值高的排在前面。
文中多岛遗传算法参数设置如下:种群规模设定为100,岛数设定为10,进化代数设定为20,多岛遗传的运算总次数为三者乘积,一共为20 000次,岛与岛之间的交叉概率Pc=0.8,变异概率为Pm=0.01,迁徙概率设为0.01,岛与岛之间的迁徙间隔代数设定为5。经过19 971次迭代计算后收敛,可以得到图19和图20所示目标函数的历史寻优过程。历史进化过程图中,黑色点代表Y形密封圈优化搜索求解过程中的交叉解,蓝色的点代表非劣质解,红色点代表劣质解,绿色的点代表Y形密封圈优化问题的最优解。
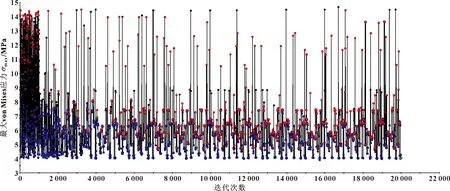
图19 密封圈最大von Mises应力寻优历程(黑色点代表交叉解,蓝色点代表非劣质解,红色点代表劣质解,绿色点代表最优解)Fig.19 Optimization process of maximum von Mises stress of the sealing ring (Black dots represent cross solutions,blue dots represent non inferior solutions,red dots represent inferior solutions,and green dots represent optimal solutions)

图20 密封圈内唇边最大接触应力寻优历程(黑色点代表交叉解,蓝色点代表非劣质解,红色点代表劣质解,绿色点最优解)Fig.20 Optimization process of maximum contact stress in the inner lip of the sealing ring (Black dots represent cross solutions,blue dots represent non inferior solutions,red dots represent inferior solutions,and green dots represent optimal solutions)
经过优化设计后得到的设计变量最优值如表 3所示。优化后的Y形密封圈最大von Mises应力值在3种温度下均小于10C-PTFE材料的拉伸强度,静密封时von Mises应力优化后下降了4.575 MPa;静密封时内唇边最大接触应力值增加了0.945 MPa。优化后密封圈的von Mises应力值有所下降,可以一定程度上提高使用寿命,同时内唇接触应力值有所提高,提高了密封能力。
4 Y形密封圈密封性能试验
根据前文分析的结果,采用10C-PTFE材料,按表3所示尺寸参数制备了Y形密封圈,并进行了密封试验。设计的工装如图 21所示,进行PR2测试的试压工作。Y形密封圈安装在图 21中的位置1、2、3处。

表3 设计变量最优值Tab.3 Optimal value of design variables
PR2性能测试除了静压力测试、压力循环测试、温度循环测试,还包括承载载荷循环测试、操作力循环测试、操作力矩循环测试等。
节流阀先按照API6A规定进行压力测试:
(1)首先将压力从0升压至试验压力207.0 MPa保压3 min,再将阀门完全开启使压力降至0,升压至试验压力207.0 MP保压3 min,在保压期间观测到的压力变化应小于3.45 MPa,且在保压期间应无可见渗漏。
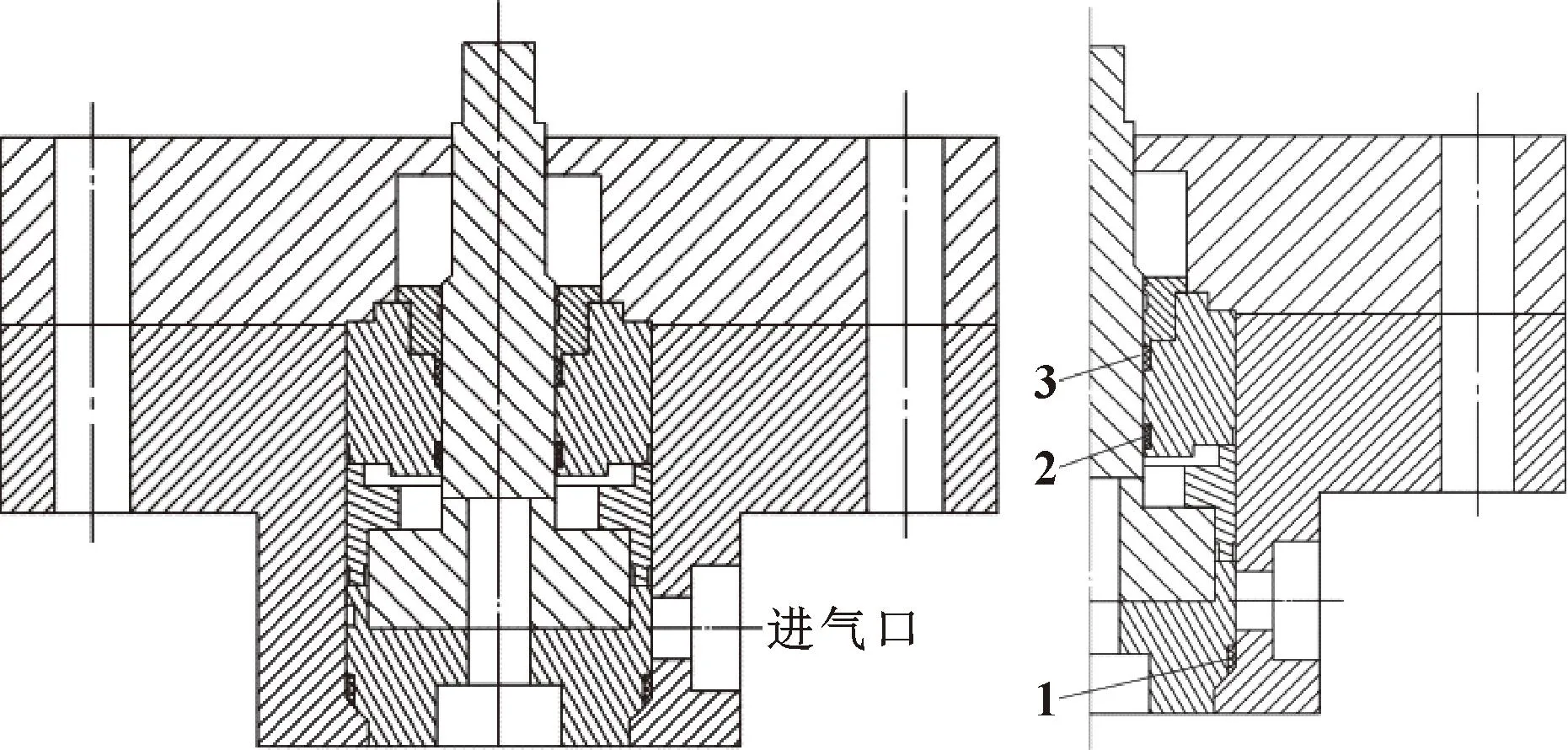
图21 气密封工装(Y形密封圈安装在1,2,3处)Fig.21 Airtight sealing tooling(Y-ring installed in 1,2,3)
(2)阀门部分开启,升压至额定工作压力138.0 MPa,保压3 min。在保压期间观测到的压力变化应小于3.45 MPa,且在保压期间应无可见渗漏。
节流阀压力测试合格后,按照API6A的试验方法,进行PR2试验,试验流程如下:
(1)室温下160次带压开、关循环试验:阀杆在额定工作压力138.0 MPa下至少进行160次开关循环,测量和记录在循环开始及结束时的开启扭矩和转动扭矩应小于等于200 N·m。
(2)最高温度和最低温度下的20次带压开、关循环试验:在180~191 ℃和-57~-46 ℃下,用气体作为试验介质,重复“室温下的开/关循环动态压力试验”的试验方法和要求,进行阀杆“开-关-开”循环20次动态循环试验。测量和记录在循环开始及结束时的开启扭矩和转动扭矩应小于等于350 N·m。
(3)进行气压试验,阀应为部分开启状态。先在额定工作压力138.0 MPa下保压960 s,再在5%~10%的额定工作压力2 MPa下保压960 s,试验后不释放压力,在保压期间应无可见连续气泡。若观测到渗漏,则在大气压下观测得到的渗漏量。在规定的保压期间阀杆密封渗漏量应小于60 mL/h,静密封渗漏量应小于(阀盖密封、端部连接)20 mL/h。
试验的节流阀Y形密封圈通过了PR2试验,实验过程中压力变化曲线如图22所示,并取得合格的检验报告。

图22 压力变化曲线Fig.22 Pressure change curves:(a)normal temperature; (b)-46 ℃;(c)180 ℃
5 结论
(1)由PTFE及其改性材料制备的Y形密封圈,在过盈量0.10~0.25 mm范围内,最大von Mises应力随唇口过盈量增加而减小;在唇前角71°~79°范围内,最大von Mises应力随唇前角的增大先增加后减小,在唇前角为75°时von Mises应力有最大值;在唇后角8°~16°范围内,最大von Mises随唇后角的增大呈现先增大后减小的趋势,在唇后角为14°时von Mises应力有最大值。
(2)Y形密封圈内唇最大接触应力随唇口过盈量的增加而增大,随唇前角的增加呈现先增大后减小的趋势,在唇前角为75°时内唇最大接触应力有最大值;内唇最大接触应力随唇后角的增加而增大。制备的10C-PTFE材料能够满足阀杆处静密封要求。
(3)密封圈基体宽度w、基体高度ha和唇尖高度hc的尺寸对密封圈性能的影响较大,最优尺寸为w=3.05 mm,ha=3.55 mm,hc=1.50 mm。
(4)按照优化参数设计制造了密封圈,并完成了节流阀的PR2试验。
