膨胀管实体膨胀锥受力分析与膨胀试验验证

2024-03-13郭慧娟王鑫赵运才

润滑与密封 2024年2期

郭慧娟，王鑫，赵运才

(1.中国石油集团工程技术研究院有限公司，北京 102200；2.江西理工大学机电工程学院，江西赣州 341000)

膨胀管(SET)技术通过膨胀管和膨胀锥组合，将膨胀管和锥体下到井内特殊地质层，以机械、液压或两者结合的方式驱动膨胀锥挤压膨胀管，使膨胀管内径扩大，实现有效封堵复杂地层、修复损坏套管及重复压裂等目的[1]。膨胀管的膨胀过程是从弹性状态到弹塑性状态最终达到完全塑性状态的过程，要求膨胀管具备较好的抗拉性、塑性、抗断裂性、延展性[2]。

膨胀锥作为膨胀管技术中的一个重要工具，在工作时受到极大的接触压力和摩擦力，因此要考虑膨胀锥的锥体结构、选材和润滑问题，要求其具有足够的强度、刚度、耐冲击性、耐磨损及耐腐蚀性等。目前改善膨胀锥耐磨性能的措施包括采用基材强化、优化膨胀锥结构、添加润滑脂、表面涂层、选用耐磨硬质材料，以实现最大程度减小锥体表面磨损，提高使用寿命，满足超长段膨胀要求。张仁勇等[3]选用模具钢Cr12MoV为基材，对其进行 1 020 ℃淬火+160 ℃低温回火处理，设计加工出小锥角(6°)的膨胀锥，采用自上而下的膨胀工艺对J55套管和316L不锈钢管进行径向膨胀试验。结果表明：经过回火处理后的 Cr12MoV膨胀锥满足工作要求，并顺利完成对J55套管和316L不锈钢管的径向膨胀。郭慧娟等[4]通过对不锈钢膨胀管进行不同锥角下的膨胀过程数值模拟，研究了锥角与膨胀压力、压力波动、膨胀后半径及轴向缩短量的关系。结果表明：随着锥角的增大，膨胀压力和启动压力都逐渐增大，轴向缩短量随着锥角的增大而减小，综合膨胀压力、膨胀后半径及压力波动，比较理想的膨胀锥锥角为15°～17°以及22°。任勇强等[5]采用等离子原位冶金技术，在膨胀锥用20CrMnTi低合金钢基体表面制备了Cr-Mn-Fe强化耐磨涂层，通过磨损试验机进行了磨损试验和硬度表征。结果表明，强化层的硬度高于20CrMnTi钢基体，强化层的相对耐磨性高出基材20CrMnTi钢10倍以上。魏松波等[6]采用超音速火焰喷涂技术在合金钢膨胀锥表面制备了碳化物硬质涂层，并进行摩擦磨损实验，结果表明，涂层使膨胀锥硬度提高了近60%，并显著降低了膨胀锥和膨胀管间的摩擦阻力，减轻了磨损，延长了膨胀锥的使用寿命。

目前，研究人员已广泛开展了基于弹塑性理论的膨胀力计算和利用有限元法的膨胀过程中膨胀力影响因素的研究。龚龙祥等[7]采用弹塑性理论，推导出膨胀管在弹性变形区和塑性变形区的周向应力和径向应力的数值计算模型，确定了膨胀管膨胀时在膨胀锥与膨胀管之间所需的最小接触载荷。张艳军和雷美荣[8-9]采用弹性理论分析的方法和主应力法对膨胀管进行力学分析，得到了膨胀管膨胀力理论计算模型。于洋等人[10]利用有限元数值模拟研究实体膨胀管的膨胀特性，探究了膨胀率、屈服强度、摩擦因数和膨胀锥锥角对膨胀力的影响规律。刘鹏等人[11]通过ANSYS软件对膨胀过程进行有限元分析，得到膨胀管的应力分布、膨胀力值、残余应力、轴向收缩量以及壁厚变化情况。然而，目前探究膨胀过程中膨胀锥体表面受力模型和应力分布的研究开展较少。因此，本文作者应用弹塑性理论推导了膨胀锥膨胀过程中的受力模型并采用ANSYS Workbench软件模拟了膨胀过程，研究膨胀锥表面应力、接触摩擦应力和膨胀推力变化情况，最后结合膨胀试验对有限元模拟结果进行了验证。研究结果可为膨胀锥设计、选材和膨胀管技术改进提供指导。

1 膨胀锥与膨胀管相互作用弹塑性力学行为理论分析

1.1 膨胀锥受力分析

膨胀锥分为定径膨胀锥和可变径膨胀锥，文中选择定径膨胀锥进行分析。膨胀锥在液压驱动下挤压膨胀管实现膨胀，膨胀锥受到液压推力、接触压力、滑动摩擦力[12-13]，图1所示为膨胀锥受力示意图。L1区域是导向区，用于引导膨胀锥前进和润滑液导出；L2是膨胀区，用于挤压膨胀管；L3是定径区，用于阻止膨胀管过大的回弹变形，保持最大膨胀半径。在膨胀过程中，由于速度较慢，且波动较小，近似为匀速直线运动受力平衡，因此在膨胀锥轴向方向上，由力的平衡关系可得：

图1 膨胀锥受力示意Fig.1 Schematic of force on expansion cone

dF=df·cosα+dNz

(1)

dNz=dN·sinα

(2)

由滑动摩擦力公式：

df=μ·dN

(3)

由式(1)、(2)、(3)可得：

(4)

df1=μ·dN1

(5)

式中：dF为该微单元受到的液压推力，N；dN为膨胀管反作用于微单元的接触压力，N；dN1为膨胀管反弹力，N；df为膨胀区微单元受到的滑动摩擦力，N；df1为定径区微单元受到的滑动摩擦力，N；α为膨胀锥锥角，(°)；μ为摩擦因数。

膨胀管对膨胀锥的反作用力主要是垂直于膨胀区表面的dN和垂直于定径区表面的dN1。dN沿r方向的分力dNr是膨胀管某个横截面达到塑性状态所需的最小力；dN沿z方向的分力dNz是膨胀管对膨胀锥的阻滞力。dN1为膨胀管介于不完全塑性变形向弹性变形转变的回弹压力。

1.2 膨胀管弹塑性力学分析

在膨胀过程中，随着膨胀锥通过，膨胀管先进入弹性形变，然后是弹塑性变形最后是塑性流动状态[14]。在该过程中涉及几何、材料和接触非线性[15]，因此膨胀锥受到膨胀管的反作用力是不连续变化量，难以用具体解析式表达。在膨胀管上取一厚度为dz的微单元进行弹塑性力学分析，微单元受力示意图如图2(a)所示。

由于膨胀锥的硬度远大于膨胀管，在分析过程中，假定膨胀锥的屈服强度远大于膨胀管的屈服强度，即膨胀锥的变形不予考虑，两者间的接触方式视为面-面接触。同时假定膨胀管：(1)材质具有各向同性，材料为理想弹塑性体；(2)是理想的同心圆管，壁厚均匀和横截面滚圆；(3)在每一个横截面周向方向内，应力分布均匀[16]。

由图2(a)可知，膨胀锥与膨胀管接触正压力为p，作用于膨胀管内壁。可将AB 边受压力p作用的四边形ABCD等效为AE边承受均布压力p作用的四边形AECF。

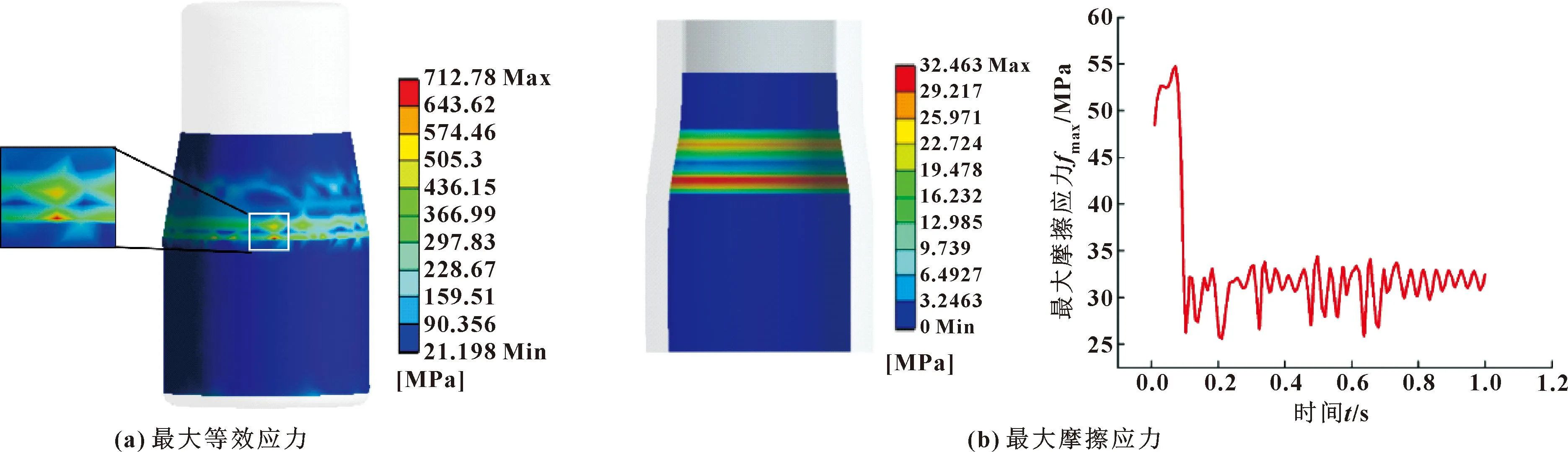
由于膨胀管满足理想同心圆管、壁厚均匀和横截面滚圆，且应力分布均匀，因此取高为dz的膨胀管段，在其任一横截面内，可视为轴对称平面应力问题。膨胀管横截面力学示意图如图2(b)所示，可知应力对称分布。在膨胀过程中，膨胀管单元体的位移、应力是径向坐标r与轴向坐标z的函数，与角坐标θ无关[17]，在膨胀锥的作用下，只产生沿半径r方向的膨胀。由于膨胀管是轴对称性弹塑性材料，在横截面上，设半径a处为弹塑性交界，可知a

在塑性区域内，各应力分量为

(6)

(7)

在弹性区内，由拉梅公式[19]，各应力分量为

(8)

(9)

由Mises屈服条件可得等效应力满足：

(10)

任取膨胀管一圆环面，设其半径为r(r1≤r≤r2)，对于平面轴对称问题，平衡方程为

(11)

由式(10)、(11)可得：

(12)

式中：σr为径向压应力；σθ为周向拉应力；σs为屈服极限。

边界条件满足：

σ(r=r1)=-p

(13)

σ(r=r2)=0

(14)

将边界条件式(13)代入式(12)，可得：

(15)

将式(15)代入式(12)可得：

(16)

将式(14)代入式(16)，可得：

(17)

在膨胀管周向上，要使某个膨胀管横截面全部进入塑性状态，即a=r2塑性区扩展到外壁，需在膨胀管内壁施加不小于p的压力，因此p是膨胀锥使膨胀管某个横截面全部达到塑性状态所要施加的最小压力，主要受材料屈服强度的影响。由牛顿第三定律可知，当膨胀管某个横截面刚达到塑性变形时，膨胀锥表面受到膨胀管的压力为-p。

对于膨胀锥，膨胀管反作用于膨胀锥表面的压力-p，其方向与dNr相同。由压力的计算公式可得：

dNr=pdS

(18)

(19)

由式(17)、(18)、(19)可得：

(20)

式中：R1为膨胀锥小径，mm；R2为膨胀锥大径，mm。

由三角函数定义：

(21)

(22)

由式(20)、(21)、(22)可得：

(23)

(24)

将式(24)代入式(3)，可得：

(25)

在定径区，假设膨胀锥受到膨胀管的反作用压力也是-p。同理可得：

dN1=p·dS1

(26)

S1=2πR2L3

(27)

由式(17)、(26)、(27)可得：

(28)

同理可得，滑动摩擦力f1为

(29)

因此影响膨胀锥接触压力和摩擦力的主要因素是膨胀管屈服强度和膨胀锥锥角。

2 膨胀锥受力有限元分析

在膨胀过程中，膨胀管与膨胀锥不断产生新的接触面，难以用解析法表达膨胀管变形时的每一个状态量，但基于非线性连续介质的有限元分析模拟方法，能为解决塑性大变形等非线性问题提供可视化解析，对膨胀管技术这类问题的模拟提供极大方便[20]。

2.1 模型建立

膨胀锥与膨胀管接触属于面-面接触大变形问题，在膨胀过程中存在摩擦和生热。文中利用ANSYS Workbench进行仿真模拟，选择静力分析解法求解膨胀锥表面应力分布情况，包括等效von Mises应力、摩擦应力和膨胀力。

膨胀锥选用冷作模具钢Cr12MoV，该材料具有较高的硬度和耐磨性，符合膨胀锥选材；膨胀管选用不锈钢，将其视为理想弹塑性模型，不考虑材料的强化性质，忽略屈服上极限影响[21]，即膨胀管在膨胀锥的挤压下，先进入线弹性阶段，然后是塑性流动状态。2种材料主要力学性能参数如表1所示。膨胀管双线性等向强化模型曲线如图3所示。

表1 材料性能参数

图3 双线性等向强化曲线Fig.3 Bilinear isotropic strengthening curve

采用三维建模软件SolidWorks对膨胀锥和膨胀管进行建模，对膨胀锥小径和大径处进行倒圆角处理，减小应力集中效应。文中对建模尺寸进行了等比例缩小，以有效减少网格单元，提高计算效率。建模参数如表2所示。

表2 建模尺寸参数

在接触设置时，因膨胀锥硬度远大于膨胀管，选定膨胀锥膨胀区和定径区外表面为目标面，膨胀管内壁为接触面，接触方式为面-面接触，目标面和接触面均为柔性体[22-23]，设为摩擦接触类型，摩擦因数为0.1，计算方程为纯罚函数。接触对选择如图4(a)、4(b)所示。

2.2 网格划分

在分析过程中，计算结果的精度和收敛性取决于建模的合理性和网格划分的质量。由于膨胀锥的整体尺寸相对于膨胀管来说较小，所以对膨胀锥网格进行细化，这样避免模型整体采用较小的网格尺寸导致划分的单元数过多从而使计算时间太长或者不收敛。文中利用ANSYS Workbench Mesh进行网格划分，其中，膨胀锥采用四面体单元，网格尺寸为2 mm，膨胀管采用自由划分，网格尺寸设为5 mm，网格物理选项设为非线性结构。划分网格后的膨胀锥有限元模型如图4(c)所示。

2.3 边界条件

在ANSYS Workbench中，载荷和约束是模型求解的边界条件。对膨胀管的下端圆环面设为Y方向无位移约束，上端自由。对膨胀锥底面设为Y正向移动120 mm，其他方向自由度为0。边界条件设置如图4(d)所示。

图4 模型前处理Fig.4 Model preprocessing：(a)target face；(b)contact face； (c)finite element mesh model；(d)boundary condition

2.4 有限元计算结果与分析

为便于计算，做如下简化假设：(1)膨胀锥的运动，属于缓慢匀速直线运动，即视为受力平衡；(2)摩擦因数恒定；(3)因膨胀速度缓慢忽略摩擦生热；(4)在计算过程中无润滑条件，视膨胀锥与膨胀管之间为干摩擦；(5)膨胀管材料沿各个方向力学性能相同；(6)膨胀管为理想弹塑性材料。

为了降低计算量，调整接触法向刚度因子为0.1，设置初始接触与渗透条件以及载荷子步选项控制，打开大变形，最后进行求解。

2.4.1 应力分析

以膨胀锥接触面为研究对象，得到最终载荷子步下的等效von Mises应力、摩擦应力结果，如图5所示。由图 5(a)可知，膨胀锥在膨胀过程中受到极大的界面应力，最大等效应力集中在大径处，原因是该区域受到接触力、摩擦力以及膨胀管弹性和挤压等多重作用，同时该区域是最大膨胀半径，对膨胀管挤压程度最强烈，最大等效应力712.78 MPa。

由图5(b)中的摩擦应力云图可知，膨胀锥与膨胀管接触面上最大摩擦应力集中在膨胀锥小径和大径处，最大摩擦应力达到32.463 MPa。原因是膨胀锥小径处最先与膨胀管接触，受到膨胀管弹性挤压导致该处的摩擦应力较大，而在大径处对膨胀管的挤压程度最强烈，且有接触应力集中，因此该处摩擦应力最大。由图5(b)中的最大摩擦应力随时间变化曲线可知，最大摩擦应力呈先增大再减小最后趋于相对稳定的变化趋势。在时间为0时最大摩擦应力为47 MPa，其原因归结于建模时设置了过盈，因此模拟开始时存在一定的摩擦应力；在0.1 s时最大摩擦应力达到峰值55 MPa，是由于膨胀管刚被膨胀时任何一段都处于弹性状态，且在0.1 s之前是静摩擦状态，因此该处是最大静摩擦力。当膨胀锥逐渐进入后，由于先被膨胀的膨胀管开始进入塑性变形状态，内径也开始变大，因此对膨胀锥作用力逐渐减弱；当膨胀锥完全进入膨胀管后，膨胀达到相对稳定状态，因此摩擦应力趋于相对平稳状态，但存在一定的波动，原因是在膨胀管膨胀方向上，膨胀管每一段依次进入弹塑性变形到塑性流动状态，由于经历的状态不同，因此摩擦应力出现波动。

图5 有限元计算结果Fig.5 Finite element calculation results：(a) maximum equivalent stress；(b) maximum friction stress

2.4.2 接触分析

有限元模拟结果与膨胀试验在不同时间段的接触状态如图6(a)所示[24]。可知，随着膨胀锥进入膨胀管，膨胀管端口呈现“喇叭状”，当膨胀管前端口通过膨胀锥大径后，两者之间并没完全接触，主要与膨胀区接触，其他区域存在较小的间隙。其主要原因是膨胀管弯曲强度较大，同时设置了膨胀管为理想弹塑性模型，因此被膨胀后的状态会一直保持。

图6(b)所示为最终载荷子步状态。可以得出，在膨胀过程中，膨胀锥膨胀区与膨胀管并没完全贴合，对于膨胀锥而言，小径处受拉应力，大径处受压应力，最大压应力为397.35 MPa，集中在大径上。

图6 膨胀管与膨胀锥接触状态Fig.6 Contact state between expansion tube and expansion cone：(a) state in different time periods；(b) state of final load sub-step

2.4.3 膨胀力分析

在膨胀管技术中，膨胀力是评价膨胀管技术的关键参数，其大小直接影响着膨胀成形和施工过程的难易程度，同时对膨胀锥的寿命、密封系统的完整性都有影响。由于膨胀力显著影响膨胀变形过程，因此在满足膨胀管塑性成形的前提下，较小的膨胀力不仅可以使膨胀过程顺利、减小施工难度，还可以保持膨胀管密封完整性，避免过大的膨胀推力导致管壁或密封环破裂失效甚至导致膨胀锥磨损过快。由于假定了膨胀过程属于缓慢匀速直线运动，轴向受力平衡，因此提取膨胀锥底部在轴向方向的推力即为膨胀力。图7所示为锥底推力随时间变化曲线。可知，在膨胀过程中，膨胀力先迅速增大，最大膨胀力为118 kN，之后在108～118 kN 之间出现小幅度波动。

图7 锥底推力随时间变化曲线Fig.7 Change curve of cone bottom thrust with time

3 试验验证

3.1 膨胀试验

选用20G材质的碳素结构钢膨胀管，尺寸为φ89 mm×7 mm，膨胀锥(锥角12°)选用Cr12MoV模具钢，最大直径为85 mm，如图8(a)所示。将发射腔、膨胀锥、膨胀管、连接杆、高压管线、压力表等连接，连接铝丝堵，完成膨胀系统组装[25-26]，如图8(b)所示。

图8 膨胀锥和膨胀系统组成Fig.8 Expansion cone(a) and expansion system composition(b)

膨胀试验得到的膨胀压力随时间变化曲线如图9所示。可知在打压膨胀过程中，膨胀压力先升高再相对稳定最后骤降为0。膨胀压力在33.6～43.2 MPa之间波动，最大膨胀压力为43.2 MPa。当膨胀锥脱离膨胀管后，膨胀压力迅速减小为0。

图9 试验得到的膨胀压力随时间变化曲线Fig.9 The change curve of expansion pressure with time obtained from the experiment

3.2 有限元模拟结果与试验对比

有限元计算与膨胀试验对比结果如表3所示。可知，有限元模拟结果值大于试验值，平均误差8%。其主要原因是有限元模拟中设置的膨胀管屈服强度为345 MPa，而试验采用是20G结构钢膨胀管，屈服强度只有230～250 MPa，因此会造成有限元模拟值大于试验值。同时在限元模拟中膨胀压力波动幅度较小，只有3.69 MPa，而试验得到的压力波动幅度达到9.6 MPa。主要原因为有限元模拟时膨胀管属于理想弹塑性材料，而试验中膨胀管要经历弹性形变到弹塑性状态和塑性流动状态，另外还受试验设备和方法的影响，因此试验值波动幅度更大。

有限元计算与膨胀试验结果的误差符合工程误差范围，证明了该有限元模拟的合理性。