七自由度机械臂逆运动学求解方法
2024-03-12段文杰张海博
曹 行, 何 俊*, 段文杰, 张海博
1. 上海交通大学 机械与动力工程学院, 上海 200240
2. 北京控制工程研究所, 北京 100094
0 引 言
为高效开发利用轨道资源和清理轨道碎片,美国提出MEV(mission extension vehicle)计划,德国提出DOES(deutsche orbitale service mission)计划[1-3]开展基于空间七自由度机械臂的在轨维修、拼接组装和燃料加注等问题的技术研究和探索[4-6].七自由度机械臂通常有两种结构:1)具有俯仰运动副的七自由度机械臂,由二自由度肩关节、三自由度肘关节和二自由度腕关节组成,其中第3、4和5关节互相平行; 2)SRS (spherical-roll-spherical-joint)结构的七自由度机械臂,具有3个相互垂直自由度的肩、腕关节和单自由度的肘关节[7].本文主要研究具有SRS结构机械臂的逆运动学求解问题.
空间机械臂控制的实时性要求高,逆运动学通常采用解析法[8].对于一个确定的末端位姿,SRS机械臂的关节空间内存在无数组解,因此需要设定冗余参数求出逆运动学解析解[9].时凯飞等[10]将七自由度机械臂的关节3固定为0°和180°,从而等效为六自由度机械臂求解出解析逆解.徐俊虎等[11]选取关节3作为冗余角,通过冗余差分角法确定冗余角并实现运动学的优化.HOLLERBACH[12]首次利用肩、肘和腕关节构成的平面和参考平面之间的夹角来描述机械臂构型,而参考平面表示SRS机械臂自运动的0°平面.SHIMIZU等[13]基于臂型角参数化的方法求出SRS机械臂的逆运动学解析解,此方法同样适用于关节极限位置.ZHOU等[14]对各关节角进行约束求出臂型角的变化范围,根据末端姿态确定最佳臂型角,最后求解出机械臂的逆运动性解析解.徐文福等[15]采用参数化臂型角的方法,将非偏置的SRS机械臂扩展到具有关节偏置结构的SRS机械臂,求解偏置七自由度机械臂逆运动学,但求解结果会存在误差.针对这一问题,MA等[16]结合关节角参数化的逆运动学求解方法,对基于臂型角参数化的偏置SRS机械臂的解析解进行修正,进而提高求解的精度.上述研究都为基于臂型角的SRS型机械臂的逆运动学求解奠定了理论基础.
本文以全物理仿真工况为背景,研究SRS机械臂处于吊丝卸载重力环境下水平方向的抓取运动.此背景下SRS机械臂末端通过奇异点,且要求在竖直方向运动较小,已有的臂型角定义方法难以适应此约束条件.本文根据目标位置设置臂型角,提出了一种基于臂型角规划的逆运动学求解方法,通过UG-Simulink联合仿真以及包含重力卸载装置的物理试验,验证了所提方法的有效性.
1 运动学建模
1.1 正运动学建模
SRS机械臂的DH (denavit-hartenberg)坐标系如图1所示,DH参数如表1所示. 本文采用S、E和W来表示SRS机械臂的肩关节、肘关节和腕关节中心,肘部偏置中心用E′表示. 图1中O为基坐标的原点,ai表示连杆长度,αi表示相邻2个关节轴线在连杆长度ai的法平面内投影角度,di表示相邻2个关节之间的公垂线度,θi表示关节转角.
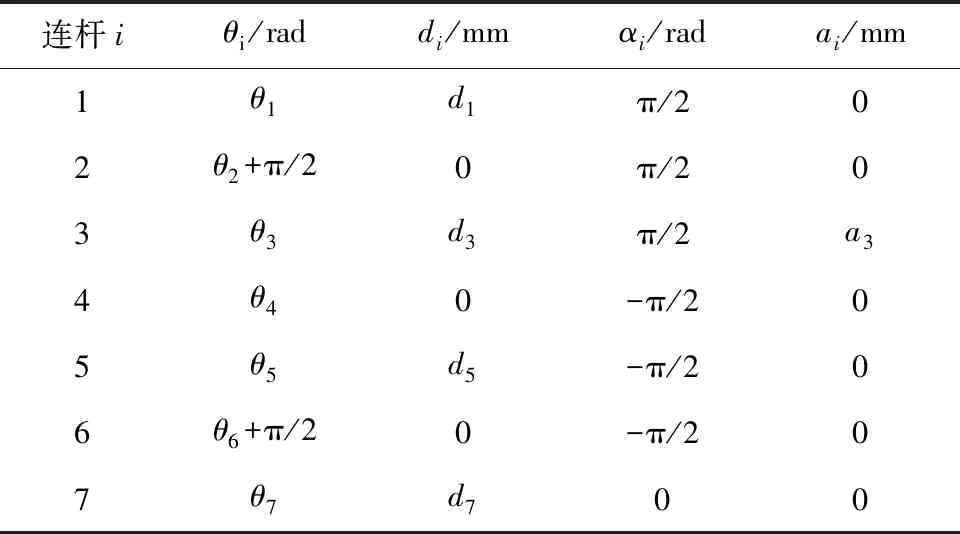
表1 SRS机械臂DH参数表Tab.1 The DH parameters of SRS manipulator
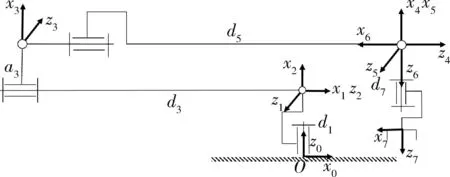
图1 SRS机械臂的DH坐标系Fig.1 The DH coordinate system of SRS manipulator
1.2 臂型角定义
如图2所示,O-xyz为机械臂的基坐标系,记向量OS=s,SW=w,SE=e.臂型角为参考平面和臂平面之间的夹角,其中参考平面是由w和任意单位向量v构成的平面,向量v根据目标位置进行设置.臂平面是由w、e构成的平面,即机械臂机体构成的平面.

图2 臂平面、参考平面和臂型角示意图Fig.2 The sketch map of arm plane, reference plane and arm-angle
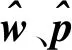

(1)
臂型角φ为
(2)
2 逆运动学求解
2.1 基于臂型角的逆运动学求解
当机械臂的末端位姿和臂型角φ已知,机械臂腕点W的位置OW=pw=[pwxpwypwz]T可以通过末端位姿和正运动学求出
(3)
(4)
假设ci=cosθi,si=sinθi,式(3)和(4)对应项相等可得
c1[s2(d3+d5c4)+c2s3(a3-d5s4)]+
s1s3(a3-d5s4)=pwx
(5)
s1[s2(d3+d5c4)+c2s3(a3-d5s4)]-
c1s3(a3-d5s4)=pwy
(6)
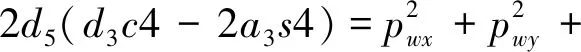
(7)
式(5)~(7)中各式平方相加化简得
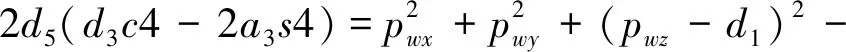
(8)
因此,θ4的大小为
(9)
根据罗德里格斯公式,空间向量k围绕单位向量p旋转α的旋转矩阵为
Rp,α=Ja+Jbcosα+Jcsinα
(10)
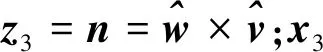
x3=Rn,π/2Rn,αw,y3=z3×x3
(11)
臂型角φ为0时肘关节的姿态矩阵
(12)
因此臂型角为φ的肘关节姿态矩阵为
(13)
肘关节姿态矩阵可以通过正运动学式求出
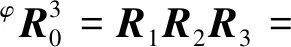
(14)
式(13)和(14)对应项相等,求出前3个关节的关节角

(15)
当求出前4个关节角度,通过姿态矩阵求出后3个关节角
(16)
(17)
式(16)和式(17)对应项相等求出θ5、θ6和θ7

(18)
对于给定的一组末端位姿和臂型角φ,可以通过式(9)、(15)和(18)求出各个关节的关节角.
当机械臂的位形使向量w和v共线时臂型角不存在,无法通过上述的计算过程进行逆运动学求解,此时可以根据肘部的空间位置约束进行逆运动学求解.
图2中,假设E在基坐标系下的坐标位置为[xEyEzE]T,根据SRS机械臂的几何结构特征有
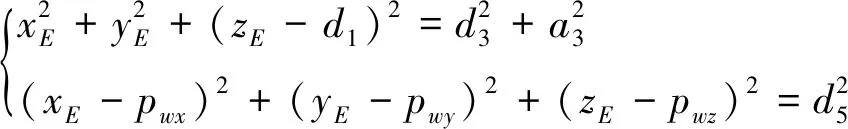
(19)
假设肘部在基坐标系的y轴存在位置约束,即yE为常数.由式(20)求出xE和zE
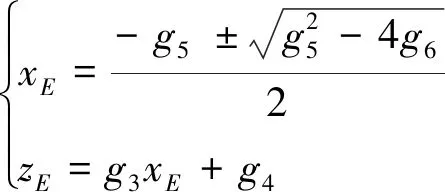
(20)
式(20)中
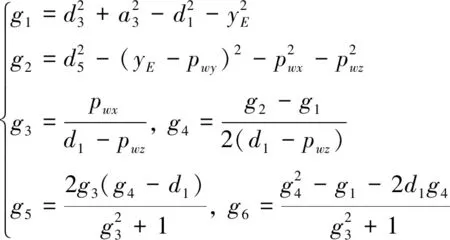
(21)
由此求出肘部E的坐标,这样可以计算肘部的姿态矩阵:z3轴垂直于臂平面,x3轴由向量e围绕z3轴逆时针旋转∠SEE′求得
(22)
求出肘关节的姿态矩阵后,各关节角度同样可以根据式(14)~(18)求解.
2.2 臂型角规划
通过式(2)计算出起始位置臂型角,根据任务要求设置目标位置臂型角的大小. 当在笛卡尔空间进行路径规划控制机械臂的运动时,采用直线插值方法规划从初值位置到目标位置的臂型角的变化. 当在关节空间进行路径规划时,臂型角的变化和关节的规划方式有关.
3 仿真与试验
3.1 UG-Simulink联合仿真
本文在UG-Simulink虚拟仿真环境中验证包含肩关节奇异点路径的逆运动解算过程.仿真中,机械臂末端初始位置和欧拉角设置为[-550 0 2 245]T、[90° 90° 0°]T,且末端姿态保持不变. 目标位置为[4 500 0 2 245]T.在笛卡尔空间中采用直线路径规划机械臂的运动轨迹,末端沿x轴匀速运动1 000 mm,时间为12 s. 机械臂位于初始位置时臂型角为0. 093 rad,设置目标位置的臂型角为0 rad,采用直线插值对臂型角进行规划.
图3为机械臂末端的位置变化曲线,在5.5 s时x=0,机械臂位于肩关节奇异位置.图4为机械臂关节角度变化曲线,曲线变化光滑连续,符合机械臂运动要求.图5为臂型角的变化曲线,曲线从初始0.093 rad线性减小至0 rad,曲线变化和规划一致.仿真结果表明本文提出的逆运动求解方法可以使机械臂平稳通过包含肩关节奇异点的路径.
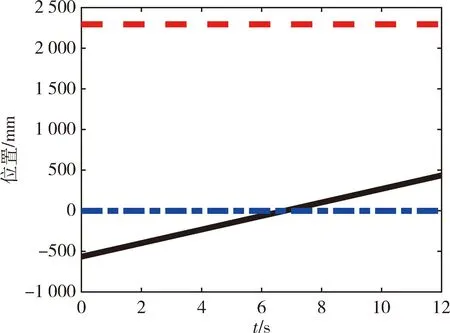
图3 仿真的末端位置变化Fig.3 Changes in the end position of simulation

图4 仿真的关节位置变化曲线Fig.4 Changes in the joint position of simulation
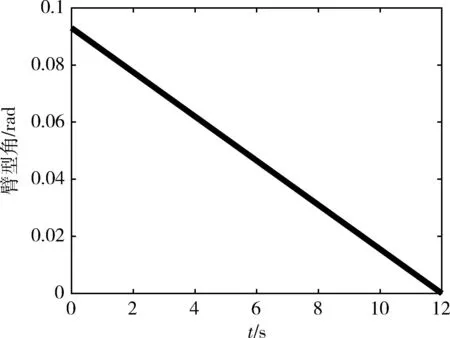
图5 仿真臂型角的变化Fig.5 Changes in the arm-angle of simulation
3.2 物理试验
图6为试验系统简图,SRS机械臂安装在气浮台上,机械臂重力由悬吊系统卸载,整个系统可以模拟空间微重力环境.OSE′EW为SRS机械臂,O-xyz为机械臂的基坐标系,z轴指向安装平面的法线方向,y轴竖直向上.

图6 试验系统示意图Fig.6 The Schematic diagram of experiment
试验中末端初始位置和欧拉角为[-557 -75 2 270]T、[90° 90° 0°]T,目标位置和欧拉角为[243 -118 2 289]T、[90° 90° 0]T.试验通过本文提出的逆运动学方法求解出机械臂运动至目标点的关节角,采用梯形速度插值方法规划关节运动,运动时间共122 s,其中加速阶段为10 s,减速阶段30 s.机械臂位于初始位置的臂型角为0.095 rad,运动至目标点的臂型角设置为0 rad.
试验的关节曲线变化如图7所示,各关节曲线连续平滑,机械臂运动稳定.图8为末端的位置变化曲线,在86 s接近肩关节奇异位形.图9为臂型角的变化曲线,臂型角从初始0.095 rad减小至0 rad.图10对比了两种方法在竖直方向的空间位移,采用文献[10]提出的关节角参数化方法时肘关节在竖直方向最大位移为170 mm,采用本文提出的求解方法时最大位移为60 mm.因此本文提出的逆运动学求解方法可以减小机械臂肘部在重力方向上的位移,更适合操作空间受限的试验系统中.
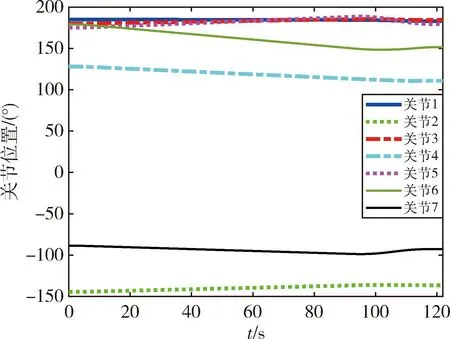
图7 试验关节位置变化曲线Fig.7 Changes in the joint position of experiment
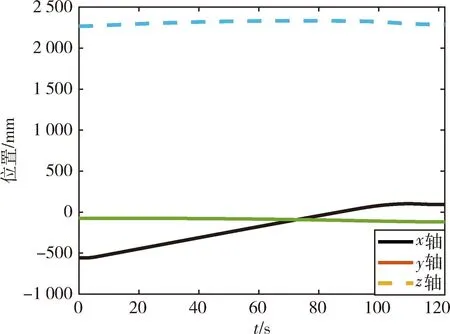
图8 试验的末端位置变化Fig.8 Changes in the end position of experiment
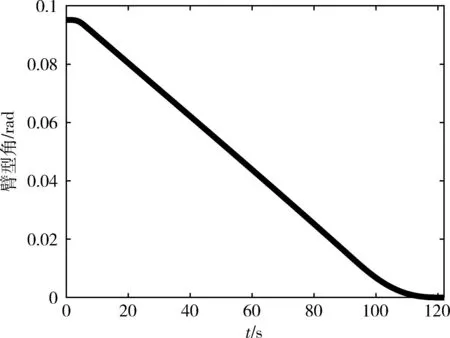
图9 试验臂型角变化曲线Fig.9 Changes in the arm-angle of experiment
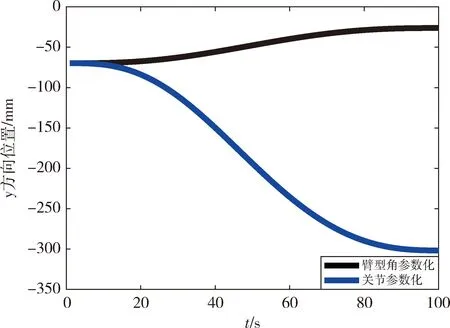
图10 不同逆运动求解方法下的y方向肘部位移Fig.10 The elbow positions of y direction under different inverse kinematics solution
4 结 论
针对SRS结构的机械臂,本文提出了一种基于臂型角的逆运动学求解方法. 根据目标位置构建臂型角,当臂型角非奇异时,利用SRS机械臂的几何特征求出逆运动学解析解. 当臂型角奇异时,利用肘关节位置约束求出逆运动学解析解.
在UG-Simulink联合仿真中,机械臂有效通过了笛卡尔空间内包含肩关节奇异点的直线路径. 在物理试验中,采用梯形速度插值方法规划关节空间运动,完成了通过奇异点的空间抓捕和释放操作. 对比本文方法和已有关节角参数化方法,本文方法在操作面外空间构型的位移量减小50%以上.
仿真和试验结果表明提出的逆运动学算法能有效解决SRS机械臂肩关节存在奇异点时的多解问题,更适应于运动空间受限时的七自由度机械臂运动控制.
