挠性航天器的自耦PD姿态控制方法
2024-03-12黄利容曾喆昭
黄利容, 曾喆昭, 曾 鹏
长沙理工大学,长沙 410076
0 引 言
随着航天重大工程的逐步实施,现代航天器通常需要搭载多种挠性附件[1],如太阳能电池板和大型天线等.然而,由于姿态控制系统中存在外部干扰,挠性附件会带来严重的振动问题,从而影响姿态控制的效果.随着航天器在空间领域的广泛应用,对姿态的控制精度要求也越来越高,因此,保持航天器的高精度姿态控制且能够有效抑制挠性附件的振动仍然具有很大的挑战性[2].
近年来,国内外学者们对于航天器的姿态控制提出了许多有效的控制方法.文献[3]考虑到航天器系统参数的不确定性,提出了一种可以在线更新定律的自适应鲁棒控制器,有着较好的增益鲁棒性.文献[4]设计了一种与模型无关的无量纲级联姿态反馈自抗扰控制器,在航天器存在参数不确定性以及外部干扰的情况下依旧可以取得有效的控制.文献[5]研究参数不确定挠性航天器的T-S模糊模型,并结合并行分布式补偿技术设计了非线性模糊控制器,取得了良好的控制效果.文献[6]基于终端滑模控制提出了一种具有有限时间内收敛的自适应控制方法,有效提高了系统的响应速度以及抗干扰能力.文献[7]将线性矩阵不等式与凸优化算法结合,设计了鲁棒输出反馈控制器,实现了航天器姿态的稳定控制.文献[8]设计了一种自适应双闭环姿态控制器,通过引入一个虚拟有界的角速度,将姿态控制问题降阶为角速度控制问题.文献[9]结合变结构控制策略和范数自适应估计算法设计了自适应鲁棒容错控制器,对存在参数不确定性以及执行器部分失效的航天器取得了有效的姿态控制.文献[10]采用预设性能方法设计航天器的姿态控制器,可以保证控制过程的暂态响应,并引入强化学习算法以解决航天器的惯量不确定性问题.文献[11]提出了鲁棒模型预测姿态控制方法,可将实际的航天器系统驱使到预设的以标称轨迹为中心的“管道”不变集内,并沿着标称轨迹到达平衡点,实现了在外部扰动下航天器姿态角的快速控制.文献[12]通过将神经网络和障碍李雅普诺夫函数结合来处理航天器模型参数的不确定性以及未知扰动,然后根据反步法设计了鲁棒自适应姿态控制器.然而上述方法皆属于集中控制,仅仅通过姿态控制器去抑制挠性附件的振动难以取得令人满意的效果,因此须引入主动振动控制器抑制挠性附件的振动,以此来取得更好的控制效果[13].
对于主动振动控制器的设计,文献[13]采用了预设性能控制(prescribed performance control,PPC)方法,该方法通过预先定义的性能函数和误差变换,使得闭环系统的收敛速度、超调量和稳态误差保持在预定范围内,可以获得预期的抑制效果.文献[14]设计了多模态正位置反馈主动振动控制器,有效提高了挠性附件的阻尼,从而提高了航天器系统的稳定性.文献[15]首次提出了一种结构较为简单的全自适应分量合成振动抑制(fully adaptive component synthesis vibration suppression,FACSVS)控制方法,该方法计算量较小并对振动频率的不确定性具有较好的鲁棒性.文献[16]设计了全阶滑模主动振动控制器有效减少挠性附件的振动,从而使得挠性振动模态在有限时间内快速衰减.
然而航天器是一个多输入多输出的系统,挠性结构与航天器主体之间又具有较强的耦合,导致现有的姿态控制器以及主动振动控制器结构复杂且存在大量矩阵的运算,不利于工程实际,因此在考虑外部干扰和模型参数不确定性的情况下,既可以保持高性能的姿态控制和强鲁棒性的主动振动控制,又能优化控制器结构的方法有待进一步研究.曾喆昭教授[17-18]为此提出一类新型的控制理论,即自耦PID(ACPID)控制理论.ACPID控制理论方法的主要优势如下:
1)ACPID控制器不仅保留了传统PID控制器简单的优势,且P、I和D这3个环节只由一个速度因子统一驱动,因而只需镇定一个速度因子;
2) 由过渡过程时间tr来镇定速度因子,简单实用:① ACPID的速度因子镇定规则:zc=10α/tr,1<α≤10;②ACPD与ACPI的速度因子镇定规则:zc=20α/tr,1<α≤10;
3)ACPID、ACPD与ACPI控制系统都是临界阻尼系统,因而都具有良好的鲁棒稳定性和动态响应特性;
4)ACPID控制理论将已知或未知动态及其不确定性以及外部有界扰动等一切复杂因素定义为一个总扰动,则可将复杂非线性系统等价映射为线性扰动系统[19-21],淡化了线性与非线性系统分类的概念.
本文的主要贡献在于将ACPID控制理论应用于挠性航天器系统,分别设计了ACPD姿态控制器与ACPD主动振动控制器,取得了良好的控制效果:在面临外部干扰以及模型参数不确定的情况下可以取得航天器姿态的高精度控制,并能使挠性附件的振动快速衰减.
1 挠性航天器的数学模型
1.1 系统描述
根据文献[22],受到外部干扰情况下挠性航天器的动力学模型可表示如下:
(1)
(2)
式中,ω=[ω1ω2ω3]T为航天器相对惯性坐标系的姿态角速度,J∈R3×3为航天器的转动惯量矩阵,u=[u1u2u3]T为控制输入力矩,d∈R3×1为外部干扰力矩,考虑具有五阶挠性模态的情况,则柔性附件的模态坐标向量η=[η1η2η3η4η5]T,δ∈R5×3为航天器刚体与柔性附件的耦合矩阵,C=2ξΩ为阻尼矩阵,K=Ω2为刚度矩阵,ξ和Ω分别为振动模态的阻尼比和自然频率,δa∈R5×5为压电作动器与柔性附件的耦合矩阵,up=[up1up2up3up4up5]T为压电作动器的输入电压.对于任意三维向量ν=[ν1ν2ν3]T,ν×表示反对称矩阵
本文采用修正的罗德里格斯参数(modified rodrigues parameters,MRP) 来描述航天器的姿态角,MRP定义为σ=φtan(φ/4)=[σ1σ2σ3]T∈R3×1,其中,φ∈R3×1表示为欧拉主轴向量,φ表示为欧拉旋转角,σi(i=1,2,3)表示为MRP每个轴的姿态角.则航天器的姿态运动学方程[16]为
(3)
其中,G(σ)=0.25[(1-σTσ)I3+2σσT+2σ×],I3为3×3单位矩阵.
结合式(1)、(2)和(3)可得受外部扰动下的挠性航天器系统为
(4)
1.2 系统映射
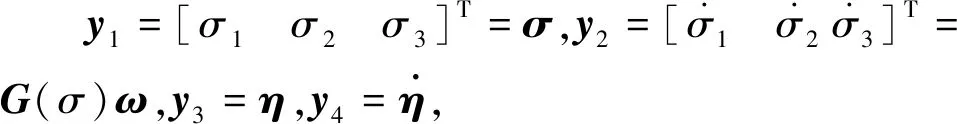
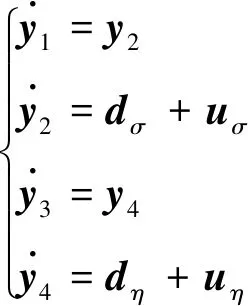
(5)
式中,uσ、uη为虚拟控制力,uσ=[uσ1uσ2uσ3]T=G(σ)J-1u,uη=[uη1uη2uη3uη4uη5]T=-δaup.
2 ACPD控制系统设计
2.1 ACPD虚拟控制器设计

(6)
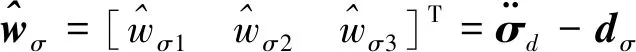
根据ACPID控制理论思想[17-18]可得ACPD姿态控制器的控制力矩为
(7)
u=JG-1(σ)uσ
(8)
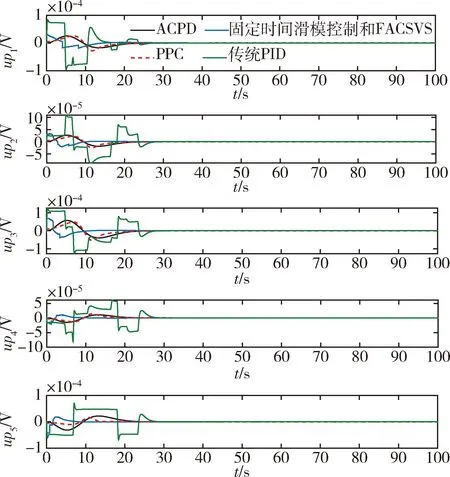
其中,|ui|≤uim(i=1,2,3),uim为控制力矩ui的最大幅值,zσ=zσI3,0 (9) 根据ACPID控制理论思想[17-18]可得ACPD主动振动控制器的控制电压为 (10) (11) 其中,zη=zηI5,0 证明.将式(7)代入受控误差系统(6),可得子控制系统为 (12) (13) 由式(13)可得系统传递函数为 (14) 当0 由式(14)可得系统的单位冲激响应为 hσi(t)=texp(-zσt)ε(t) (15) 由式(15)可得受控误差系统的时域形式为 (16) 其中,“*”表示卷积积分运算. (17) 由式(15)可知,当0≤t<∞时,hσi(t)≥0,且hσi(∞)=0,因而有 (18) 将式(18)代入式(17),可得稳态误差为 (19) 外部扰动是总扰动的一部分,在总扰动有界情况下,由式(19)可知:增加速度因子可以显著降低稳态误差,提高抗扰动能力,因而ACPD姿态控制系统具有良好的抗扰动鲁棒性,证毕. 定理2的证明参照定理1,此处不再赘述. 由定理1与定理2可知,当速度因子大于0时,ACPD姿态控制系统和ACPD主动振动控制系统都是鲁棒稳定的,且速度因子越大,控制系统的稳态精度则越高,抗扰动能力则越强,否则反之.然而,在启动控制初期,速度因子过大,则会导致控制力过大而出现超调现象.因此为防止姿态控制出现超调现象,在基于文献[20]的基础上使用自适应速度因子模型.主动控制器则需要更大的速度因子来有效抑制挠性附件的振动,则本文选择的速度因子模型如下所示: (20) zη=20α2/tη (21) 其中,1<α≤10,tσ、tη是由动态过程进入稳态过程的过渡过程时间. 将本文的ACPD姿态控制器与ACPD主动振动控制器应用于挠性航天器系统,为了验证本文控制方法的有效性,进行仿真试验和分析,并与文献[13]和文献[15]所提出的方法进行比较分析. 仿真试验中,角速度的初值为ω(0)=[0 0 0]T,MRP的初始值为σ(0)=[0.038 9 0.056 0 -0.038 9]T,MRP的期望值为σd=[0 0 0]T,挠性模态的初始值为η(0)=[0 0 0 0 0]T.挠性航天器系统的参数选自文献[13],其具体数值如表1所示,姿态控制力矩的最大值为uim=50 N·m,挠性控制电压的最大值为0.01 V. 表1 仿真参数Tab.1 Simulation parameters 假设挠性航天器在高度500 km的轨道上运行,则外部干扰包括干扰力矩、大气干扰和其他环境干扰,如下所示[13]: d=0.01× 其中,Ω1=Ω(1,1),Ω2=Ω(2,2),Ω3=Ω(3,3). ACPD控制方法、文献[13]以及文献[15]控制方法的控制器结构如下: (1)ACPD姿态控制器与ACPD主动振动控制器结构 (22) (23) (2)文献[13]固定时间滑模姿态控制器与FACSVS主动振动控制器结构 (24) (25) (3)文献[15]PPC姿态控制器与PPC主动振动控制器结构 (26) (27) 表2 3种控制器的控制参数Tab.2 Control Parameters of Three Controllers 将3种控制方法应用于挠性航天器,其仿真结果如图1~5所示,显然3种控制方法都能实现挠性航天器的有效控制.在ACPD控制方法下,挠性航天器的姿态角和角速度的收敛时间约为20 s,需要的最大力矩为34 N·m,其五阶挠性振动模态的最大值分别为8.3×10-4、1.7×10-4、4.5×10-4、1.5×10-4和3.7×10-4,衰减时间约为20 s;在固定时间滑模控制和FACSVS主动振动控制下,挠性航天器的姿态角和角速度的收敛时间约为30 s,需要的最大力矩为50 N·m,其五阶挠性振动模态的最大值分别为1.6×10-2、3.4×10-3、5.4×10-3、1×10-3和1.9×10-3,衰减时间约为30 s;在PPC方法下,挠性航天器的姿态角和角速度的收敛时间约为25 s,需要的最大力矩为36 N·m,其五阶挠性振动模态的最大值分别为9.2×10-4、2.6×10-4、8.8×10-4、2.3×10-4和1×10-3,衰减时间约为20 s;在PID控制方法下,挠性航天器的姿态角和角速度的收敛时间约为28 s,需要的最大力矩为50 N·m,其五阶挠性振动模态的最大值分别为9.4×10-4、4.1×10-4、4.6×10-4、4.4×10-4和3.8×10-4,衰减时间约为25 s. 图1 姿态角变化曲线Fig.1 The response of attitude angular 图2 角速度变化曲线Fig.2 The response of angular velocity 图3 控制力矩变化曲线Fig.3 The response of control torque 图4 模态坐标变化曲线Fig.4 The response of modal coordinate 图5 控制电压变化曲线Fig.5 The response of input voltage 不同控制方法的控制精度如表3所示,结合图1~5可知,本文所提出的ACPD控制方法,能有效抑制挠性附件的振动,使得姿态角以及角速度更快收敛,且具有更高的控制精度. 表3 不同控制方法的稳态精度Tab.3 Steady-state accuracy of different control methods 为了进一步验证本文所提出的ACPD控制方法的鲁棒性,保持本文控制器的参数不变,考虑航天器的转动惯量矩阵J、刚体与柔性附件的耦合矩阵δ以及自然频率Ω存在偏差,失配程度如表4所示.姿态角σ1的控制结果如图6所示,挠性模态η1的控制结果如图7所示. 图6 姿态角σ1变化曲线Fig.6 The response of MRPs σ1 图7 模态坐标η1变化曲线Fig.7 The response of modal coordinate η1 表4 参数失配程度Tab.4 Parameter mismatch degree 由图6可知,试验1和试验4的姿态控制效果基本一致,试验2和试验3的姿态角σ1控制效果基本一致,可以看出参数δ以及Ω基本不影响姿态控制效果;由图7可知,试验2和试验3的挠性模态η1控制效果基本一致,可以看出参数Ω基本不影响挠性模态控制效果,4组试验控制下,姿态角σ1的控制精度均为1×10-6,挠性模态η1的控制精度均为1×10-7数量级.以上分析表明了ACPD控制方法具有良好的鲁棒性. 针对挠性航天器的控制问题,本文基于ACPID控制理论分别设计了ACPD姿态控制器与ACPD主动振动控制器.仿真结果表明本文控制方法的有效性,在带有外部扰动以及模型不确定性的情况下,可以取得良好的控制性能:响应速度快、控制精度高和鲁棒性强.本文控制方法的突出优势是控制系统结构简单,计算量小,仅涉及2个速度因子的镇定,而且通过过渡过程时间tσ和tη来镇定速度因子,因而简单实用.文献[13]和文献[15]的控制方法涉及更多的矩阵运算,导致控制器结构复杂,计算量大并且需要镇定的参数过多,因而本文提出的ACPD控制方法更便于工程实际.2.2 ACPD主动振动控制器设计
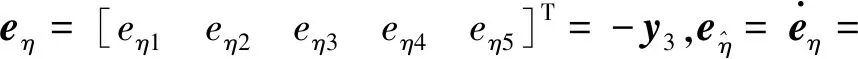
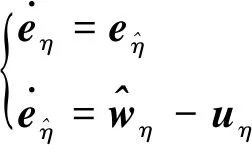

2.3 控制系统分析


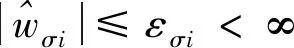
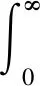
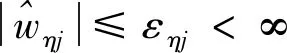
2.4 速度因子镇定
3 仿真分析

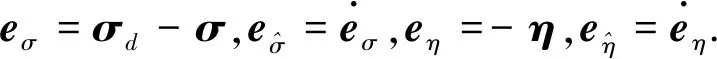
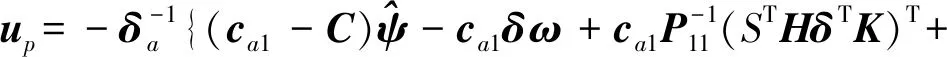

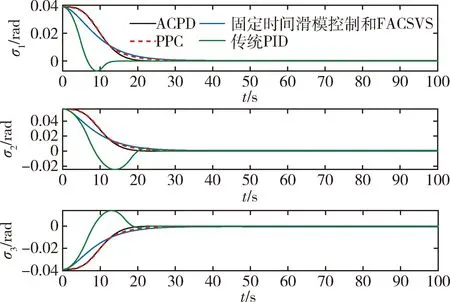
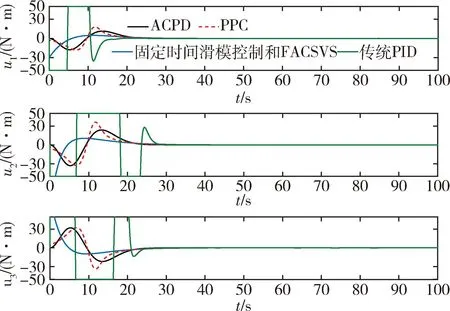
3.1 控制器对比分析仿真试验

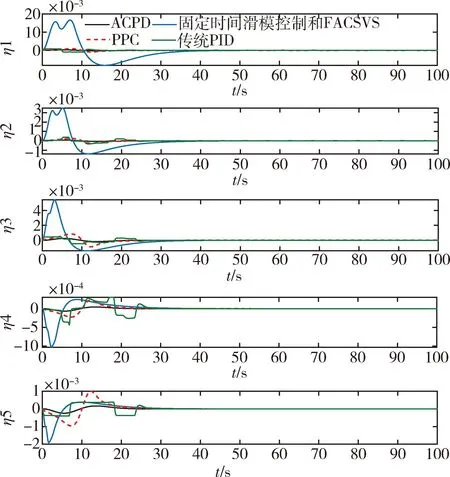

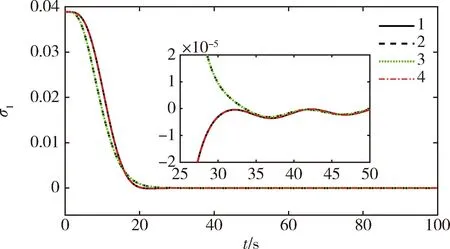
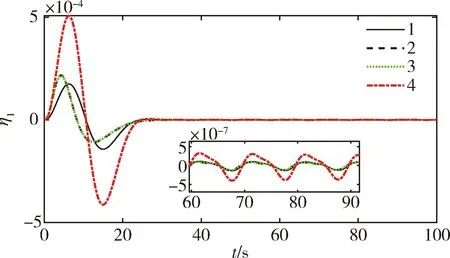
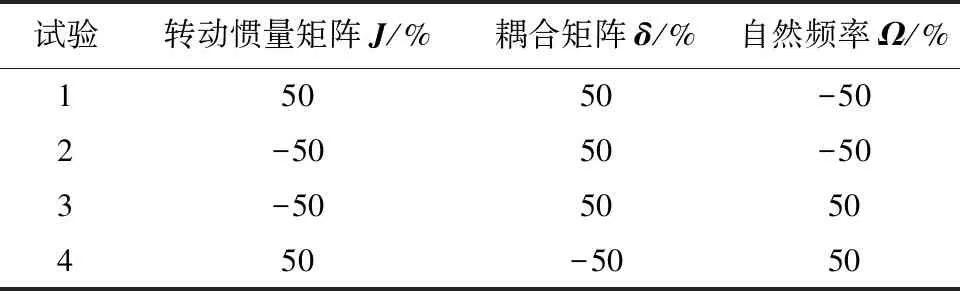
3.2 鲁棒性分析仿真试验
4 结 论
