一种基于虚拟星敏感器的卫星姿态确定方法

张志方, 林瀚峥, 李公军

1. 北京控制工程研究所, 北京 100094

2. 空间智能控制技术全国重点实验室, 北京 100094

0 引 言

对于配置了星敏感器和陀螺的卫星,普遍采用基于星敏感器和陀螺的卡尔曼滤波方法确定卫星姿态[1].文献[2]将一种自适应强跟踪滤波算法应用于卫星姿态确定中,兼顾精度和鲁棒性.文献[3]设计了基于无迹卡尔曼滤波的星敏感器和陀螺组合定姿算法,提高了定姿精度.文献[2-3]以及文献[4-12]中滤波方法的增益矩阵及误差方差矩阵需要实时递推计算,其计算量均较大.

定常增益卡尔曼滤波(constant gain Kalman filtering,CGKF)是用常值增益矩阵代替卡尔曼滤波增益矩阵的递推计算,不需要实时计算误差方差矩阵以及滤波增益矩阵,大幅减小了计算量,适合星载计算机在轨实时计算,文献[13-15]对此进行了论述,文献[13]给出了定常增益卡尔曼滤波器的设计方法,并给出了观测方程的具体形式.从定常增益矩阵的求解可知,它与星敏感器的安装矩阵相关,而且分为单星敏定姿和双星敏定姿两种形式,不同的星敏感器参与定姿时均需要设计相应的定常增益矩阵,对于配置3个或3个以下星敏感器的卫星,定常增益矩阵个数及滤波器的复杂度尚可接受,对于配置更多星敏感器的大型航天器,则存在滤波器定常增益矩阵过多、系统复杂的问题.

本文在简化滤波器设计、减少定常增益矩阵方面进行了研究,提出了一种基于虚拟星敏感器的姿态确定方法,统一了滤波器定常增益矩阵,节省了星载计算机资源对工程应用具有重要意义.

1 定常增益卡尔曼滤波方法

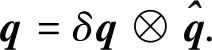
(1)

由卫星的姿态运动学方程可以建立如下状态估计误差方程:

(2)

式中,F(t)为状态转移矩阵,w(t)为系统噪声.在时间区间[tk-1,tk]上,离散化的状态方程为

ΔXk=Φk/k-1ΔXk-1+Wk-1

(3)

式中,Φk/k-1为tk-1时刻至tk时刻的一步转移阵,Wk-1为系统激励噪声序列(零均值的白噪声随机序列).

滤波器观测方程为

ΔZk=HkΔXk+Vk

(4)

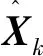
状态一步预测

(5)

状态估计

(6)

滤波增益矩阵计算

(7)

一步预测均方误差

(8)

估计均方误差

Pk=(I-KkHk)Pk/k-1

(9)

式中,Qk为系统噪声序列的方差阵,Rk为量测噪声序列的方差阵.按文献[13]设计观测方程,采用单星敏感器定姿时,量测阵H为

(10)

采用两个星敏感器定姿时,量测阵H为

(11)

式中,XB、YB、ZB、XB,A、YB,A、XB,B和YB,B为星敏感器的安装矢量,Hk、Qk和Rk为常值矩阵,稳态飞行时Φk/k-1也近似为常值,矩阵Pk在稳态时收敛于定常矩阵P0,滤波增益矩阵Kk在稳态时也将收敛于定常矩阵K0.由以上确定出的定常增益矩阵K0不需要实时计算,省去了计算矩阵Pk/k-1、Pk及Kk,既节省了计算时间,又保证了滤波系统的稳定性,定常增益卡尔曼滤波广泛应用于星敏感器和陀螺的姿态确定系统中.

从式(7)、(10)和(11)可以看出,增益矩阵K与量测阵H相关,而量测阵H与星敏感器安装矩阵相关,即采用不同的星敏感器定姿时定常增益矩阵不同.以配置3个星敏感器的卫星为例,对地定向时需要6个定常增益矩阵,使用的定姿星敏分别对应星敏1、星敏2、星敏3、星敏1和2、星敏1和3及星敏2和3.如果卫星还设计了惯性定向飞行模式,由于此时的Φk/k-1不同,因此还需要再增加6个定常增益矩阵.对于常规卫星,一般配置2～3个星敏,定常增益矩阵一般不超过12个,数量尚可接受,但对于由多个舱段组成的大型航天器,星敏感器总数可能多达10个,定常增益矩阵的个数N最多有110个.

(12)

其中k为星敏个数,每一个定常增益矩阵都是6行4列的矩阵,110个增益矩阵一共有2 640个参数,每个参数都有可能需要在轨修改,这对星载计算机有限的存储、计算资源来说无疑是巨大的负担,因此需要寻找简便的方法来实现多星敏感器定姿,减少常增益矩阵,简化滤波器设计,本文提出一种基于虚拟星敏感器的滤波方法来解决该问题.

2 基于虚拟星敏感器的姿态确定方法

由上节分析可知,导致定常增益矩阵过多的原因是量测阵H与星敏感器的安装矩阵相关,而不同的星敏感器的安装矩阵不同.基于虚拟星敏定姿的核心思想是构造虚拟星敏,该虚拟星敏的安装矩阵固定且唯一,为计算简便,虚拟星敏的测量系与卫星本体系重合,虚拟星敏的光轴矢量与星体X轴平行,横轴矢量与星体的X轴平行,安装矩阵为单位阵.基于虚拟星敏定姿的定常增益矩阵与星敏感器的实际安装矩阵无关,与固定且唯一的虚拟星敏安装矩阵相关.当卫星有对地定向飞行和惯性定向飞行两种模式时,定常增益矩阵仅为两个.

基于虚拟星敏定姿分为3步:1)星敏感器数据预处理,将所有星敏的测量数据统一到当前星时;2)统一测量基准,完成星敏感器相对基准标定[17-20];3)构造虚拟星敏的输出数据,基于虚拟星敏定姿.

2.1 统一星敏感器输出数据时间

对所有有效的星敏感器测量数据进行预处理,将测量数据的时间补齐,进行时间滞后补偿、光行差补偿等,将各星敏感器的测量数据统一转换到当前星时下的输出,方便后续使用统一时间基准的输出数据.下面给出一种计算量小的时间滞后补偿及光行差补偿算法.

若星敏感器i的输出为四元素q,记

q=[q1q2q3q4]T

其中q4为标量.若星敏感器i的输出为光轴矢量ZI,m和横轴矢量XI,m,则由光轴矢量和横轴矢量转换得到四元素q,计算过程如下:

首先计算星敏感器i测量系相对惯性系的方向余弦矩阵

(13)

再由CSI得到四元素q.

由四元素q及星体姿态角速度ωS进行时间补偿计算

(14)

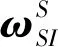
根据卫星姿态运动学方程有

(15)

其中,

(16)

(17)

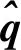
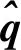
(18)

(19)

记光行差补偿量γ=[γxγyγz]T

(20)

式中,vx、vy和vz为卫星在赤道惯性系的速度,c为常值299 792.458.光行差补偿计算公式如下(同时完成归一化和正交化):

光轴矢量补偿及归一化

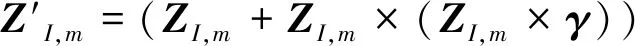
横轴矢量补偿及归一化

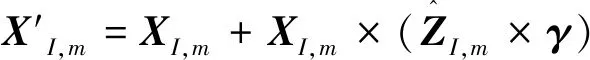
叉乘求Y矢量并归一化

叉乘求横轴矢量并归一化

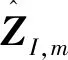
2.2 统一星敏感器测量基准

为了统一星敏感器的测量基准,以下给出一种适合星载计算机在轨实时计算的星敏感器相对基准标定方法,其标定原理为:根据同一时刻,各个星敏感器的输出数据和安装矩阵确定的卫星本体相对惯性系的姿态矩阵相等,由此等式以一个星敏感器的理论安装矩阵修正另一个星敏感器的理论安装矩阵.

在进行星敏感器相对基准标定之前,先按上节所述完成星敏感器测量数据的时间滞后补偿和光行差补偿,并完成光轴矢量和横轴矢量的正交化和归一化.下面以星敏感器1为标定基准,进行星敏感器2的相对基准在轨标定算法描述.

由星敏感器的光轴矢量和横轴矢量,得到星敏感器1当前星时(t时刻)的输出CS1I和星敏感器2当前星时的输出CS2I

(21)

设星敏感器2的理论安装矩阵与以星敏感器1为基准进行标定后的安装矩阵之间误差矩阵为CΔ,记标定后的星敏感器2的安装矩阵为CS2B,且

根据星敏感器2的t时刻的输出CS2I和星敏感器2标定后的安装矩阵CS2B,可得t时刻星体相对惯性系的姿态矩阵

(22)

由于相同测量基准得到的同一时刻的星体相对惯性系姿态矩阵相等,即C1BI=C2BI,则有

(23)

由此可得

(24)

一般标定误差角为小量,记标定误差角为δx、δy和δz,3-1-2转序下CΔ近似为

(25)

由式(24)和(25)可反解得到标定误差角δx、δy和δz,考虑到星敏感器测量噪声的影响,对标定误差角δx、δy和δz进行滤波,滤波形式如下:

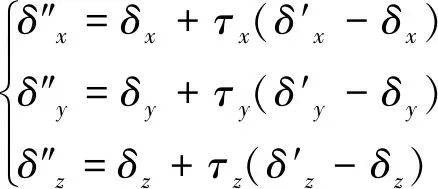
(26)

(27)

式中,RZ、RX和RY分别表示绕星体Z轴、X轴和Y轴旋转所得的方向余弦矩阵,CΔ2为星敏2的安装误差矩阵.

以星敏感器1为基准,标定后的星敏感器2的安装矩阵为

(28)

同理以星敏感器1为基准标定其他星敏,得到其他星敏标定后的安装矩阵.

通过相对基准标定,实现所有星敏感器的测量基准统一.一般选择结构稳定性较好的星敏感器作为基准星敏,其他星敏感器以它为基准进行标定.

2.3 基于虚拟星敏定姿

为了简化计算,将虚拟星敏感器的测量系设计为与卫星本体系重合,即虚拟星敏感器的安装阵为单位阵.

虚拟星敏感器的构造分为基于单星敏感器构造和基于双星敏感器构造两种方式:

(1)基于单星敏感器输出构造虚拟星敏输出

(29)

结合星敏感器的安装矩阵CSB(已经过相对基准标定后的安装矩阵),可得由此星敏感器计算得到的本体系相对惯性系的姿态矩阵

(30)

记

则由单星敏输出数据构造的虚拟星敏的光轴矢量和横轴矢量分别为ZIV和XIV.

(2)基于双星敏感器输出构造虚拟星敏输出

光轴矢量叉乘求横轴矢量并归一化

光轴矢量与横轴矢量叉乘求Y矢量并归一化

ZIA、XIA和YIA即为由星敏1和星敏2的光轴矢量构造出来的转换星敏的输出,则该星敏的测量系相对惯性系的姿态矩阵为

(31)

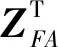
(32)

可得转换星敏的安装矩阵为

(33)

由转换星敏的输出以及安装矩阵可得本体系相对惯性系的姿态矩阵

(34)

同理可得由双星敏输出数据构造的虚拟星敏的光轴矢量ZIV和横轴矢量XIV.

不论是使用单星敏的输出数据还是双星敏的输出数据,得到的虚拟星敏的光轴矢量ZIV和横轴矢量XIV仅一套,虚拟星敏的安装矩阵为单位阵,且固定不变,因此只需设计基于单星敏的定常增益卡尔曼滤波,不再需要设计基于双星敏的定常增益卡尔曼滤波,具体设计方法参见文献[13],可得到基于虚拟星敏的卡尔曼滤波稳态定常增益矩阵.

由于虚拟星敏感器的安装矩阵唯一,进行滤波器设计时仅与该安装矩阵相关,大幅简化了多星敏感器滤波修正逻辑,简化了滤波器设计,降低了软件的复杂度,提高了系统的可靠性.

与常规的定常增益卡尔曼滤波方法相比,单星敏定姿时使用的均为该星敏的光轴矢量和横轴矢量,双星敏定姿时使用的均为两个星敏的光轴矢量,从信息利用角度来看,两种方法没有本质的区别.本文所述的方法对星敏感器的个数没有限制,同样适用于配置3个以下星敏感器的卫星.

3 仿真实例

针对某卫星进行星敏感器及陀螺的姿态确定仿真验证,包括相对基准标定、采用常规的CGKF方法进行姿态确定、基于虚拟星敏定姿.仿真中星敏感器光轴测量误差为5″,横轴测量误差为35″.

(1)星敏相对基准标定

以星敏感器1为基准,标定星敏感器2的安装误差.设置星敏感器2的安装误差角x为0.05°,安装误差角y为0.1°,安装误差角z为-0.1°.仿真结果表明,20 min内三轴安装误差即达到稳态,收敛到真值,如图1所示.

图1 星敏感器相对基准标定误差角Fig.1 Star sensor calibration error angle relative to reference

由以上仿真可以看出,使用CGKF时,三轴定姿误差均小于0.002°,且双星敏定姿与单星敏定姿切换过程平滑,无明显姿态波动.

(2)常规的CGKF定姿

使用CGKF方法,使用单星敏(星敏2)定姿时,定姿误差如图2所示,使用CGKF,使用双星敏(星敏1和星敏2)定姿时,定姿误差如图3所示.

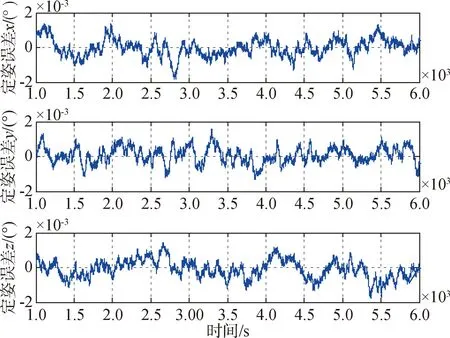
图2 单星敏定姿误差(CGKF)Fig.2 Attitude determination error using single star sensor(CGKF)

图3 双星敏定姿误差(CGKF)Fig.3 Attitude determination error using dual star sensors(CGKF)

使用CGKF方法,由双星敏(星敏1和星敏2)定姿切换到单星敏定姿(星敏1),12 000 s时刻切换,定姿误差如图4所示.

图4 星敏切换期间定姿误差(CGKF)Fig.4 Attitude determination error during the switching period of star sensors(CGKF)

(3)基于虚拟星敏定姿

基于虚拟星敏定姿,使用统一的滤波增益矩阵.使用单星敏(星敏2)定姿,定姿误差如图5所示.

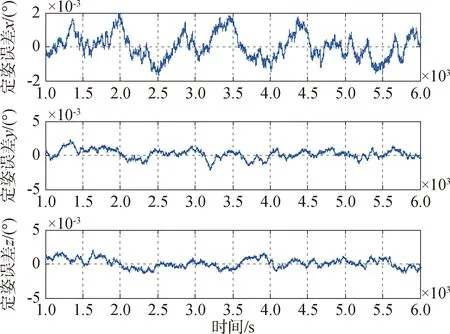
图5 单星敏定姿误差(基于虚拟星敏定姿)Fig.5 Attitude determination error using single star sensor (attitude determination based on virtual star sensor)

基于虚拟星敏定姿,使用双星敏(星敏1和星敏2)定姿,定姿误差如图6所示.

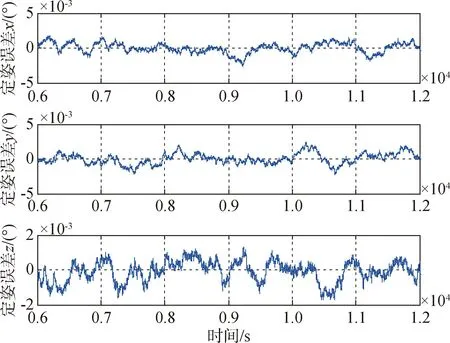
图6 双星敏定姿误差(基于虚拟星敏定姿)Fig.6 Attitude determination error using dual star sensors(attitude determination based on virtual star sensor)

基于虚拟星敏定姿,由双星敏(星敏1和星敏2)定姿切换到单星敏定姿(星敏1),12 000 s时刻切换定姿星敏,定姿误差如图7所示.

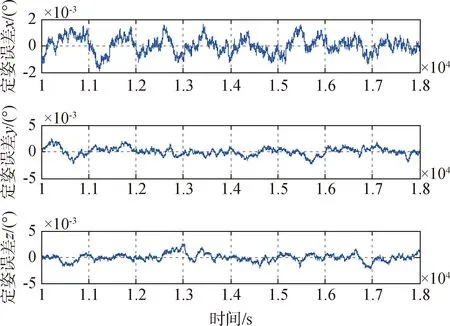
图7 星敏切换期间定姿误差(基于虚拟星敏定姿)Fig.7 Attitude determination error during the switching period of star sensors (attitude determination based on virtual star sensor)

由以上仿真可以看出,基于虚拟星敏定姿时,三轴定姿误差均小于0.002 2°,且双星敏定姿与单星敏定姿切换过程平滑,无明显姿态波动.

对比基于虚拟星敏定姿和常规的定常增益卡尔曼滤波两种仿真结果,在单星敏定姿、双星敏定姿以及定姿星敏切换过程中,两种方法定姿误差相当,均能达到10″以内,满足使用需求,仿真结果验证了基于虚拟星敏定姿方法的有效性.

4 结 论

本文针对配置多个星敏感器的卫星,采用CGKF方法进行姿态确定时定常增益矩阵过多的问题,提出了一种基于虚拟星敏感器的姿态确定方法.给出了一种计算量小、适合星载计算机在轨实时计算的星敏感器时间滞后补偿及相对基准标定算法,将虚拟星敏感器的测量系设计为与卫星本体系重合,基于单星敏/双星敏的输出数据构造虚拟星敏感器的输出数据,设计统一的滤波器定常增益矩阵进行姿态确定.通过数学仿真对比了本方法与常规的CGKF方法的姿态确定精度,两者相当.本方法统一了滤波器定常增益矩阵,简化了滤波器设计,节省了大量的星载计算机资源,不仅适用于配置多个星敏感器的卫星,同样适用于配置3个以下星敏感器的卫星,具有重要的工程应用价值.