基于ANCF的挠性太阳翼动力学建模及模态辨识研究

王慕昊, 舒通通, 魏鸿超, 赵亚涛, 夏 斌*

1. 中国星网网络创新研究院有限公司,北京 100029

2. 哈尔滨工业大学,哈尔滨 150001

0 引 言

太空飞行任务的多样化和规模化趋势,正推动着当前太空航天器结构朝着更大型和更具柔性化的方向发展[1-4].太阳能帆板、大型桁架、天线和大型机械臂等都是航天器实际应用中常见的典型大挠性附件[5-8],获取其动力学性能参数为航天器控制系统提供输入变得至关重要.10 m级的薄膜结构尚能进行地面真空试验,但目前大型薄膜结构展开尺度达到100 m,例如在地球静止轨道上使用2.4 GHz作为工作频率运行的红外通讯卫星,其薄膜结构直径需达到135 m[9].超大型太阳翼展开后的巨大尺寸成为限制其进行真空试验的首要因素,而不考虑空气阻尼测试获取的薄膜结构动力学性能参数与真实在轨参数具有很大差异,因此,进行精细化的动力学建模和在轨模态参数辨识研究变得至关重要.通过仿真模拟在轨航天器工况来获得更真实的模态参数,以评估薄膜结构的动力学性能,成为解决这一问题的有效途径之一[10].一些学者已经对含预应力可展薄膜结构进行了相关的动力学分析研究.胡宇[11]研究了薄膜阵面结构刚度影响因素,试验结果表明膜面振型与数值模拟结果基本吻合,但对应频率有较大差异,原因可能为试验条件未达到理想状态.邱慧等[12]在研究中对含薄膜和弹性索张拉系统的航天器平面结构的动力学特性进行了分析,并通过试验结果验证了湿模态仿真分析的准确性,从而推理出干模态仿真分析的一致性,并未进一步作干模态的试验验证.国际上的相关机构已经进行了与模态在轨辨识相关的试验验证工作,如美国针对直径8m的膜反射阵列天线的振动分析,利用双变量参数(two-variable-parameter,2-VP)膜模型和分布式传递函数法(distributed transfer function method,DTFM)预测天线面内应力的分布和振动模式,但忽略了空气阻尼对膜固有频率的影响[13].ZHANG等[14]基于温度-结构预应力导入方法,采用特征系统实现算法(eigensystem realization algorithm,ERA)对薄膜结构平面天线进行模态辨识,前两阶辨识准确率在5%以内.然而,上述相关研究多集中在试验或有限元模型,对于利用绝对节点坐标法进行含预紧张力的薄膜结构平面天线动力学建模与分析的报道较少.

本文基于应变-预应力导入方法,采用ANCF索梁模型和ANCF薄膜单元对某低轨卫星的太阳翼柔性附件开展动力学建模及分析,综合考虑了太阳光压力、气动阻力、重力梯度力矩和地磁力矩在内的复杂空间环境干扰,以高斯白噪声曲线加速度作为激励,施加于挠性结构连接处并获取薄膜结构的均布响应,基于输入输出数据,采用复模态指示函数法辨识薄膜复合结构的动力学参数.通过辨识结果与有限元模态分析结果对比分析,研究结果表明CMIF方法可有效地识别出薄膜复合结构的低阶固有模态,为该技术的工程实施提供了坚实的理论研究基础.

1 问题描述

1.1 结构组成

低轨卫星的挠性部件主要由太阳翼边框、太阳翼薄膜以及张力撑杆组成.星本体通过举升机构连接大面积太阳翼,太阳翼薄膜两侧对称布置张拉机构,太阳翼薄膜靠近刚性板的一端与刚性板布置有3处压板.太阳翼边框展开后,张力撑杆承受张拉机构的反作用力,有效降低边框的预应力水平.单侧太阳翼部件的具体约束形式见图1.挠性太阳翼的长宽比达5:1,卫星姿态机动过程中极易激发耦合振动,因此获取太阳翼部件动力学模态参数作为航天器控制系统的设计约束是必不可少的环节.

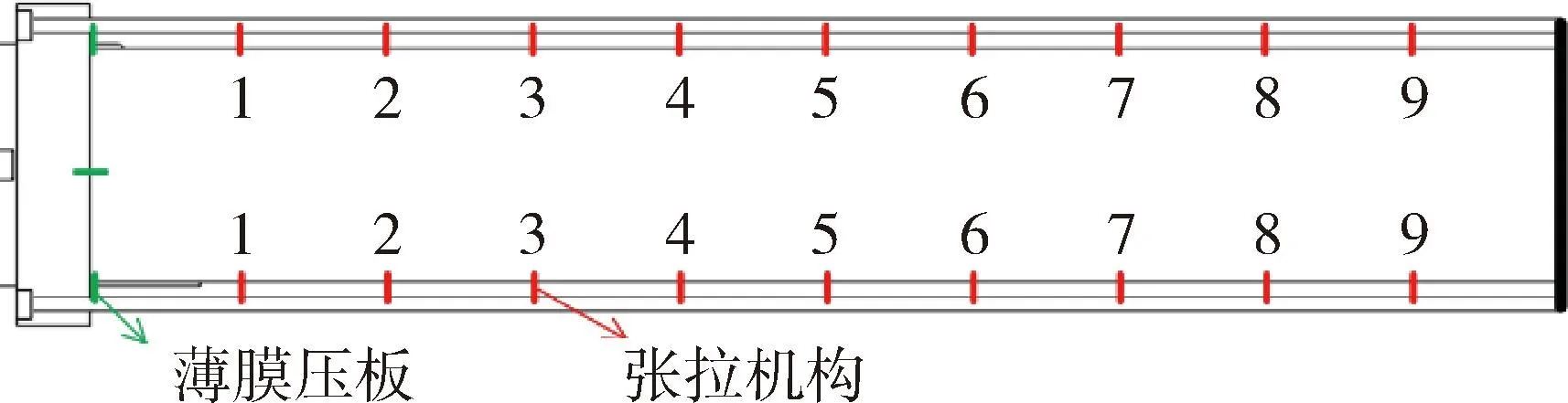
图1 单侧太阳翼部件约束示意图Fig.1 Constraints on one-sided solar wing components

1.2 材料属性

太阳翼边框采用碳纤维/环氧复合材料,截面形状及铺层设计参考文献[14].张力撑杆为铝合金材料,截面为管型.太阳翼薄膜采用聚酰亚胺树脂材料,厚度为0.4 mm.拉索为 2 mm圆截面凯夫拉纤维,设计张紧力20 N.

2 动力学模型及分析结果

2.1 ANCF索梁单元与壳单元

ANCF全参数梁单元可以描述梁截面的变形,适合于大截面梁的建模.但对于横截面很小、柔性较大的细长梁来说,截面变形不是关注的重点,从而可忽略沿截面方向的斜率矢量.这种节点坐标中忽略一个或几个方向斜率矢量的单元称作缩减单元,或称作梯度不足单元.

BERZERI等[15]首先提出了这种类型的平面缩减梁单元,GERSTMAYR等[16]将该单元推广为空间缩减梁单元(又称为索单元).利用ANCF索梁单元建立拉索的动力学模型,如图2所示.

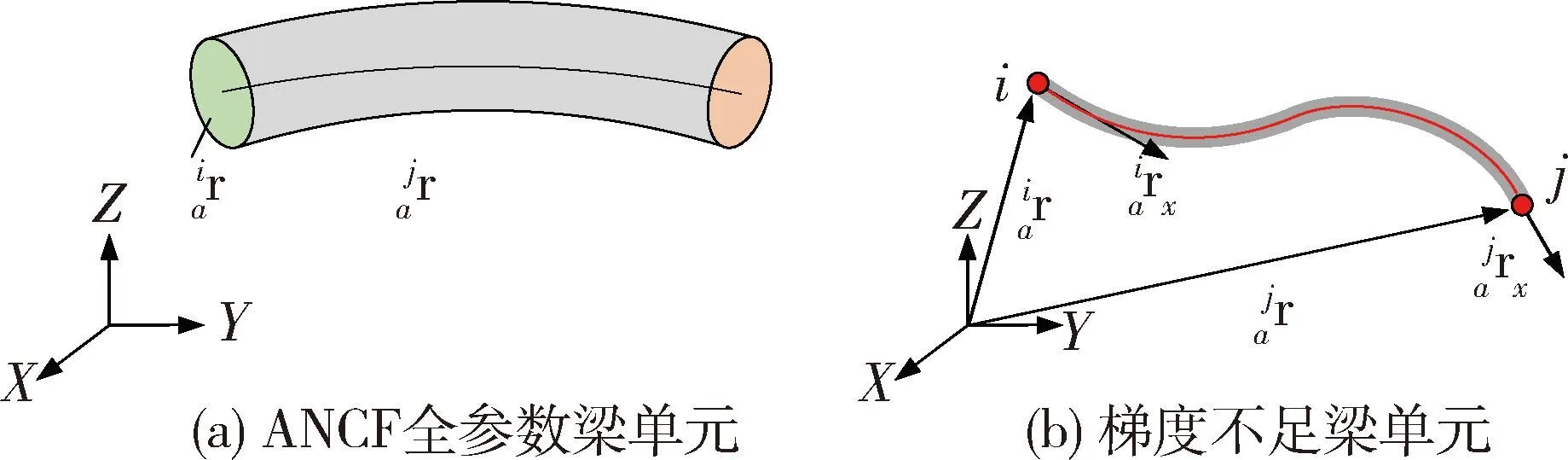
图2 空间缩减梁单元Fig.2 ANCF beam element

在绝对坐标系中,该单元中任意一点的位置可定义为

(1)

式中,S为3×12的形函数矩阵.单元的广义坐标可定义为

(2)

显然,该单元不能描述梁绕自身轴线的转动.对于ANCF缩减曲梁单元,其单元动能可写为

(3)

式中,单元的长度为L,ρ和A分别为索梁单元的密度和横截面积,M为单元的质量矩阵,矩阵中各项均为常数.

基于欧拉-伯努利梁理论,对于ANCF缩减曲梁单元,其应变能分为两部分:1)由中线的轴向变形引起;2)由弯曲变形引起,具体表达式为

(4)

式中,E为弹性模量,J为截面惯性矩,aε为轴向应变,aκ和aκ0分别为曲梁当前状态与初始状态的曲率.

如图3所示,基于参考文献[17]建立双线性剪切变形ANCF壳单元.

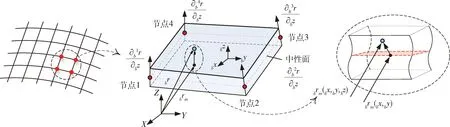
图3 双线性剪切变形ANCF壳单元Fig.3 ANCF shell element

薄膜单元通过网格划分,离散成一定数量的4节点单元,定义薄膜单元上任意物质点x的全局坐标br为

(5)

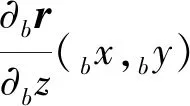
(6)

式中,向量bep、beg代表了单元上与节点全局位置和横向梯度相关的矢量.对于单元b上节点k有bkep=bkrk,bkeg=∂bkr/∂bz.则ANCF全局坐标表示为

br(bx,by,bz)=bS(bx,by,bz)be

(7)

形函数矩阵和节点全局坐标向量bS和be的表达式分别为

(8)

2.2 平衡方程

通过拉格朗日方程导出的薄膜结构系统动力学方程,具体形式为

(9)

式中,q为广义坐标,T为总动能,U为总弹性能,C(q,t)=0为约束方程,λ为约束方程对应的拉式乘子,Qf为外力的广义力.

拉索预紧力可通过定义ANCF索梁单元的单元长度L来实现.结构由于单元长度的变化,其应变为

ε=(L-L0)/L0

(10)

式中,L0为无应力状态下索梁单元的初始长度.

因此,给定单元参考长度L0,可以实现初始预应力的导入,同时在支撑边框、薄膜结构和张力撑杆等多重作用下维持初始状态的平衡.

2.3 边界条件

如图4所示,卫星包含4根太阳翼边框和2块太阳翼柔性基板,太阳翼边框编号为①～④,太阳翼柔性基板编号分别为A和B.

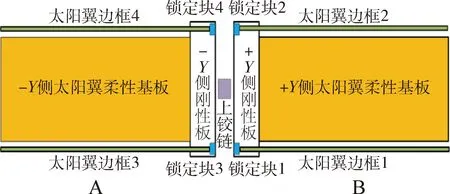
图4 柔性体布局Fig.4 Flex body layout

以+Y侧大挠性太阳翼装配体为例,简述柔性体建模过程.如图5所示,根据太阳翼几何包络尺寸抽取节点,其中每根太阳翼边框选取12个节点,共组成11个ANCF索梁单元.太阳翼A抽取11×3个节点,每4个节点按照顺时针顺序组成一个ANCF薄膜单元,共计20个单元.拉索处建立ANCF索梁单元.张力撑杆、拉索和边框等可展薄膜结构各个零件之间的连接采用耦合自由度的方式,以实现位移边界的协调.

2.4 分析结果

由表1材料特性及式(10)可计算出单元参考长度,该预载荷可实现膜面张紧.编号3_2～3_10的张力机构对应图6中1～9号拉索稳态拉力.基于薄膜结构的固支约束边界和张拉力,利用有限元软件可以计算出薄膜结构的主要频率和振型(前6阶见图7).

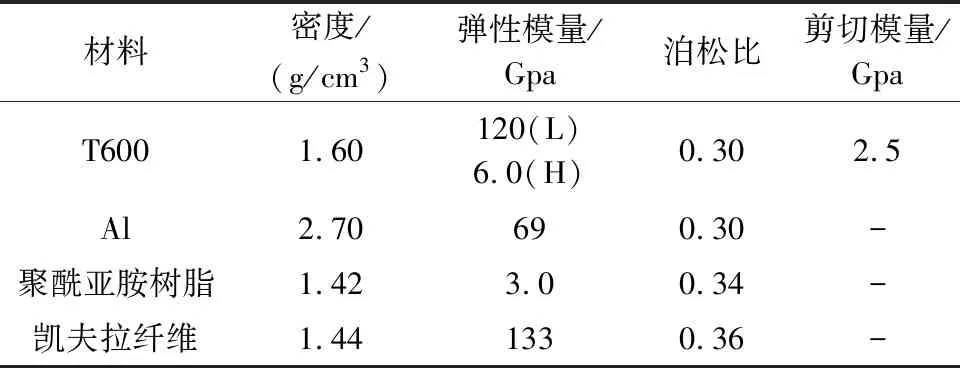
表1 材料性能参数(常温)Tab.1 Material performance parameters

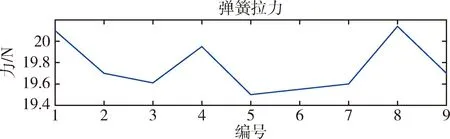
图6 稳态拉索拉力Fig.6 Steady cable force

图7 薄膜结构前6阶频率及振型(有限元)Fig.7 Membrane structure vibration modes(FEM)

3 参数辨识算法

本文基于CMIF[18]进行模态参数辨识.

步骤1.利用仿真实测数据绘制的频响函数矩阵H(jω)∈CNo×Ni(No、Ni分别表示输出、输入数目)在固有频率附近进行奇异值分解,有如下公式:

[H]=[U][Σ][V]H

(11)

式中:U为左奇异矩阵,对应于模态振型向量矩阵;Σ为对角线型奇异值矩阵;V为右奇异矩阵,对应于模态参与因子向量矩阵.

步骤2.构造增强频响函数,其表达式为

Hen(jω)=uHH(jω)v

(12)

式中,u∈CNo×1、v∈CNi×1分别是U、V的第一列向量.

步骤3.对式(12)得到的增强频响函数在每阶固有频率附近进行单自由度系统拟合

(13)

式中,λ为极点,未知数b1、b0和λ可通过最小二乘拟合计算得到

Xθ=Y

(14)

式中,X、Y和θ的表达式为

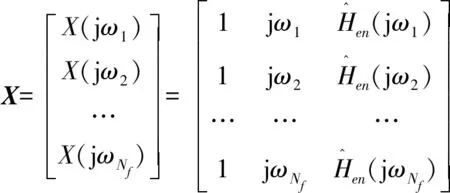
(15)

式中,Nf为给定频段内所包含的谱线数.

步骤4.计算出b1、b0和λ后,可计算固有频率f与阻尼比ξ

(16)

4 数值仿真及分析

本文基于多体系统动力学软件(MBDyn)[19]建立大挠性太阳翼多体模型,见图8.

图8 太阳翼仿真示意Fig.8 Solar wing simulation

利用第2.3节建立的薄膜结构平面太阳翼模型,综合考虑太阳光压力、气动阻力、重力梯度力矩和地磁力矩在内的复杂空间环境干扰,在可展结构连接点施加高斯白噪声加速度激励作为输入数据,通过瞬态非线性动力学分析,在薄膜阵面和边框上取图5所示共计54个点的位移响应作为输出数据.由于不同模态的贡献沿频率轴变化,因此在特定频率下,两种模态的贡献可以大致相等.在此频率下,这两条特征值曲线相互交叉.由于频率分辨率和CMIF绘制方式的限制,较低的特征值曲线出现峰值,而较高的特征值曲线出现下降,这样就会导致虚假模态的出现.本文采用模态相位共线性法(modal phase collinearity,MPC)根据辨识得到的各阶模态矢量实部和虚部之间的关系来判断模态的真假.MPC定义如下[20]:

(17)

(18)

式中,第j个模态的振型为φj,λ1、λ2分别表示Scov特征值的最大值和最小值.如果仅一个特征值与0不同,则在复平面中呈现完美的共线性,MPC会等于1,如果两个特征值相等,则不存在共线性,MPC会等于0.

瞬态动力学仿真过程中步长取0.001 s,仿真时间为100 s,延长原始数据至300 s并作加窗处理.如图9所示,在2 Hz内6个频率下,对应的奇异值存在极大值.如表2所示,由仿真数据辨识出的前3阶模态的MPC值接近1,可排除虚假模态.但是第4阶模态的MPC值显著降低,消除环境干扰后进行模态辨识,第4阶模态的MPC显著趋向于1,可见环境干扰会影响模态之间的相位关系,从而导致较低的共线性矩阵值.图10为辨识结果,可以看出辨识结果与有限元分析的振型吻合较好.

表2 模态MPC值对比Tab.2 Modal MPC values comparison

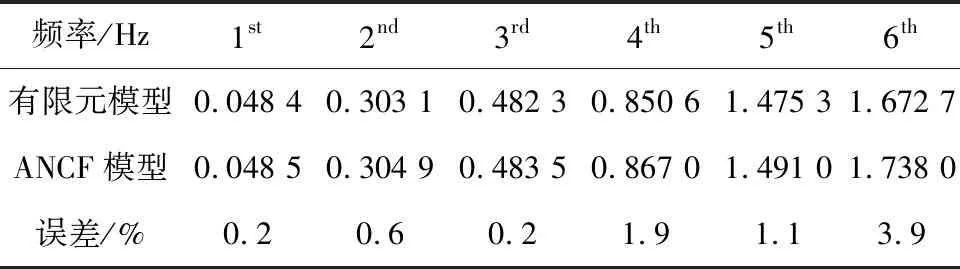
表3 固有频率辨识结果Tab.3 Natural frequency identification results

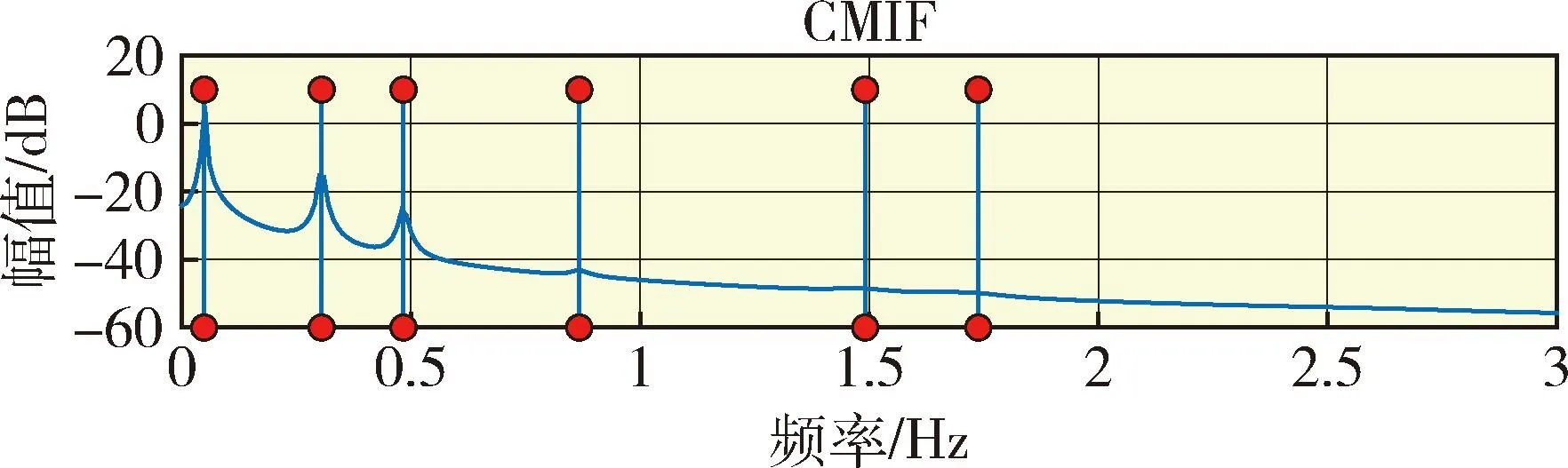
图9 CMIF峰Fig.9 CMIF peaks

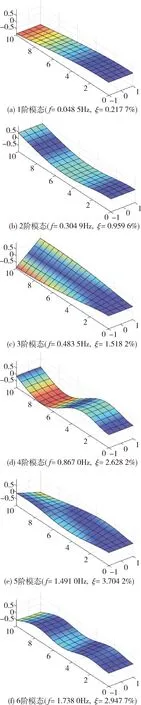
图10 模态辨识结果Fig.10 Modal identification results

5 结 论

结合可展薄膜结构平面太阳翼纤薄和轻柔的特性,本文建立了考虑拉索预应力的大型空间可展结构的动力学模型,利用CMIF对复杂空间环境干扰下的太阳翼模型进行模拟在轨模态辨识.仿真结果表明,CMIF方法可以有效辨识出薄膜平面结构的低阶模态,辨识结果与有限元分析的比对误差小于4%,可为后续开展工程化实施和在轨振动控制提供有效指导.

但是,在输出数据采集过程中没有考虑信号噪声和结构非线性等因素的影响,体现为频率辨识结果可能与实际传感器数据分析结果存在较大差距.因此,下一步的工作目标是探究CMIF识别算法中模态参数不确定性的计算方法.