航天器在轨角动量演化及卸载策略研究

谢 军, 刘新彦

北京控制工程研究所, 北京 100094

0 引 言

航天器在轨飞行,总要承受外扰力矩的影响,如果卫星有角动量交换装置,可以利用角动量装置的角动量吸收能力而保持姿态稳定,干扰角动量积累到一定程度,使用外力矩进行卸载,保障角动量装置能持续对卫星有效控制.对于不能提供角动量容量的欧拉轴,干扰力矩角动量的累积就直接表现为卫星的姿态运动,需要及时卸载[1-2].对于地球静止轨道卫星,由于磁场较弱,除对轨道预报精度要求较高的卫星外,一般使用推力器卸载角动量[3-7].在卫星的角动量测量上,角动量总是直观地体现在本体上的分量,但从卸载的意义上来说,需要尽量容忍角动量在惯性空间上的交变量,卸载掉惯性累积量,这样能够达到卸载次数少,节省推进剂;同时又有效地提高了推力器的工作寿命.本文研究了外扰力矩累计结果在整星上的表现,针对卫星的角动量累计特点,给出了卸载槛值和卸载量的定量公式.根据一些在轨卫星非正常卸载情况的分析结果,提出了解决措施,并在轨进行了实施,验证了论文观点的正确性.

1 卫星角动量的演化特点

地球静止轨道卫星主要的外干扰力矩是太阳光压干扰力矩.这类卫星通常具有较大面积的外伸固连天线、不对称帆板等,太阳光压干扰力矩的累积量是不容忽略的.对于具有较大惯性积的不对称质量特性卫星,其重力梯度干扰力矩造成的角动量累积也很可观.太阳光压干扰力矩和重力梯度干扰力矩经过多年的研究总结,文献中对其模型等已有较精确的描述[8-20].下面分别从俯仰通道、滚动偏航通道分析外扰角动量的累积,并以典型V型轮偏置动量卫星角动量累积过程与姿态的变化关系给出一个直观的说明.

1.1 外扰力矩在惯性系中俯仰方向累积特点

对于对地三轴稳定卫星,寿命期间在轨长期运动工况一般是卫星绕本体-y轴以轨道角速度大小在惯性系中转动,因此本体y轴角动量的积累方向是惯性方向,只要卸载掉卫星本体y轴上的角动量累积即可.但往往y轴方向不仅存在常值累计项,还存在日波动项,每天有一定的波动范围,不长期累积,因此卸载需要选择合适的门槛值,避免小于角动量日波动大小,造成喷气卸载的浪费和推力器无谓的工作.

y方向角动量的日波动项一般是在卫星本体xoz面内有一个伸出的一定面积的有效载荷如天线等受太阳光压干扰造成的.这种干扰的角动量积累在俯仰方向是一个周期变化过程,没有常值项.

y方向角动量的常值累积项一般由在xz方向有大的惯性积造成的.对于伸展开的大型展开天线,惯性积有的可以达到几万kg·m2,对于10 000 kg·m2的惯性积,y轴每天的角动量常值累积量可以达到近14 N·m·s,这是很大的扰动.

卫星俯仰方向的主要外扰力矩的角动量累积典型公式如式(1)所示

(1)

式中,a为每天的角动量常值累积项,b为每天的波动项,ω0为轨道角速度.

一般俯仰方向角动量的累积效果在卫星本体坐标系中观察(与惯性系一致)如图1所示.

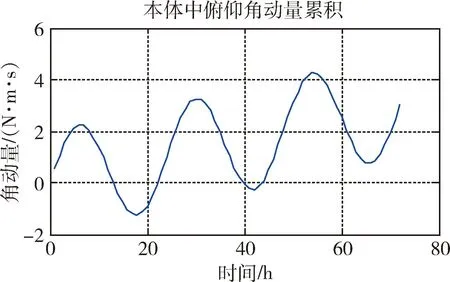
图1 俯仰方向角动量累计变化Fig.1 Cumulative change of pitch angular momentum

1.2 外扰力矩在滚动、偏航方向的累积及特点

外扰力矩对滚动、偏航通道的干扰角动量积累在惯性系中观察也存在常值项和交变项.常值项可以由单翼太阳帆板受晒引起,也可以由y方向伸展的有一定面积的载荷引起.日交变项主要是由于太阳矢量与轨道面有一定的夹角,太阳光压沿y轴有一定分量,对固连在卫星上在xoz面内有一定受晒面积的载荷引起的.

卫星本体滚动、偏航方向的角动量主要外扰力矩的角动量累积典型公式为

(2)

式中,a为惯性系中每天的角动量常值累积项,b为每天的波动项,ω0为轨道角速度,β为本体系相对轨道系干扰角动量波动项的相位角.

通过计算可以表明,惯性系下交变的角动量,在本体下也是交变的,但是在本体观察不会发散,而惯性系常值累积项,在本体系下观察,是逐渐交替发散的.对于惯性系下的累积项,在本体系下观察角动量变化如图2所示,其中的两天之间最大值的差值就是惯性常值累积量.

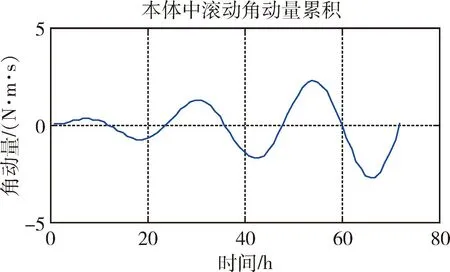
图2 滚动方向角动量累计变化Fig.2 Cumulative change of roll angular momentum

1.3 偏置动量卫星角动量演化和姿态的关系

一类典型的地球静止轨道通信卫星采用V型轮偏置动量构型.V型轮构型在-y方向有一定的角动量,俯仰方向的干扰角动量可以直接由轮系吸收;滚动方向的干扰角动量Hxd累积无法吸收,就表现为一定的偏航姿态,当Hxd累积到一定程度,达到偏航姿态的指标,需要卸载;偏航方向的干扰角动量Hzd影响的是滚动角,滚动角是实际可测量的,轮系可以提供偏航方向角动量容量,连续吸收干扰力矩,使滚动角始终被控制在指标范围内,但当轮系在偏航方向角动量增大到一定程度也必须卸载,避免V型动量轮角动量差异太大.

2 角动量的卸载策略研究

2.1 卫星俯仰方向角动量的卸载策略

基于式(1),在进行角动量卸载规律设计时,可以根据a、b的理论值考虑一定的余量设置卸载槛值Hgy,Hgy大小以不影响卫星的运行特性为准.

设角动量槛值为Hgy=na+b,不妨设a>0,超过Hgy就进行卸载.

则卸载量Huy的选择要满足式(3)约束.

(3)

这样的卸载策略保证一次卸载量适中,同时不会造成两边对喷.在轨运行时,可以根据实际的角动量演变曲线,统计求出系数a和b,调整卸载参数.俯仰方向角动量的卸载策略对偏置动量卫星和零动量卫星均适用.

2.2 零动量卫星滚动、偏航方向卸载策略研究

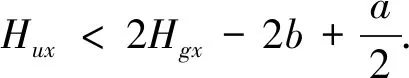
俯仰方向的卸载可以不用考虑相位关系,但滚动卸载则不同,上述卸载策略没有考虑相位关系和卸载量,相位并不是很重要,当角动量的波动量和常值项在几十个N·m·s时,就需要选择相位进行卸载,否则相位的弧段损失造成的推进剂浪费是很可观的,仍然要根据a和b设计卸载量,但要通过历史记录确定出角动量的最高点的相位,满足了卸载条件时,当卸载的方向和最高点相位一致,就可以最有效地卸载角动量累积项.偏航轴的卸载与此类同.

2.3 偏置动量卫星滚动、偏航角动量卸载策略

V型轮偏置动量卫星只能提供俯仰和偏航方向的角动量的容量,由于存在-y轴偏置角动量,在进行滚动或偏航方向角动量卸载时,需要把星体姿态运动和角动量运动结合起来,也就是进动和章动协调控制,达到姿态角度运动平稳,同时消除干扰角动量累积的目的.

图3是V型轮滚动角动量(对应偏航角)卸载过程机理几何表示.图中圆为卫星本体-y轴在惯性空间的运动迹,卫星由A点运行到B、C和D再回到A点为一个轨道周期,圆半径的大小代表了惯性空间角动量在xoz面内的分量大小,在物理概念上也反映了姿态角的大小,卫星从A点分别运行到B、C和D点,姿态从负滚动角分别转化为正偏航角、正滚动角和负偏航角,如果有外扰力矩,应是一个螺旋发散的过程.此处为了说明滚动角动量卸载过程,简化为圆表示.当卫星运行到B点时,偏航姿态角超出了指标范围,对应的是滚动角动量ΔHx超出了卸载槛值,卫星做如下卸载策略.

图3 V型轮偏置动量卫星滚动角动量卸载过程Fig.3 Unloading process of roll angular momentum of V-wheel bias momentum satellite

使星体在-z方向有BM大小的角动量变化,此时星体以M点为中心,BM为半径开始章动,-y轴端点运行OB/2大小后到达P点时,滚动施加大小为ΔHx=MN的角动量喷气量,星体以N点为中心,NP为半径开始章动,-y轴端点再运行OB/2大小后到达O点时,使星体在+z方向有NO大小角动量变化,使角动量端点与-y轴端点重合,这样使得章动和进动和谐统一,达到卸载的目的.

偏航角动量的卸载方式和滚动角动量卸载过程是一致的,在此不再叙述.

3 在轨卸载策略优化

3.1 零动量卫星俯仰角动量卸载策略优化及效果

某地球静止轨道零动量卫星的俯仰方向卸载策略为卸载槛值0.5 N·m·s,超过此槛值,就进行卸载,卸载量为0.5 N·m·s.设计时理论的俯仰方向角动量每天的波动量很小,基本上就是常值累计量,常值累计量每天也不超过0.5 N·m·s,这样设计卸载量可以满足理论的干扰力矩影响.实际在轨的俯仰方向角动量卸载情况如图4所示.

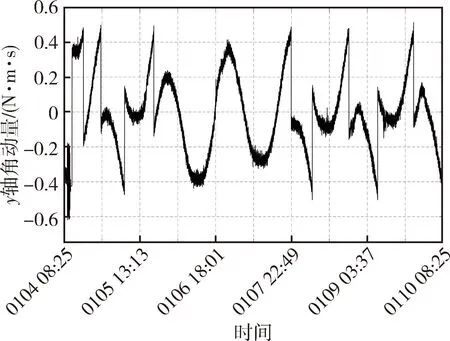
图4 某零动量卫星俯仰方向角动量曲线Fig.4 Pitch angular momentum curve of zero momentum satellite

按照式(1),从图4中可以看出,每天的干扰力矩常值累计量a=0.2 N·m·s,波动量为b=0.35 N·m·s,选择的卸载槛值和卸载量是0.5 N·m·s,Hgy=0.75a+b,卸载量也是Huy=0.75a+b.

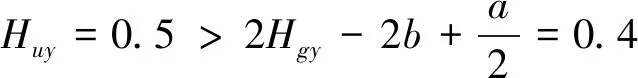
实际上,卸载一次后,星体俯仰角动量变为0,但角动量半天下行值一般应为2b-a,卸载后半天角动量为-0.6 N·m·s,显然超过了-0.5 N·m·s的卸载槛值,造成两端喷气.

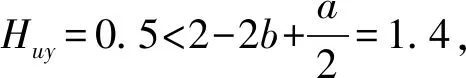
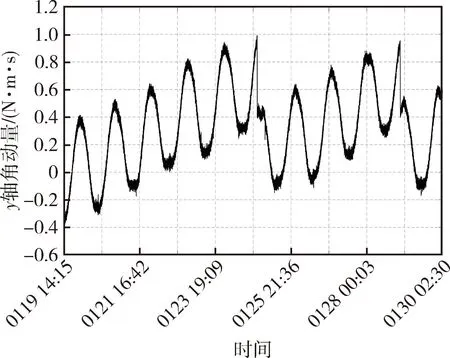
图5 某零动量卫星俯仰方向角动量卸载策略修正后的角动量曲线Fig.5 Pitch angular momentum curve of zero momentum satellite after modifying the unloading strategy

3.2 偏置动量卫星滚动、偏航角动量卸载频繁机理及解决

某地球静止轨道V型轮偏置动量卫星,滚动角动量卸载槛值设计为0.2 N·m·s,偏航角动量卸载槛值设计为0.3 N·m·s超过槛值,就进行卸载,消除干扰角动量累计值.

卫星在轨运行时,采用地球敏感器进行姿态测量,把滚动姿态测量和V型轮角动量偏差作为输入,利用角动量估计器实时估算滚动角动量Hxe和偏航角动量Hze.由于滚动角连续可测可控,Hze的物理意义为z轴方向V型动量轮角动量误差,Hze卸载使得两个动量轮偏差不至于过大,Hxe的物理意义为卫星偏航角的度量,选择合适的Hxe槛值卸载,使得偏航角控制在指标范围内.偏航估计器采用了两个动量轮在运行过程中的偏差作为观测输入,比较准确地估计出了y轴偏置角动量绕轨道法线偏差运动的情况,卸载量比较好地消除了这一偏差.实际在轨滚动、偏航角动量卸载情况如图6所示,一天卸载10次左右.

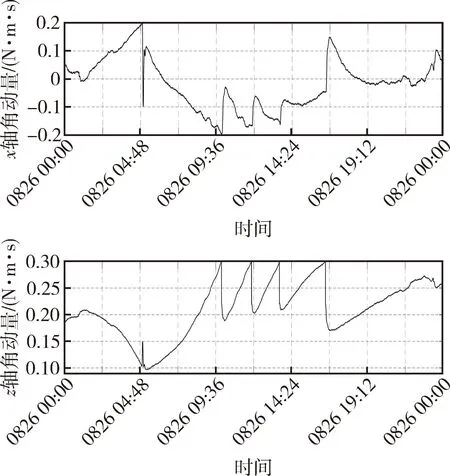
图6 滚动、偏航角动量曲线Fig.6 Angular momentum curve of roll and yaw

在卫星配置了星敏感器后,卫星三轴都有了测量,延续原有的利用Hxe和Hze进行卸载的控制策略,不再使用角动量估计器实时估算Hxe、Hze,而把星敏感器测量的滚动角、偏航角分别折算成Hxe、Hze.卫星在刚切换为星敏感器测量控制时,卸载次数明显增多,一天卸载约在20次左右,Hze卸载次数大为增加.卸载情况如图7所示.

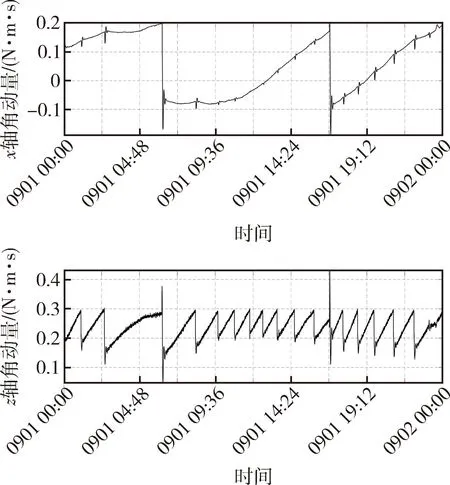
图7 姿态基准切换后的滚动、偏航角动量曲线Fig.7 Angular momentum curve of roll and yaw after attitude reference switching

利用无外扰力矩的情况下,角动量在惯性空间守恒的原理进行分析,定位为星敏感器测量偏航姿态存在误差造成多卸载.进行角动量演化和卸载分析,进入正常模式.如图8所示.

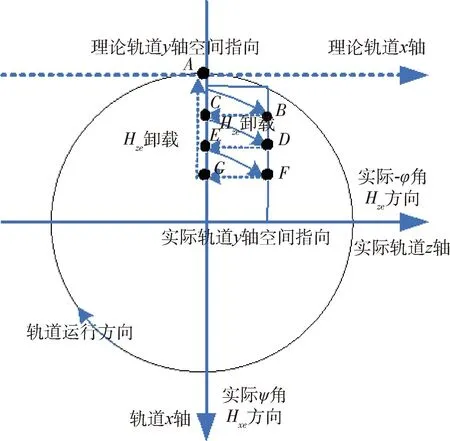
图8 偏航角动量频繁卸载示意图Fig.8 Schematic diagram of frequent unloading of yaw angular momentum

1)动量轮处于标称状态,滚动、偏航测量都是0姿态,处于A点,估计Hxe和Hze都是0,实际上卫星真正的偏航姿态是一定的负偏航姿态,在惯性空间存在角动量Hx,初值是Hx0,Hxe=Hx-Hx0(Hx0<0),Hze=Hz.

2)随着轨道运动,Hx向Hz转化,总是使Hz变化较快,Hx变化较慢,估计角动量Hze与Hz无偏差,使得Hze卸载,从A运行到B,卸载几次后,运行到G,卫星真正的惯性空间角动量Hx绝对值减小,但是由于有测量偏差,估算Hxe=Hx-Hx0,使得Hxe超差,进行Hxe卸载,从G到A.

3)运行周而复始,重复上述过程.实际上仅仅是由于偏航姿态测量误差引起角动量计算和实际角动量不一致,造成喷气过多,在一个轨道圈内多次Hze卸载,少量Hxe卸载,一圈的脉冲积分消除惯性空间角动量有限,大部分互相抵消,部分消除了空间外扰力矩的影响.

分析清楚喷气卸载频繁的机理后,进行数学仿真验证.偏航误差导致的滚动、偏航角动量仿真曲线如图9所示,仿真表明偏航角误差造成了Hze喷气卸载频繁.

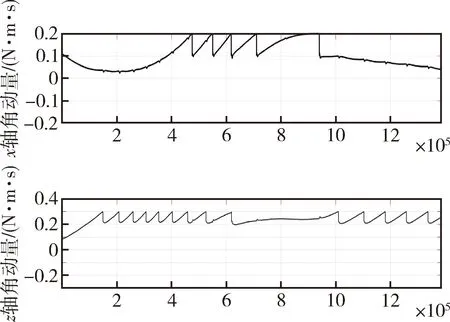
图9 偏航误差导致的滚动、偏航角动量曲线Fig.9 Angular momentum curve of roll and yaw caused by yaw error

基于分析与仿真的情况,进行星敏感器偏航测量误差补偿后,问题得到解决,补偿后的在轨卸载曲线如图10所示.后续在另一颗卫星上发生了Hxe卸载频繁的问题,分析表明是滚动角存在测量误差造成的,进行星敏感器滚动测量误差补偿后,问题也得到了解决,在此不再做过多分析.

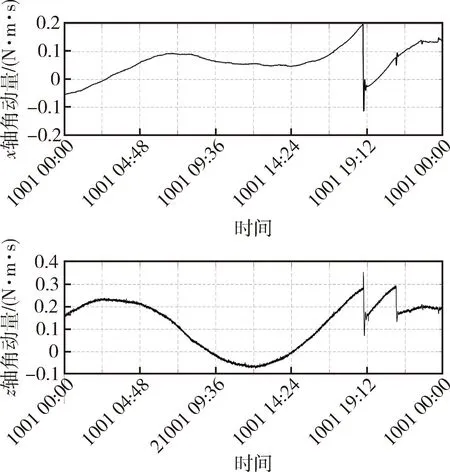
图10 偏差修正后的滚动、偏航角动量曲线Fig.10 Angular momentum curve of roll and yaw after yaw correction

4 结 论

本文阐述了地球静止轨道零动量卫星和V型轮偏置动量卫星的角动量累计演化特点,给出了量化的喷气卸载策略.以角动量演化的观点来解释卫星的姿态变化,物理概念清楚,问题描述简单并且有利于问题的解决.针对实际飞行的整星零动量卫星和V型轮偏置动量卫星在轨卸载所出现的问题进行了分析,提出了解决措施,经过了在轨飞行验证.