基于TEASER算法的空间非合作目标位姿估计

王世昌, 华宝成, 周依尔, 李小路*

1. 北京控制工程研究所 空间光电测量与感知实验室, 北京 100094

2. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191

0 引 言

在轨服务技术指一种为故障失效、燃料耗尽或者模块更换的卫星、空间站等目标提供维修服务的技术[1]. 根据是否事先安装可探测标记,空间目标可以分为合作目标与非合作目标[2]. 合作目标是指安装有激光角反射器或光学标记,或者能够主动与服务航天器通信的目标航天器. 而目前大多数在轨航天器都属于非合作目标,它们无法与服务航天器通信,且自身结构、尺寸和运动信息完全未知或部分未知[3]. 非合作目标的相对位姿测量是未来航天器持续发展、空间交会对接的前提与重点[4].

针对非合作目标的位姿测量主要采用可见光相机作为传感器,其测量结果直观,相关位姿解算方法成熟. 最常见的方法是提取图像中的特征点,再通过求解PnP问题即可得到目标位姿[5]. 但当空间光照或者目标位姿变化时,图像容易出现过曝、模糊和失真等问题,使得特征定位不准甚至无法提取,很大程度上影响了位姿求解精度. 随着主动式成像传感器(如激光雷达)的快速发展,基于点云的位姿测量技术逐渐发展起来. 与可见光相机相比,激光雷达可以直接获取目标的三维点云数据,包括空间坐标与纹理信息. 由于其主动式探测的特性使其不受光照影响,适合对目标的三维测量. 三维点云数据包含信息丰富,在空间非合作目标位姿估计方面具有独特的优势,是当前研究的热点[6-9].

目前,非合作目标三维点云位姿估计已应用于火星着陆、月球车避障和交会对接等领域[10]. 2006年,TERUI等[11]采用双目相机对左右图像进行立体匹配从而获取目标三维点云,并采用ICP算法将其与模型点云配准来估计目标位姿,三轴平移误差小于1cm,旋转误差小于5°.2012年,RUEL等[12-13]开发的 TRIDAR系统包含了激光雷达与相机,并采用ICP算法将点云与航天器模型配准,完成相对位姿测量,用于非合作目标自主交会对接与相对导航.2016年,LIU等[14]使用Flash激光雷达获取目标点云,进而采用ICP算法来完成位姿追踪,在仿真实验中平移误差小于4 cm,旋转误差约为1°.2019年,LI等[15]提出了一种基于连续点云的状态估计方法,利用扩展卡尔曼滤波估计目标的位姿参数. 最后,进行了半物理实验研究,位置误差小于5 cm,姿态角误差小于3°.2020年,LI等[16]通过提取飞行时间(time of flight, TOF)相机获取的卫星太阳翼平面点云进行粗配准,再进行ICP精配准,实现非合作卫星的位姿跟踪,旋转误差小于0.1°,平移误差小于2. 5 mm.

上述位姿估计方法大多以ICP算法为核心,但ICP的缺点是对初始值敏感. 同时,由于距离变化会使得目标点云空间离散程度不同,背景噪声的存在也会导致点云存在误差,不同传感器所获点云质量也有所不同. 上述问题都会影响最终的位姿估计结果,且不同实验条件与算法下所得指标也无法评估. 针对点间距及噪声变化对点云配准算法的影响,提出一种基于TEASER的位姿估计方法. 所提方法使用TEASER算法实现粗配准,可以降低误匹配对初始位姿的影响,然后采用ICP对位姿进一步优化,实现非合作目标高精度位姿估计. TEASER算法是YANG等[17]于2021年提出的一种全局配准算法,其可以鲁棒地求解含有大量外点的配准问题,使得位姿估计结果对误匹配不敏感. 本文首先将TEASER算法与随机采样一致性(random sample consensus,RANSAC)算法作对比,讨论点云噪声对算法的影响,并将TEASER与ICP相结合,实现了连续帧位姿估计.

1 方 法

基于点云的位姿测量的关键是在已知目标三维点云的基础上计算目标姿态,其核心问题是点云配准. 点云配准是求取两组点集之间的旋转与平移矩阵的过程,从配准过程而言,点云配准分为粗配准与精配准两个过程. 粗配准是指在两点云相对位姿完全未知的情况下对点云进行配准,主要用于两片点云相距较远、重合度较低的情形,可以获得一个粗略的配准结果作为精配准的初始值. 精配准的目的是在粗配准的基础上让点云间的空间位置差别最小化,ICP及其变种是使用最为广泛的算法. 基于点云的空间非合作目标位姿估计流程如图1所示.

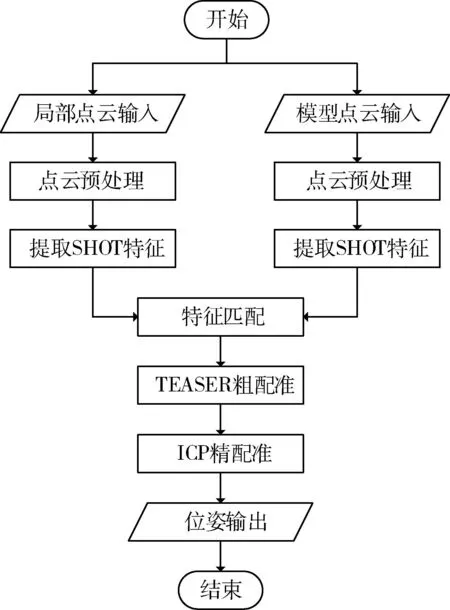
图1 空间非合作目标位姿估计流程图Fig.1 Flow chart of pose estimation for space non-cooperative target

首先是局部点云与模型点云读取,对点云进行预处理,主要是为了降低计算量. 然后对预处理后点云的每一点计算SHOT,方便后续特征匹配,其过程是对于局部点云中的每一个点根据特征描述子的相似程度,找到其在模型点云中的对应点,形成匹配对.根据已有匹配对进行粗配准,得到初始变换矩阵,再将结果传递给精配准部分,最终得到局部点云与模型点云的位姿变换关系.

1.1 SHOT特征提取

点云特征类似于图像特征,是对点云中某一点的邻域几何信息的描述或整体点云信息的描述,可以分为局部特征描述子与全局特征描述子[18].SHOT作为局部特征描述子的一种,具有旋转及尺度不变性,容错性较大,对于含有噪声的点云数据有较强的鲁棒性,常用于物体的位姿估计[19]. 基本思想是:对于点云中的每个查询点,先构建点邻域的协方差矩阵,再对协方差矩阵进行奇异值分解建立局部坐标系;以查询点为球心,将球形邻域按经线、纬线及径向方向共划分为32个子空间;计算每个子空间中的邻域点法线与查询点法线的夹角余弦值,再将每个子空间中的余弦值等分为11等份并进行直方图编码;最后将所有子空间的直方图组合在一起,形成352维的特征描述子.

1.2 TEASER算法

现有的粗配准方法主要分为两类:基于分支定界或点对点对应关系[20]. 基于点对点对应关系的配准方法具有更高效、稳定性更强等优点,是目前点云配准的一个标准方案. 该类算法大多是依赖基于点云局部特征描述与匹配建立的匹配对,也有一部分是基于二元或三元点对点对应关系. 而由于观测噪声的存在与点云结构的相似性,实际匹配中会有较多的误匹配,如何减小误匹配的影响成为粗配准中极其关键的一步.

六自由度的3D点云配准问题本质上是典型的非凸优化问题,其目标函数在六维可行域空间中具有多个波峰波谷,即优化求解过程中受初始变换矩阵影响,容易陷入局部最优解. TEASER算法将配准问题重新建模,采用半定松弛的方法求解了非线性、非凸优化问题. 假设两组点云ai、bi之间存在尺度、平移和旋转变换,则配准问题可以描述为

(1)

式中,s为尺度变换因子,R为旋转变换,t为平移变换,σi为噪声标准差. 实际匹配点对由于噪声的存在会有许多外点,为了让求解过程对误匹配点对不敏感,采用截断最小二乘(truncated least squares, TLS)为代价函数并改写式为

(2)

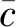
如图2所示,通过给具有较大残差的测量值分配常数代价,最小化问题时的最优解不会出现在水平阶段,从而使整个问题对外点不敏感.

图2 截断最小二乘估计Fig.2 Truncated least squares estimation

但是,这个问题仍是非线性最小二乘问题且非凸,穷举搜索全局最优解的时间复杂度为O(2N).为了能在多项式时间内求解该问题,TEASER根据2个事实将式(2)分解为尺度、平移和旋转变换3个独立问题,并分别求解.

第一个事实是平移不变测量,即点云在平移过程中,其中任意两点组成的向量的方向不变,如图3所示.

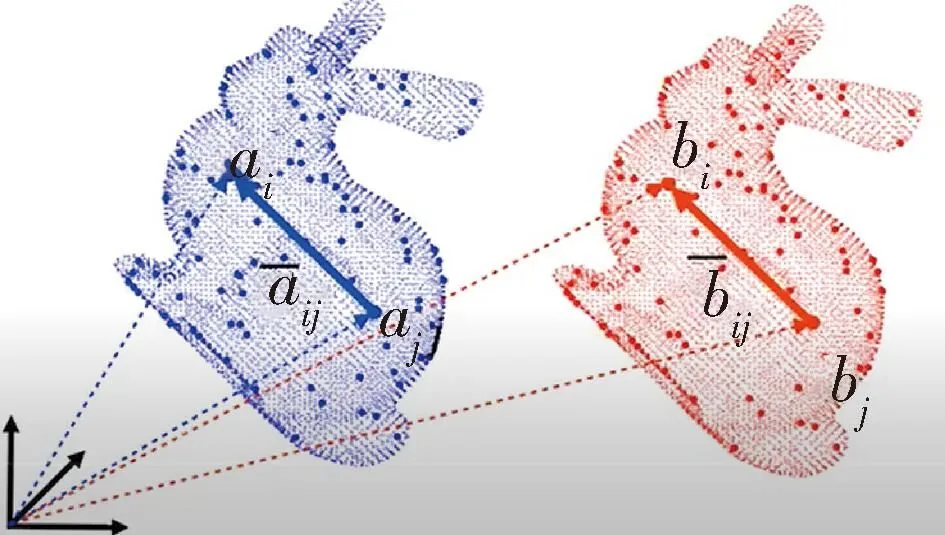
图3 平移不变测量Fig.3 Translation invariant measurement

假设两片待配准点云ai、bi符合以下模型:

bi=sRai+t+oi+εi

(3)

式中,εi为测量噪声,假设噪声服从高斯分布且有界.如果(ai,bi)构成内点,则oi为零向量,否则为任意值. 根据以上模型,令bj减去bi得

(4)

第二个事实是平移旋转不变测量,即点云在平移与旋转过程中,其中任意两点组成的向量的模值不变,如图4所示.

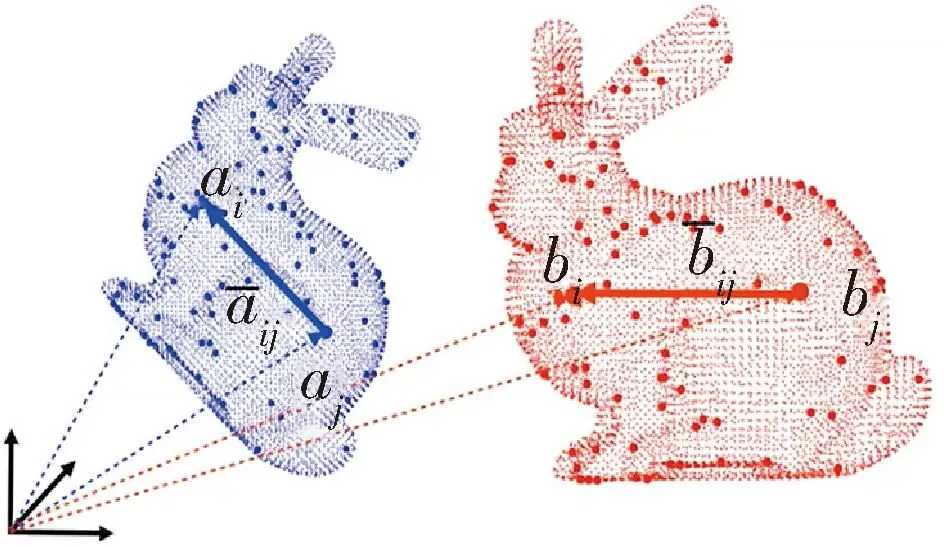
图4 平移旋转不变测量Fig.4 Translation and rotation invariant measurement

对式(4)取模可得

(5)

(6)

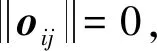
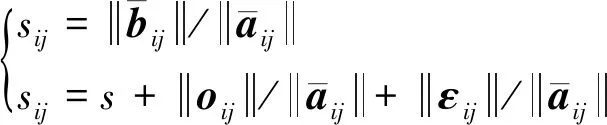
(7)

可知:利用平移旋转不变测量后,式(3)只与尺度变换因子有关. TEASER算法需要先利用平移旋转不变测量求出尺度变换估计值,然后根据平移不变测量与尺度变换估计值求得旋转变换估计值,最后将尺度变换估计值与旋转变换估计值代入式(2)即可求出平移变换估计值,从而完成基于截断最小二乘的点云配准问题的求解.

1.3 ICP算法

ICP算法是点云配准中最为经典的精配准方法,自提出以来就受到人们的广泛关注,后续的诸多精配准算法也是基于ICP进行改进[21]. 其基本思想是:分别在源点云与目标点云中,按照约束条件找出最近对应点,然后迭代计算变换矩阵直到误差函数最小.

2 实验验证

对服务航天器来说,当其执行对接、捕获等任务时,必然会逐渐靠近或远离目标航天器. 由于传感器分辨率有限,不同距离下所获点云疏密程度不同,传感器的观测噪声则会引入离群点与噪声点,这些都会使特征提取和匹配环节出现错误. 如何保证配准算法对于点云分辨率变化与点云噪声变化的鲁棒性,是点云粗配准的关键. 为了验证TEASER算法的鲁棒性,本文将其与RANSAC算法作对比,开展不同噪声水平与不同分辨率场景下的点云粗配准实验,并结合ICP精配准实现精确位姿估计.

2.1 实验描述

实验中所用目标为北斗卫星,其长、宽和高分别为17.15 m、2.81 m和5.5 m.定义目标坐标系为:水平向右为X轴正方向,竖直向上为Y轴正方向,再根据右手准则即可确定Z轴正方向. 为了模拟不同距离、不同姿态下的目标点云,实验中通过在Blensor仿真软件中导入已有的模型文件,并预设目标距离虚拟相机5～15 m、姿态角为-90°～90°,共获得15组不同位姿下的场景点云.

点云分辨率指的是点云中两点之间的平均距离,反应了点云的密集程度,计算公式如下:

(8)

式中,n表示点云中点的数量,di表示点云中第i个点与其最近邻点的距离.

为了获得不同分辨率的点云,本文对原始模型点云进行了均匀降采样,并经过随机变换得到15组不同位姿的场景点云,每个场景均获得8种不同分辨率的点云. 类似地,为了模拟传感器获得的实际场景点云中的噪声,本文在场景点云中添加均值为0、标准差为σ=c×pr的高斯噪声,测试点云噪声变化对配准结果的影响. 其中c是调节因子.

为评估变换的估计值与真实值之间的差异,本文采用旋转误差与平移误差两个常用的点云配准评价指标. 对于给定的目标点云Ptgt,源点云Psrc与Ptgt之间的变换关系T可以由点云配准计算求得,Psrc与Ptgt之间的残差变换ΔT定义为

(9)

式中,T为源点云Psrc到目标点云Ptgt变换的估计,Ttruth为二者之间的真实变换关系. 进而可求得Psrc到Ptgt的旋转误差erot、平移误差etra为

(10)

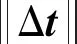
2.2 实验结果与分析

2.2.1 点云粗配准算法评估

(1)点云分辨率变化分析

为了比较RANSAC和TEASER两种粗配准算法对点云分辨率变化的鲁棒性,本文开展了不同降采样场景下的粗配准误差对比实验. 将降采样后的场景点云与已有的模型点云进行配准,统计不同降采样率场景的配准误差,如图5所示.

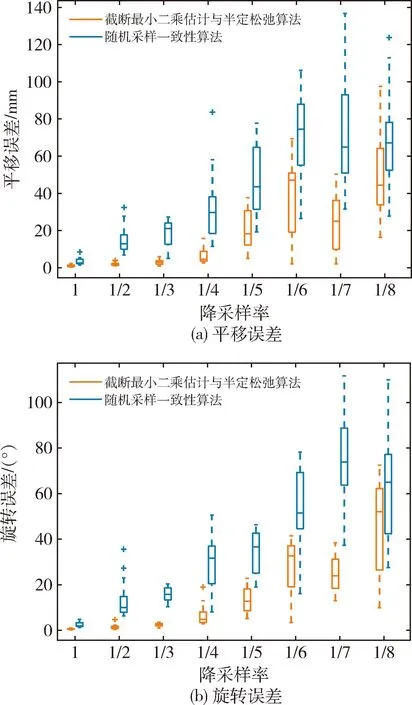
图5 点云分辨率对粗配准的影响Fig.5 Effect of point cloud resolution on coarse registration

随着降采样网格半径的增加,两种算法的配准误差均逐渐变大. 半径越大,原始场景降采样后的点云点数越少、点云分辨率越大,容易发生误匹配. 同一降采样网格半径下,TEASER配准误差的变化小于RANSAC. 当降采样率不超过1/5时,TEASER配准误差波动范围更小,TEASER算法求得平移误差最大为3.77 cm,旋转误差最大为22.1°,而RNASAC算法求得的平移误差最大为8.36 cm,旋转误差最大为50.5°.

(2)点云噪声变化分析

为了对比两种算法对点云噪声变化的鲁棒性,本文通过在场景点云中添加均值为0、标准差为σ=c×pr的高斯噪声,测试点云噪声变化对配准结果的影响.统计不同噪声场景下两种算法的配准误差,如图6所示.

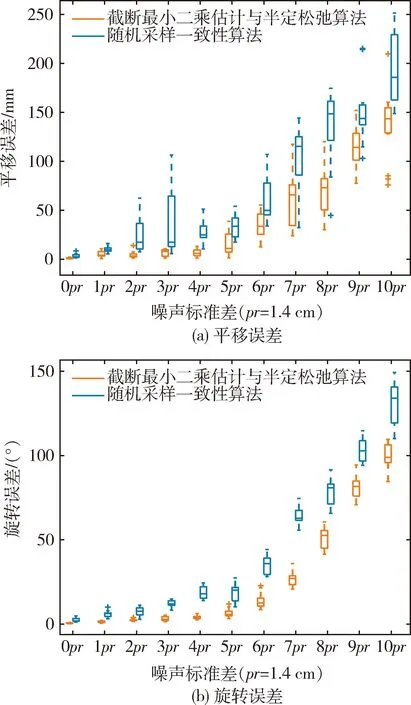
图6 点云噪声对粗配准影响Fig.6 Effect of point cloud noise on coarse registration

对于单一算法来说,旋转误差与平移误差均随着噪声标准差的增加而增加. 对比不同算法在同一场景下的误差,可以看出:噪声一定时,采用TEASER算法求得的配准误差总是小于RANSAC算法所求结果. 无噪声时,TEASER的平移误差最大为2.3 mm,旋转误差最大为0. 97°;当σ≤5pr时,TEASER的平移误差最大为3. 88 cm,旋转误差最大为12. 1°. 噪声标准差的增加对于TEASER算法影响较小,而RANSAC性能退化较快,这说明了TEASER比RANSAC的抗噪声性能更好.

从以上实验可以总结出:无论是点云分辨率还是点云噪声变化,TEASER算法的配准结果要优于RANSAC,且在低噪声场景下的误差稳定性更好. 这是因为RANSAC基于穷举搜索的思想,其假设每次选择的随机匹配对均是正确的,而在实际场景中,由于目标局部结构的相似性或者噪声点的干扰会产生误匹配,从而对求解结果造成较大影响.TEASER从配准问题的鲁棒求解出发,针对配准中存在的大量外点,采用截断最小二乘函数为代价函数,在一定程度上避免错误匹配对配准结果的影响.因此在面对由于环境噪声或者点云稀疏形成的误匹配时,TAESER算法比RANSAC算法更加鲁棒.

RANSAC与TEASER两种方法在无噪声场景下配准结果如表1所示,可见,TEASER的配准精度优于RANSAC,运行效率也较高.

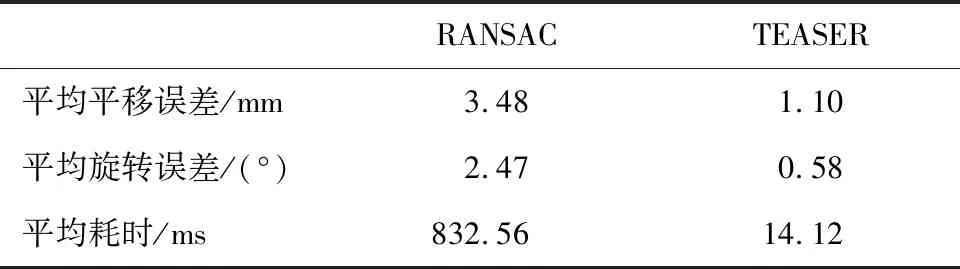
表1 无噪声情况下RANSAC与TEASER的性能对比Tab.1 Comparison of RANSAC and TEASER without noise influencing

2.2.2 结合ICP精配准算法评估

为了进一步优化位姿估计结果,本文将TEASER粗配准结果输入给ICP,最终得到目标精确位姿估计值,部分配准结果如图7所示.

图7 精配准(绿色为模型点云,蓝色为仿真点云,红色为配准结果)Fig.7 Fine registration (the green one is model point cloud, the blue one is simulation point cloud, and the red one is registration result)

统计不同噪声标准差下的目标位姿估计误差如图8所示.从图中分析可得:经过ICP算法优化后,位姿估计的平移与旋转误差均有所下降. 在无噪声情况下,加入ICP精配准后的平移误差小于1 mm,旋转误差小于0.5°;随着高斯噪声的加入,同一帧点云中点的位置产生变化,实际匹配对与真实对应关系相比会存在偏差,使得最终位姿估计误差逐渐增大. 当添加的噪声标准不超过5pr时,平移误差最大为1.66 cm,旋转误差最大为2.67°,仍具有较高的精度;当噪声继续增加到10pr时,此时场景点云结构信息缺失,TEASER粗配准后无法提供精准初始位姿,ICP失去优化作用.

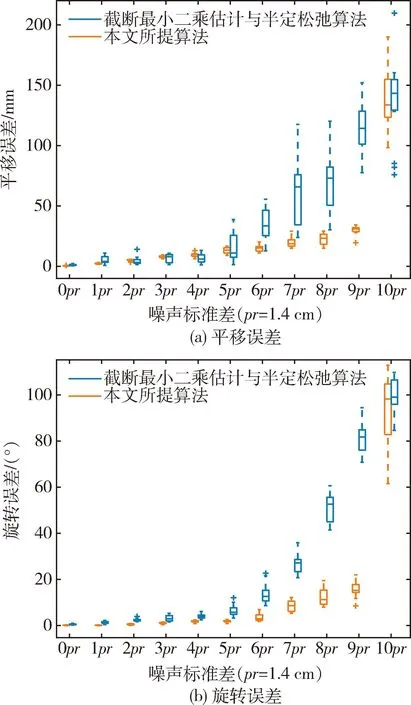
图8 目标位姿估计误差Fig.8 Target pose estimation errors

2.3 连续帧位姿估计

在服务航天器与目标航天器的相对运动过程中,需要不断获取目标位姿信息来引导自身运动. 由于相邻时刻间运动幅度较小,目标局部点云重叠度高,因此可以直接利用ICP方法估计相邻帧之间的运动. 为了实现目标的连续帧位姿估计,可以将整个过程分为两部分:初始位姿估计与连续位姿估计. 以某时刻目标航天器所在位置为基准,通过将第一帧点云与已有模型点云配准即可计算出目标在服务航天器坐标系下的初始位姿,也即初始化过程. 之后,通过关联相邻时刻的点云数据进行位姿变换矩阵参数的传递,来完成航天器的运动跟踪,最终解算出当前时刻目标航天器相对于服务航天器的绝对位姿,实现连续帧位姿估计.

随着时间的增加,由于帧间配准误差的不确定性,传统ICP方法会存在累计误差. 本文采用了周期关键帧配准方法,降低配准误差随时间增加而发生的漂移,其中本文中算法的关键帧为初始第一帧点云,如图9所示. 所提算法为每隔一定周期将当前帧点云与第一帧点云配准,实现当前周期初始点云的位姿估计. 周期内的点云位姿仍基于临帧ICP估计结果.

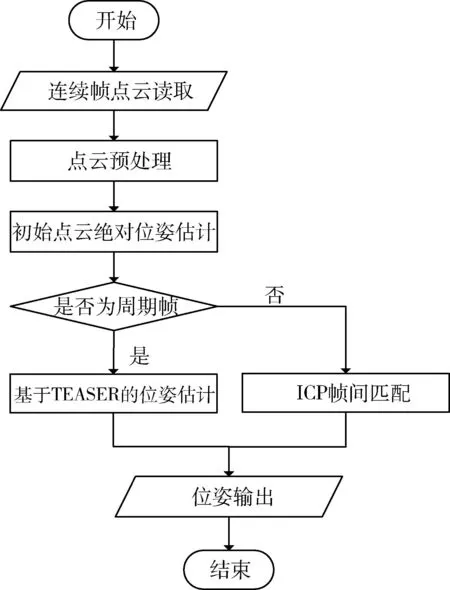
图9 周期关键帧配准流程图Fig.9 Flow chart of periodic keyframe registration

为了验证上述方法的有效性,本文通过仿真软件模拟目标运动过程中的连续帧点云,每隔10帧点云进行一次关键帧配准,实现了目标在平移与旋转运动下的连续帧位姿估计.

(1)旋转运动

旋转是空间目标最常见的运动形式之一,实验中规定目标做单轴旋转运动. 假设目标绕其Z轴以5(°)/s的速率匀速旋转,旋转角从-50°～50°,虚拟相机帧率为10 Hz,则共得到201帧连续点云,部分帧点云数据如图10所示.

图10 部分帧点云Fig.10 Partial frame point cloud

根据仿真点云,分别采用传统ICP帧间匹配与周期关键帧配准方法,解算得到每一帧点云的绝对位姿,统计估计误差结果如图11所示. 从两幅图中可以发现:随着时间的增加,传统ICP方法的估计误差逐渐变大;而本文所提方法的平移误差曲线维持在较低水平,有周期性变化趋势. 在无噪声情况下,所提方法平移误差最大为1.39 cm,旋转误差最大为0.5°,平均平移误差降低了85.7%,平均旋转误差降低了68.8%.

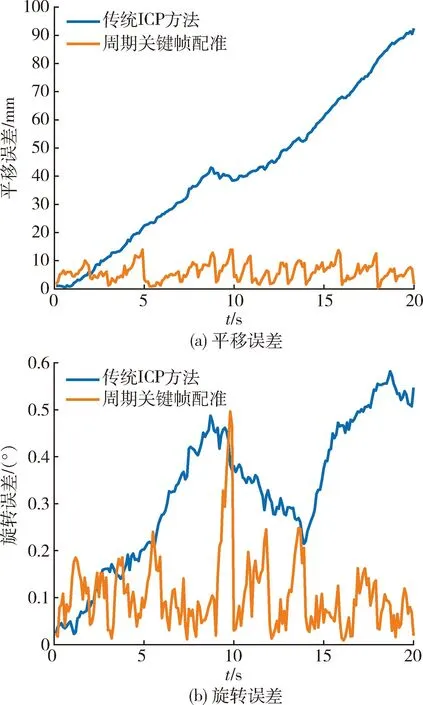
图11 旋转运动下连续帧位姿估计Fig.11 Pose estimation of continuous frames of rotation

(2)平移运动

为模拟服务航天器与目标航天器的相对平移运动过程,令目标沿其Z轴做匀速直线运动,速度为0.5 m/s,目标与相机的相对距离从20 m变至10 m,共得到201帧连续点云.同样地,统计两种方法计算所得每一帧目标航天器的绝对位姿估计误差如图12所示.

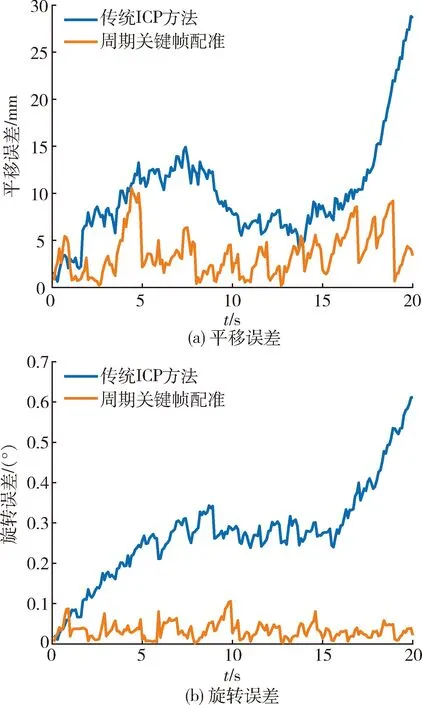
图12 平移运动下连续帧位姿估计Fig.12 Pose estimation for continuous frames of translation

从图中可知:传统ICP方法所得的平移与旋转误差曲线均会随时间发生漂移.在无噪声情况下,本文所提方法的平移误差最大为1.05 cm,旋转误差最大为0.1°,平均平移误差降低了65%,平均旋转误差降低了89.3%.

(3)复合运动

一般情况下,平移与旋转运动是耦合且相互影响的.为了验证周期关键帧配准方法的有效性,本文开展了目标同时做平移与旋转运动时的连续帧位姿估计实验分析.

假设目标沿着其Z轴以0.5 m/s的速度做匀速直线运动,距相机从20 m运动至10 m,同时绕着其Y轴以5(°)/s的速率旋转,旋转角从-50°～50°,共获取201帧点云.考虑到由于环境及传感器引起的点云噪声问题,实验中为连续帧点云添加均值为0,标准差σ=3pr的高斯噪声,对比传统ICP方法与所提周期关键帧配准方法的位姿估计误差结果如图13所示.

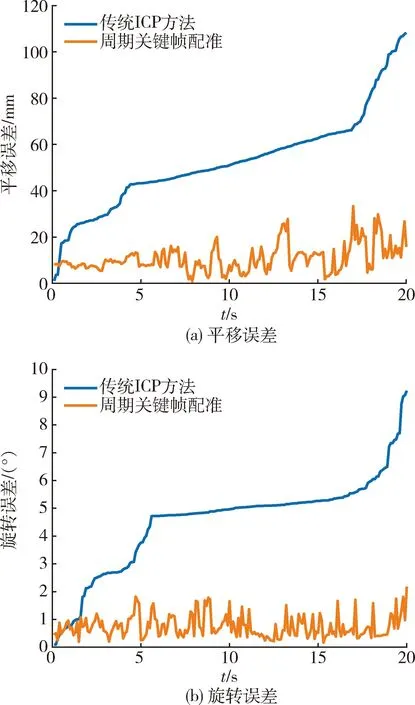
图13 复合运动下连续帧位姿估计Fig.13 Pose estimation for continuous frames of compound motion

从图中可以发现,随着时间的推移,基于ICP所得的连续帧绝对位姿误差逐渐变大,其中平移误差最大达10.82 cm,旋转误差最大达9.23°.而周期关键帧配准方法所得的误差曲线并未呈发散趋势,有效减小了累计误差,平移误差最大为3.33 cm,旋转误差最大为2.18°.与传统ICP方法相比,所提方法的平均平移误差降低了79.6%,平均旋转误差降低了83.4%.平移与旋转误差变大是因为噪声的加入导致了点的坐标发生偏差,导致根据特征匹配找到的对应点与真实对应点相比存在误差,从而造成最终的求解误差增大.实验表明:当目标做复合运动且点云含有噪声时,周期关键帧配准方法的平移与旋转误差变大,但仍可以有效降低传统ICP方法的累计误差.

实验中同时发现,平移与复合运动连续帧位姿估计中,从第17 s开始误差曲线有发散的迹象.为了分析这一现象的原因,利用局部点云表面积与模型点云表面积之比定义了点云局部率,并分析了连续帧点云局部率变化情况.平移运动实验中,点云局部率从最大0.32逐步下降至0.005;而旋转运动实验中,点云局部率始终在0.3左右.这是因为旋转时目标与相机间距不变,并始终保持在相机视场中;而目标发生平移时,目标与相机间距逐渐减小,目标只有部分出现在相机视场中.平移运动实验中,当时间大于17 s时,目标点云局部率小于0.03,说明此时目标点云所含信息较少,部分结构信息缺失.在利用基于TEASER算法进行周期帧的位姿估计时,SHOT描述子计算不准确使得误匹配增加,因此周期帧的位姿估计结果产生误差,后续的ICP帧间匹配无法修正该误差,故误差曲线呈发散趋势.

3 结 论

针对基于点云的空间非合作目标位姿估计问题,本文利用TEASER与ICP结合算法,实现目标位姿求解.同时提出一种周期关键帧配准方法,解决配准误差随时间发生漂移问题.实验结果表明,与传统RNASAC算法相比,采用TEASER与ICP相结合的算法实现位姿估计具有更高的精度.在连续帧位姿估计中,提出一种周期关键帧配准方法.与传统ICP方法相比,所提方法的平均平移误差与旋转误差均降低.其中,平移误差小于3.33cm,旋转误差小于2.18°.上述方法可以为空间非合目标位姿估计提供算法理论基础.

实际情况中,由于目标点云噪点过多使得目标几何结构信息丢失导致误匹配占比高,本文方法在严重噪声干扰条件下仍具有提升空间.此外,本文采用传统的最近邻搜索寻找匹配对,效率较低.为进一步提高位姿估计的效率以及鲁棒性,下一步工作将优化特征匹配环节,减少耗时,提高匹配对的准确性.