一种基于STL-Prophet-Informer模型的太阳电池阵多变量趋势预测方法

张舒晗, 程月华, 姜 斌

南京航空航天大学自动化学院,南京 211100

0 引 言

随着空间技术的不断发展,卫星目前在军事、民用、资源勘查等领域有着不可替代的作用.然而,卫星所处的太空环境极为恶劣,太空垃圾、粒子辐射等会不断影响部件磨损老化,并且由于卫星自身的构造也愈发复杂,因此卫星在轨运行期间有很大概率会出现各种异常或故障[1].根据数据统计,在卫星故障占比最大的电源分系统中,大约42%的故障源于太阳电池阵,因此太阳电池阵是研究人员主要关注的对象之一.遥测数据是反映卫星运行状态和部件性能的重要参数之一.针对太阳电池阵遥测数据开展趋势预测研究,能为卫星的动态健康监测提供有力的帮助,从而提高卫星的自主运行性能,一定程度上延长卫星的使用寿命[2].

传统的趋势预测方法主要包括基于模型的趋势预测技术、基于概率统计的趋势预测技术和基于数据驱动的趋势预测技术.基于模型的趋势预测,其必要条件是可以通过对系统机理的分析得到系统精确的数学或物理模型.通常应用于所研究的对象系统精确的物理或者数学模型的建立较为简单的情况.通过分析系统的概率统计特性,得到研究对象的趋势预测信息的技术,就称为基于概率统计的趋势预测技术,常用的方法包括时间序列预测法、模糊逻辑法和回归预测法等.对于平稳时间序列的预测问题,文献[3]将随机性这一概念加入到时间序列模型中,并成功提出自回归(autoregressive, AR)模型.在AR模型之后,研究人员又提出了著名的滑动平均(moving average, MA)模型,文献[4]提出的沃尔德分解定理成为了后续研究时间序列预测问题的基础.直到上世纪70年代,自提出回归滑动平均(autoregressive moving average, ARMA)模型[5],平稳时间序列建模问题开始有了成熟的解决方案,它成为时间序列分析方法最基本的工具,也是应用最为经典且成熟的模型之一.例如文献[6]研究了基于自回归模型(AR)的航天器故障状态预测方法,证明在航天故障领域,应用时序数据模型是可行的.文献[7]针对原始数据中存在的周期性、季节性和假日性等因素,选用了一种基于Prophet的电力系统预测模型,并在真实数据集上得到了优秀的效果.对于难以建模的系统对象,可以考虑使用系统自身的传感器的数据或者遥测到的时间序列数据,寻找数据中的内在信息,即基于数据驱动的趋势预测技术.典型的基于数据驱动的预测方法所使用的核心技术是人工智能技术.近年来,深度学习大行其道,神经网络在诸多领域取得成功,其成果开始向其他领域扩展.文献[8]提出了一套以模糊c-means聚类和SVM为核心框架的建模方法,通过对不同的时间序列数据集的研究,结果表明该模型在预测精度上胜过了其他方法.在文献[9]中,研究者采用LSTM模型来预测带有长期和短期相关性的石灰序列.实验证明,LSTM模型的预测结果较传统的自回归模型更为优越.文献[10]利用双向长短期记忆网络进行卫星任务的在线预测,取得了良好效果.文献[11]将Seq2seq和Attention引入模型,利用卷积神经网络对台风图像进行台风等级预测,在不同分辨率图像下提高了准确度.文献[12]将TCN于LSTM网络结合,对电力系统负荷进行短期预测,相较于传统算法预测误差均有减小.文献[13]利用改进的Faster R-CNN模型应用于卫星部件的失效检测,在小部件检测的准确率与召回率上有所提高.目前,Transformer无疑是深度学习领域最火热的模型之一,最早用于机器翻译任务,由于其在文本、语音和图像等领域均取得了现象级的效果,因此也被逐渐应用到时间序列预测领域.它使用了自注意力机制对序列信息整体处理,能够避免信息的递归传递,同时能重点关注具有强相关性的局部信息.文献[14]提出了一种新方法,使用基于Transformer的预测模型来预测未来数据,并利用模型的自注意力机制从输入数据中学习数据的变化模式.

总的来说,目前广泛应用于太阳电池阵等卫星电源系统零部件参数趋势预测的方法大多基于循环结构网络,如RNN和LSTM.该类模型虽然相比其他确定性和传统统计学模型能够更好地解决序列预测问题,但由于其对时序信息进行顺序提取并不断向后传递,在从预测单变量到预测多变量时,则会包括更多历史信息而导致输入序列较长,就容易出现梯度消失和梯度爆炸问题[15],致使模型难以训练或无法训练,这将导致模型在处理线性的预测问题时,预测的效果将不如普通的时间序列模型[16],极易出现过拟合.与此同时,虽然神经网络模型从精度上可以很好地解决非线性的预测问题,但是由于缺乏可解释性,无法量化地描述待分析参量与其他参量之间的关系和其他参量对于预测参量的贡献值.

针对长序列的遥测数据预测问题,本文将采用Informer[14]模型解决.它是基于Transformer模型针对时间序列预测问题的有效改进.它使用了自注意力机制对序列信息整体处理,能够避免信息的递归传递,同时能重点关注具有强相关性的局部信息.Informer专门设计用于解决长时序预测问题,对Transformer 原有的自注意力机制进行了概率稀疏化,减少了计算复杂度以达到更轻量级的模型部署,并有效提高了序列预测的准确度.由于稀疏自注意力机制,相比于LSTM模型,在长序列的建模下有着更高的精确性和可扩展性.

为了进一步提高预测精度,考虑到以上Informer模型对于多变量时间序列建模的优势,本文选择将经过STL分解后得到的周期性和残差分量(非线性)采用Informer模型进行预测.对于经过STL分解后得到的趋势分量,则可以选用经典的时间序列算法.而Prophet模型的建立恰恰是基于数据中存在的周期性、季节性等不同模式,因此选用Prophet模型处理分解后的趋势分量.

本文创新性地将Informer模型与Prophet模型结合应用于太阳电池阵参数趋势预测问题,以过去48 h的某太阳电池阵的6个维度数据进行分析,实现同时输出多变量的趋势预测.为了进一步提高预测精度,并考虑到神经网络对于非线性特征能够很好拟合而对于趋势性特征拟合效果较差的问题,首先对各个参量进行STL分解,对分解得到的趋势分量(体现参量趋势性)采用Prophet模型预测,周期性和残差分量(非线性)采用Informer模型预测,最终相加得到预测结果.所构建的STL-Prophet-Informer模型针对数据中的趋势性项、非线性项都有很好的预测效果,能够捕获太阳电池阵多个参数之间的长期依赖信息、建模非线性关系,最终提高太阳电池阵参数的预测精度.

综上所述,由于实际卫星遥测数据存在参数众多、数据变化缓慢和趋势特征不明显等问题,在使用传统算法时容易过拟合,导致模型泛化性能不好[13],当实际遥测数据变化缓慢近似于线性变化时,LSTM网络更是无法预测.针对以上问题,本文提出了基于STL-Prophet-Informer组合模型的太阳电池阵多变量预测预测算法,对进行数据相关性分析之后的参量进行STL分解,分别针对趋势分量、非线性的周期分量和残差分量选用对应的模型进行预测,实现了对太阳电池阵多个参数的趋势预测.通过某实际卫星的数据集进行实验验证,证明了所提方法的有效性.

1 方法概述

如图1所示,基于STL-Prophet-Informer模型的多变量趋势预测方案可以分为数据预处理、STL分解和模型预测3部分.由于卫星原始遥测数据存在大量的野值,在进行STL分解之前,需要进行重采样、异常值处理和归一化等操作.然后按照数据的周期参数进行STL分解,将太阳电池阵的各个参数分解为趋势分量、周期分量和残差分量.最后使用Prophet模型预测近似呈线性的趋势分量,Informer模型预测非线性较强的周期分量和残差分量,将结果相加得到最终的输出结果.

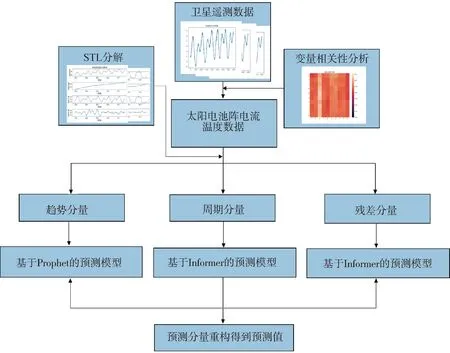
图1 预测方案流程图Fig.1 Forecast scheme flow chart

2 数据预处理

2.1 野值剔除

遥测数据在采集、传输和存储时可能由于空间环境、传输链路等原因导致存在异常信号,并且由于采样时间不匹配,会产生数据在一段时间内缺失或重复采样的情况.这些问题会干扰数据原有的特征,影响模型预测,因此需要对数据进行预处理.

本文采用LOF(local outlier factor)方法[17]进行离群点的检测.LOF核心思想即通过确定每一个数据点的局部密度值,然后对比其周围点的局部密度值,如果与其周围点的局部密度值相差较大,则判定为离群点.图2为经过野值剔除前后的对比图,从图中可以看出该算法将数据中的野值点剔除,并很好地保留了变化趋势,为后续建模提供了支持.

图2 异常值处理前后数据对比图Fig.2 Data comparison graph before and after outlier processing

2.2 数据选取

对本文所用数据集包括太阳电池阵的8个参数,分别为南北对称的两组电流、温度和转角等,对参数两两之间进行相关性分析验证,计算皮尔逊系数,绘制各参量的皮尔逊系数热力图,如图3所示.由于各个参量名称过长,这里用字母代替,由相关性热力图可知:A、B、C、D、E和F之间绝大部分的相关系数接近于±1,存在高度正、负相关性;而G、H参量的相关系数约为0,仅与自身相关.因此在模型预测时,仅选择前6个变量作为输入.

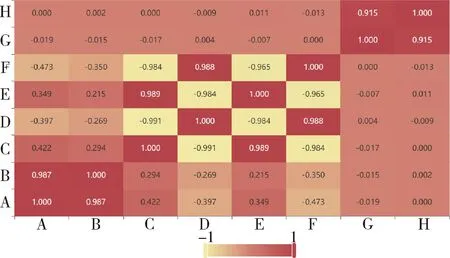
图3 各参量皮尔逊系数热力图Fig.3 Pearson coefficient heat map of each parameter

3 多变量趋势预测算法设计

本章提出的太阳电池阵多变量趋势预测的总体框架如第一节所述,即将Informer模型与Prophet模型结合应用于太阳电池阵参数趋势预测问题。为了进一步提高预测精度,并考虑到神经网络对于非线性特征能够很好拟合但对于单一增长性较强的特征拟合效果较差的问题,首先对各个参量进行STL分解,对分解得到的趋势分量采用Prophet模型预测,周期性和残差分量采用Informer模型预测,最终叠加得到预测结果。

3.1 STL分解和Prophet算法

本文选取STL(seasonal and trend decomposition procedure based on loess)[18]是因为相比于变分模态分解、经验模态分解等算法,STL分解可以将原始时间序列按加法或乘法模式分解为趋势分量、周期分量和残差分量.顾名思义,趋势分量表征序列的增长性,周期分量体现波动性,残差分量则是去除以上二者的余量.通过对某卫星遥测数据的可视化分析,太阳电池阵的各个参数以年为周期不断变化,因此这里使用STL分解更贴近实际.

其计算流程包括内外两个循环,内循环通过移动平均和Loess平滑等操作提取出原始序列中的趋势分量和周期分量,外循环通过权重调节离群值的影响,最终将时间序列分解为3个分量

y=ytrend+yseasonal+yresidual

(1)

Prophet模型的核心是对时间序列数据进行曲线拟合,其本身是一种自加性模型[11-12],模型可以由以下3个主要部分组成:

P(t)=g(t)+s(t)+εt

(2)

其中,g(t)为趋势函数,作用是对模型中的分段线性增长和非周期性变化建模,这里采用如下的逻辑回归模型:

(3)

式中,k表示增长系数,b(t)为偏置量,随着t的增加,模型容量C(t)逐渐趋于g(t).

s(t)为周期项,这里采用近似傅里叶级数的形式对周期项进行近似拟合

(4)

式中,N代表总周期数,P为某一确定的周期,a1,a2,…,aN以及b1,b2,…,bN为模型中需要估计的值.εt代表误差,这里假定其为均值为0的高斯分布.

原始Prophet模型中还含有针对节假日建模的一项,由于卫星实际运行状态受节假日情况影响极少,因此在本文的应用中不使用Prophet模型的节假日因子.

3.2 Informer模型

自从2017年Transformer 模型被提出,其在自然语言处理领域的强大建模能力使得时序数据预测问题有了更多解决方案,并且取得了不错的预测效果.尽管如此,Transformer 在长时间序列预测问题上也存在一些不足,如二次时间复杂度、编码器-解码器架构的固有限制和高内存使用率.针对这些问题,Informer[19]模型对这些不足采取了如下的改进:1)提出一种稀疏注意力机制,筛选出重要的 query,降低时间复杂度和空间的内存开销;2)提出了自注意力蒸馏机制,通过将层级输入减半来突出主导注意力,减少了维度和网络参数量,并高效处理极端长的输入序列;3)提出了生成式解码器,不需要分步操作的方式预测长时序序列,只需一步得到所有预测结果,大大提高了预测速度.

Informer模型的结构如图4所示,左侧为编码器,右侧为解码器.编码器负责提取长序列数据的特征提取,将传统的自注意力机制替换为稀疏自注意力机制[20-21].解码器接收长序列数据的输入,将目标元素使用零填充,将需要预测的全零序列也作为特征图加权注意力的一部分,接着使用生成式的方式对预测序列进行预测.

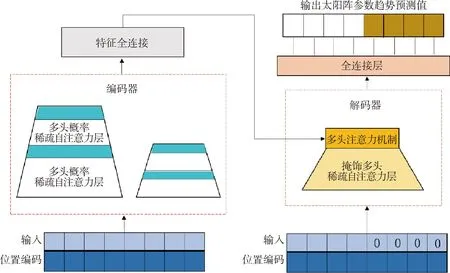
图4 Informer模型结构图Fig.4 Informer model structure diagram

将传统的自注意力机制机制[17]按比例进行缩放点积,即

(5)

其中,d是输入维度,Q∈RLQ×d代表query向量,K∈RLK×d代表key向量,V∈RLV×d代表value向量.其中key向量和value向量配对,query向量根据与key向量的运算结果查询到value向量.因此对于每一个query向量的注意力可以表示为

(6)

传统的自注意力机制在计算概率p(qi,ki)时采用的常规点积运算会达到二次时间复杂度,空间复杂度为O(LQ,LX),这在长序列的预测中会加大模型训练难度.通过对自注意力概率分布的研究发现,其注意力分数具有稀疏特性且呈现长尾分布,即注意力分数较高的点积占少数,恰是这一部分对整个注意力的影响最大,因此可以考虑忽略其余权重较小的部分,不需计算其中部分来自query向量对value向量的贡献.结合以上论述,query向量的稀疏性评价公式[22]为

(7)

其中等式右边前一项是qi在所有key向量上的LSE(log-sum-exp),第二项是算术平均.如果M(qi,K)较大,则说明该注意力分布更多变,在上面提到的长尾分布中包含注意力分数大的点积对的概率就大,基于以上分析,就可以得到稀疏自注意力公式,即只使用u个占主导地位的query向量与key向量计算点积对,公式如下:

(8)

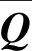
为了降低模型的时间复杂度,提出一种有效获取query向量稀疏度测量的方法,即Informer模型的 max-mean 度量

(9)

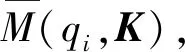
编码器部分用于在长序列输入数据中提取特征,并尽可能保持鲁棒性[23].因为稀疏自注意力机制的存在,编码器的特征映射中将不包含关于value的冗余部分,均为注意力分数较大的key-value对对应的value向量.编码器部分还利用蒸馏对具有主导地位的特征进行强化,可以在下一层稀疏自注意力中更加聚焦.在这个过程中,对于模型的输入不断减少,具体的蒸馏操作见如下公式:

(10)

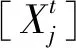
解码器部分用生成式得到长序列的预测结果,解决了数据时间复杂度较高的问题.其输入向量表示为

(11)

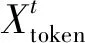
4 实验验证

4.1 实验设置

(1)STL-Prophet-Informer模型结构设置

利用STL-Prophet-Informer模型可以实现对太阳电池阵6个参数趋势变化的同时预测,为提高模型泛化性能,减少过拟合,设置Dropout为0.05,均方差为模型的损失函数.将输入数据按照7∶2∶1的比例划分为训练集、测试集和验证集.将模型的网络参数如表1所示.

表1 模型网络参数表Tab.1 Model network parameter table

(2)评价指标

为了评价模型预测精度[24],分别使用均方差(MSE)、均方根误差(RMSE)和平均绝对误差(MAE)作为评价指标,计算公式如下:

(12)

(13)

(14)

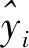
4.2 STL分解结果

某卫星的遥测数据包含太阳电池阵的6个遥测参数,数据跨度在6年左右.

考虑到卫星的轨道周期,将STL分解的周期参数设置为365天.由于太阳电池阵南北两翼呈对称结构,因此这里选用电池阵电流和温度参量进行展示,以采样间隔为1 h的某卫星遥测数据进行STL分解,结果如图5所示.

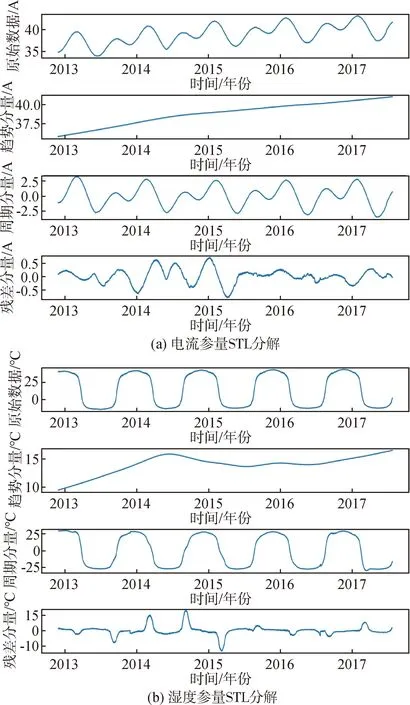
图5 太阳电池阵参数STL分解结果Fig.5 Results of STL of solar cell array parameters

4.3 实验仿真结果与分析

(1)STL-Prophet-Informer模型预测结果

通过相关性分析得到的太阳电池阵6个遥测参数中,太阳电池阵电流和温度是能够直接表征太阳帆板性能的关键参数,由于卫星的对称式结构设计,因此存在南北两组相同的参数.在这里以其中一组太阳电池阵的电流和温度为例,根据4.2的分解结果,对其中的趋势分量使用Prophet模型预测趋势,周期分量和残差分量用Informer模型预测,预测结果如图6所示.

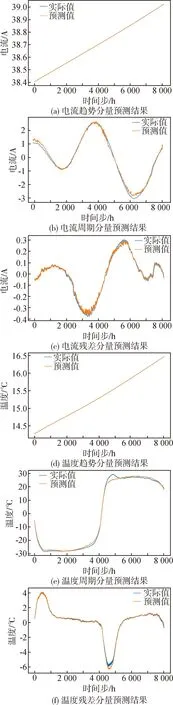
图6 太阳电池阵电流和温度各分量预测结果Fig.6 Prediction results of current and temperature components of solar cell array

通过Informer模型最后一个全连接层得到模型输出,可以同时进行多变量预测.实验以太阳电池阵的6个遥测参数的过去48 h的历史值作为输出,为了验证本文所提方法的有效性,与单一的Informer模型、LSTM模型进行对比,设置同样的输入数据长度、最大迭代次数.学习率等参数,这里依旧以其中一组太阳电池阵的电流和温度为例,各方法预测结果如图7所示.

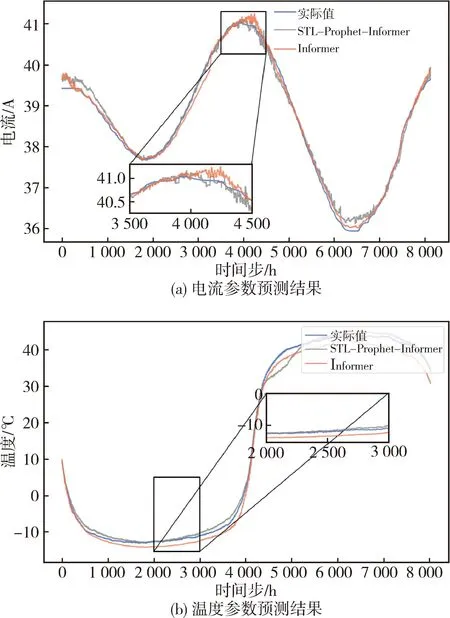
图7 太阳电池阵遥测电流和温度参数预测结果Fig.7 Prediction results of current and temperature parameters of solar array telemetry

由图7可知,相比其他方法,本文所提方法在全局内有着更高的预测精度,可以较好地跟随曲线真实波动情况,尤其在数据的趋势变化点,预测结果与实际值更为接近.分析得知,经过STL分解后的周期分量和残差分量均为非线性较强的数据,得益于Informer模型的注意力机制,可以实现较高精度的预测.部分注意力分数可视化如图8所示.

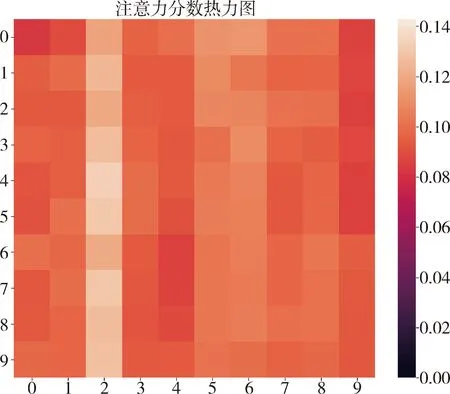
图8 多头注意力分数热力图Fig.8 Multi-head attention fraction heat map

(2)横向实验结果统计与分析

为了逐步体现本文所提方法对于多步多变量预测的有效性,首先对遥测数据A进行单步预测,即对未来一个时间步的状态进行预测.从表2可以看出,STL-Prophet-Informer模型在各项指标上表现最优,表明本文所提方法对于预测值与真实值的误差更小,预测精度更高,同时表明Informer模型相比于其他预测模型的有效性.

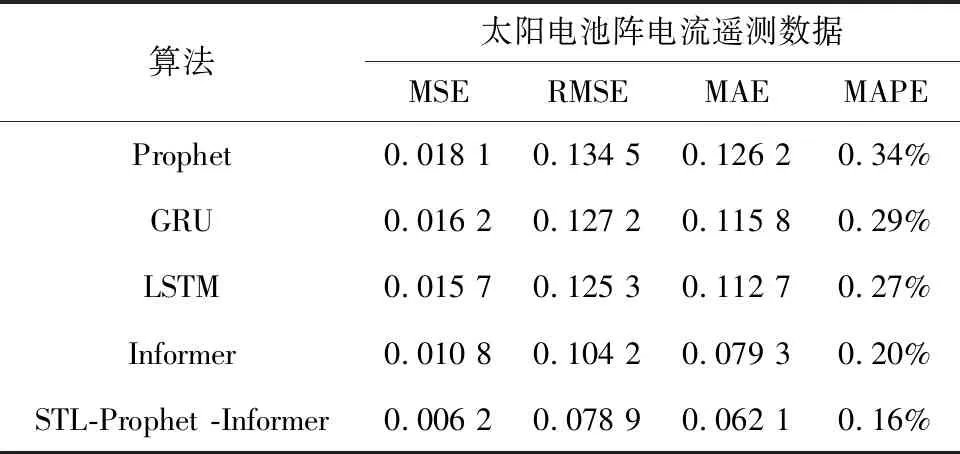
表2 横向实验结果统计表Tab.2 Statistical table of transverse experimental results

为进一步说明Informer模型在预测如周期分量和残差分量这类非线性、不平稳数据的优越性以及他相比于传统的ISTM网络更适合作为本文周期分量和残差分量的预测模型,进行多步预测实验,结果如表3所示.

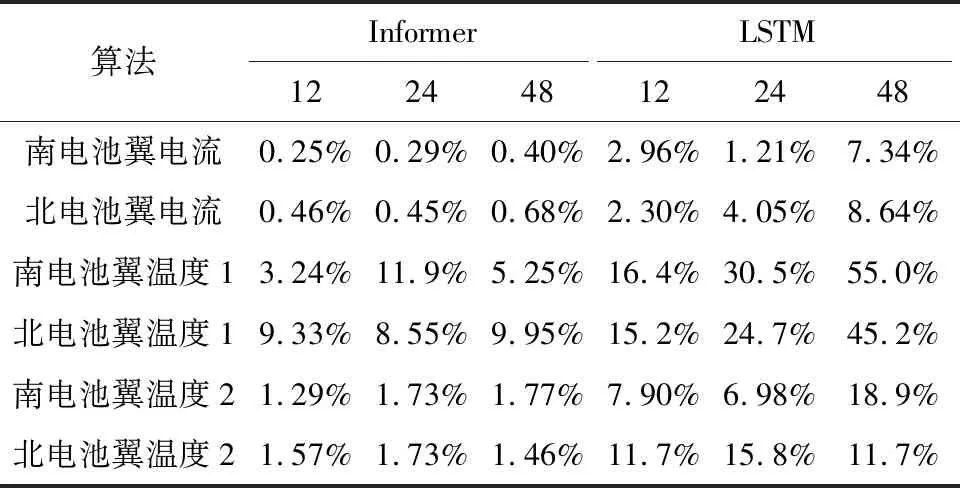
表3 多步预测实验结果统计表Tab.3 Statistical table of results of multi-step prediction experiment

(3)纵向实验结果统计与分析

为证明本文所提出的STL分解方法与Prophet-Informer模型结合的合理性和有效性,进行纵向实验结果对比.从表4试验结果可以看出:在同时使用STL分解的情况下,本文提出的方法相比于STL分解和其他模型联合应用于预测时的精度更高,提升了在趋势分量、周期分量和残差分量上的预测精度,增强了模型对于不同特征数据的泛化性能,证明了方法的有效性.

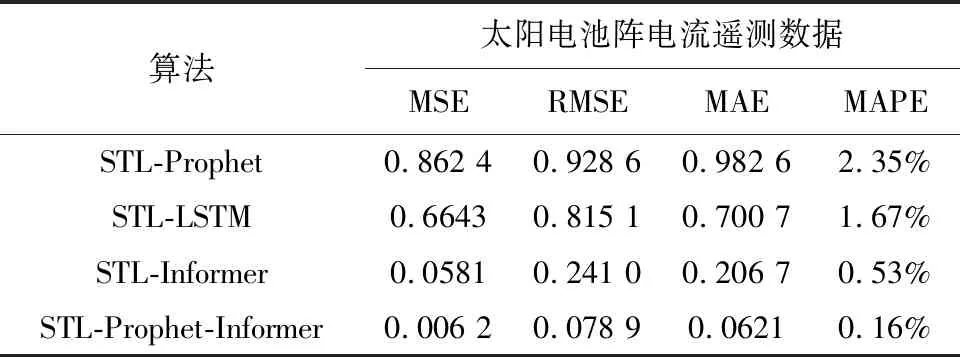
表4 纵向实验结果统计表Tab.4 Statistical table of longitudinal experimental results

5 结 论

本文提出一个基于STL-Prophet-Informer模型的太阳电池阵多变量预测预测框架,实现了对太阳电池阵多参量的趋势预测.首先对卫星遥测数据进行处理,然后利用STL分解将数据分解为趋势分量、周期分量和残差分量,最后将各分量预测结果相加后得到总的太阳电池阵参数预测值.实验结果表明,本文所提方法的MSE、RMSE和MAE优于基准模型,经过横向纵向实验对比,证明了所提方法的有效性.后续研究将考虑对更长期的参数状态进行预测,同时提高模型泛化性能,探索更高效的预测方法.