基于需求响应的电热综合能源市场MPEC优化

2024-03-11耿光辉曾小雨钟懿文唐霜华

黑龙江科技大学学报 2024年1期

杨莹, 耿光辉, 曾小雨, 钟懿文, 唐霜华

(黑龙江科技大学电气与控制工程学院, 哈尔滨 150022)

0 引言

为有效提高能源利用效率,将多种形式能源引入到电力系统中,综合能源的统一优化调配是未来新型电力系统发展的必然趋势[1]。针对以能量枢纽(EH)为纽带的电、热联合调度的供能形式,深入挖掘电、热等不同形式能源之间的耦合关系[2],充分考虑电、热综合需求响应(IDR)运行机制,增加综合能源市场(IEM)的灵活性和经济性[3],是提高新型电力系统综合能源利用效率的有效手段。

由于不同的基础设施之间具有相互依赖性,国内外学者致力于研究具有EH和多载体能量流的集成系统的建模、规划和运行。Wang等[4]将多能源系统与EH相结合使用图论自动构建EH的耦合矩阵,建立能量流模型。Moeini等[5]提出能量流多能源载体的优化和建模分解框架,通过鲁棒优化解决大规模非线性问题,实现多个EH系统能量流的整合。帅航等[6]在气电联合系统中引入需求响应,并提出了基于近似动态规划算法的联合系统经济调度策略,协调电气供需两侧供能,提高能源利用效率。崔杨等[7]在源侧利用风电给地源热泵供电,并在考虑负荷侧需求响应,提高系统风电消纳能力的同时,降低了系统的运行成本,达到了良好的社会经济效益。

笔者针对以EH为枢纽的电、热综合能源系统,采用第三方独立运营方式,以EH为领导者,将引入需求响应机制的区域配电网(PDN)和区域供热网(DHN)视为跟随者,通过主从博弈策略协调各方利益。利用IEEE标准电网和巴厘岛热网系统进行仿真,验证所建IEM模型的灵活性和经济性。

1 电热综合需求响应模型

IDR利用不同能源的特性,通过多能互补充分发挥所有用户对能量需求的时移能力,提高能源系统的灵活性和可靠性。文中采用价格型需求响应,将可削减负荷(CL)和可转移负荷(SL)与电热系统相结合,构建需求响应模型[8]。

1.1 电负荷SL型需求响应模型

SL是指用户可以根据自身需求响应电价,对工作时间进行灵活调整的负荷[9]。在一定时间范围内,总能耗近似不变,但可以进行时间上的平移调节。文中电负荷建模采用弹性矩阵法的SL型需求响应,其中弹性系数ε构成价格弹性矩阵E,可以表示为

(1)

(2)

式中:P、ΔP——发电量和电量的变化量;

D、ΔD——电价和电价的变化量。

电负荷需求响应模型为

(3)

式中:PSL0,t、PSL,t——SL前、后的电负荷;

ESL(t,j)——SL价格需求弹性矩阵。

1.2 热负荷CL型和SL型需求响应模型

CL是指用户根据价格信号和自身需求从而选择部分中断或增加的负荷。文中热负荷建模采用弹性矩阵法的CL型和SL型需求响应。其中,SL型需求响应模型原理与电负荷相同,CL数学模型为

(4)

式中:HCL0,t、HCL,t——CL前、后的热负荷;

ECL(t,j)——CL价格需求弹性矩阵。

2 需求响应机制下IEM优化模型

2.1 主从博弈的IEM架构

电热综合能源市场架构,如图1所示。

图1 电热综合能源市场Fig. 1 Integrated electric heating energy market

利用EH的电热联供与电热联储能力,将具有不同能量特性的PDN和DHN连接形成一个综合体[10]。EH内含热电联产单元(CHP)、热泵单元(HP)、储电单元(ESU)、储热单元(TSU)。PDN和DHN分别由配电网和热力网络构成,PDN和DHN的能量来源分别为燃气机组(GT)和燃气锅炉(GB),并且由EH组织协调PDN和DHN进行电热联供。优化调度中,将EH视为独立的市场运营主体,具备参与PDN和DHN中电热两个能流的交易功能,通过与跟随者PDN、DHN以电能和热能报价结算方式清算,使EH的获得收益,实现系统电能与热能的互补,促进电热能流互补消纳。

PDN和DHN分别根据电力潮流和热力潮流问题进行清算,以最小化生产成本分别出清(pgb、pdb、hb);EH通过预测清算的结果分别向PDN和DHN上报竞标价格与数量(ξb、b、ζb、pgbm、pdbm、hbm),就此完成交易。现有的热力设备和热力技术不足以支撑EH与DHN之间热能的双向交易,且热能有着易储不易输的特点,因此文中的EH与DHN之间热能为单向交易。

2.2 EH与PDN、DHN的MPEC调度模型

由图1可知,EH提交各自市场电能和热能的数量和价格,根据报价进行支付。高峰和低谷时段的不同能源价格催生套利机会。EH通过均衡约束的数学规划模型(MPEC)最优投标寻求最大利润[11],目标函数为

max(ζb)Thb+(ξb)Tpgb-(χb)Tpdb-(γ)Tpgas,

(5)

式中:ζb、hb——EH卖给热力市场热价、热量;

ξb、pgb——EH卖给电力市场电价、电量;

b、pdb——EH买入电力市场电价、电量;

γ、pgas——EH消耗天然气价格、数量。

约束条件由竞标标底,EH运行,电市出清和热力市场出清组成。从博弈论的角度来看,电力市场出清可以被视为Stackelberg博弈,其中,EH的最优策略和两个市场的出清结果即为该博弈的均衡。

EH实际的功率输入与功率输出由电、热力市场竞标结果决定的,其竞标标底约束为

pgb,min≤pgbm≤pgb,max,

pdb,min≤pdbm≤pdb,max,

hb,min≤hbm≤hb,max,

式中:pgbm、pdbm——EH向电力市场上报的竞标标底的出售或购买的最大功率;

hbm——EH向热力市场上报的竞标标底的最大供热功率。

2.3 约束条件

2.3.1 EH运行约束

文中采用的EH结构如图2所示。EH的电力、天然气输入由上级提供。输出端连接PDN和DHN,可以向PDN和DHN出售电能和热能。电能可用于ESU充电,或由产生热量的HP消耗;天然气输入到CHP中输出电和热,必要时将热能储存在TSU中。EH内部电热功率平衡、EH电功率需求和EH内置ESU与TSU充放电约束具体详见文献[10]。

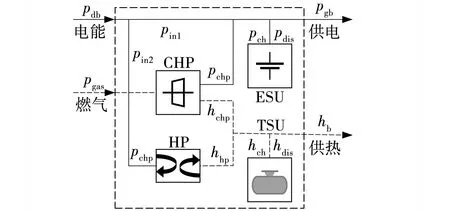
图2 EH结构Fig. 2 EH structure

2.3.2 电力市场出清

文中采用辐射式区域供电网络,结构如图3所示。将其用Dist Flow进行建模[12-13]。

图3 辐射状配电网结构Fig. 3 Structural of radial distribution network

电力市场以最小化成本为目标,其表达式及相关约束为

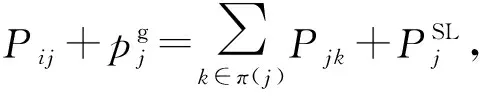
式中:aj、bj——燃气机组成本系数;

Pij、Qij——配电线路有功、无功功率;

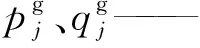
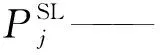
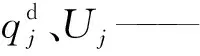
U0——节点电压幅值的平方;

rij、xij——线路电阻、线路电抗。

各条约束分别表示节点的有功平衡方程、无功功率平衡方程和节点电压方程。

2.3.3 热力市场出清

DHN通常由热源、热负荷及具有相同拓扑结构的供水网络与回水网络组成,如图4所示。

图4 DHN结构Fig. 4 Structure of DHN

由热力分布和水力分布构成的工质流模型描述供回水温度、质量流率等热网潮流信息。水由热源加热并注入供水管道;在某个节点,热水从供应侧流向返回侧,热能由热交换器取出并输送到用户;在返回侧,温度相对较低的水则被送回热源。

热力市场以最小化成本为目标,其表达式及相关约束为

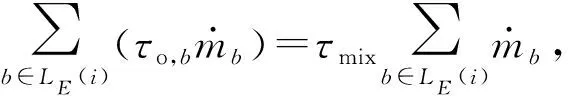
式中:αj、βj——燃气锅炉成本系数;

cp——水的比热容;

τi、τo——管道的入口、出口温度;

τmix、τam——混合流体温度、环境温度;

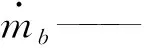
λb——管道b的温度损耗系数;

lb——管道b的长度;

h——供热功率需求;

τS、τR——供、回水侧的温度,τS>τR始终成立。

各条约束分别表示供回水侧的节点温度混合(质量守恒)方程、供回水管网节点温度、经过供回水侧管网引起的温度损耗和供热网络中热功率约束。

3 MPEC近似混合整数线性规划

将市场的清算问题写为紧凑模型可表示为

式中:q——发电调度或供热调度与EH的能量交易;

Q——发电、供热的成本系数;

c——EH上报市场的价格竞标标底。

在求解过程中,市场出清问题属于凸二次规划,其KKT系统是充要条件。利用KKT最优性条件代替,将其转化为单级优化问题,则可表示为

(6)

(7)

μT(Cq+Dx-d(pgbm,pdbm,hbm))=0,

(8)

式中:A、B、b、C、D——常系数矩阵;

x——其他变量;

d——EH上报市场能量竞标标底pgbm、pdbm、hbm;

λ、μ——等式约束与不等式约束的对偶变量。

式(6)表示原始条件的可行性约束;式(7)表示朗格朗日求偏导;式(8)表示互补松弛条件。

针对目标函数中(ξb)Tpgb、(ξb)Tpdb、(ζb)Thb等两个连续变量的双线性乘积项,文中采用布尔展开法进行线性化[14]。为不丢失电热量的最优解,对竞标价格进行布尔展开。因此目标函数(5)线性化后得:

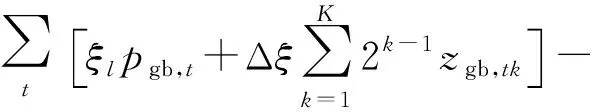
4 算例分析

4.1 算例说明

文中采用改进的IEEE-33节点PDN与巴厘岛32节点DHN进行算例仿真分析,PDN与DHN之间由母线2与节点31之间的EH实现耦合。电热综合能源市场结构如图5所示。

文中所有计算均通过Matlab中YALMIP工具箱建模,并调用CPLEX求解器计算完成。系统以t为24 h为一个调度周期;以1 h为一个调度时段进行分析;采用128段离散化EH在各个市场报价。即布尔展开法中K=7。为验证所提模型,文中设置以下3种不同场景进行对比分析。场景1为夏季,不考虑需求响应;场景2为夏季,电热综合需求响应;场景3为冬季,电热结合需求响应。

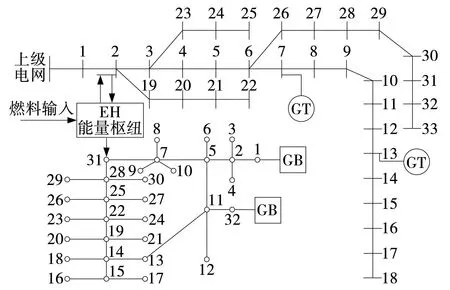
图5 电热综合能源市场Fig. 5 Integrated electric heating energy market

4.2 模型结果分析

4.2.1 场景1调度结果

夏季EH向电力市场和热力市场的竞标标底,如图6所示。EH内部储能单元的充放能情况,如图7所示。

图6 价格与数量的竞标标底Fig. 6 Base bid price of price and quantity

由图6和7a可以看出,EH的1∶00～7∶00和22∶00～24∶00时段以较低的价格从PDN中购入电能,所购电能一部分维持EH运行,一部分存储在EH内部的ESU中,用于供电高峰时段(8∶00～21∶00),实现套利运行。燃气价格便宜,EH需要大多数时段需要从燃气市场购买燃料维持自身运行且始终保持一定水平的热能输出。由图6和7b可知,HP的效率高于CHP机组,因此1∶00～4∶00时段EH的售热价格ζb比其他时段的报价低,其他时段的热能主要通过CHP消耗燃料提供。1∶00～7∶00时段和22∶00～24∶00时段EH从PDN中购入的电能一部分存储于ESU中,一部分通过热泵转化为热能存储在TSU中,以供8∶00～21∶00时段使用。从8∶00开始,电价开始上涨,EH转而使用CHP消耗天然气和发电。此外,EH的售购电标底(pgbm、pdbm)及售热量标底(hbm)与两个市场出清值相同。通过在电力市场、热力市场及燃料市场的综合交叉套利运行,在此情形下,EH的净利润达4 859.99元。系统内部各分布单元出力情况,如图8所示。

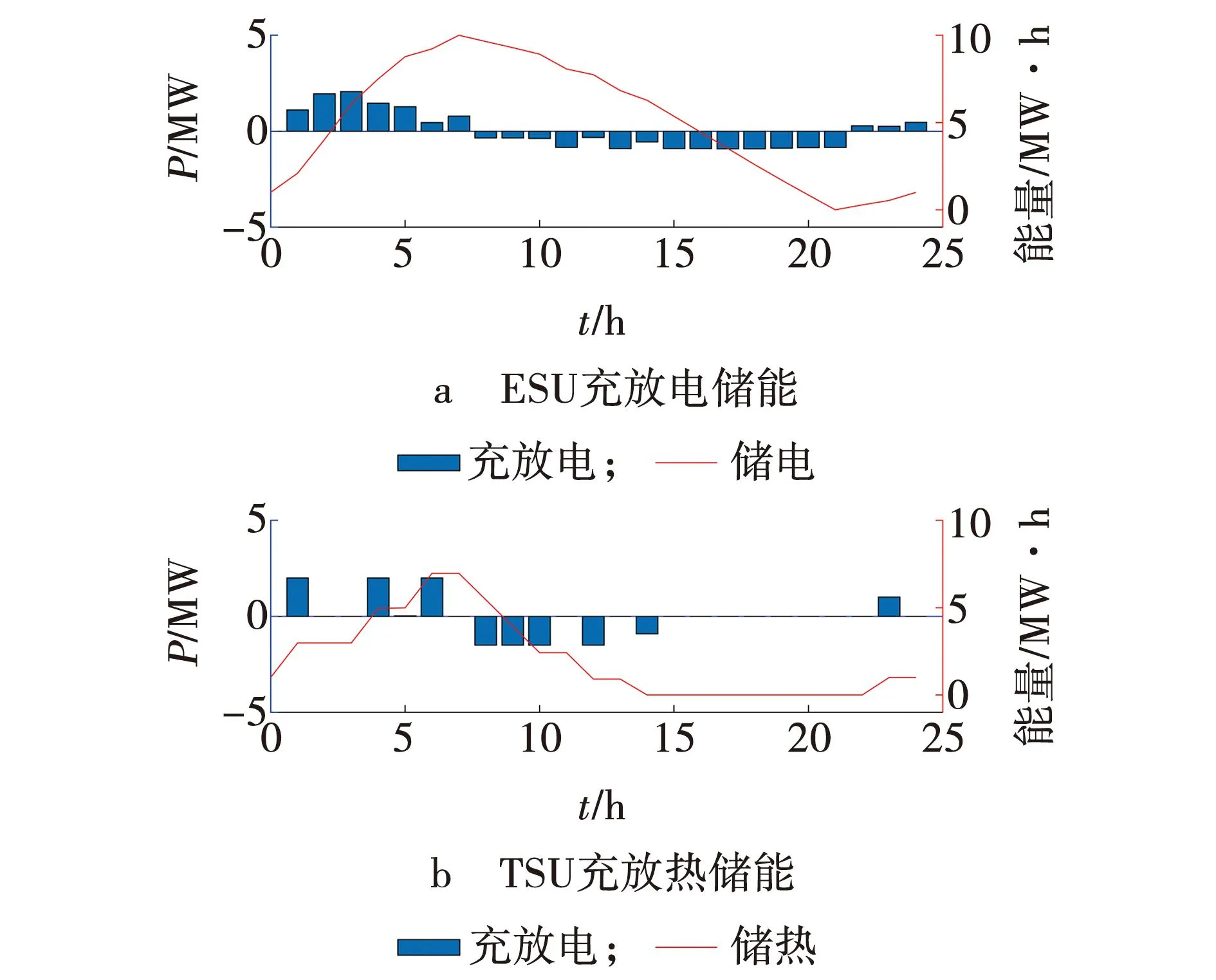
图7 EH内部储电、储热单元Fig. 7 EH internal power storage and heat storage unit

图8 场景1系统各单元出力情况Fig. 8 Scenario 1 output of each unit of system

由于电价存在波动,使得EH与PDN之间有着电能的往来交互,PDN内部的GT机组在电价高时的出力较高。EH始终保持一定水平的热能输出,并且DHN内部的GB机组一直保持一定水平的热能供应。

4.2.2 场景2调度结果

夏季负荷实施IDR后系统各分布单元出力情况如图9所示。

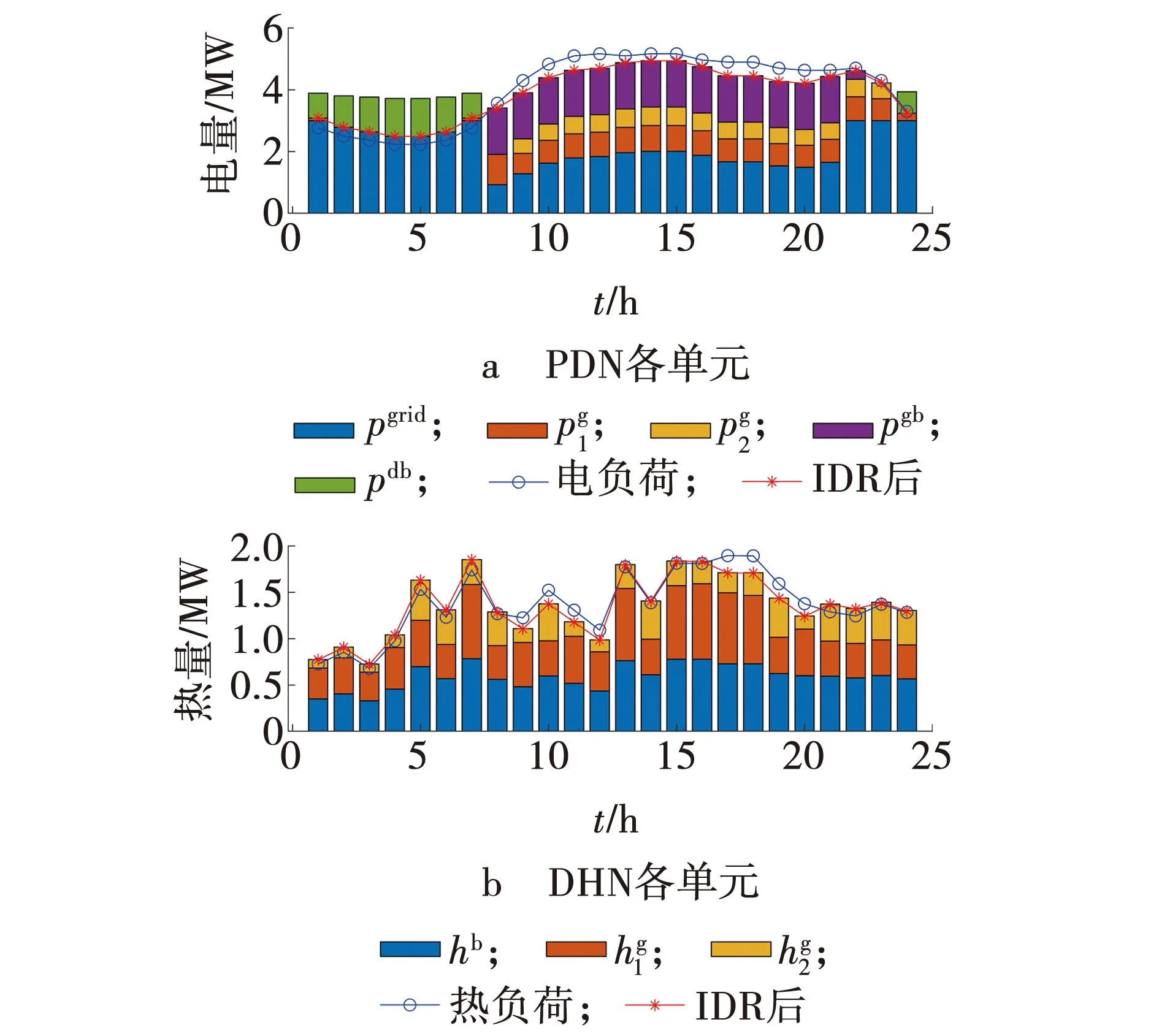
图9 场景2系统各单元出力情况Fig. 9 Scenario 2 output of each unit of system

与场景1相比较可知,PDN和DHN两侧负荷参与IDR后,均在弹性矩阵的引导下改变负荷曲线,与EH协同作用减小负荷峰谷差,曲线变得平滑。

4.2.3 场景3调度结果

冬季负荷实施IDR后系统各分布单元出力情况,如图10所示。

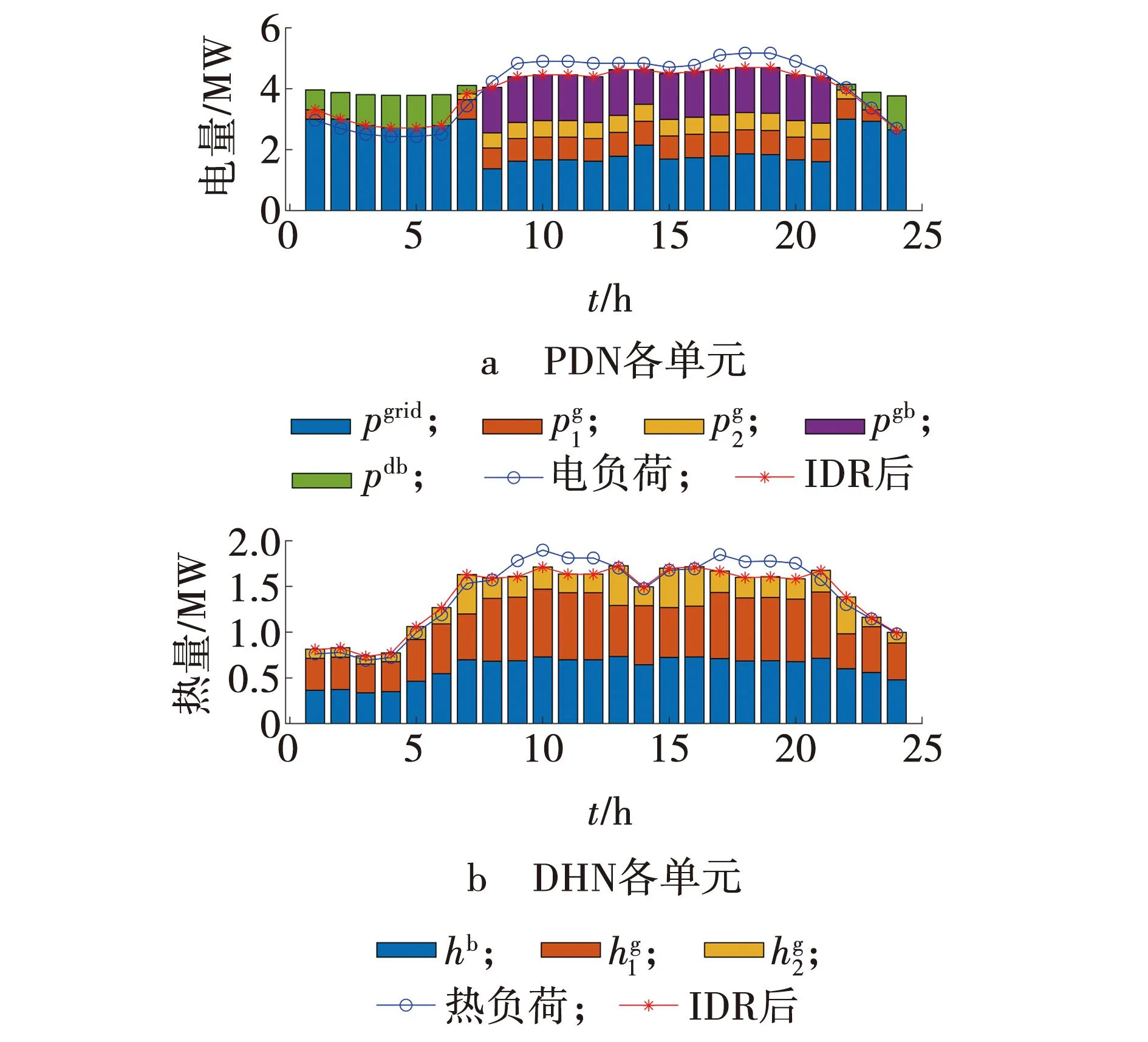
图10 场景3系统各单元出力情况Fig. 10 Scenario 3 output of each unit of system

与场景2比较可知,负荷需求在冬夏不同的季节有较大的差别。由于夏季的温度较高,空调负荷等的启动使得电需求增高;冬季的温度较低,DHN侧的热负荷增加,对于热能的需求量增加,从而EH向DHN供给的热量增加,各燃气锅炉的出力也相应增加,冬季热负荷更加平缓。

4.3 系统收支与能耗分析

系统在不同场景下购电成本(G1)、燃气成本(G2)、售电收入(S1)、售热收入(S2)、EH收益(S)如表1所示。系统在不同场景下上级电网购电量(α1)、GT耗能(α2)、GB耗能(α3)、购气量(α4)如表2所示。

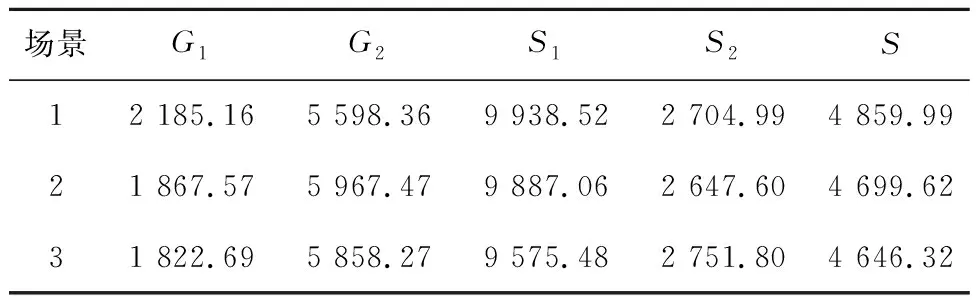
表1 各场景的收支情况

表2 系统耗能

比较场景1、2可知,在实施IDR后,在24 h内EH的收益减少160.44元,能耗减少2.3 MW。比较场景2、3可知,在IDR作用下不同季节对于收益和能耗影响不大,系统实施IDR后用能高峰时段系统内的电能和热能总需求下降,低谷时段用能量增加,整个调度周期中用能更加平均,系统的电能和热能套利收益减少。EH收益和系统整体能耗百分比变化较小,分别为3.42%和0.604%,提高了系统运行可靠性。

综上所述,考虑IDR的IEM具备了电热联供与电热联储的能力,具备了供能灵活性,获得了经济效益的同时提高了系统供能可靠性。