基于多目标优化的采煤机截割最优运动参数匹配策略

2024-03-11郭殿林

黑龙江科技大学学报 2024年1期

郭殿林, 岳博

(黑龙江科技大学电气与控制工程学院, 哈尔滨 150022)

0 引言

滚筒式采煤机作为开采煤矿的主力机械,在采煤过程中主要承担破煤和装煤两大任务。当前采煤机大多是以恒功率进行截割控制,牵引速度无法根据现场煤岩的实际工况给出最合适的大小,很容易影响采煤机的整机性能,使采煤机难以处于最佳的工作状态。

针对此问题,国内外很多学者进行了研究,葛帅帅等[1]利用遗传算法得到不同工况下最优的运动学参数,降低了齿轮动载荷,提高了采煤的经济性能。赵丽娟等[2]采用改进的MOGWO算法获得了最优决策方案,构建了自适应控制系统。金忠峰[3]利用牛顿—拉格朗日法对最优运动学参数进行了求解。施磊[4]通过改进粒子群算法求解不同工况下的最优运动参数,以协同调速截割煤岩,提高了采煤机的综合性能。张波[5]采用Matlab中的Optimization工具箱选取内点算法对采煤机最优截割性能函数的约束优化进行求解,证明了系统协同控制的有效性。但以上研究仅考虑了随截割阻抗对运动学参数的影响,而未考虑截割深度的影响,未分析不同运动参数控制下采煤机截割性能。笔者通过建立滚筒性能指标的数学模型,以不同性能指标综合最优构建目标函数,采用SA-PSO算法优化运动参数最佳匹配关系,对A-h-v曲面和A-h-n曲面进行拟合,分析采煤机在受到截割深度及截割阻抗变化的影响时牵引速度和滚筒转速的最优值。

1 截割性能多目标优化模型的构建

1.1 滚筒性能指标的数学模型

采煤机滚筒的截割性能指标一般包括生产率、块煤率、截割比能耗和装煤率等。根据文献[1]和[4],实际生产率的数学模型为

Q=10-6khDvγ,

式中:k——实际连续工作系数;

h——采煤机平均截深,mm;

D——滚筒直径,mm;

v——牵引速度,m/min;

γ——煤的容重,t/m3。

块煤率的数学模型为

式中:α——滚筒螺旋叶片的升角,rad;

φ——煤体破碎时的崩落角,rad;

N——滚筒螺旋叶片头数;

n——滚筒转速,r/min。

截割比能耗的数学模型为

式中:K——考虑煤的压张情况、脆塑性、截割条件等参数的修正系数;

Ap——截割阻抗,N/mm;

m——滚筒每条截线上的截齿数;

bp——截齿的齿刃宽度,mm。

理论装煤量为

式中:Dy——叶片直径,mm;

Dg——筒毂直径,mm;

Z——叶片头数;

δ——叶片厚度,mm;

L——叶片导程,mm;

β——叶片(中径)螺旋升角,(°);

ψ——充满系数;

Dcp——叶片中径,mm;

ρ——煤与叶片的摩擦角,(°)。

理论落煤量为

Qt=Dhvλ,

式中,λ——煤岩的松散系数。

则理论装煤率的数学模型为

1.2 目标函数的构建

针对滚筒性能指标,建立关于牵引速度v和滚筒转速n的函数为

X=[x1,x2]T=[v,n]T。

文中四个滚筒截割性能指标中,以截割比能耗最低、其他三个指标最大为目标,通过归一化的方法得到总的目标函数为

minF(X)=λ1[-Q(X)]+λ2[-S(X)]+λ3Hw(X)+λ4[-η(X)],

式中:λ1——生产率的权重系数;

λ2——块煤率的权重系数;

λ3——截割比能耗的权重系数;

λ4——装煤率的权重系数。

依据文献[6],基于企业生产要求、经济指标和经验的考量,着重关注生产率和装煤率的影响,块煤率和截割比能耗属于次要考虑因素,确定λ1、λ2、λ3和λ4分别为0.3、0.2、0.1和0.4。

1.3 约束条件的建立

生产力约束为

g1=Qj-Q≤0,

式中:Qj——实际生产率;

Q——理论生产率。

装载性能约束为

g2(v,n)=Qt-Qx≤0,

式中:Qt——理论落煤量,m3/min;

Qx——理论装煤量。

截割功率约束为

式中:Mg——滚筒总力矩,Nm;

η——机械效率;

P——截割电机额定功率,kW。

边界条件约束为

g4(v,n)=Xmin-X≤0,

g5(v,n)=X-Xmax≤0,

式中:Xmin——优化变量的最小值;

Xmax——优化变量的最大值。

2 模拟退火的粒子群算法

模拟退火算法可以以一定概率下接受劣解,避免陷入局部最优,更有可能找到真正的最优解[7]。在粒子群算法的基础上,结合模拟退火算法的优点,采用基于模拟退火的粒子群算法(SA-PSO)。该算法容易实现,收敛快,精度高。其粒子的速度和位置更新公式[8-9]为

xi(t+1)=xi(t)+vi(t+1),

C=c1+c2,

式中:xi(t)——粒子在t时刻的位置;

xi(t+1)——粒子在t+1时刻的位置;

vi(t)——粒子在t时刻的速度;

vi(t+1)——粒子在t+1时刻的速度;

c1、c2——学习因子;

r1、r2——[0,1]范围内的随机数;

pi(t)——个体极值;

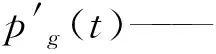
初始温度的变化公式[9]为

T=(T0,t)=T0γt,

式中:t——迭代次数;

γ——退火系数。

该算法接受劣解的概率也会随着迭代过程中初始温度的降低而不断降低。基于模拟退火的粒子群算法流程,如图1所示。

图1 基于模拟退火的粒子群算法流程Fig. 1 Flow of particle swarm algorithm based on simulated annealing

3 优化结果与分析

以MG 400/ 951型采煤机为对象,其基本参数为如下:采高范围1 150～2 300 mm,截深800 mm,摇臂长度2 855 mm,前后摇臂回转的距离6 000 mm,滚筒直径1 150 mm,单叶片齿数13,卧底量715 mm,截割功率400 kW。

采用SA-PSO算法在Matlab中进行目标函数的优化,设置初始种群大小为200,学习因子为2,初始温度为200,退温系数为0.95,最大迭代次数为500,采煤机在不同工况下牵引速度和滚筒转速最优解集如图2所示。选取截割阻抗A为100、150、200、250、300、350、400 N/mm,截割深度h为520、540、560、580、600、620、640 mm,得到49组采煤机在不同工况下最优牵引速度v和滚筒转速n,其结果如表1所示。优化结果值都在该型号采煤机参数范围之内。

表1 采煤机在不同工况下牵引速度和滚筒转速的最优值

采煤机的传统控制方法是恒功率法,牵引速度受截割功率的限制而随截割阻抗不断变化,采煤机分别在传统运动参数和最优运动参数控制下各性能指标的比较,如图3所示。

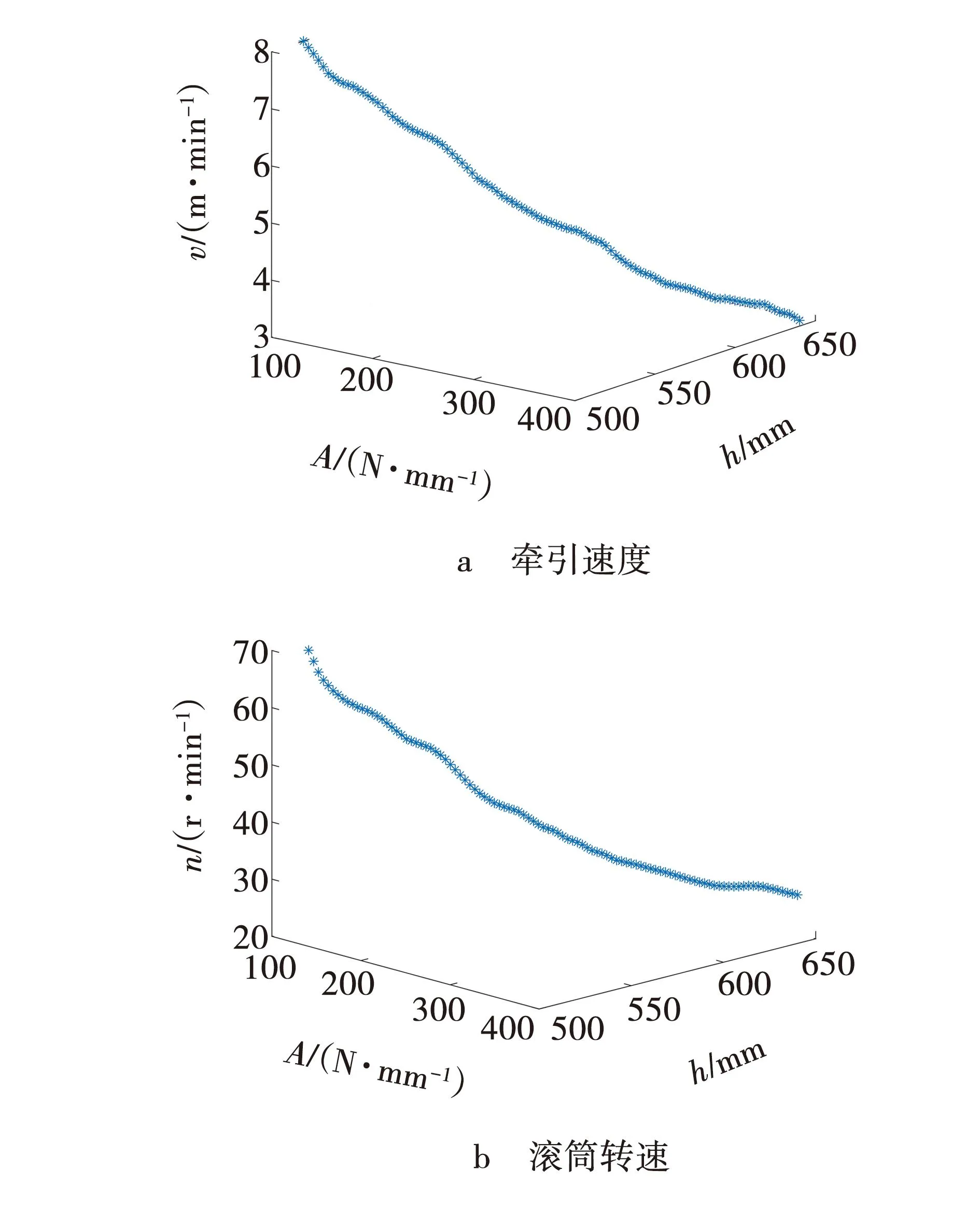
图2 不同工况下牵引速度和滚筒转速最优解集Fig. 2 Optimal solution set of traction speed and drum speed under different working conditions

由图3 a可见,两种运动参数控制下的生产率在截割阻抗较小时几乎相等,但在截割阻抗超过200 N/mm时,最优运动学参数控制下的生产率比传统运动参数控制的稍低。由图3 b、d可知,在模拟的工况条件下,优化后的块煤率和装煤率在任何情况下都比传统的有明显提升。由图3 c可知,两种运动参数控制下的截割比能耗在截割阻抗小于180 N/mm时几乎相等,但随着截割阻抗的增加,最优运动学参数控制下的截割比能耗开始低于传统运动参数控制,并且差距逐渐增大。由图3可见,在不同截割阻抗下,可得到不同的生产率、块煤率、截割比能耗及装煤率数据,取其均方根值,可得生产率总体降低了3.2%,块煤率整体提升了138.5%,装煤率整体提升了40%,截割比能耗整体降低了30.8%。

符合目标函数中采煤机的综合性能最优,由于实际生产率的数学模型只与牵引速度有关,因此在牵引速度下降时,生产率也会略有降低,但由于采煤机各性能指标所占权重不同,适当降低生产率可以大幅提高块煤率和装煤率,从而提高经济效益。

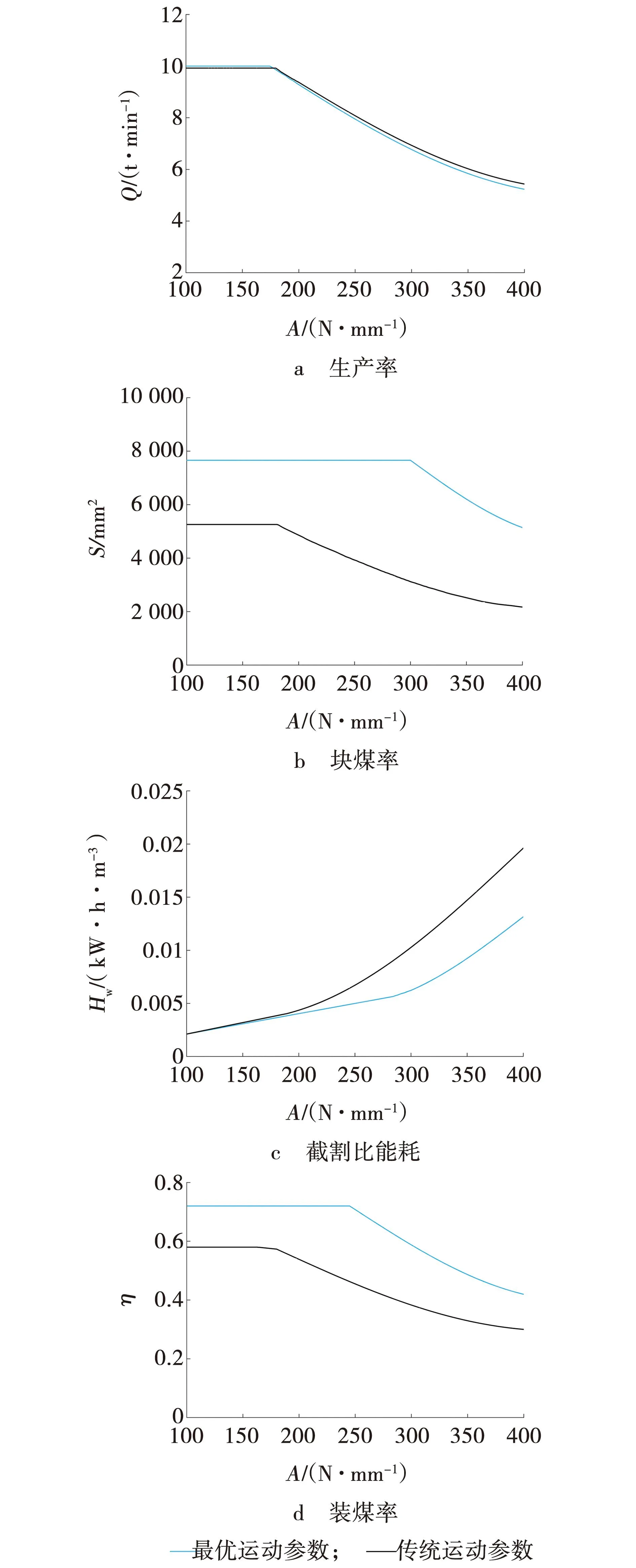
图3 不同运动参数控制下各性能指标比较Fig. 3 Comparison of performance indexes under control of different motion parameters

4 最优运动学参数匹配

4.1 曲面拟合

在Matlab中对以上49组数据分别进行A-h-v和A-h-n曲面拟合,可以分别得到其曲面拟合方程。A-h-v拟合曲面和A-h-n拟合曲面如图4和5所示。

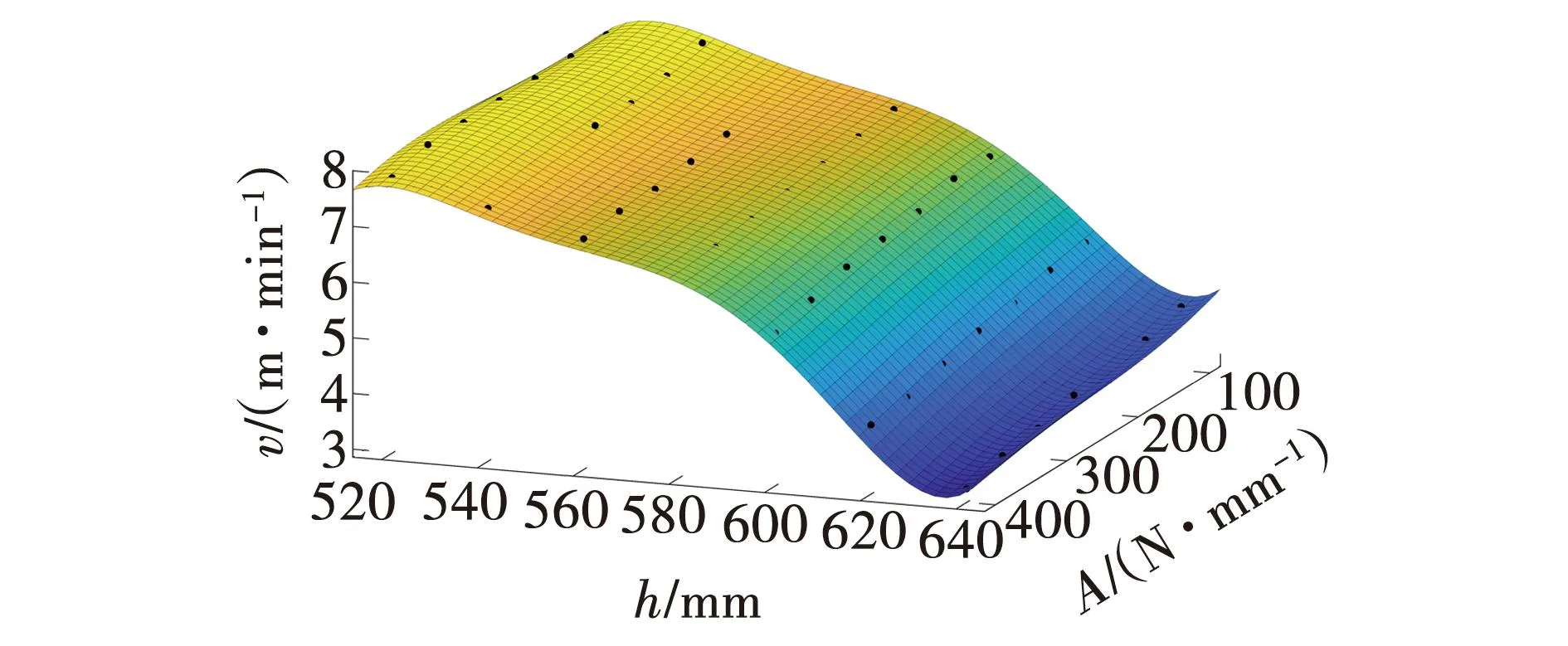
图4 A-h-v拟合曲面Fig. 4 A-h-v fitted surface

A-h-v的拟合方程为

(1)

式中,M=[E∶F]。

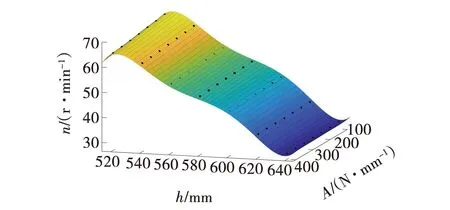
图5 A-h-n拟合曲面Fig. 5 A-h-n fitted surface

A-h-n的拟合方程为

(2)

式中,N=[G∶H]。

由式(1)和(2)可以看出,采煤机的运动学参数牵引速度v和滚筒转速n会在截割阻抗和截割深度变化时取得最优值。

4.2 最优运动学参数匹配

最优运动学参数匹配的基本流程主要包括:多目标优化、目标函数寻优、函数拟合和电机推荐转速。在Matlab/Simulink环境下搭建最优运动学参数匹配模块仿真模型,如图6所示。

图6 最优运动学参数匹配模块仿真模型Fig. 6 Optimal kinematic parameter matching module simulation model

采煤机在实际截割过程中,截割深度以及截割阻抗会发生变化,进而影响采煤机的牵引速度和滚筒转速的大小。为体现在实际工况下其变化对整体控制系统的影响,使最优电机转速生成模块前的采煤机截割阻抗A和截深h分别在100～400 N/mm和0.52～0.64 m之间不规则地缓慢增长,作为模拟实时变化的工况。模拟后的截割阻抗A和截深h随时间变化的曲线如图7、8所示。

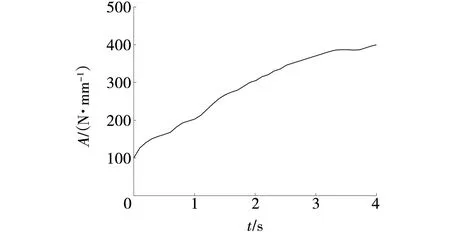
图7 模拟截割阻抗变化曲线Fig. 7 Simulate cutting impedance change curve

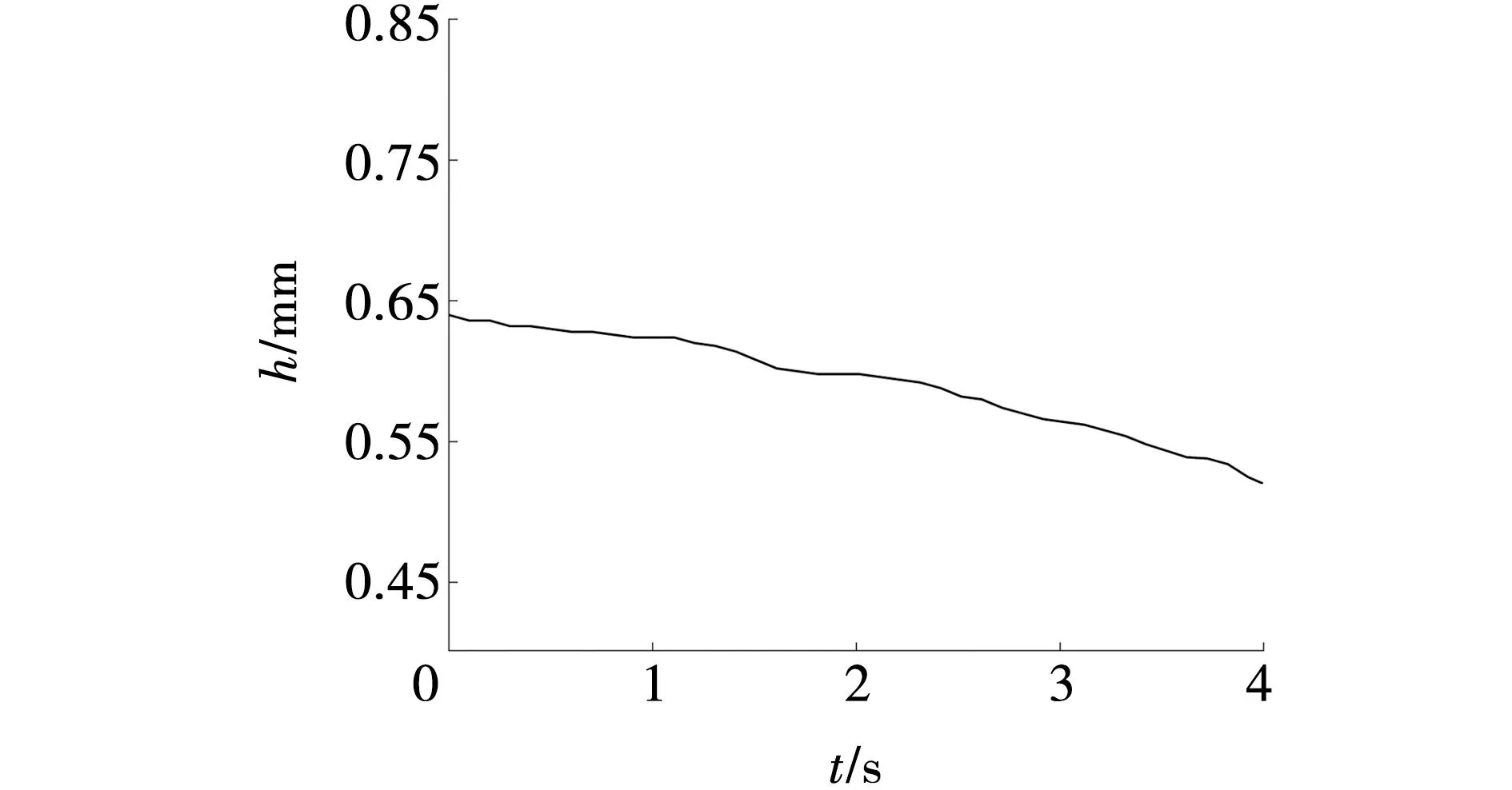
图8 模拟截割深度变化曲线Fig. 8 Simulate cutting depth change curve

最优速度推荐模块可以给出最优的牵引速度和滚筒转速,其中,牵引速度是通过传动比折算成牵引电机的推荐转速,最优滚筒转速曲线和最优牵引电机转速曲线分别如图9、10所示。由图7～10可以看出,最优电机转速曲线随截割阻抗和截割深度的增大而减小,可以使滚筒性能综合指标达到最优,使采煤机在可靠高效工作的同时减少损耗。

图9 最优滚筒转速曲线Fig. 9 Optimal drum speed curve

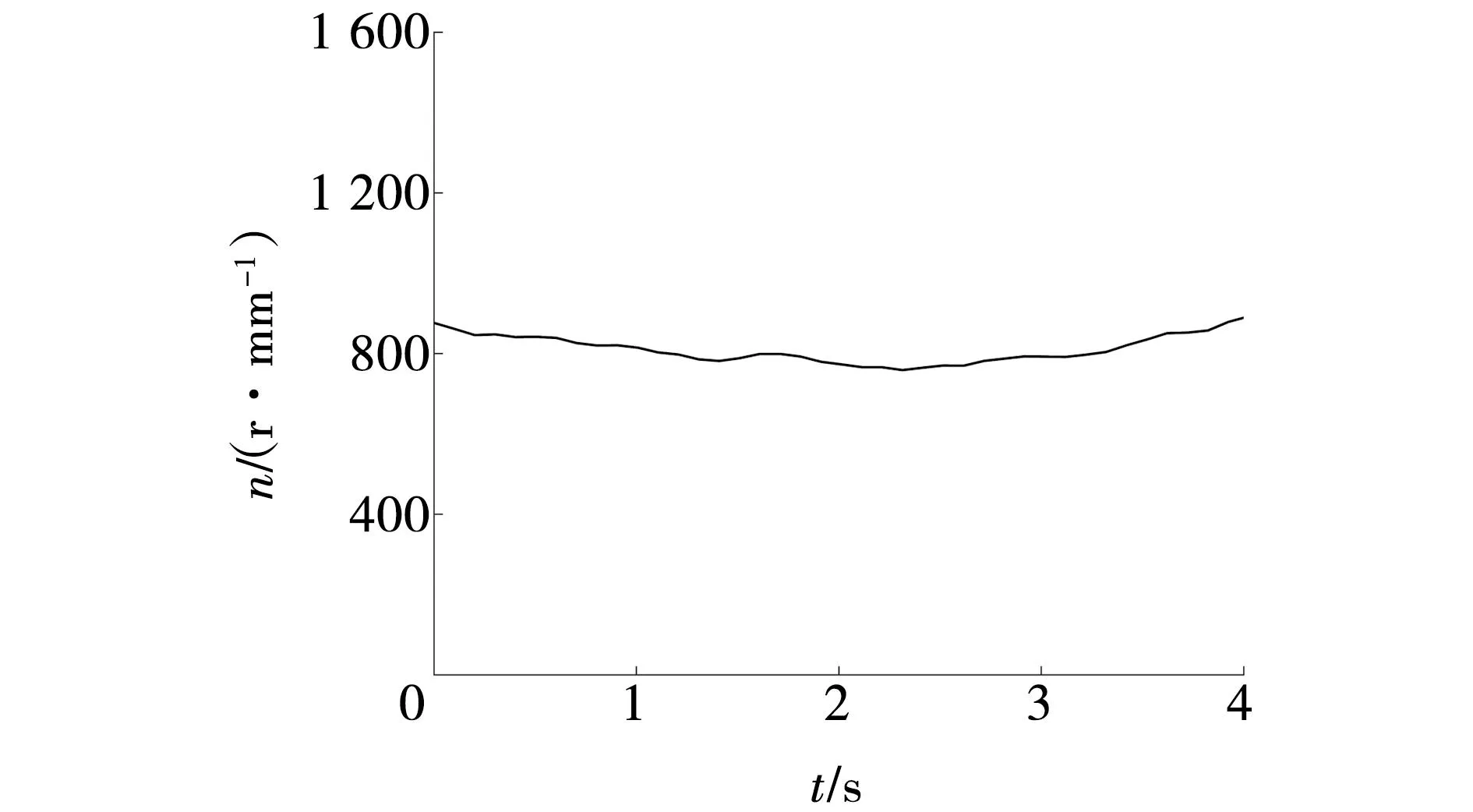
图10 最优牵引电机转速曲线Fig. 10 Optimal traction motor speed curve

采煤机在工作过程中受到总牵引阻力为

式中:μ——采煤机与导轨的摩擦系数;

G——采煤机重力,kN;

α——工作面倾角,(°);

Rx——前滚筒x向力,kN;

Rz——前滚筒z向力,kN;

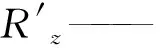
Y——前滚筒截齿的牵引阻力,kN;

Y′——前滚筒截齿的牵引阻力,kN。

牵引电机的负载转矩近似为

式中:RL——行走轮半径,m;

i——行走部整个传动系统的总传动比;

η——传动效率。

根据文献[10]的验证,给出了电机的模拟负载转矩曲线,如图11所示。

图11 模拟负载转矩曲线Fig. 11 Simulated load torque curve

在Matlab/Simulink环境下搭建采煤机截割—牵引协同控制系统的仿真模型,如图12所示。采用转速外环PI控制、转矩磁链内环的滞环控制方式,通过这一控制策略,可以得到负载转矩曲线、负载转矩误差曲线、滚筒转速曲线和牵引电机转速曲线,分别如图13～16所示。

图12 采煤机截割牵引协同控制系统仿真模型Fig. 12 Simulation model of shearer cutting and pulling cooperative control system

图13 负载转矩曲线Fig. 13 Drum speed curve

图14 负载转矩误差曲线Fig. 14 Drum speed curve

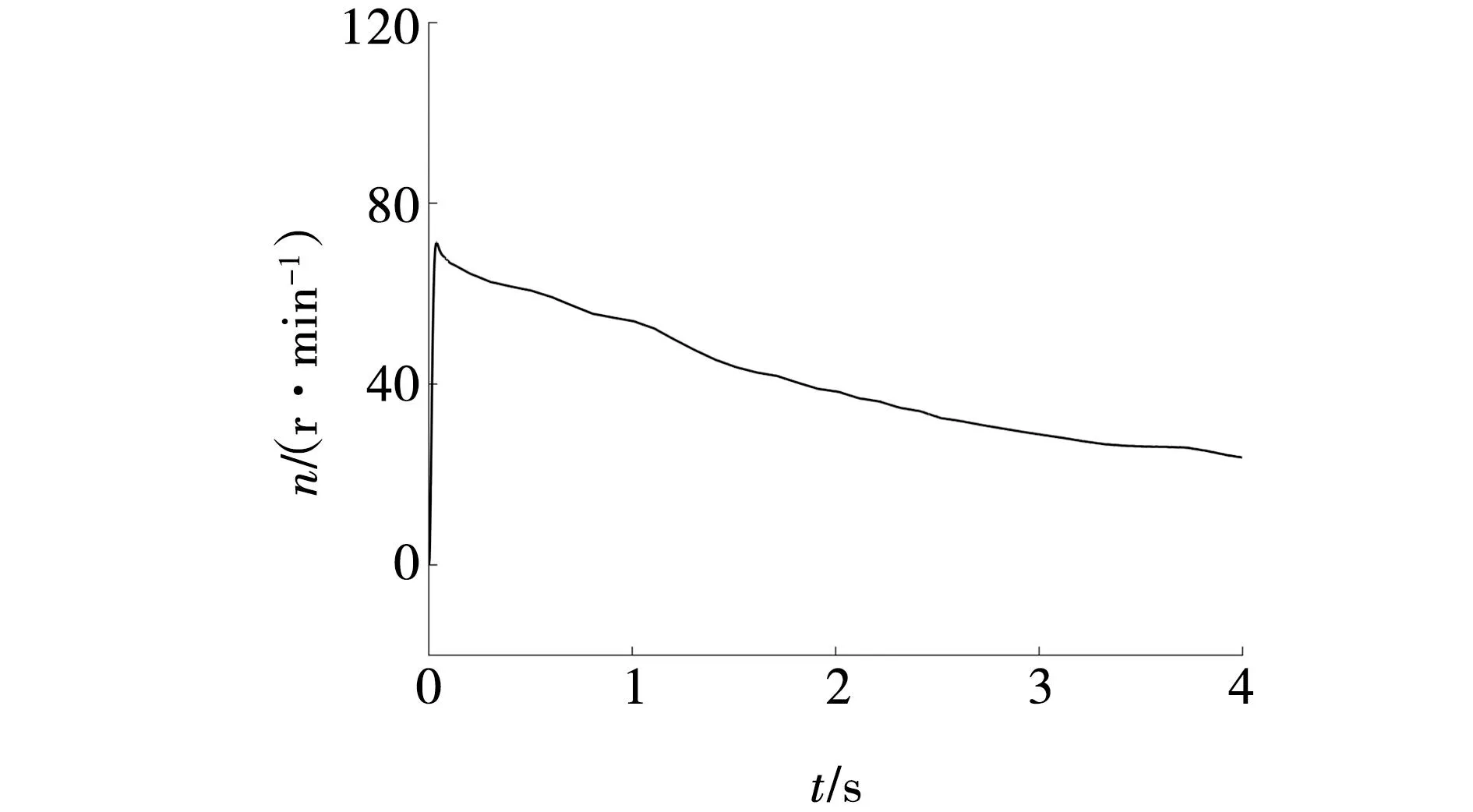
图15 滚筒转速曲线Fig. 15 Drum speed curve

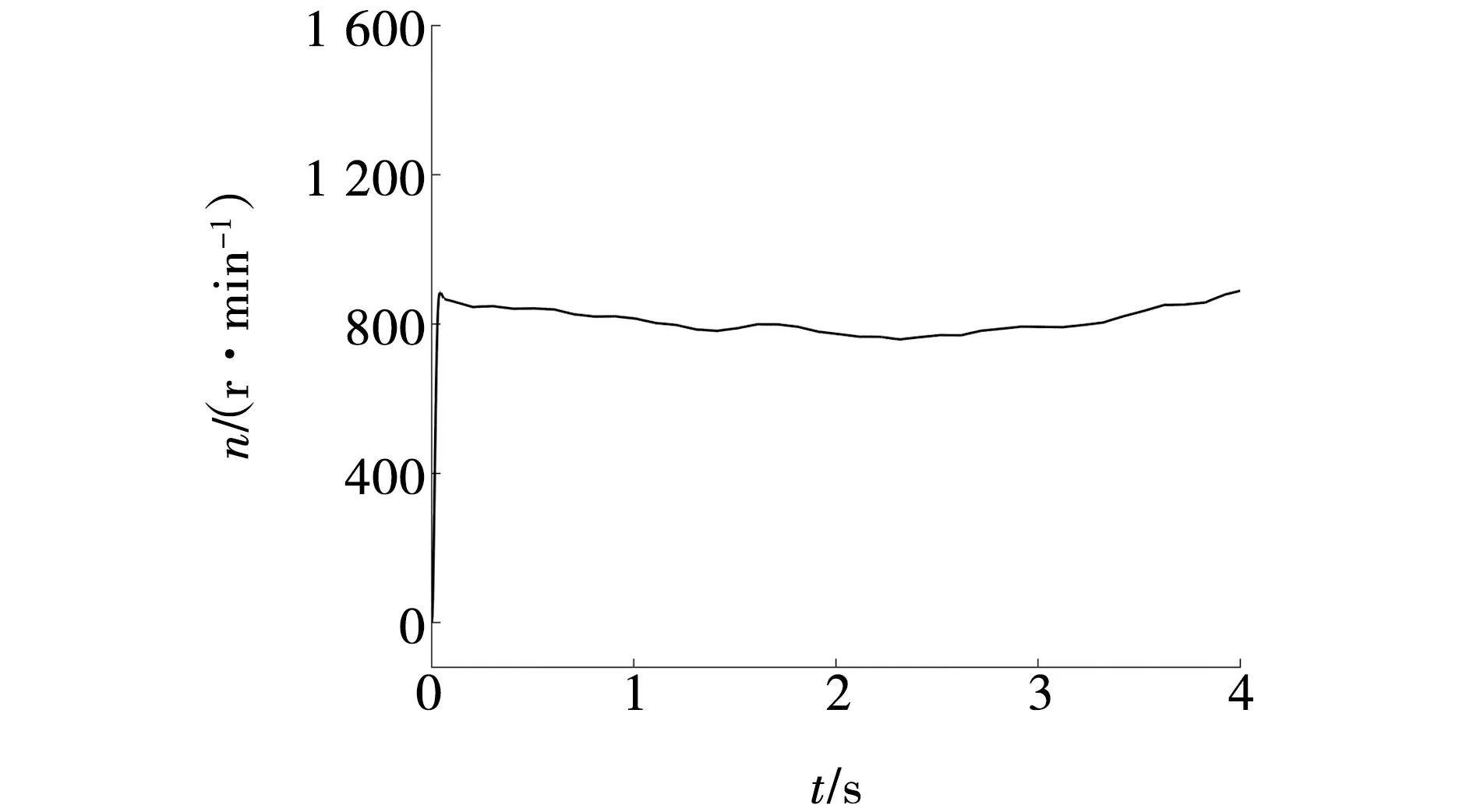
图16 牵引电机转速曲线Fig. 16 Traction motor speed curve

由图14可以看出,采煤机在0.1 s后误差稳定在1 N·m以内。由图9和15可知,在采煤机开始截割煤岩到稳定工作后,滚筒转速随A和h的变化而变化,滚筒转速曲线与推荐的最优滚筒转速曲线基本保持一致,符合预期。同理图10和16也符合预期。因此该系统能随着实时工况的变化较好地跟踪最优牵引电机转速和滚筒转速。