在线优化参数的多变量无模型预测线性自抗扰控制
2024-03-11侯小秋李丽华
侯小秋, 李丽华
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
多变量无模型预测线性自抗扰控制系统参数的在线优化可以提升系统的稳定性,相关学者研究了优化参数的线性自抗扰控制,周涛[1]利用差分进化算法优化线性自抗扰控制算法的观测器带宽和控制器带宽两个参数。唐超等[2]采用鸟群优化算法优化了线性自抗扰控制器的参数。侯小秋[3-5]提出一种具有辅助向量的时变多变量紧格式动态线性化方法,研究了多变量系统的变时滞无模型预测滤波PID控制,多变量系统的变时滞无模型自适应单值预测控制,以及多变量系统的变时滞无模型自适应广义预测控制。在上述研究基础上,笔者研究在线优化参数的多变量无模型预测线性自抗扰控制。
1 泛模型和预测模型
1.1 线性叠加非线性的模型
多变量线性模型上叠加非线性的非线性系统的状态方程,不失一般性书写简化,研究二阶时延系统,
(1)
式中:y——输出向量;
u(t)——输入向量;
x1、x2——状态变量向量;
aij、bij——时变参数;
FΔ(…)——非线性向量函数;
τ——时延;
ω(t)——干扰向量。
yT=[y1,y2,…,yn],
uT(t)=[u1(t),u2(t),…,un(t)],
式(1)x2的分量形式为
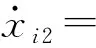
(2)
式(1)离散化为多变量NARMA模型为
y(k)=F[y(k-1),y(k-2),…,y(k-ny),u(k-d),u(k-d-1),…,u(k-d-nu+1)],
(3)
式中:y(k)——y(t)的离散值向量;
u(k)——u(t)的离散值向量;
ny、nu——阶数;
d——时延,d=round(τ/h)+1;
h——采样步长;
round(·)——取整函数。
1.2 偏格式动态线性化方法
基于文献[6]的多变量偏格式动态线性化方法和文献[3]具有辅助向量的多变量紧格式动态线性化方法,给出具有辅助向量的多变量偏格式动态线性化方法的泛模型为
Δym(k)=B(q-1)Δu(k-d)+v(k),
(4)
式中:Δ=1-q-1——加权网络;
ym(k)——泛模型输出;
v(k)——辅助向量,意义见文献[3]。
vT(k)=[v1(k),v2(k),…,vn(k)],
B(q-1)=B0+B1q-1+…+BLu-1q-(Lu-1),
(5)
式中,Lu——伪阶数。
(6)
式中,bijl——参数,意义见文献[6]。
1.3 参数估计
(7)
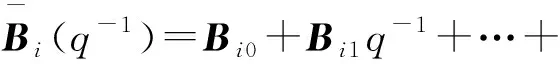
(8)
Bij=[bji1,bji2,…,bjin],
(9)
参数分量ηi向量为
(10)
则Δymi(k)关于ηi的梯度为,由式(7)得:

(11)

(12)
Δymi(k)关于ηi的二阶导数矩阵为
(13)
选取优化ηi的目标函数为
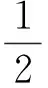
(14)
式中:Δypi(k)——实际输出分量增量;
λi(k)——对角矩阵;
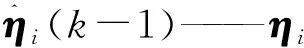
参考文献[7]的直接极小化指标函数自适应优化算法优化ηi,算法为
(15)
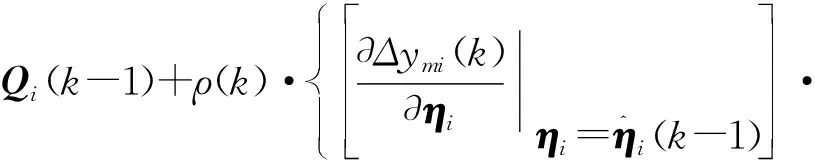
(16)
式中:ρ(k)——收敛因子;
Qi(k)——海森矩阵。
Qi(k)求逆及克服算法病态λi(k)的取值参考文献[8]的算法实现。
1.4 预测模型
由式(4)采用逐步迭代得预测模型为

(17)
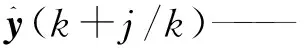
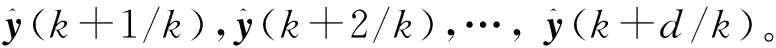
2 多变量线性自抗扰控制
2.1 多变量线性跟踪-微分器
参考输入第i个分量的线性跟踪-微分器[9],采用参考输入的超前d-1步的ri(k+d-1)构成,离散形式为
(18)
式中:Ri——速度因子;
ri(k+d-1)——超前参考输入;
vi1(k)——ri(k+d-1)的跟踪信号;
vi2(k)——ri(k+d-1)的跟踪微分信号;
fhi——线性函数。
2.2 多变量线性扩张状态观测器

(19)
式中,u0i(k-1)——虚拟控制分量。
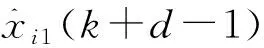
β01i、β02i、β03i由观测器的带宽ωoi确定,具体为
β01i=3ωoi,
(20)
(21)
(22)

2.3 多变量线性状态误差反馈控制律
文献[9]的多变量线性状态误差反馈控制律为
u0i(k)=kpi[vi1(k)-zi1(k)]+kdi[vi2(k)-zi2(k)],
(23)
式中,kpi、kdi——控制参数。
kpi、kdi由控制器带宽ωci进行整定,得:
(24)
kdi=2ωci。
(25)
2.4 干扰补偿控制律
u(k)=B-1[u0(k)-z3(k)+xa(k)],
(26)
(27)
(28)

2.5 总和扰动
由式(2)(19)得总和扰动第i个分量为

(29)
3 参数在线优化
3.1 ui(k)关于待优化参数向量的梯度
由上述研究可知,文中的多变量线性自抗扰控制的待优化参数向量为
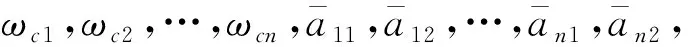
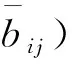
(30)
式(23)对Ri求偏导得:
(31)
其余分量为零。
由式(18)得:
ri(k+d-1)]-2hvi2(k-1)。
(32)
由式(19)得:

(33)
由式(27)得:
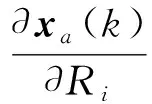
(34)
式(23)对ωoi求偏导得:
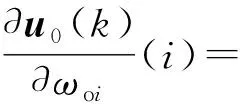
(35)
由式(19)得:
(36)
(37)
由式(20)(21)得:
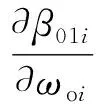
(38)

(39)
由式(19)得:
(40)
其余分量为零。
由式(22)得:
(41)
由式(27)得:
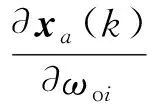
(42)
由式(23)得:
(43)
由式(24)(25)得:
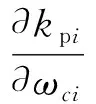
(44)

(45)
由式(19)得:

(46)
由式(27)得:
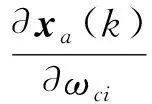
(47)
由式(23)得:
(48)
其余分量为零。
(49)
其余分量为零。
由式(19)得:
(50)
(51)
(52)
(53)
由式(27)得:
(54)
其余分量为零。
(55)
其余分量为零。
(56)
(57)
其余分量为零。
由式(17)可知,令j=d得:
(58)
由式(58)可得:
3.3 参数在线优化
采用文献[3]的多变量非线性递推最小二乘法对η进行在线优化。
目标函数为
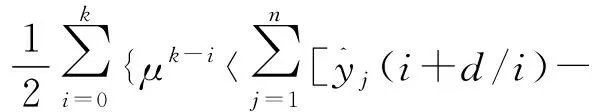
(59)
式中:μ——遗忘因子;
αj——加权因子;
λ(k)——权重对角矩阵;
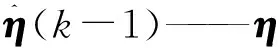
η的在线优化算法
(60)
P(k-1)=μP(k-2)+
(61)
式(60)(61)的矩阵求逆和克服算法病态的λ(t)取值参考文献[8]的算法实现。
4 仿真研究
被控对象n=2,a11=35(1+0.1t/2),a12=1 100(1+0.1t/2),a21=35(1+0.1t/2),a22=1 100(1+0.1t/2),


b11=252×2,b12=202×2,b21=152×2,b22=242×2,
τ=3h,h=0.002 5s,伪阶数Lu=2,
Q1(0)=Q2(0)=100I,B10、B11、B20、B21的初始参数略,v1(0)=0,v2(0)=0。
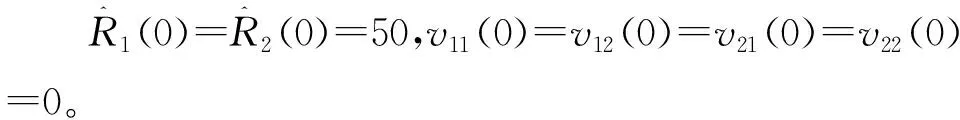
多变量线性扩张状态观测器的初始值为
z11(0)=z12(0)=z13(0)=0,
z21(0)=z22(0)=z23(0)=0,
多变量线性状态误差反馈控制律的初始值为
在线优化参数时采用多变量非线性递推最小二乘法的P(-2)=10-6I,α1=α2=1,μ=0.98。

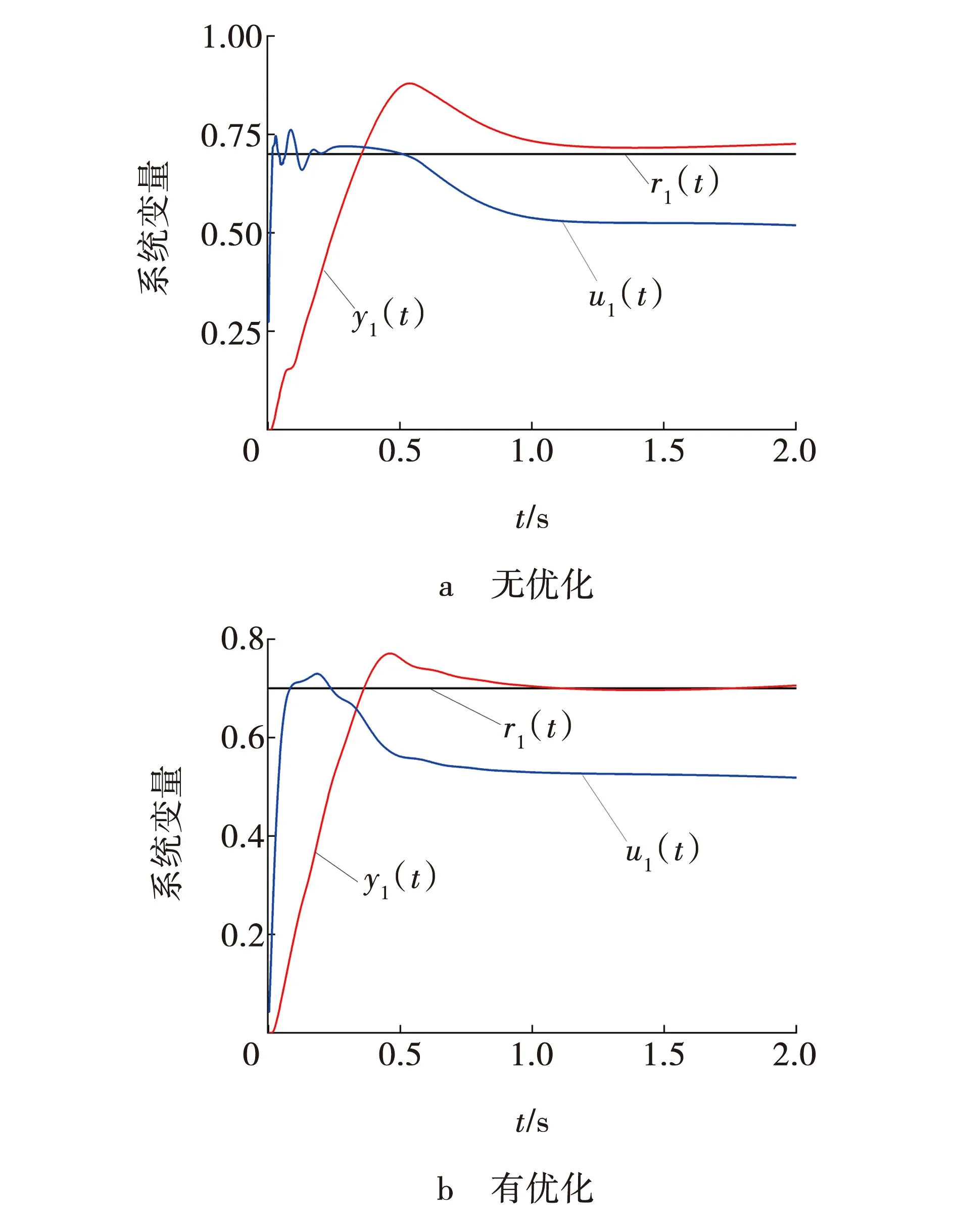
图1 响应曲线Fig. 1 Response curve
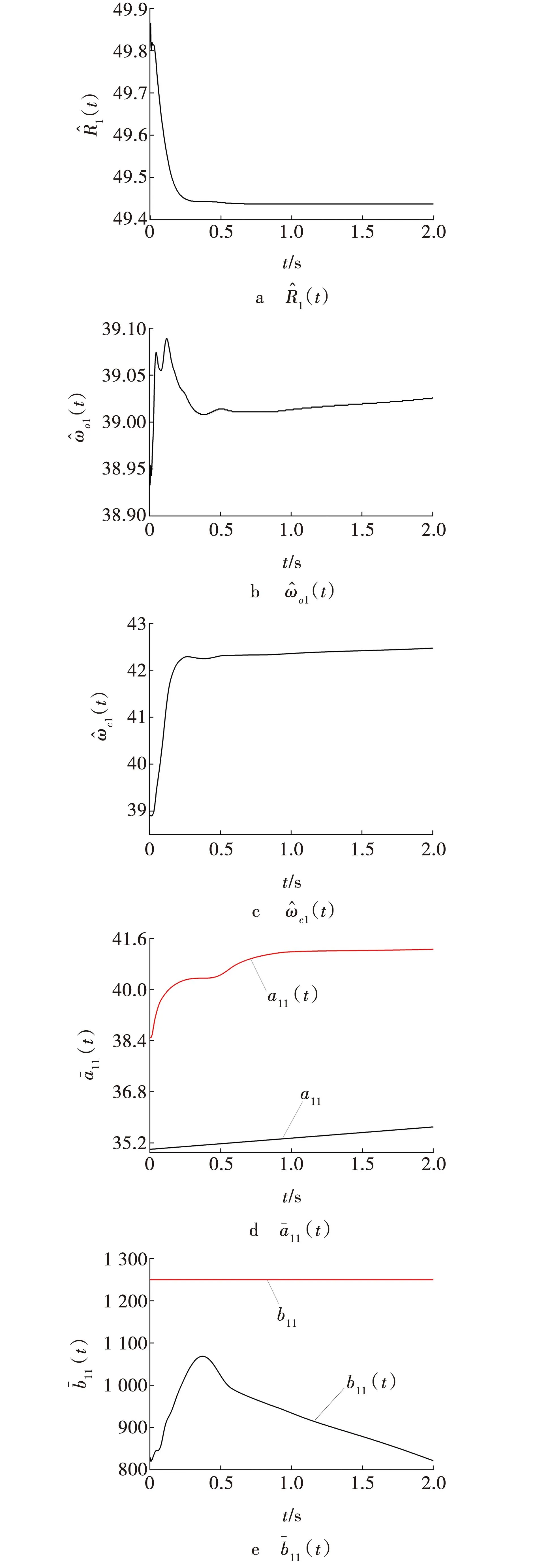
图2 参数优化曲线Fig. 2 Parameters optimization curve
5 结 论
(1)研究了基于线性模型叠加非线性的非线性系统的多变量线性自抗扰控制结合无模型控制,选取参数为零时,算法转化为适用于纯非线性系统的控制算法。

(3)使用多变量非线性递推最小二乘法对多变量自抗扰控制的参数在线优化,并同时估计线性模型的参数,算法具有自适应功能。在多变量线性跟踪-微分器中引入超前参考输入,在多变量线性扩张状态观测器中引入输出预测值,使改进的多变量线性自抗扰控制具有预测控制性能。预测模型可使用神经网络辨识的模型和NARMA-L2模型等。
