基于XALO-SVM的同步电机转子绕组匝间短路故障诊断方法
2024-03-11付强
付 强
(黑龙江科技大学 信息网络中心, 哈尔滨 150022)
0 引 言
同步电机作为电力系统中重要的设备,其运行稳定性对于电力供应的可靠性至关重要。然而,转子绕组匝间短路故障是同步电机运行中常见的问题,会导致电机输出不稳定甚至损坏电机,因此,精确检测同步电机的故障显得尤为关键[1-3]。转子绕组匝间短路故障可分为静态和动态两种类型。静态故障主要在电机停止运行时发生,而动态故障则发生在电机运行过程中。动态故障的特殊性使其在实际使用中的检测难度较大。动态绕组匝间短路故障的检测难度大,主要是因为这种故障往往发生在电机的高速度、高负荷运行状态下,此时电机的电磁环境复杂,使故障信号容易被掩盖或混淆,从而增加了检测的难度。动态绕组匝间短路故障的检测效率低,主要是因为传统的检测方法在这种环境下效果不佳[4-7]。对于同步电机的短路故障检测,尤其是动态绕组匝间短路故障的检测,需要研发新的检测技术和方法,以提高检测的准确性和效率。
笔者通过改进的支持向量机(SVM)算法构建故障诊断模型,以提高动态绕组匝间短路故障的检测能力,满足同步电机运行要求。同时,采用灰色关联度分析和主成分分析提取故障特征,利用支持向量机(SVM)算法构建故障诊断模型,采用蚁狮算法(ALO)优化SVM的核函数参数和惩罚因子以提高其准确性和可靠性。
1 关键信号的特征提取
1.1 灰色关联度分析
灰色关联度分析是一种用于研究多个变量之间关联性和相互影响的方法。通过比较和分析不同因素在特定情境下的变化趋势和态势,来评估它们之间的关联程度。灰色关联度分析的基本思想是依据各个因素之间发展变化的一致性和存在的差异程度来判断它们的关系,从而决定各因素在系统中的地位。灰色关联度分析能够通过定量计算寻求因素间的主要关系,假设影响故障数据的参数是对比序列,Xi=(xi(1),xi(2),…,xi(n)),维度化后的n组样本的故障数据是参考序列,用Y=(y(1),y(2),…,y(n))表示,各个对比序列和参考序列相对应元素的相关系数为
(1)
式中:k——数据在序列中的位置,k=1, 2,…,n;
ρ——分辨系数,且0<ρ<1,通常取0.5。
通过式(1)计算相关系数ξi,分析故障数据和影响故障数据参数之间的关联性,挖掘比较序列和参考序列之间的信息得:
(2)
将式(2)计算的ri按照大小进行排序,ri越大,Xi对Y的影响就越大,确定对故障数据影响最大的一组参数。
1.2 主成分分析
主成分分析法是一种数据降维和特征提取的方法,它通过正交变换将原始数据中的冗余信息剔除,保留对结果影响较大的关键指标[8-9]。主成分分析法由数据预处理、协方差矩阵计算、特征值分解、选取主成分和数据转换构成。通过主成分分析法,可以将原始数据中的冗余信息剔除,同时保留对结果影响较大的关键指标。这有助于提高数据处理效率,降低数据冗余度,使数据分析更加精确和高效。
原始数据中对故障数据有显著影响的参数集合为
D=[dk(1),dk(2),…,dk(j)],
式中,j——故障参数维度。
协方差矩阵为
式中,D——标准化矩阵,其转置矩阵为DT。
计算协方差矩阵D的特征值矩阵S和特征向量矩阵为
R=V×S×V-1。
计算降维后的矩阵为
因此,故障参数之间的相关联系被打破,维度被降低,使SVM的预测精度提高。
2 XALO-SVM的故障诊断模型
在同步电机转子绕组匝间短路早期故障的诊断中,文中使用了一种改进的蚁狮算法(ALO)对支持向量机(SVM)算法进行优化。这种改进的方法旨在捕捉到转子绕组匝间短路故障的早期迹象,并提供更可靠和准确的诊断结果。通过采用改进的ALO算法优化SVM算法,能够更有效地处理和分析数据,进而提高故障诊断的准确性。
2.1 蚁狮算法的改进
蚁狮算法(ALO)是基于蚁狮如何构建漏斗状的蚂蚁陷阱来捕食蚂蚁的算法。ALO算法分为以下5个步骤。
步骤1初始化算法的相关参数,蚂蚁当前所在的坐标为
Xn,d=L+rand(U-L),
式中:Xn,d——当前所在的坐标,n=1,2,…,N,d=1,2,…,Dim;
Dim——参数维度;
N——初始种群数量;
U、L——蚁狮搜索蚂蚁的范围边界。
保存蚂蚁的坐标到Ma中,计算适应度值,获取当前蚂蚁在不同坐标下的适应度值,将适应度值进行保存。
比赛中,少先队员们个个精神昂扬,用充沛的感情和流畅的语言,博得了现场观众的阵阵掌声。而在其后的才艺展示环节中,跳舞、唱歌、乐器演奏,精彩不断……选手们用最大的热情展现出自己闪亮的风采。
步骤2轮盘赌在寻优算法中被广泛应用,轮盘赌可以随机选择一只合适的蚁狮,被选择的蚁狮随机行走,保存蚁狮行走的坐标,从Ma中抽取最佳方案,也就是精英蚁狮的位置,记录为Re。
X(t)=[c(2r(t1)-1),c(2r(t2)-1),…c(2r(tn)-1)],
(3)
式中:X(t)——蚂蚁所处坐标;
c——数据的累加结果;
t——当前迭代次数;
n——最大迭代次数。
随机函数r(t)的表达式,r在(0, 1)内随机、均匀地分布:
采用归一化处理,将蚂蚁游走范围限制在特定空间内,归一化式(3)为
ai——第i维变量随机移动步长的最小值;
bi——第i维变量随机移动步长的最大值;
cit——第i维变量第t代随机游走的最小值;
dit——第i维变量第t代随机游走的最大值。
(4)
(5)
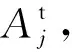
(6)
式中,I——随着迭代次数的增加而分段线性增加。
(7)
当前迭代次数为t,最大迭代次数为T,w取决于当前代数。
步骤3当蚂蚁分别围绕RA和RE游走时,均衡其产生的位置,并且更新蚂蚁的位置为

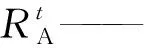
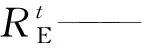
步骤4重新计算目标函数,将计算结果与之前的数据进行比较,以找出更好的值作为整体最优解。如果蚁狮的适应度值大于蚂蚁的适应度值,认为蚂蚁被蚁狮成功捕获,此时将更新蚁狮位置。通过将适应度值作为衡量标准,蚁狮的位置不断更新,以寻找更优的解决方案。
步骤5在算法中,需要添加一个判断是否等于最大迭代次数的条件。如果等于了最大迭代次数,则输出当前已获得的全局最优解。否则,继续执行步骤2到5,持续进行优化。
通过在蚁狮算法中引入自适应边界,使蚂蚁在蚁狮附近游走时有更多的选择。通过引入自适应边界,蚁狮算法的搜索空间将更加丰富,从而有助于找到更好的解决方案。这种方法的数学表达式为
(8)
由式(7)可知,边界的变化与I值成反比,在式(8)中的I值由10w、t/T、(0.5+sin(tπ/2Trand))这三个因子决定。随着迭代次数增加,10w呈线性分段指数递增,t/T呈线性递增,(0.5+sin(tπ/2Trand))在0.5到1.5内呈非线性的递增。由于I值的变化趋势为非线性,则I值具有更多的变化情况,增加了蚂蚁在游走过程中的随机概率,从而提高了算法整体寻找最优解的能力,可以更容易获取最优解。
第一种情况:在蚂蚁在蚁狮的陷阱范围非常接近时,距离因素起着相当大的作用。由于两者的距离非常相近,蚂蚁易被蚁狮捕捉,也更容易被当前最优的蚁狮所吸引。因此,如果采用类似于俄罗斯轮盘赌的随机游走策略,可能会选择距离最近的解作为最优解来进行随机游走。在这种随机游走过程中,蚂蚁最终的随机游走位置将被更新为(9)。α、β、γ是三个参数,它们的和等于1,默认情况下设置为0.33。在实际应用中,根据具体情况适当调整这些参数值。
(9)
第二种情况:当蚂蚁与任何蚁狮的陷阱范围距离较远时,距离因素不再起作用。在此种情况下,蚂蚁的最终随机游走位置保持不变。
(10)
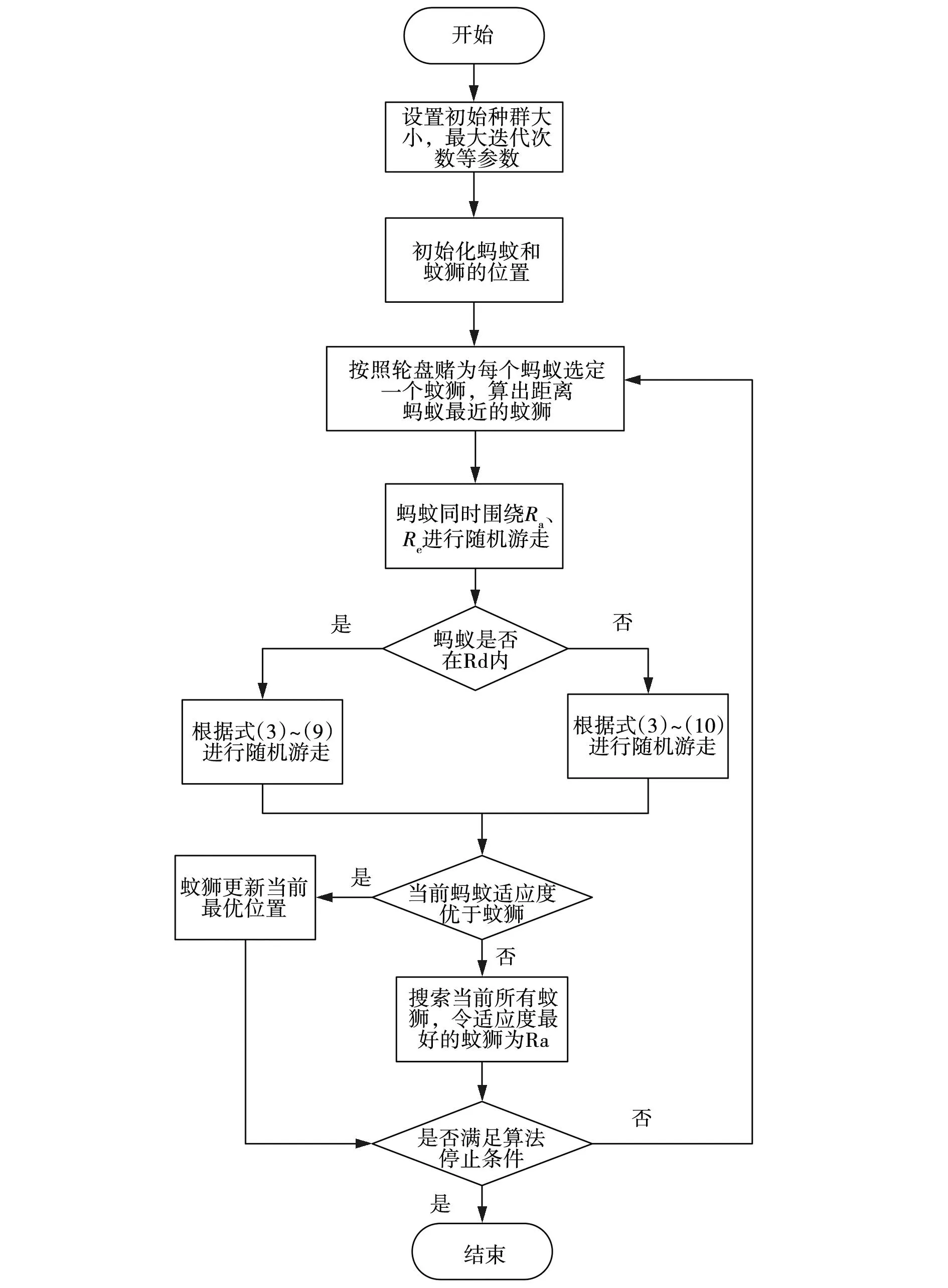
由于ALO算法的目的是利用适应度轮盘赌选择随机的蚁狮,这一点通过在原始蚁狮算法中按大小排序[13],然后设置,如果A XALO-SVM算法流程如图1所示。由图1可见,通过设定一些参数,包括初始种群大小、最大迭代次数、适应度函数的维度、变量的上下限等。这些参数将用于算法的运行和优化过程[10-11]。初始化处理的步骤包括设定每个蚁狮和蚂蚁的起始位置。这些位置是随机确定的,可以根据问题的特点进行适当的选择。随后,计算每个蚁狮和蚂蚁个体的适应度,并根据计算出的适应度的大小对每一个蚁狮和蚂蚁个体进行排序。这样,就可以得到一个初始种群,其中个体按适应度从高到低排列。因此,随着迭代次数的增加,适应度较高的蚁狮将具有更高的捕食概率,被视为精英蚁狮RD。使用轮盘赌算法为每个蚂蚁选择一个蚁狮,记为RE。同时,计算蚂蚁与RE之间的距离,找到距离蚂蚁最近的蚁狮,记为RD。根据式(4)~(6)进行判定,如果蚁狮在RD的捕食范围内,蚂蚁根据式(9)进行游走。其中,参数I根据式(13)进行调整。否则,蚂蚁根据式(10)进行游走,并更新蚂蚁的位置。在每次迭代中,如果当前蚂蚁的适应度高于蚁狮RE或RD,就会用当前蚂蚁的位置替换掉RE或RD的位置,并重新对蚂蚁进行随机的初始化,以便进行下一轮迭代。对所有蚁狮按照适应度大小排序,标记最大适应度的蚁狮为RA。当算法达到所设定的最大迭代次数或最优结果时,将此条件设为终止条件,此时输出RA作为最优结果。否则,返回步骤3,开始进行下一次迭代。 图1 XALO-SVM算法流程Fig. 1 XALO-SVM algorithm flow 基于改进的蚁狮算法,构建了支持向量机故障诊断模型,主要目的是通过优化支持向量机的核函数参数来提高诊断模型的准确度。考虑到蚁狮算法的优势,将改进的蚁狮算法与支持向量机算法相结合,以提高故障诊断模型的稳定性和准确性。基于XALO-SVM的异常模式识别分为9个步骤。 步骤1设置诊断模型的各项参数,包括惩罚因子C和核函数的取值范围。 步骤2对ALO算法的边界和轮盘赌按照2.2的方法进行优化。 步骤3初始化种群。根据惩罚因子C和核函数的取值范围确定蚁狮算法初始种群变化区间,形成初始化种群。 步骤4计算适应度函数值。将SVM故障识别模型准确率作为蚁狮算法适应度函数,计算不同的故障识别模型准确率,选择本次计算最高的适应度值对应精英蚁狮。 步骤5更新蚂蚁和蚁狮的位置。 步骤6根据适应度函数来计算蚁狮和蚂蚁的适应度值,通过适应度值来重新分配精英蚁狮的位置。 步骤7查看当前迭代次数是否已经是最大的迭代次数,如果符合上述的终止条件,则执行步骤8操作;如果不满足,则继续执行上述的步骤5至步骤7。 步骤8通过上述计算获取支持向量机算法的最佳参数。 步骤9根据获得的SVM最佳性能参数,基于测试数据进行模型验证,判断所寻找的最优参数是否满足精度要求。 图2 XALO-SVM的故障识别技术路线Fig. 2 Roadmap of fault Identification technology for XALO-SVM 实验验证基于改进蚁狮算法的支持向量机故障诊断模型,实验采用同步电机故障模拟机组,其额定转速为1 000 r/min,额定容量为30 kV·A,额定电压为400 V,功率因数为0.8,相数为3,隐极转子虚槽数为42,实槽数为30,如图3所示。将同步电机转子绕组匝间短路故障的分为3类,总共有2 700个原始的数据样本,三种类型的样本数量分别为900个。通过实验验证,评估基于改进蚁狮算法的支持向量机故障诊断模型在该同步电机故障模拟机组上的性能。实验结果的目的是验证该模型在诊断同步电机转子绕组匝间短路故障方面的准确性和可靠性。通过实验评估该模型在不同情况下的表现,以确定其是否能够有效地诊断该故障。 图3 实验装置Fig. 3 Experimental setup 通过对同步电机转子绕组匝间短路的分析,影响故障诊断过程的参数包括功率因数A1、径向气隙A2、定子内径A3、定子槽数A4、转子槽数A5、极对数A6、定子铁芯长度A7、同步电抗A8、额定励磁电流A9和额定容量A10。每个参数之间具有相关性,通过第1节的灰色关联度分析和主成分分析对参数进行分析处理。将影响故障诊断结果的10个参数作为比较序列Xi=(xi(1),xi(2),…,xi(700)),其中,i=1, 2,…, 10,把同步电机转子绕组匝间短路故障类型作为参考序列Y=(y(1),y(2),…,y(700)),采集同步电机转子绕组匝间短路过程中的数据,利用灰色关联度分析处理原始数据,结果如表1所示。 表1 不同变换方法的装配质量灰关联度 通过灰色关联度计算,将影响故障结果的10个参数进行排序,选取其中影响最大的参数A1、A3、A4、A5和A6,从而获取关键故障参数。此外,为了消除上述选定参数之间的相互关联性,通过主成分分析法对选定的参数进行优化,消除参数间的关联性保证数据层面的准确性。选定参数的累积贡献率和累积贡献率如表2所示。 表2 装配参数特征值及累积贡献率 为了检验所提出的方法在故障诊断问题上的可行性和实用性,并与其他算法模型进行比较,进行了以下实验设计和分析。首先,选择PSO-BP、SVM、PSO-SVM和LSTM算法作为比较对象。为了保证实验的有效性和公平性,设置了相同的种群数目20和迭代次数最大值100。对这五种算法模型进行了10次运行,不同算法模型在故障诊断问题上的性能指标变化趋势,如图4所示。 图4 各算法模型准确率对比Fig. 4 Comparison of accuracy of various algorithm models 由图4可以看出,文中所提出的方法在某些方面相较于其他算法具有明显的优势。同时,将这些结果整理在表3中,以便进行更具体的数值比较。通过对比不同算法模型的性能指标,可以发现本文所提出的方法在某些情况下表现出了更好的性能和优越性。综上所述,通过实验设计和结果的分析,全面评估了所提出方法的优越性。从定量和定性的角度进行论述,文中提出的算法在故障诊断问题上表现出更好的性能和优越性,进一步验证了该方法的有效性和可行性。因此,文中所提出的方法在故障诊断问题上具有明显的优势和良好的应用前景。 表3 各算法模型平均准确率 从图4和表3可以看出,所采用的XALO-SVM算法在准确性方面表现最佳,其准确率与其他算法相比具有明显优势。同时,文中所提出的XALO-SVM算法在运行时间上相比PSO-SVM算法降低了15%,进一步证实了该算法的优越性。研究中比较了子群算法、最初始的ALO算法和上述改进更新后的ALO算法的有效性。尽管PSO算法的收敛速度较快,但容易过早收敛,从而降低了寻优深度。相比之下,原始ALO算法和改进后的ALO算法虽然收敛速度较慢,但在寻优结果方面表现更为优越。特别是在迭代次数足够大时,改进后的ALO算法明显优于原始ALO算法。 (1)通过灰色关联度分析和主成分分析法对原始数据集进行处理,降低数据集的复杂性。这两种方法能够有效地提取数据集中的特征信息,确保所提取的特征信息能够充分反映出原始数据集中的关联性。特征信息的提取降低数据维度,减轻算法的计算负担,同时确保不损失关键信息。这有助于建立更加高效和精确的故障诊断模型。 (2)采用XALO-SVM算法构建故障诊断模型,结合了灰色关联度分析和主成分分析法的优势,提高了计算的稳定性和准确性。基于XALO-SVM的故障诊断模型诊断精度可达97%以上,同时也缩短了诊断时间,为故障检测提供了技术支持。2.2 XALO-SVM的故障识别流程
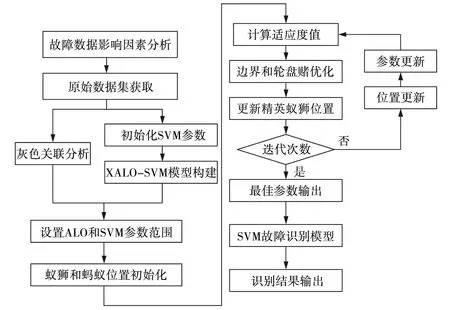
3 实例验证

3.1 关键信号特征提取
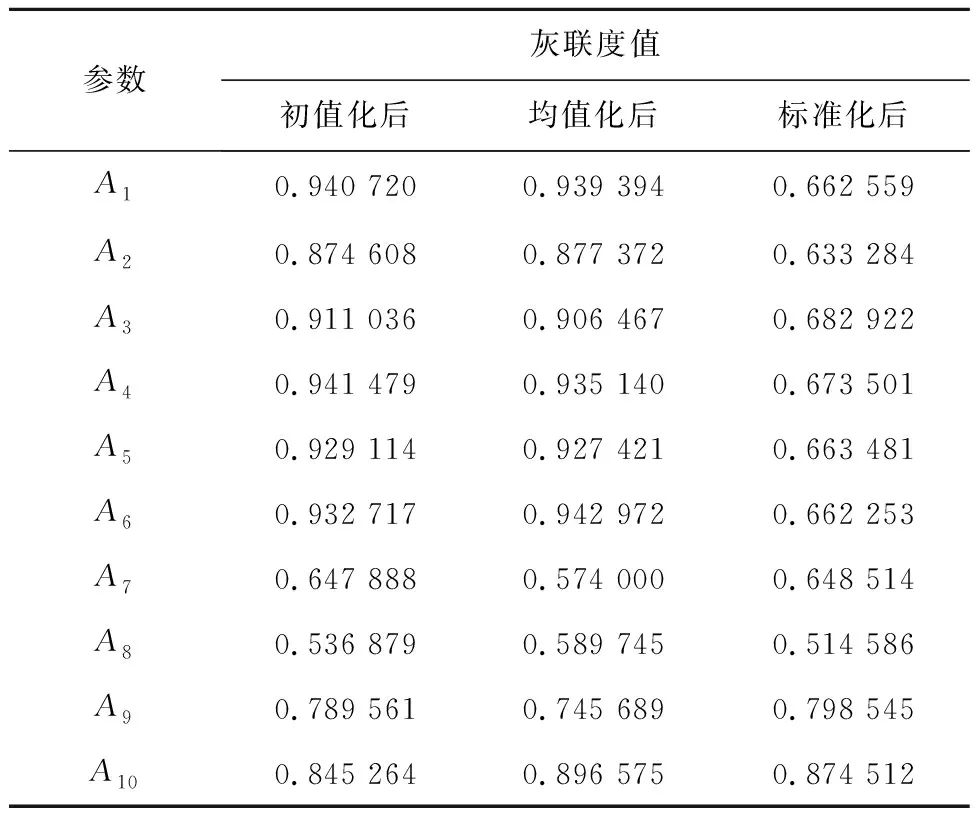

3.2 基于XALO-SVM的故障诊断
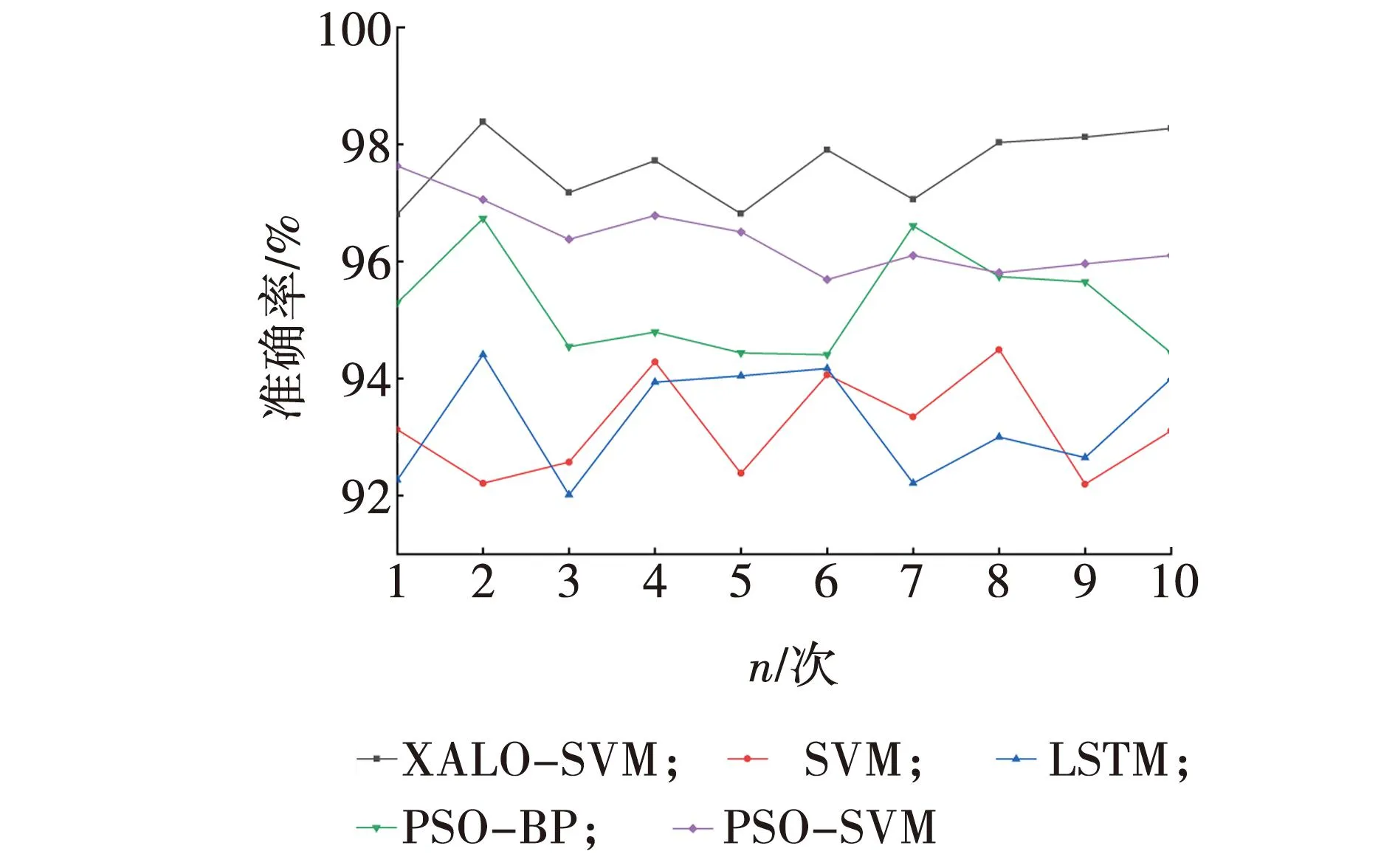

4 结 论
