改进模糊滑模的永磁同步电机控制

赵 杰, 王富利, 张 瑞

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

能源是发展的前提,目前我国火力发电量占总发电量的80%,对煤矿资源依赖巨大。为适应经济发展的需要,煤矿的采掘效率要进一步提升。随着电力电子技术和电气传动技术的发展,永磁驱动技术已经在多个领域得到了应用,在矿山采掘中也有着广阔的发展前景。矿山环境复杂,因此矿用永磁同步电机对抗干扰性有着更高的要求。传统的PI控制已经很难满足实际的需要,学者们利用非线性控制的方法设计了很多方案[1-2],SMC因为具有很强的鲁棒性[3-4],实现方法简单而被广泛关注。

SMC控制存在超调量大、响应时间慢和抖振过大的问题。为解决这些问题,大量学者做了研究。王湘明等[5]引入系统状态变量来改进传统指数趋近律,构建了新的滑模控制器,在电机启动阶段有效减小了转速超调量,但当负载突变时,抑制超调量的效果不理想。苗敬利等[6]提出一种幂次指数趋近律和模糊自适应相结合的方法,有效抑制了超调量,减小了转速误差,但收敛时间相较传统SMC有所增加。徐冬磊[7]利用模糊控制优化了指数函数的等速趋近项系数,有效抑制了抖振现象,但在抑制超调量和提高响应速度方面存在不足。沈维等[8]改进了传统的积分滑模面,并用边界层可变的饱和函数代替不连续的开关函数,削减了抖振的程度,减小了稳态误差。王红艳等[9]在指数趋近律的基础上引入加权积分型增益,抖振得到了削减,受到扰动时误差更小,但仍然存在超调量。

笔者在以上研究的基础上,采用一种自适应的指数趋近律,以此构建的滑模控制器(ISMC)有效减弱超调量,提高系统反应速度,但抗干扰性较SMC提升不大,故引入模糊控制将改进后的指数趋近律进行优化,优化后滑模控制器(FISMC)有着更好的控制性能,有效地提高了电机的运动品质。

1 PMSM数学模型

表贴式PMSM基于旋转坐标系下的数学模型为

(1)

式中:TL——负载转矩;

J——转动惯量;

Φf——永磁体磁链。

式(1)经过坐标变换,得到静止坐标系下的电压方程为

(2)

定义系统状态变量为

(3)

根据式(2)与式(3),可以得:

(4)

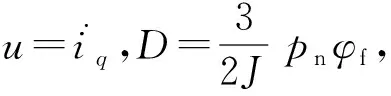
(5)

2 滑模控制器的构造

2.1 SMC

定义滑模面函数为

s=cx1+x2。

(6)

对式(6)求导,可得:

(7)

一般指数趋近律表达式为

(8)

采用指数趋近律方法,联立式(5)(7)(8),可得控制器的表达式为

(9)

根据式(9)和(5),从而可得q轴参考电流为

(10)

定义Lyapunov函数为

(11)

对式(11)求导得:

(12)

将式(8)代入式(12)可得:

(13)

故满足可达条件。

2.2 IMSMC

指数趋近律的系数对系统的超调,抖振和反应时间影响很大,因此,设计一种随系统状态变化而变化的新趋近律可以有效地改善运动品质。

在指数趋近律的基础上,提出自适应指数趋近律为

(14)

(15)

在指数趋近律的基础上增加了|x1|f(ω)项,其中:|x1|为系统状态量,ωm为实际转速,ωref为给定转速,引入系统状态量|x1|,可以使指数趋近律的等速趋近项的系数随系统状态变化而自适应变化 ,同时为了进一步提高趋近律的收敛速度和精确速度,用ωref/ωm进一步修正|x1|的值。在速度误差较大时,以|x1|>1为例,因ωref/ωm>1,故ε|x1|ωref/ωm>ε,即距离滑模面较远时,改进的趋近律有着更快的收敛速度;当|x1|<1时,因ωref/ωm>1,故ε|x1|ωref/ωm<ε,即在距离滑模面较近时,改进的趋近律有着更小的趋近速度,可以减少抖振的发生。因在传统指数趋近律中引入了系统自身状态量,故可以达到自适应调节的目的。

联立式(5)(7)(14)(15)可得,控制律为

(16)

将式(14)(15)代入式(12)中得:

-ε|s||x1|f(ω)-qs2<0。

(17)

满足可达性条件,证明用改进的趋近律搭建的控制器是稳定的。

2.3 模糊控制

根据图5和6可知,IMSMC消除了SMC在空载中出现的超调量,并减少了到达参考转速的时间,但是突加负载时SMC跟IMSMC的最大速度误差的差值仅为3 rad/min,且突加负载时SMC跟IMSMC转矩响应能力基本相同,可见IMSMC动态运动性能较SMC改善不大,为了进一步提高IMSMC的控制性能,提高抗干扰能力,引入模糊控制对IMSMC进一步优化。模糊控制可以优化指数趋近律的系数,从而进一步提高系统的运动品质。在IMSMC的基础上,选取s和ds作为模糊控制器的输入,输出△ε和△q作为系数ε和q的修正量,构建模糊滑模控制器(FIMSMC)。

整定模糊规则时按照下面的原则:远离滑模面时,适当增大q的取值,以提高系统的趋近速度;靠近滑模面时,适当增大ε,以保证运动品质量。

输入输出对应的模糊集为{NB,NM,NS,ZO,PS,PM,PB}。设计模糊规则如表1和2所示。

表1 参数△ε模糊控制规则

采用Mamdani模糊算法并用重心法解模糊,隶属度函数如图1所示。△q和△ε的3D调整,如图2所示。

图1 隶属度函数Fig. 1 Membership function

图2 △q的自调整3D网格Fig. 2 Self-adjusting 3D grid of △q

系统的超调量,调节时间和稳态误差是相互影响的,单纯调节系统的某一个参数不能实现既削减超调量又提高趋近速度的目的,因此引入模糊控制,根据系统状态同步调节参数q和参数ε。

在离滑模面较远时,此时ε对系统影响是有限的,参数q是影响趋近速度的主要原因。此时由图2可知,在系统离滑模面较远,且运动趋势为远离滑模面时,此时赋予△q较大的数值,以加快趋近到滑模面的速度;在系统处于趋近过程但是离滑模面较近时,此时给予△q一般大的数值,这样有利于减缓运动的惯性。

在离滑模面较近时,如图3所示。适当增大△ε的值以保证运动的品质,同时赋予△q较小的值,以削减q对系统抖振的影响。

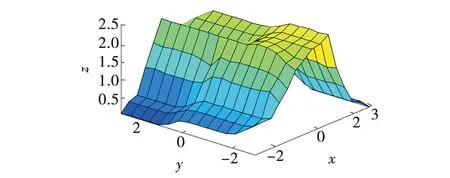
图3 △ε的自调整网格Fig. 3 Self-adjusting grid for △ε

3 仿真验证

通过Simulink进行搭建模型并仿真,选用表贴式永磁同步电机,id=0的控制方式,仿真时间为0.4 s。PMSM参考转速为1 400 rad/min,当0.2 s时给电机突加15 N的负载,初始转矩常量设置为1.05 N·m。仿真整体框图如图4所示。

电机仿真参数:定子电阻设定为2.875 Ω,极对数为4,电感为8.5×10-3H,转动惯量为0.003 kg·m2,磁链为0.175 WB,黏滞阻尼为0.008 N·m·s。

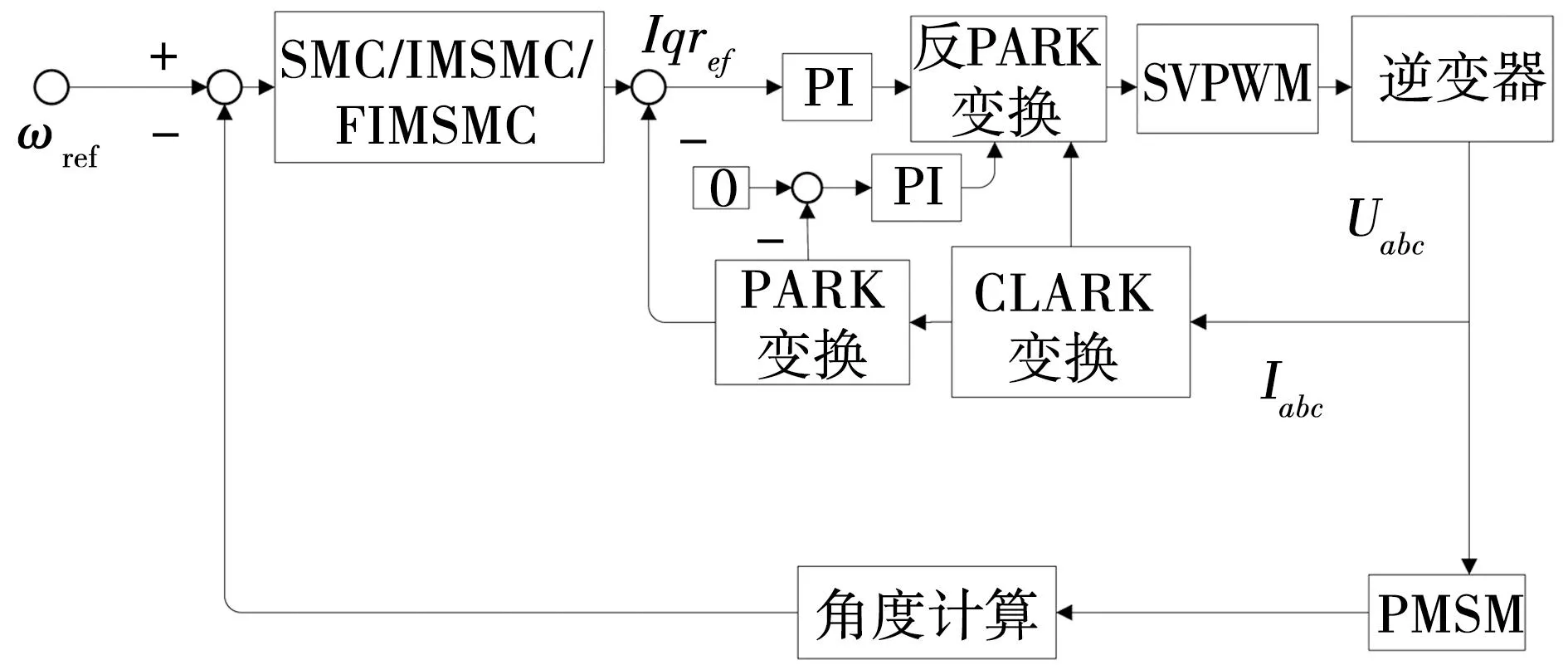
图4 仿真整体模型Fig. 4 Simulates overall model

3.1 SMC和IMSMC仿真对比

仿真结果如图5～8所示。由图5b可知,空载启动时SMC存在着很大的超调量,而IMSMC可以实现无超调量启动,且空载初始启动阶段SMC到达参考转速的时间较长,IMSMC到达参考转速的时间很短。由图6b可知,空载启动时IMSMC有着更好的转矩响应特性,相比SMC来说 ,IMSMC转矩误差波动更小且能更快地到达初始参考转矩。

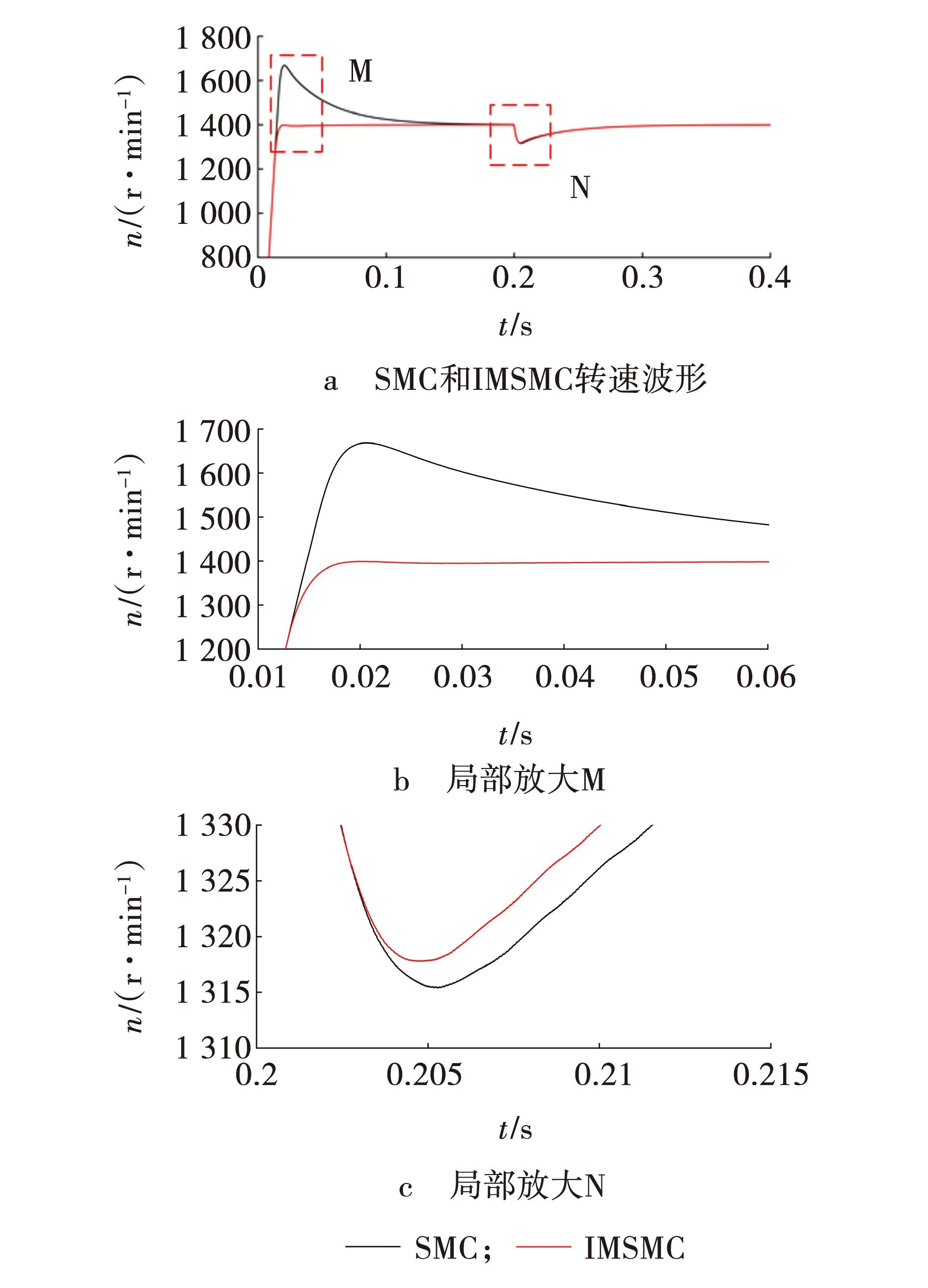
图5 空载与突加负载下的转速对比Fig. 5 Comparison of rotational speeds under no-load and sudden load

由图5c可知,突加转矩后,IMSMC的转速最大误差更小,恢复至参考转速的时间更短,但相较SMC来说,IMSMC对转速误差的提升是有限的。由图6c可知,突加转矩后,SMC和IMSMC在同一时间到达参考转矩,说明IMSMC对SMC在突加转矩上对转矩响应上的提升基本无效果。

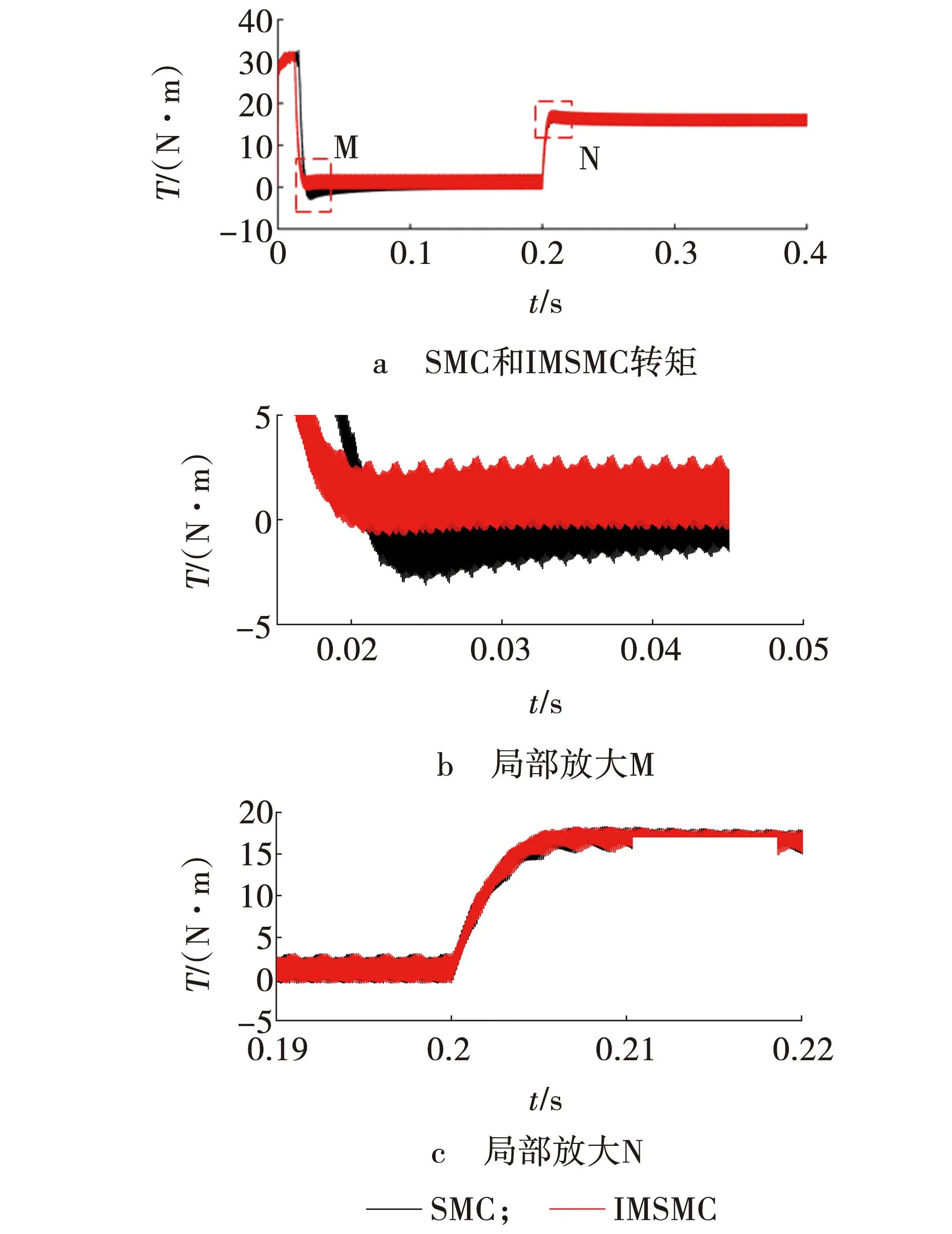
图6 空载与突加负载下的转矩对比Fig. 6 Comparison of torque at no load and sudden load

由图7b可知,空载时,FIMSMC在IMSMC的基础上,进一步减少了到达参考转速的时间,且同IMSMC一样,可以实现无超调量启动。由图8b可知,初始空载阶段,相较 IMSMC来说,FIMSMC进一步缩短了到达参考转矩的时间。

由图7和8c可知,突加负载时,FIMSMC的转速最大误差较IMSMC有着明显减小,且恢复至参考转速的时间更短;突加负载时,FIMSMC能更快地到达参考转矩,有着更好的转矩响应能力,比IMSMC的抗干扰能力更强。

SMC/IMSMC/FIMSMC三种控制策略具体的转速跟踪数据如下:空载启动时FIMSMC要比SMC快0.13 s到达参考转速,且无超调量;加负载时,FIMSMC要比SMC快0.1 s恢复至原速度,且误差更小。在空载状态下,SMC控制算法下超调量为19.16%,到达额定转速时间为0.2 s,IMSMC和FIMSMC可以无超调量启动,且到达给定转速时间分别为0.08和0.12 s。

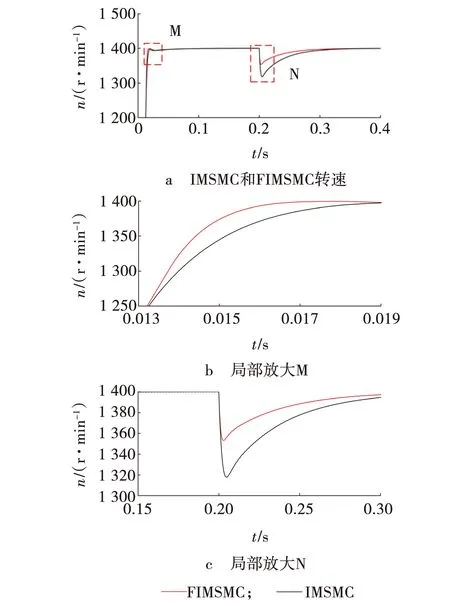
图7 空载与突加负载下的转速对比Fig. 7 Comparison of rotational speeds under no-load and sudden load

图8 空载与突加负载下的转矩对比Fig. 8 Comparison of torques at no load and sudden load

3.2 IMSMC和FISMC仿真对比

突加负载状态下,SMC控制算法下恢复至参考转速的时间是0.2 s,最大转速误差为6.04%,IMSMC和FIMSMC恢复至参考转速的时间分别为0.18和0.12 s,最大转速误差分别为5.87%和3.34%。

空载启动时FIMSMC要比SMC快0.13 s到达参考转速,且无超调量;加负载时,FIMSMC要比SMC快0.1 s恢复至原速度,且误差更小。

4 结 论

(1)针对SMC存在的超调量大、调节时间慢、抗干扰性差的问题,在SMC基础上,改进了一种IMSMC,通过模糊算法将IMSMC进一步优化得到FIMSMC,仿真实验验证了文中提出的FIMSMC算法可以极大减小控制误差,改善PMSM控制的动态性能。

(2)IMSMC控制算法实现了空载时对PMSM调速的无超调启动,较SMC有着更快的调节时间,但在突加负载仿真中,IMSMC提升较SMC不明显,故引入模糊控制算法,将ISMC进一步优化提出FISMC。仿真结果证明:空载启动时,FISMC到达参考转速的时间较SMC减少 0.13 s;突加负载时,FISMC较SMC减小2.7%的最大误差,证明了FISMC有着更好的控制性能。