基于剪力比的自复位支撑结构体系主体框架设计
2024-03-11孟丽岩潘雨桐刘吉胜
王 涛, 孔 涛, 孟丽岩, 潘雨桐, 刘吉胜
(黑龙江科技大学 建筑工程学院, 哈尔滨 150022)
0 引 言
自复位防屈曲支撑(Self-centering buckling-restrained brace,SCBRB)由防屈曲支撑和自复位系统组成[1],在小震下,支撑不进入屈服,与主体框架共同抵抗地震作用,能够有效地控制结构变形;在大震作用下,支撑耗能内芯发生拉伸或压缩,能稳定耗散地震能量,复位系统帮助结构实现复位,能够减小结构的残余变形,增强结构的可恢复性[2]。
现有研究已证明SCBRB在结构的消能减震领域具有优良的性能[3-4],但目前SCBRB在建筑结构中应用相对较少,其原因是针对自复位支撑结构体系的设计方法还不完善,对该结构体系的抗震设计还存在着较大的争议,主要集中在设计时如何调整各抗侧力体系的水平抗剪能力,以实现多重设防的抗震目标,即存在匹配性问题[5-6]。为了解决匹配性问题,诸多学者从不同角度开展了研究,刘建彬[7]对低层的BRB钢框架进行弹塑性时程分析,给出了低层防屈曲支撑钢框架抗侧刚度比建议取值为3.0~5.0。赵瑛等[8]引入支撑与框架的抗侧刚度比作为主要控制参数,给出了抗侧刚度比的合理取值范围及相应抗侧刚度比下允许设计的最弱框架。潘毅等[9]通过引入支撑与整体结构的剪力比作为主要控制参数,给出了剪力比的合理取值范围,并给出了相应剪力比下允许设计的最弱框架。
匹配性问题涉及两个抗侧力体系,即支撑体系和框架体系,其中,框架体系对整体结构的抗震性能起关键作用,若主体框架太强,则会影响支撑的耗能;若主体框架太弱,则支撑屈服后,主体框架没有足够的刚度抵抗侧向力,使得整体结构极易发生破坏。因此,为解决自复位支撑结构体系中存在的匹配性问题,必须对主体框架进行合理的初步设计。
笔者提出了一种基于剪力比的自复位支撑结构体系主体框架初步设计方法,首先,将剪力比与基于位移的设计方法相结合,并介绍了SCBRB基于位移的抗震设计流程;然后,根据不同的复位比λ和剪力比α设计了多组不同参数的自复位支撑钢框架,在8度大震下对结构模型进行弹塑性时程分析,得出α的合理取值范围;最后,在α的合理取值范围的基础上,结合不同刚度的主体框架再次设计多组不同参数的自复位支撑钢框架,对结构模型进行8度小震下的反应谱分析和8度大震下的弹塑性时程分析,给出相应剪力比下主体钢框架弹性层间位移角限值的建议取值。
1 SCBRB的参数设计
剪力比α定义为支撑承担的地震剪力Fs与结构总剪力Fy的比值,即:
α=Fs/Fy。
由此可见,只需确定结构总剪力和剪力比,就能得到支撑承担的地震剪力。文中采用基于位移的抗震设计方法[10-11]对SCBRB进行设计,设计流程如下。
本次设计选择第三水准,查表1确定结构在设计水准下的目标层间位移角。

表1 SCBRB钢框架结构性能指标
计算结构等效阻尼比ξeq。
μb=θd/θby,
θby=δby/(hcosβ),
δby=σyl/E,
λ1=λ+r(1+λ)(μb-1),
式中:μb——支撑的延性系数;
θd——结构在设计水准下的目标层间位移角;
θby——支撑达到轴向屈服时的结构层间位移角;
δby——支撑的轴向屈服变形;
β——支撑与水平方向的夹角;
σy——支撑金属耗能内芯的屈服强度;
l——支撑长度;
E——弹性模量;
h——层高;
ξv——初始黏滞阻尼比,钢结构取0.02;
Rξ——与耗能系统采用的材料相关的参数,采用金属耗能时,Rξ取0.557;
λ——复位比,即复位系统预应力与耗能系统屈服力的比值,为保证支撑有足够的复位能力,λ常取大于1的常数;
r——支撑第二刚度与第一刚度的比值,可取0.05。
通过式(1)~(4)将自复位防屈曲支撑结构等效为单自由度(Single degree of freedom, SDOF)结构,结构侧移形状选择直线型。
Δi=Hiθd,
(1)
(2)
(3)
(4)
式中:Δd——SDOF结构的等效位移;
mi——第i层的楼层质量;
Δi——第i层在设计水准下的目标位移;
me——SDOF结构的等效质量;
He——SDOF结构的等效高度;
Hi——第i层楼层距底面高度。
设计位移反应谱可由设计加速度反应谱通过式(5)、(6)转换得到。
Δd(T,5%)=Sa(T,5%)T2/(4π2),
(5)
(6)
式中:Sa(T,5%)——5%阻尼的设计加速度反应谱;
T——结构周期。
计算各楼层设计剪力Fi、支撑承载力需求Fs和支撑变形需求δs。
Keff=me4π2/Teff2,
Fd=KeffΔd,
Fs=αFi/(nicosβ),
δs=Δtcosβ,
式中:Keff——SDOF结构等效刚度;
Teff——SDOF结构等效周期;
Fd——SDOF结构基底剪力;
Fi——楼层设计地震作用力;
n——楼层数;
ni——第i层设置的支撑数;
Δt——设计层间位移。
根据Fs和δs,确定SCBRB的相关设计参数。
A=F0/σy,
p0=λF0,
k1=(1+λ)F0/δby,
k2=rk1,
δu>δs,
式中:A——支撑的耗能内芯的截面面积;
F0——耗能系统的屈服力;
p0——复位系统的预应力;
k1——第一刚度;
k2——第二刚度;
δu——支撑的极限变形。
2 有限元模型建立及地震动选取
2.1 结构设计
为了研究复位比对剪力比取值的影响规律并得到剪力比的合理取值范围,本节根据4种不同的复位比0、0.4、0.8、1.2和7种不同的剪力比0.1、0.2、0.3、0.4、0.5、0.6、0.7,采用基于位移的设计方法设计了多组SCBRB钢框架结构。结构所处设防等级为8度(0.2 g),场地类别为II类,设计地震分组为第二组,楼面恒、活荷载标准值分别取6、2.5 kN/m2。
研究对象包含3种不同层数结构,3种层数结构的总层高分别为11.7、19.5、35.1 m,每层层高均为3.9 m,图1为结构布置示意。

图1 结构布置示意Fig. 1 Schematic of structural layout
框架梁、柱采用Q345钢,SCBRB耗能内芯材料采用Q235钢。梁采用I型截面,柱采用箱型截面,当结构层数为3层时,梁截面尺寸为235 mm×235 mm×6 mm×12 mm,柱截面尺寸为270 mm×270 mm×10 mm×10 mm;当结构为5层时,梁截面尺寸为265 mm×265 mm×8 mm×14 mm,柱截面尺寸为300 mm×300 mm×10 mm×10 mm;当结构为9层时,梁截面尺寸为250 mm×250 mm×6 mm×12 mm,1~5层柱截面尺寸为450 mm×450 mm×12 mm×12 mm,6~9层柱截面尺寸为400 mm×400 mm×14 mm×14 mm。
2.2 数值模型
采用ABAQUS进行结构反应谱分析和弹塑性时程分析,支撑简化方式和支撑-框架结构建模方法参考文献[12]。钢材弹性模量E为206 GPa,强化系数为Et=0.01E,泊松比υ为0.3。框架梁柱采用梁单元B31简化模拟,钢材的材料模型采用Chaboche模型。自复位防屈曲支撑分解为耗能系统和复位系统两部分,耗能系统采用桁架单元T3D2简化模拟,复位系统采用非线性弹簧简化模拟,最后通过耗能系统与复位系统并联对整个SCBRB进行简化模拟。
2.3 地震动选取
根据规范[13]要求,弹塑性时程分析选用了8条地震波,相关参数如表2所示。其中,sp为地震动峰值加速度,t为地震波持续时间。天然地震波选自PEER地震波数据库,人工波根据场地条件合成,分析时将所有地震波的sp调整到4 m/s2。图2为加速度反应谱,图中sa表示谱加速度。
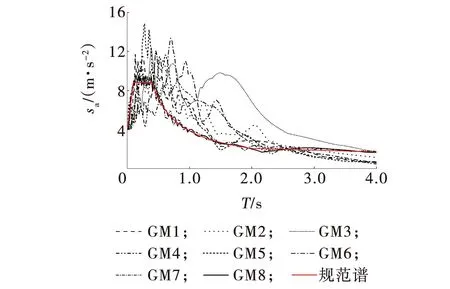
图2 加速度反应谱Fig. 2 Acceleration response spectra
由图2可知,对于周期小于2.5 s的短周期和中长周期结构,6条天然地震记录的反应谱能够覆盖规范反应谱的临近区域,结构弹塑性时程分析的结果能够较好地反映结构在大震下的性能[14]。
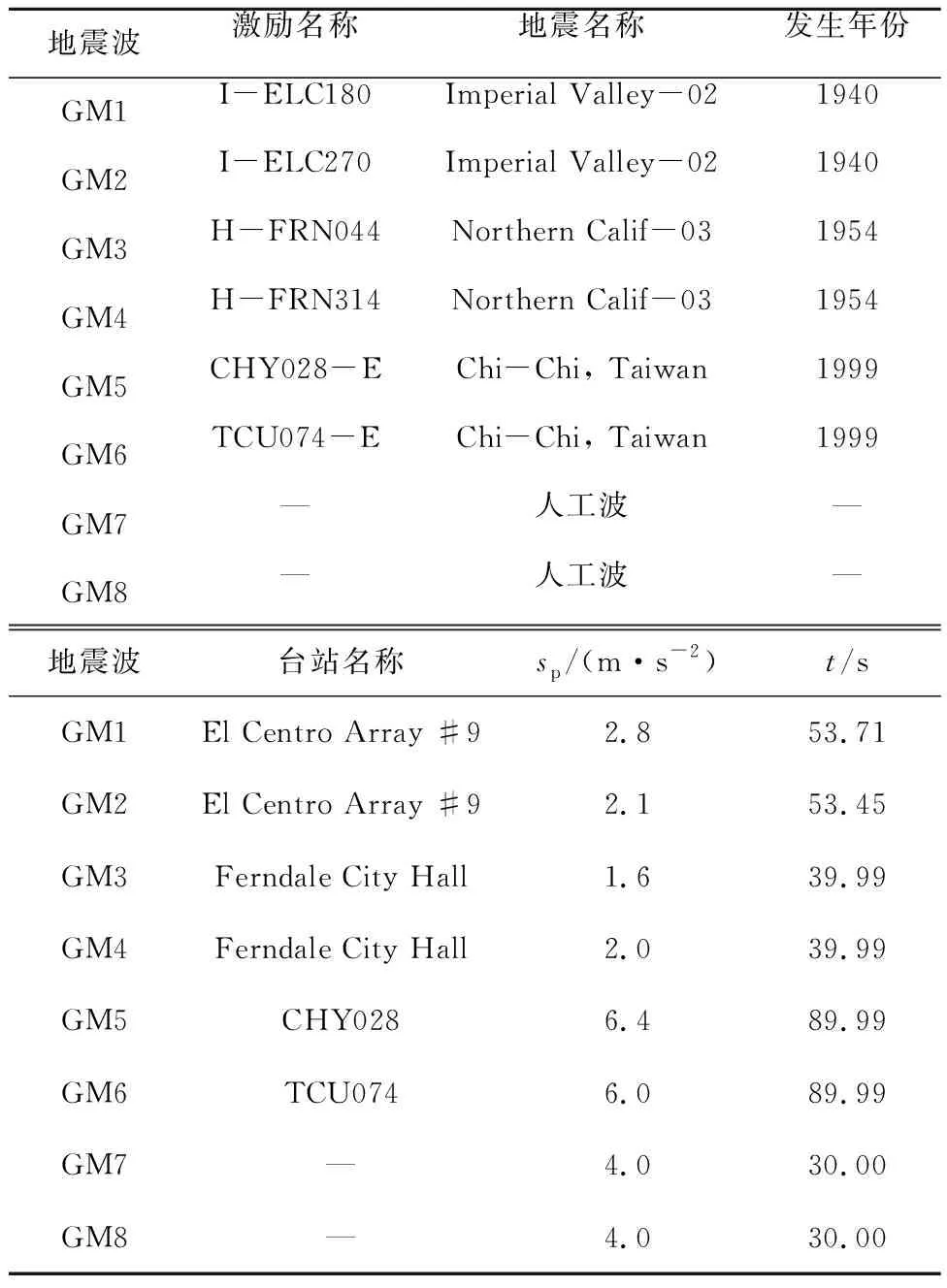
表2 地震波详细信息
3 剪力比的合理取值范围

图随α的变化关系Fig. 3 Relationship between and α

图随α的变化关系Fig. 4 Relationship between and α

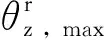
图5 3种层数结构随α变化规律对比Fig. 5 Comparison of variation of three kinds of layer structure with α
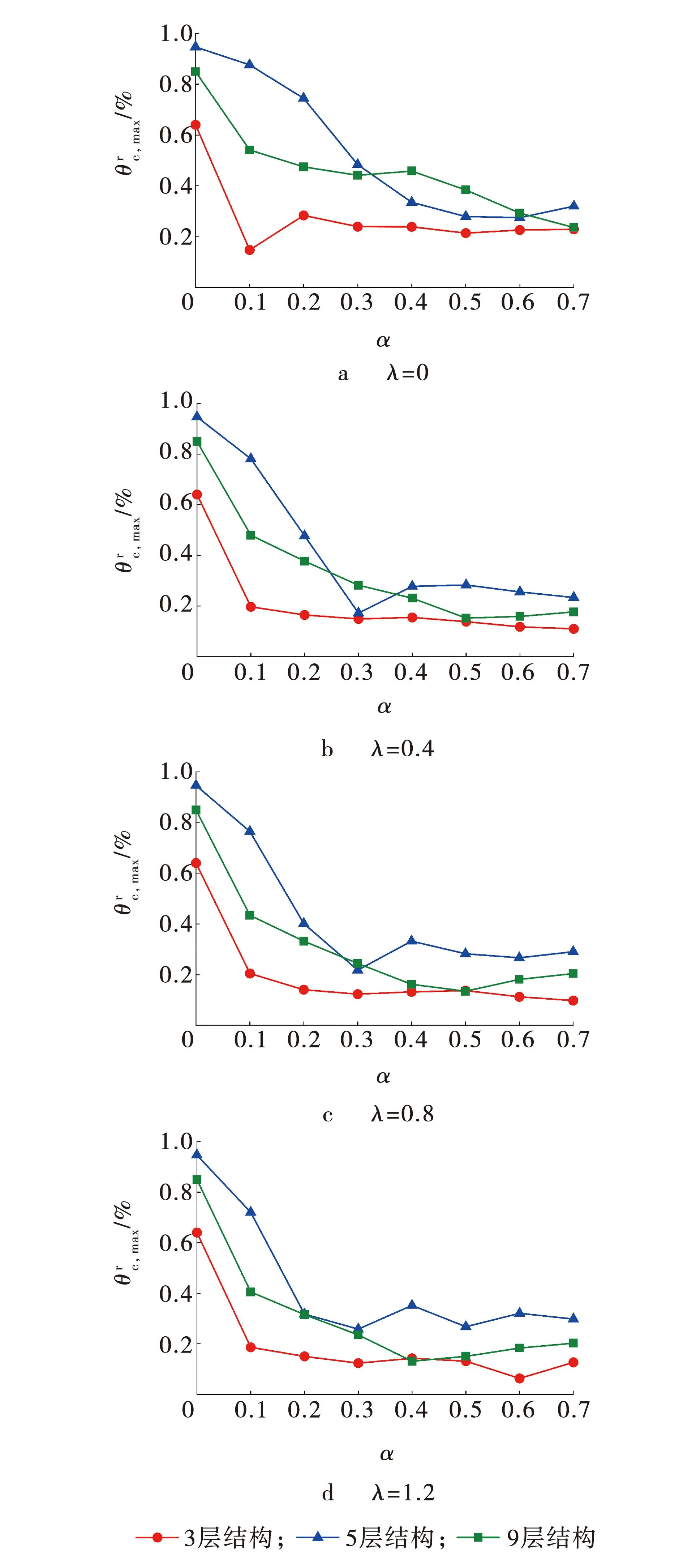
图6 3种层数结构随α变化规律对比Fig. 6 Comparison of variation of three kinds of layer structure α
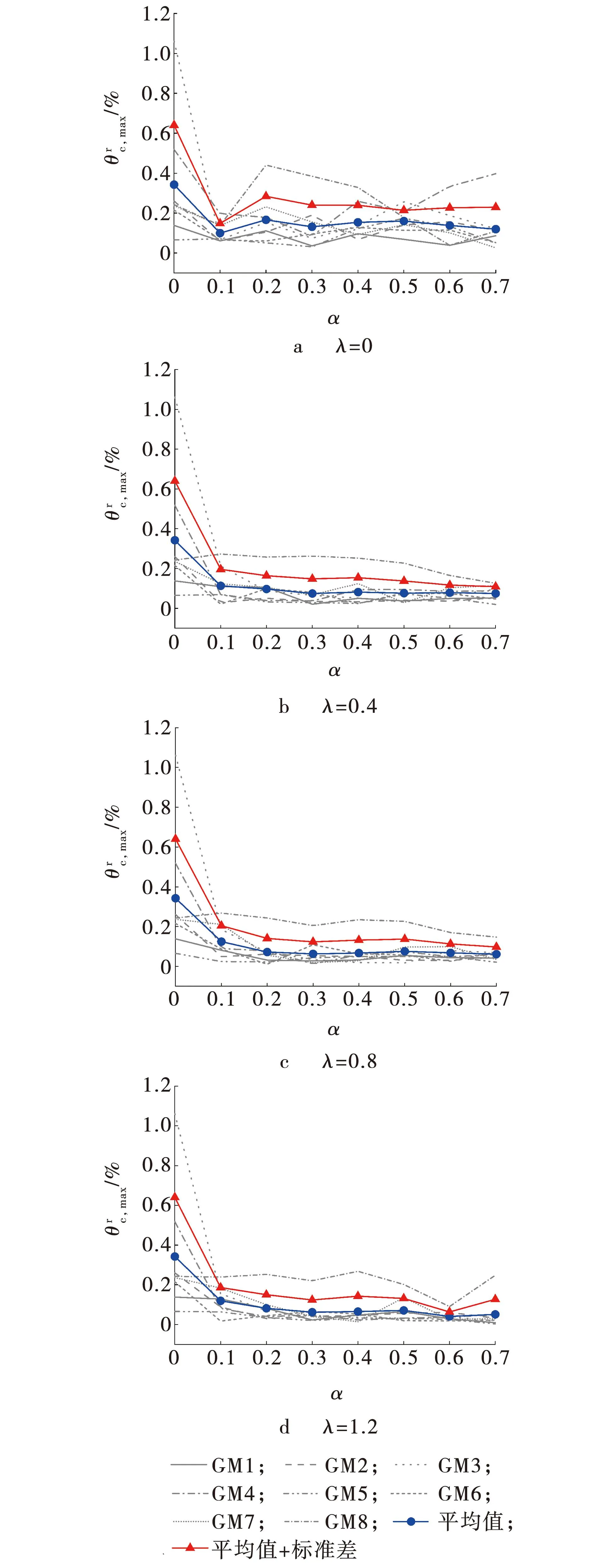
综合考虑,对两个指标(最大层间位移角和最大残余层间位移角)的分析结果取交集,在进行结构设计时,建议SCBRB钢框架结构中剪力比α的合理取值范围为0.3~0.5。
4 主体框架初步设计建议值
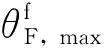
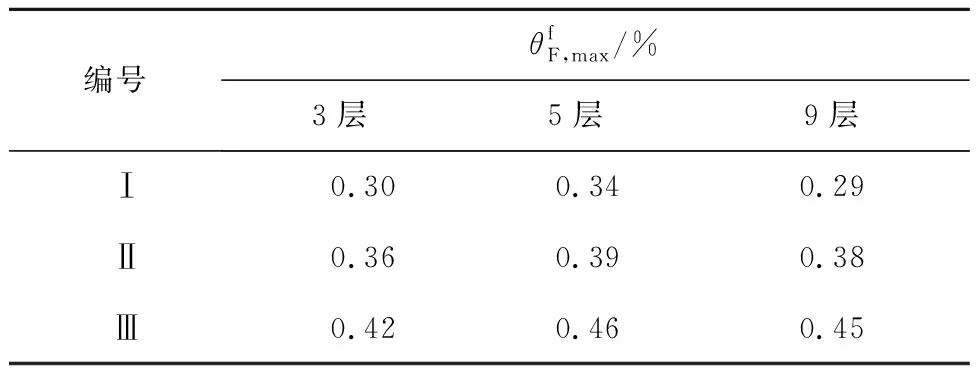
表3 不同刚度主体钢框架小震下最大层间位移角
由图7可知,随着主体框架刚度逐渐减小,整体结构的地震响应也逐渐增大,整体来看,本节选取的所有空框架在设置自复位防屈曲支撑后,结构在小震下最大层间位移角均能满足规范[13]中弹性层间位移角限值的要求,表明自复位防屈曲支撑在小震下能为结构提供足够的附加刚度,能够有效控制结构变形。
然后,对上述27个结构模型进行8度大震下的弹塑性时程分析,所选用的地震波与2.3节相同,同样采用各地震波计算值的平均值与标准差之和作为参考值,分析结果如图8所示。
由图8a可知,随着主体框架刚度逐渐减小,3层、5层和9层结构的大震下的位移响应均呈现出增大的趋势。其中,3层和5层结构中主体框架刚度最小的结构模型在大震下的最大层间位移角大于1/50,此现象表明,当主体框架刚度过小时,整体结构无法满足大震下的性能要求。
由图8b和8c可知,三种层数的所有空框架分别按照α为0.4和0.5设置自复位防屈曲支撑后,结构模型在大震下的最大层间位移角均小于1/50,表明结构的实际抗震性能满足预期的设计要求。
根据图7和图8的分析结果,综合考虑:
按照支撑设计剪力比0.3设置SCBRB时,主体框架弹性层间位移角限值的建议取值为[θ]=1/263。
按照支撑设计剪力比0.4设置SCBRB时,主体框架弹性层间位移角限值的建议取值为[θ]=1/238。
按照支撑设计剪力比0.5设置SCBRB时,主体框架弹性层间位移角限值的建议取值为[θ]=1/217。
5 结 论
(1)根据结构最大层间位移角和最大残余层间位移角随剪力比的变化规律,并考虑复位比对取值的影响规律,给出SCBRB设计剪力比的合理取值范围为0.3~0.5。
(2)在剪力比的合理取值范围的基础上,进一步研究了主体框架与剪力比的匹配性,当剪力比为0.3、0.4、0.5时,主体钢框架弹性层间位移角限值的建议取值分别为1/263、1/238、1/217。
