TBM豆砾石回填灌浆层性能与密实度对支护效果的影响

杨风威　金俊超　杨凡杰

关键词：双护盾ＴＢＭ；隧洞施工；豆砾石回填灌浆；管片衬砌；灌浆层密实度；支护效果

中图分类号：ＴＶ５４３ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２４．０１．０２４

引用格式：杨风威，金俊超，杨凡杰．ＴＢＭ 豆砾石回填灌浆层性能与密实度对支护效果的影响［Ｊ］．人民黄河，２０２４，４６（１）：１３９－１４５．

我国经济目前处于迈向高质量发展的新阶段，一批长距离引调水工程、公路铁路隧道、城市地铁等基础设施相继开工建设。由于掘进速度快、隧道成型好、对围岩扰动小以及作业安全等优点，ＴＢＭ（Ｔｕｎｎｅｌ ＢｏｒｉｎｇＭａｃｈｉｎｅ）被越来越多地运用于隧洞施工中［１－２］ 。在双护盾ＴＢＭ 施工过程中，通常采用预制衬砌管片、回填豆砾石和灌浆的方式进行支护。围岩与衬砌管片之间空隙先进行豆砾石回填，其后通过灌浆处理，使围岩、回填层与衬砌管片形成整体支护结构承担荷载，同时使回填豆砾石灌浆层形成封闭防渗圈，提高隧洞防渗性能［３］ 。

豆砾石回填灌浆是ＴＢＭ 隧洞施工的重要环节，直接影响整体衬砌质量以及工程长期正常运行安全［４］ 。然而，由于现场影响因素众多，施工难度大，常会遇到豆砾石回填灌浆层性能与密实度达不到设计要求的问题［５－８］ 。近年来，国内外研究人员在豆砾石回填灌浆体施工质量控制及影响因素方面进行了大量研究［９－１６］ ，如：罗志鑫［１３］ 结合实际ＴＢＭ 豆砾石回填灌浆质量检验情况，提出了豆砾石回填灌浆体的检验标准；杨建明［１４］ 结合达坂隧洞的工程概况及地质情况，对该隧洞灌浆中存在的串浆不规律、原材料质量不稳定、后配套灌浆平台压力大等问题进行了分析，并提出了一些解决方法。但是，豆砾石回填灌浆层性能与密实度缺陷会对衬砌结构造成什么影响，是否有必要采取工程处理措施，仍缺少深入系统的研究。

本文以西北某双护盾ＴＢＭ 施工的引水隧洞为工程依托，从现场选取回填灌浆层芯样，进行单轴压缩试验，分析不同区域回填豆砾石灌浆体的弹性模量及强度变化。在此基础上，借助数值模拟手段，建立管片衬砌的梁－弹簧模型，从管片受力及变形的角度，分析多种工况下豆砾石回填灌浆层性能与密实度的影响因素。

１ 工程概况

西北某输水隧洞全长３１．２６ ｋｍ，为有压隧洞，内水压力最大为１．２ ＭＰａ，常规运行期内水压力为０．７ＭＰａ。其中，ＴＢＭ 洞段长约２４．４ ｋｍ，采用２ 台直径为５．４８ ｍ 的双护盾ＴＢＭ 施工，相向掘进。输水隧洞Ⅱ类围岩段总长度约为１４．８３ ｋｍ，Ⅲ类围岩段总长度约为９．９５ ｋｍ，Ⅳ类围岩段总长度为５．５９ ｋｍ，Ⅴ类围岩基本为断层、总长度约为０．８９ ｋｍ。

ＴＢＭ 开挖断面为圆形，开挖直徑为５．４８ ｍ，采用预制装配式钢筋混凝土管片衬砌，管片内径４．６ ｍ、外径５．２ ｍ、厚度３０ ｃｍ。在掘进过程中，盾体与围岩间隙为２５～５０ ｍｍ，管片与围岩间隙理论值为１４ ｍｍ，隧洞开挖后围岩与管片间的空隙采用豆砾石充填并进行灌浆。

２ 室内试验分析

为研究豆砾石缺陷体的物理力学性质，从ＴＢＭ 开挖洞段不同部位钻取豆砾石灌浆体岩芯，加工成高径比为２ ∶ １ 的标准试样，共３８ 个。每个试件的加工精度（包括平行度、平直度和垂直度）均控制在《水电水利工程岩石试验规程》（ＤＬ／ Ｔ ５３６８—２００７）规定的范围之内。

豆砾石灌浆体典型岩样如图１ 所示，由于豆砾石灌浆体的灌浆密实度不同，岩样表面的蜂窝现象也不相同，密实度越差，岩样表面的蜂窝现象越严重。图中红色物质为树脂材料，用于填补岩样端面的坑槽，防止因端面坑槽的存在而导致岩样受压过程出现偏心。

单轴压缩试验在多功能岩石试验机上进行：加载阶段采用轴向力控制，轴向变形采用两个高精度差动式位移传感器（ＬＶＤＴ）进行测量，侧向变形采用两个粘贴在梁式弹簧片上的全桥电路进行测量。

由图２ 可见，不同部位豆砾石灌浆体的单轴抗压强度差异较大。在３８ 个豆砾石灌浆体试样中，单轴抗压强度＜１０ ＭＰａ 的试样比例为６３．１６％，１０ ＭＰａ≤单轴抗压强度＜１５ ＭＰａ 的试样比例为２１．０５％，单轴抗压强度≥１５ ＭＰａ 的试样比例为１５．７９％。豆砾石灌浆体单轴抗压强度按照钻孔部位进行分类时，规律性不明显，原因可能是取样时钻孔主要位于每环管片的下半部。

此外，受钻孔条件的限制，隧洞顶部区域未能实现取芯，而实际隧洞顶部的灌浆效果要偏差些。

不同部位豆砾石灌浆体的变形模量差别也较大，分析豆砾石灌浆体的单轴抗压强度与变形模量的试验结果，二者之间存在一定的正相关性（见图３）。

试验后豆砾石灌浆体岩样典型破坏情况如图４ 所示，不同部位豆砾石灌浆体试样的破坏类型均为沿最大主应力方向的劈裂破坏，即试样破坏时多条裂缝沿轴向发展，同时，试样破坏时，其环向呈现不同程度的鼓胀现象。

３ 豆砾石回填灌浆层性能对支护效果的影响

３．１ 计算模型

采用圆形框架结构模拟隧洞衬砌， 以梁单元ＢＥＡＭ１８８ 模拟混凝土管片衬砌， 以弹簧单元ＣＯＭＢＩＮ１４ 模拟隧洞轴向混凝土对模型的约束作用，以点－点接触单元ＣＯＮＴＡＣ５２ 模拟衬砌外围岩体、喷层混凝土和回填豆砾石对管片衬砌的约束作用，以弹簧单元ＣＯＭＢＩＮ３９ 模拟相邻管片间的相互作用。圆形框架的半径为衬砌混凝土中心线至隧洞轴线的距离２．４５ ｍ，梁单元厚度为衬砌厚度０．３ ｍ，梁单元宽度方向为隧洞轴向，宽度取单环管片长度１．５ ｍ。

最大轴力发生在２２ 号梁单元上，位于衬砌的顶部管片Ｄ 的中部，拉力为０．３６０ ０ ＭＮ；最小轴力发生在５８ 号

梁－弹簧模型在笛卡儿直角坐标系中建立，坐标原点位于圆形框架结构的圆心，整体坐标系的Ｚ 轴沿隧洞轴线方向，指向上游为正，Ｙ 轴沿铅直方向，铅直向上为正，Ｘ 轴以右手法则确定。为便于表述，将各节管片依次编号为Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ（见图５）。

３．２ 计算条件及方案

针对Ⅳ类围岩内外水头差为７５ ｍ 的情况，假定衬砌管片外围与豆砾石均接触良好，不存在脱空部位。根据室内试验成果，确定豆砾石回填灌浆层的力学参数，进行敏感性分析，结果见表１、表２。

３．３ 方案ＸＮ１ 结果分析

鉴于不同方案计算结果相近，以方案ＸＮ１ 为例，进行计算结果分析。如图６ 所示，在结构自重和内水压力的作用下，管片衬砌的轴力均为正值，数值为０．０５９ ０～０．３６０ ４ ＭＮ，说明衬砌结构为整体受拉状态。最大轴力发生在２２ 号梁单元上，位于衬砌的顶部管片Ｄ 的中部，拉力为０．３６０ ０ ＭＮ；最小轴力发生在５８ 号梁单元上，位于底部管片Ａ 的两个接缝附近，拉力为０．０５９ ０ ＭＮ。

管片衬砌的弯矩可近似认为关于Ｙ 轴对称分布，弯矩为－０．０２２ ９～０．０１２ ７ ＭＮ·ｍ，最大弯矩发生在５６号梁单元上，位于管片Ｂ 靠近管片Ａ 的接缝位置；最小弯矩发生在７０ 号单元上，位于衬砌的底部管片Ａ中部位置。

管片衬砌的剪力为－０．０４９ １～０．０５４ ８ ＭＮ，最大剪力发生在５９ 号梁单元上，位于管片Ａ 和管片Ｂ 的接缝附近；最小剪力发生在８２ 号单元上，位于管片Ａ 和管片Ｆ 的接缝附近。

对于梁－弹簧模型，根据内力分布特征，从图６ 可以看出管片各个断面以受拉为主，整理分析各个截面位置的拉应力包络线，按下式求取衬砌环向最大拉应力：

式中：σ_ｍａｘ为所求点的环向最大拉应力；Ｍ 为由梁－弹簧模型求得该点的弯矩；Ｎ 为由梁－弹簧模型求得该点的轴力；ｙ 为该点距中性轴的距离，对于管片内侧或外侧是出现拉应力最大值的可能位置，即ｒ ＝ ２．３ ｍ 或ｒ ＝２．６ ｍ 处，ｙ ＝ ±０．１５ ｍ；Ｉ 为衬砌截面对中性轴的惯性矩；Ａ 为衬砌截面面积。

将最大拉应力乘以荷载分项系数１．２，混凝土抗拉强度除以安全系数１．２，为强度允许值，比较两者大小得到混凝土强度（拉应力）包络线校核结果。从图７可以看出，在环向角度为１８０°（底部管片Ａ 中部）附近最大拉应力已经超过强度允许值，具体位置在环向角度为１６２° ～ １９３°处，说明在此处不能满足强度校核要求。

３．４ 不同方案结果分析

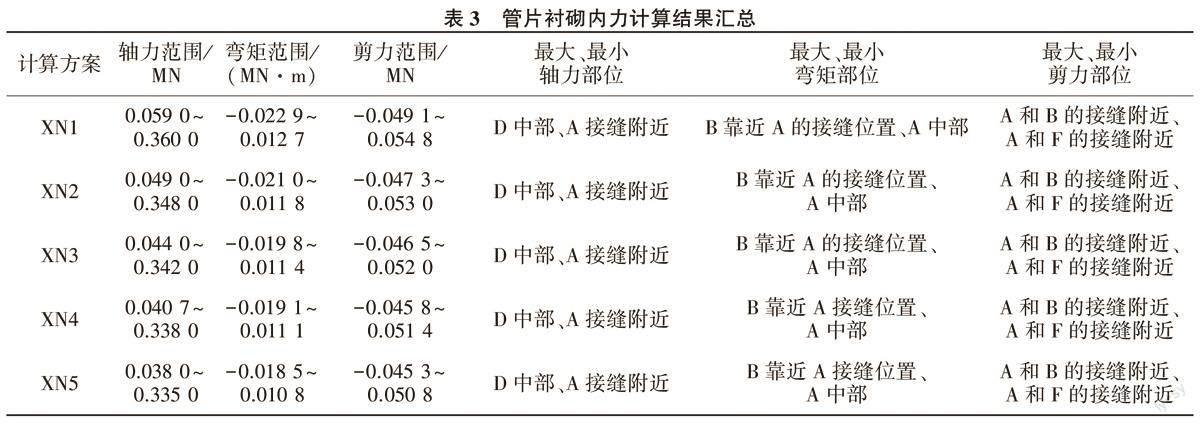
将不同方案计算结果进行整理汇总，见表３。在衬砌与豆砾石不存在脱空状态的条件下，豆砾石参数取值不同对衬砌的受力分布并不产生影响，最大、最小轴力部位，最大、最小弯矩部位，最大、最小剪力部位都没有出现明显的变化，主要差异在于衬砌各个部位的应力有所变化，因此豆砾石参数取值会对衬砌各个部位的应力产生影响。在整体规律上，管片衬砌的轴力始终为正值，衬砌整体受拉，轴力随着豆砾石变形模量增大而逐步减小；弯矩和剪力有正有负，内力大小变化幅度不大。

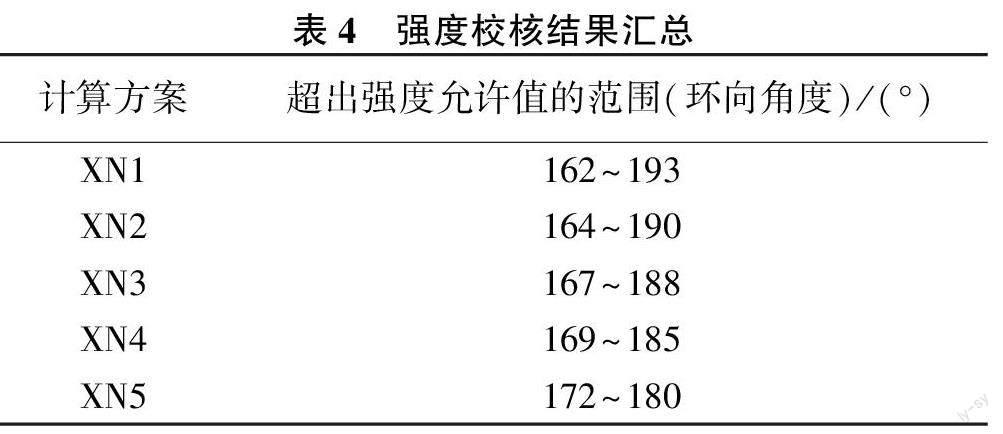
由表４ 可知，在衬砌与豆砾石不存在脱空状态和豆砾石参数取值不同的情况下，衬砌强度校核结果所体现的规律基本一致，管片Ａ 中部（环向１８０°）拉应力超出混凝土强度允许值，其余部位拉应力均未超出混凝土强度允许值。随着豆砾石变形模量的增大，超出强度校核要求的范围逐渐减小，由３１°（１９３°～１６２°）左右下降到８°（１８０°～１７２°）左右。

同时，考虑到梁弹簧单元计算模型，在底管片得到的应力大于实体单元模型的，因此综合各种因素可以估算：在豆砾石变形模量增大的过程中，应力的超限范围逐渐减小，但是由于豆砾石本身厚度较薄，其力学参数对管片结构安全的影响并不是很突出，对于豆砾石变形模量不小于３．０ ＧＰａ 的情况，管片衬砌应不会出现二次开裂，衬砌结构安全性较好。

４ 豆砾石回填灌浆层密实度对支护效果影响分析

综上所述，豆砾石与衬砌不存在脱空现象的情况下管片结构应力分布以及应力数值相差不大，但在脱空情况下有待进一步研究。不考虑豆砾石材料性能的影响，变形模量采用设计参数３．０ ＧＰａ，计算模型及其他参数与上述保持一致。

４．１ 计算方案

受地质条件、施工工艺以及材料特性等多种因素的影响，豆砾石回填灌浆缺陷的类型、分布及其范围具有一定的随机性。综合已建工程资料，主要缺陷类型分布大致遵循如下规律：１）管片顶部位置易形成空洞或纯水泥结石体；２）在管片侧上部易形成灌浆不密实体；３）在管片侧下部易形成纯水泥芯样；４）高岩粉缺陷最易发生在管片底部。

上述不同类型缺陷均可能导致管片脱空，为了全面反映不同情况，根据豆砾石回填灌浆层质量缺陷出现位置，将衬砌分为底部管片Ａ、顶部管片Ｄ、腰部下方管片Ｂ 和腰部上方管片Ｃ 四个典型管片，针对各典型管片，考虑到豆砾石回填灌浆层质量缺陷出现在管片端部和管片中部位置的不同（环向约６０ ｃｍ 范围），共拟定８ 个计算方案（见表５），各方案脱空示意见图８。

４．２ 方案ＹＸＴＫ０１结果分析

鑒于不同方案计算结果相近，以方案ＹＸＴＫ０１ 为例，进行计算结果分析。由图９ 可知，在结构自重和内水压力的作用下，管片衬砌的轴力均为正值，数值为０．０８８ ６～０．５２４ ３ ＭＮ，说明衬砌结构为整体受拉状态。最大轴力发生在６４ 号梁单元上，位于衬砌底部管片Ａ豆砾石脱空部位的端部，拉力值为０．５２４ ３ ＭＮ；最小轴力发生在９６ 号梁单元上，位于管片Ｅ 与管片Ｆ 的接缝位置，拉力值为０．０８８ ６ ＭＮ。

管片衬砌的弯矩可近似认为关于Ｙ 轴对称分布，弯矩值为－０．０６８ ７～０．１６５ ６ ＭＮ·ｍ，最大弯矩发生在７１ 号梁单元上，位于底部管片Ａ 豆砾石脱空部位的中部，说明豆砾石脱空使得该部位衬砌出现较明显的受弯现象；最小弯矩发生在６０ 号梁单元上，位于衬砌底部管片Ａ 的支撑脚位置。

管片衬砌的剪力值为－０．４２０ ０～０．４１６ ８ ＭＮ，最大剪力发生在７７ 号梁单元上，位于底部管片Ａ 豆砾石脱空部位的右端，最小剪力发生在６４ 号单元上，位于衬砌底部管片Ａ 豆砾石脱空部位的左端。

从管片梁－弹簧模型的内力分布情况来看，与豆砾石不脱空情况相比，管片内力出现明显变化，内力的最值多出现在脱空部位，需要引起注意。

梁－弹簧模型的混凝土强度和抗裂包络线（拉应力）如图１０ 所示，在环向角度为１８０°（底部管片Ａ 中部）附近最大拉应力已经超过强度允许值，具体范围为环向角度１３０°～２２６°，该区域主要为豆砾石脱空部位，说明在此处衬砌混凝土不能满足强度校核要求。同时，图１０（ｂ）中的环向应力有超过混凝土标准抗拉强度的区域，该区域主要集中在豆砾石脱空部位，说明在此计算条件下，该区域管片可能开裂。

４．３ 不同方案计算结果分析

将不同方案计算结果进行整理汇总，见表６。各方案在豆砾石脱空位置中部出现最大环向拉应力，且均已超过强度允许值，衬砌混凝土不能满足强度校核要求的区域主要集中在豆砾石脱空部位，同时各方案在底部管片Ａ 的中部附近均已超出混凝土强度要求，因此对于豆砾石脱空各部位以及底部管片Ａ 的中部位置需要引起注意。

５ 结论

１）从隧洞不同部位取３８ 个豆砾石灌浆充填体试样，进行单轴压缩试验，发现不同部位豆砾石灌浆体的单轴抗压强度和变形模量差异显著，而泊松比变化相对较小，整体上豆砾石灌浆体单轴抗压强度与变形模量存在正相关关系。

２）在衬砌与豆砾石不脱空的情况下，豆砾石参数取值不同对衬砌受力分布并不产生影响，但衬砌各部位应力会有所变化。整体规律上，管片衬砌轴力始终为正值，衬砌整体受拉，轴力随豆砾石变形模量增大而逐步减小；弯矩和剪力有正有负，内力大小变化幅度不大。衬砌强度校核结果规律基本一致，均表现为环向１８０°处拉应力超出混凝土强度允许值，随着豆砾石变形模量的增大，超出强度校核要求的范围逐渐减小。

３）在不考虑豆砾石回填灌浆层性能影响的情况下，衬砌与豆砾石脱空部位受力状态与不脱空时产生明显差异，脱空部位管片出现了较为明显的受力现象，部分区域的应力甚至超过了衬砌混凝土抗拉强度設计值，可能出现裂缝。脱空部位衬砌混凝土不能满足强度校核要求，同时底部管片中部附近也超出了混凝土强度要求。

４）本文分别分析了豆砾石回填灌浆层性能和密实度对支护效果的影响，但实际工程地质条件、施工过程较为复杂，可能出现二者不利状况的耦合。在隧洞施工中应当重点关注衬砌与豆砾石之间是否紧密结合，加强豆砾石回填、灌浆的质量监督。

【责任编辑 简群】