基于CEEMDAN-GMDH-ARIMA的大坝变形预测模型研究

程小龙　张斌　刘相杰等

关键词：自适应噪声完备集成经验模态分解；数据处理群集法；差分自回归移动平均模型算法；大坝；变形预测；江西上犹江水电站

中图分类号：ＴＶ６９８．１＋ １ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２４．０１．０２５

引用格式：程小龙，张斌，刘相杰，等．基于ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 的大坝变形预测模型研究［Ｊ］．人民黄河，２０２４，４６（１）：１４６－１５０．

随着我国水利工程技术的快速发展，大坝数量不断增加，其作为我国重要的水利工程设施，具有建筑规模大、运行时间久等特点，在各种不确定因素的影响下，易产生变形［１］ 。准确预测大坝变形趋势有利于维护大坝安全，保持大坝稳定运行［２］ 。大坝发生变形是由水位、水压、温度和时效等多种因素导致的，各影响因素内在联系复杂，主次关系难以确定［３］ ，很难做出准确可靠的大坝变形预测。目前，大坝变形预测常用方法包括回归分析法、时间序列法、支持向量机、神经网络等［４］ 。这些方法各具特点，但也存在一些弊端，难以充分挖掘大坝变形数据的复杂性和非线性特征，预测精度较低。因此，越来越多的学者将数据处理方法引入大坝变形数据分析，并与神经网络模型进行组合来改善预测效果。例如：周兰庭等［５］ 针对变形数据序列的非线性、非平稳性等特點，提出基于ＣＥＥＭＤＡＮＰＳＲ（相空间重构）－ＫＥＬＭ（核极限学习机）的大坝变形预测模型。鄢涛等［６］ 采用集合经验模态分解（ＥＥＭＤ）和极限学习机（ＥＬＭ）实现了大坝变形预测。董泳等［７］ 采用ＥＥＭＤ 对经验模态分解（ＥＭＤ）后的高频分量继续分解，实现有效变形信息的挖掘，提高了预测精度。但上述研究大都是针对非线性特征建模，忽略了大坝变形数据中的周期性和趋势性特征分析。因此，集成线性分析预测模型与非线性分析预测模型，对大坝变形预测分析具有重要意义。

神经网络具有良好的自适应性、自组织性、自学能力以及联想、容错、抗干扰能力，可以全面反映各因素的非线性特征，考虑各种因素对大坝变形的影响。与ＢＰ 神经网络、ＲＢＦ 神经网络等一般神经网络相比，ＧＭＤＨ 神经网络能够专门针对复杂非线性系统进行自组织建模，对于高阶非线性系统的辨识更加有效［８－９］ ，目前已被广泛应用于经济、工程、军事等领域［１０－１２］ 。ＡＲＩＭＡ 是一种用于时间序列分析预测的模型，能够捕捉数据中的线性关系，常用于处理分析线性信号［１３］ 。

针对大坝变形数据的复杂性和非线性等特征，本文建立ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 模型，并将该模型应用到江西上犹江水电站大坝变形预测，以验证该模型的合理性和可行性。

１ 基本原理与方法

１．１ ＣＥＥＭＤＡＮ 算法

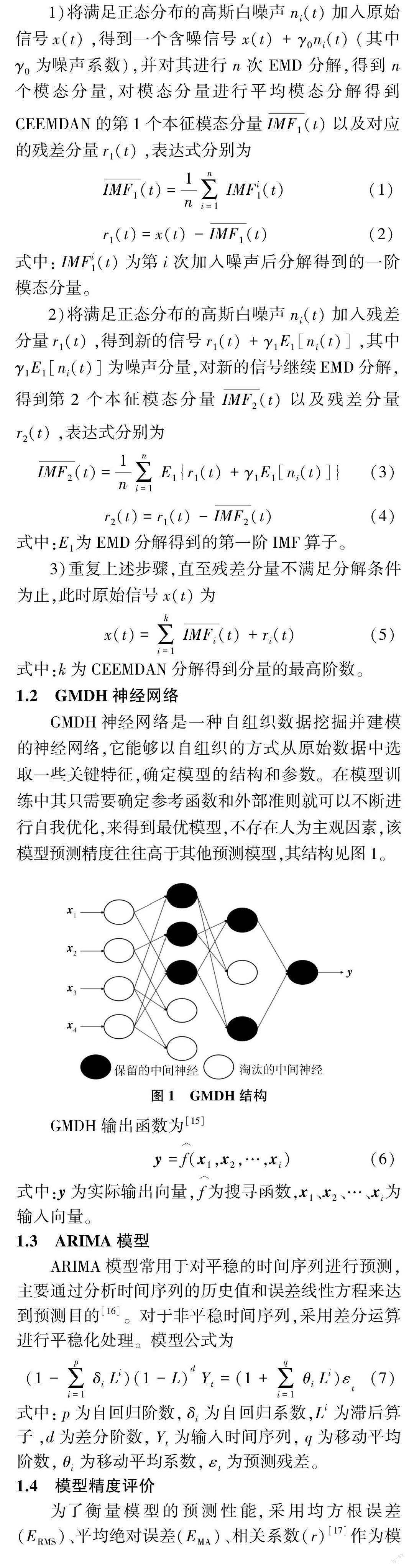
ＣＥＥＭＤＡＮ 算法是基于ＥＭＤ 和ＥＥＭＤ 改进的一种信号处理方法，主要通过在原始信号上添加自适应高斯白噪声，有效避免ＥＭＤ 的模态混叠现象，同时可以消除虚假信息干扰，使数据平稳化，算法实现主要步骤如下［１４］ 。

１．５ 大坝变形预测流程

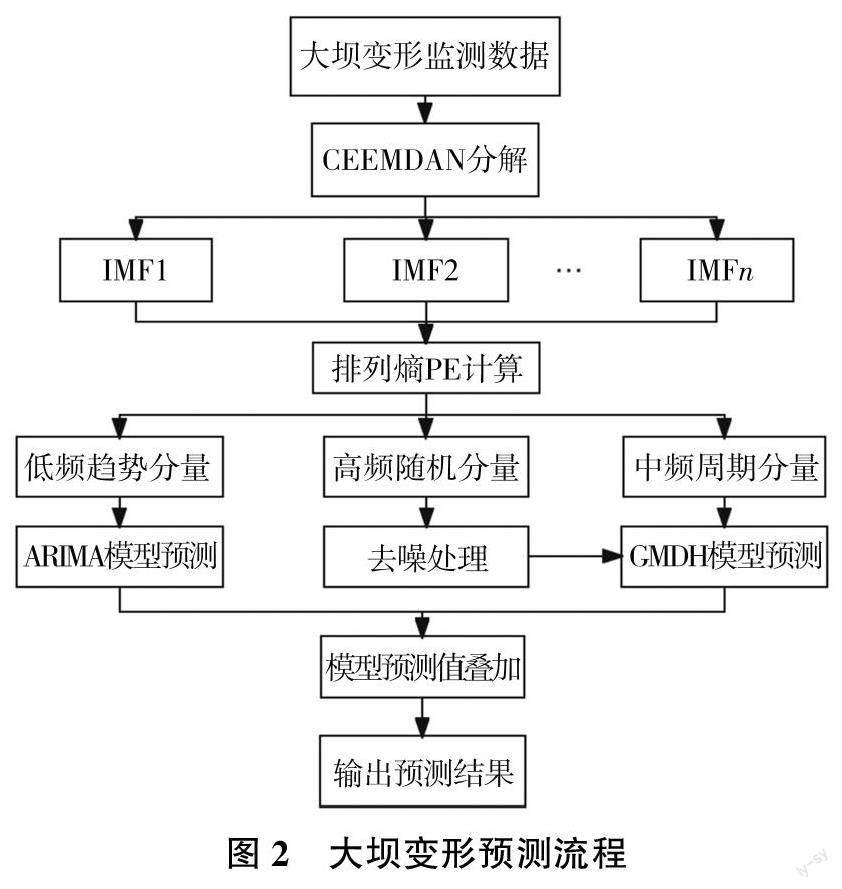
基于ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 的大坝变形预测流程见图２。首先进行数据预处理， 采用ＣＥＥＭＤＡＮ 算法对大坝变形原始数据进行分解得到不同频率的模态分量，利用排列熵算法（ＰＥ）进行筛选，得到高频随机分量、中频周期分量和低频趋势分量；再采用ＧＭＤＨ 模型对去噪处理后的高频随机分量和中频周期分量进行预测，采用ＡＲＩＭＡ 模型对低频趋势分量进行预测；最后将各模型预测结果叠加得到最终预测结果。

２ 工程应用

２．１ 水平位移监测数据

所选数据为江西上犹江水电站混凝土大坝２０１９ 年１１ 月１９ 日至２０２０ 年６ 月１ 日引张线监测点ＥＸ２ 水平位移监测数据，数据采样间隔为１ ｄ，共２００ ｄ 数据，把前１４０ ｄ 数据作为模型训练集、后６０ ｄ 数据作为预测数据的测试集。监测点ＥＸ２ 水平位移变化曲线见图３，发现水平位移数据具有明显的非线性和非平稳性特征。

２．２ 模型应用分析

对监测点ＥＸ２ 的水平位移数据进行ＣＥＥＭＤＡＮ分解，设置加入５００ 组高斯白噪声信号，标准差为０．２，分解得到８ 组不同频率尺度的ＩＭＦ 分量，见图４。

为筛选分解后的模态分量频率，参考文献［１８］的排列熵算法计算各模态分量的熵值，结果见图５。通过比较各个分量的相似性、接近程度和大小对各个分量进行分类重构。ＩＭＦ１ 至ＩＭＦ８ 的排列熵值逐渐递减，其频率逐渐降低，随机性逐渐减弱。ＩＭＦ１、ＩＭＦ２的熵值较大，具有明显的随机性，视为高频随机分量；ＩＭＦ３～ ＩＭＦ６ 熵值居中，视为中频周期分量； ＩＭＦ７、ＩＭＦ８ 的熵值较小，均小于０．２，视为低频趋势分量。

针对大坝变形数据的高频、中频、低频分量，分别构建ＧＭＤＨ 模型和ＡＲＩＭＡ 模型进行预测。高频分量主要受变形数据噪声的影响，参考文献［１９］中小波阈值法对高频分量进行去噪处理，高频分量ＩＭＦ１ 和ＩＭＦ２ 去噪前后对比见图６，原始数据降噪后的结果见图７。

利用ＧＭＤＨ 模型对去噪处理后的高频测试集分量和中频测试集分量进行预测，设置ＧＭＤＨ 模型网络层最大神经元数为２５，最大网络层数为５，压力系数为０，学习率为０．７。利用ＡＲＩＭＡ 模型对低频测试集分量进行预测，设置ＡＲＩＭＡ 模型的自回归项数为３，差分次数（阶数）为３，滑动平均项数为１。将所有预测结果相加得到最终的预测结果。

２．３ 模型预测性能对比

为验证ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 模型的预测性能，将其与ＢＰ 神经网络模型、ＲＢＦ 神经网络模型、ＧＭＤＨ 模型和ＣＥＥＭＤＡＮ－ＧＭＤＨ 模型进行对比。各模型的评估指标见表１。ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ模型的预测精度最高， 其Ｅ_ＲＭＳ、Ｅ_ＭＡ、ｒ 分别为０．０４８ ｍｍ、０．０３５ ｍｍ、０．９９４，均优于其他模型的评价指标，证明了该模型应用在大坝变形预测上的可行性。

各模型的预测值与实测值对比见图８。单独使用ＢＰ 神经网络模型和ＲＢＦ 神经网络模型分别进行预测，其预测结果与实测值具有明显的差异，误差较大；ＧＭＤＨ 模型预测结果趋势与实测值趋势一致，但具有明显的滞后性；采用ＣＥＥＭＤＡＮ 进行数据分解后再预测，ＣＥＥＭＤＡＮ－ＧＭＤＨ 模型预测效果得以提升；相比于以上模型，ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 模型预测效果最好，其预测曲线最贴合实测值曲线，波动周期大体一致，能够很好地体现监测点水平位移变化趋势。

ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 模型预测值与实测值的关系见图９，可以看出预测值与实测值吻合较好，体现出ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 大坝变形预测模型的有效性。

３ 结论

针对大坝变形数据的复杂性和非线性等特征，本文建立了ＣＥＥＭＤＡＮ－ＧＭＤＨ－ＡＲＩＭＡ 大坝变形预测模型，并通过工程实例进行实验分析，得到以下结论：

１）将ＣＥＥＭＤＡＮ 应用于大坝变形数据分解，有效降低了原始数据的复杂性，有利于大坝数据特征的分析及预测。

２）利用ＡＲＩＭＡ 模型擅长处理线性平稳性数据的优势，弥补ＧＭＤＨ 模型在线性分析上的不足，提高了模型预测精度。

３）通过工程实例应用表明，ＣＥＥＭＤＡＮ－ＧＭＤＨＡＲＩＭＡ模型的预测精度明显优于ＢＰ、ＲＢＦ、ＧＭＤＨ 和ＣＥＥＭＤＡＮ－ＧＭＤＨ 模型的，验证了该模型对大坝变形预测的准确性和可行性。

【责任编辑 栗铭】