基于改进Pinball 损失的支持向量机
2024-03-08孙雪莲姜志侠姜文翰
孙雪莲,姜志侠,姜文翰
(长春理工大学 数学与统计学院,长春 130022)
支持向量机(Support Vector Machine,SVM)是一种具有统计学与最优化理论支撑的经典机器学习方法,在处理小规模非线性数据上具有明显优势,因而被广泛使用到手写体识别、图像处理、文本识别等领域[1]。
1999 年,Suykens J 等人[2]提出了带有Hinge损失的支持向量机,该模型能够抓住关键样本,剔除冗余样本,保证了分类的准确性和泛化性能。但对错误分类和正确分类的样本施加相同程度的惩罚,使得模型对噪声数据敏感,降低模型分类的准确性。Huang 等人[3]将Hinge 损失替换为Pinball 损失,提出Pin-SVM。该模型将分位数距离作为目标函数,降低对正确分类的惩罚,导致支持向量机对噪声数据敏感性降低,提高了模型的鲁棒性。2015 年Huang 等人[4]利用SMO算法寻找Pin-SVM 及稀疏的Pin-SVM 全局最优解,令Pin-SVM 能够在现实情况下应用。2016 年Gong 等人[5]基于TSVH 和Pin-SVM 提出了TPSVH分类器,提高了分类性能,具有更高的稳定性。Shen 等人[6]在2017 年提出截断Pin-SVM 模型,该模型结合了Pin-SVM 和C-SVM 的优势,对噪声数据不敏感同时具有稀疏性。同年Xu 等人[7]提出带有Pinball 损失的孪生支持向量机。2020 年Liu 等人[8]提出了SpinNSVM 模型,该模型具有一个平滑的Pinball 损失函数,能够更好地拟合样本。2021 年Anand 等人[9]将特权信息加入Pin-SVM 模型中,提出了基于特权信息的双弹球支持向量机分类器(Pin-TWSVMPI),能够在相对较少的时间内提升模型的精度。
考虑到Pin-SVM 损失函数的参数取值范围,在Pin-SVM 的基础上提出了基于指数的损失函数,得到参数取值范围更广泛的Epin-SVM 模型,来提高模型分类的精度。并通过拉格朗日对偶等方法求解Epin-SVM 的目标函数与划分超平面。利用UCI 数据集进行算法性能测试,并在UCI 数据集加入5%和10%的噪声进行算法精度测试,实验结果表明Epin-SVM 算法在一定程度上能够提升算法分类精度。
1 带有Pinball 损失的SVM
支持向量机(SVM)算法是在样本空间中寻找支持向量,根据支持向量确定最优划分超平面,使不同类别样本之间间隔距离最大。在非线性的样本中,可以利用核技巧将样本特征映射到高维空间上,对非线性样本进行分类[10]。考虑二分类问题,样本集Z={xi,yi},i= 1,2,…,k,其中xi∈Rn为特征向量,yi∈{1,- 1}为分类标签,SVM 模型如下:
其中,C为惩罚参数;ξi为松弛变量。
由于支持向量机对噪声数据极其敏感,分类精度会因噪声数据下降,为提升模型预测精度,利用带有Pinball 损失的支持向量分类器,其分位数距离来度量边缘,最大化两类样本的分位数距离,降低支持向量机对噪声数据的敏感性[11]。Pinball 损失为l1损失函数,形式如下:
其中,u=yi(ω·xi+b);-τ≤τ≤1。
使用Pinball 损失函数的思想得到支持向量机模型如下:
当τ= 0 时,第二个约束变为ξi≥0,上式简化为支持向量机。
2 Epin-SVM 模型
本研究基于Pinball 损失函数提出Epinball 损失函数(仍记为Lτ(u)):
其中,u=yi(ω·xi+b);-1 ≤τ≤1。
使用Epinball 损失函数建立Epin-SVM 模型:
引入Lagrange 函数:
αi和βi为Lagrange 乘子,αi≥0,βi≥0,由拉格朗日函数对ω,b,ξi的导数为0,得到:
因而得到模型(5)的对偶问题:
引入核函数K(xi,xj) =φ(xi)Tφ(xj)[12],令υi=αi-βi,得到:
令υi*和βi*为对偶问题(9)的解,那么可得到模型(5)的解:
最终模型的决策函数为:
3 分类问题中Epinball 损失函数的性质
首先定义在X×Y上的概率测度为ρ,其中X∈Rn为输入空间,样本标签集合Y= {-1,1}。因而产生一个分类器C,使得X→Y的误差尽可能小:
其中,I为指标函数;ρX为ρ在X上的边际分布;ρ(y|x)为ρ在X处的条件分布;ρ(y|x)由P(y= -1|x)和P(y= 1|x)给出。贝叶斯分类器定义为:
为使:
设函数sgn(f):X→R诱导了一个二元分类器,那么误分类的误差表示如下:
其中,Lmis(μ)为误分类损失,定义为:
对于任何损失L,可测函数f的预期风险定义为:
使预期风险最小化[12],对于∀x∈X得到函数:
下面说明式(4)损失函数Lτ诱导了贝叶斯分类器。
定理:对于损失函数Lτ,使预期风险最小的可测函数fLτ,ρ等于贝叶斯分类器,即:
证明:当-1 ≤τ≤1 时有:
因此,当p(y= 1|x) <p(y= -1|x) 时,预期风险的最小值为2p(y= 1|x),此时t= -1。
当p(y= 1|x) =p(y= -1|x) 时,最小值为1,此时t为(-1,1)的任意值。
当p(y= 1|x) >p(y= -1|x) 时,最小值为2p(y= -1|x),此时t= 1。
因此得到:
即fLτ,ρ(x) =fC(x),∀x∈X。
4 实验
4.1 实验环境及实验数据
为验证Epin-SVM 算法的性能,利用8 个UCI数据集进行算法性能验证,数据集相关信息如表1 所示。利用网格搜索求得最佳模型参数C,模型采用高斯核函数和线性核函数。

表1 数据集相关信息
4.2 实验评估
本文采用的评价标准有准确率和F1 值。混淆矩阵[15]如表2 所示。

表2 混淆矩阵
评价指标定义为:
4.3 实验过程与结果分析
实验开始前,先对数据进行归一化,并在{2-7,2-6,…,2-6,27}中寻找参数C的最优值,并使用线性核函数与高斯核函数进行实验。此外实验随机分配测试集和训练集,两者所占比重为80%和20%。实验加入比例为5%和10%的噪声后的分类结果如表3 所示。

表3 基于线性核函数的不同SVM 分类准确率及F1 值
表3 中数据集分类精度对比显示,相较于传统支持向量机与Pin-SVM,当噪声比为0 时,Epin-SVM 在4 个数据集上精度有所提高,其他数据集上与Pin-SVM 分类精度持平,噪声比在5%时,Epin-SVM 在5 个数据集上精度提高1%左右,而噪声比在10%时,Epin-SVM 在2 个数据集精度有所提高,但WDBC 数据集上,相较于Pin-SVM 精度下降。本文猜想与数据集本身的分布有关。对不同算法进行了F1 值计算,Epin-SVM 在大部分数据集上F1 值较高,此外在噪声比为10%的Monks3 数据集上,相较于Pin-SVM 模型Epin-SVM 模型F1 值高,说明Epin-SVM 算法更优。而在表4 中显示,在高斯核函数下,Epin-SVM 在大部分UCI 数据集精度及F1 值与Pin-SVM 持平。在Monks3 和Cloud 数据集上,较Pin-SVM 精度有所提高。
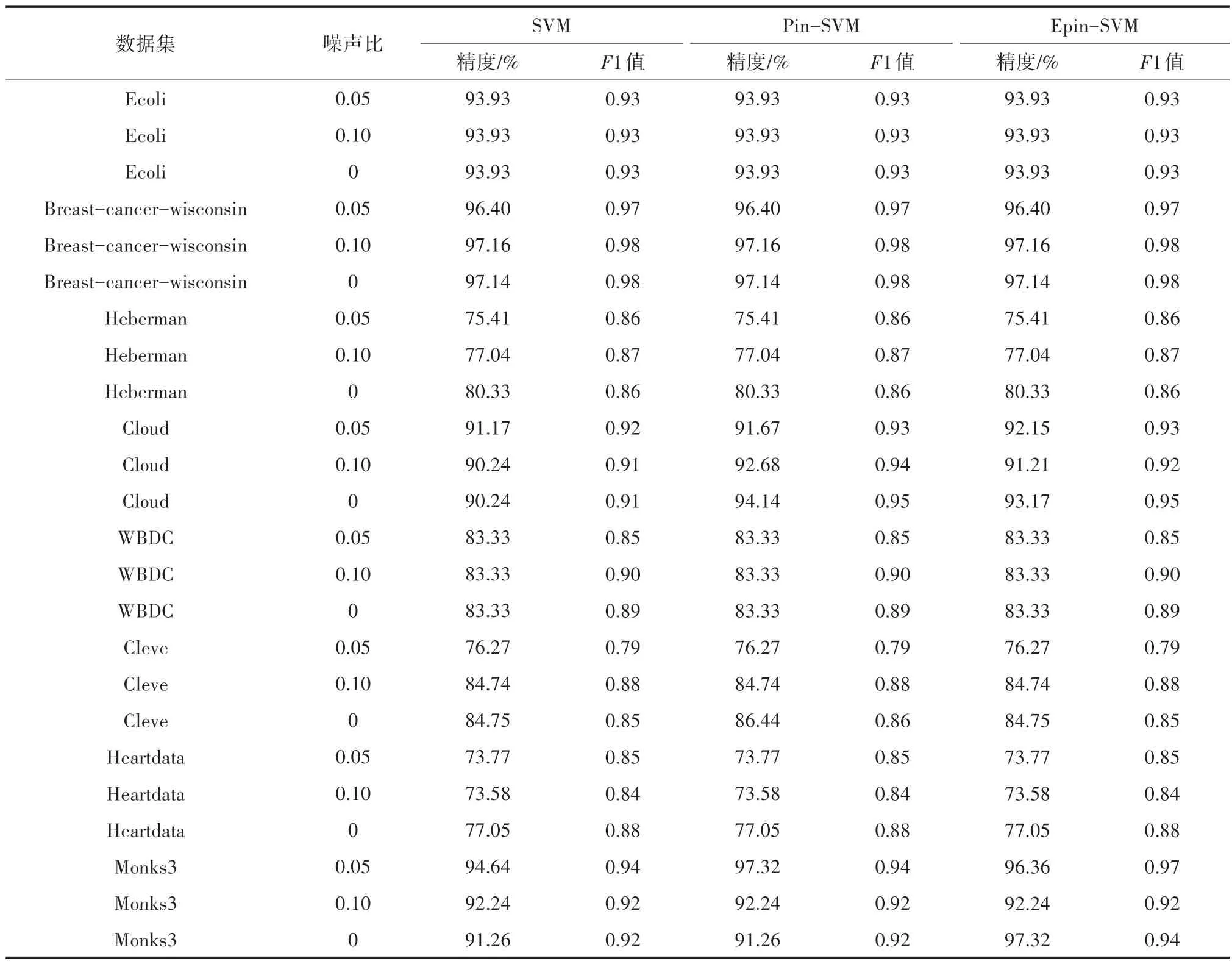
表4 基于高斯核函数的不同SVM 分类准确率及F1 值
图1 显示Epin-SVM 在τ∈[-1,1]时,UCI 数据集达到较高的分类精度。对于同一数据,Epin-SVM 在τ<0 区间内的可能得到更高的分类精度,相较于Pin-SVM 中τ值的范围进一步扩大,并使模型拥有更高的精度。

图1 不同τ 值下算法精度
5 结论
本文提出了Epin-SVM 模型,给出Epin-SVM模型的改进的合理性。在UCI 数据集上对模型分类精度进行验证,发现改进后的模型分类精度提高。在实验中发现Epin-SVM 在大数据集上运行时间有待提高,这将会是未来的研究方向。
