复合激励下两种类型电动汽车的行驶平顺性分析*

陈丽霞

(兰州石化职业技术大学 汽车工程学院,甘肃 兰州 730060)

0 引 言

纯电动汽车因其动力能源的清洁性、方便性、易操作控制等特点被大力推广,是当前汽车行业的重要发展方向[1-2]。常见的电动汽车驱动形式有集中电机驱动和轮毂电机驱动两种方式,研究多种路面激励下电动汽车不同驱动形式的振动机理,对其悬架系统进行动态性能改善、结构优化设计、减振降噪、可靠性应用等具有重要的理论意义。

很多学者对电动汽车行驶平顺性开展了大量的研究。谭迪[3]建立2-DOF集中驱动与轮毂驱动电动汽车模型,在单一路面激励下仿真分析了两种不同驱动形式下汽车的行驶平顺性。李燕超[4]建立三种电动汽车悬架模型,应用虚拟仿真技术研究汽车行驶过程中的运动特性。王佳圣[5]利用Adams/Car软件开展随机激励和脉冲激励下后置驱动电机的纯电动汽车平顺性优化研究。王晟[6]在路面激励与电机激励下,以电驱动桥商用汽车为研究对象,分析优化车辆不确定性参数下车身结构和悬架的振动特性。杨蔚华[7]基于半主动悬架原理,以电动轮汽车为研究对象,针对电动汽车因电磁垂向振动引起的平顺性降低问题,深入开展电动轮汽车的振动控制研究。虽然现有研究已经建立了各种影响因素下的电动汽车模型,其振动性能也被广泛研究,但不同路面激励下的集中电机驱动和轮毂电机驱动汽车平顺性对比分析研究较少;且对于电动汽车在匀速和加速两种工况下,多种路面激励与电机电磁复合激励对汽车振动性能的影响等方面鲜有研究。

基于上述研究分析,考虑电动汽车行驶过程中的实际路况以及驱动电机电磁激励产生的垂向振动等情况,笔者建立了多种路面激励与电机电磁复合激励下的轮毂电机驱动和集中电机驱动1/2、4-DOF模型,运用四阶Variable-steplength Runge-Kutta和傅里叶变换法求解模型,借助时域图和PSD方法,从时域和频域两方面对比分析两种电动汽车驱动形式对汽车平顺性的影响,为电动汽车系统行驶平顺性评价与控制、减振降噪等奠定理论基础。

1 建立1/2、4-DOF轮毂电机驱动汽车模型

假设汽车对称于其纵轴线且左、右车辙不平度函数相等,考虑车辆垂向振动和俯仰振动,建立路面-电磁复合激励下1/2、4-DOF轮毂电机驱动电动汽车模型,如图1所示。将该模型中电机md移到m0位置,得到集中电机驱动模型。m0,m1f,m1r,md分别为车身质量,左前、左后轮质量,驱动电机质量;Iy为车身转动惯量;k1f,k1r,k2f,k2r分别为左前、左后轮刚度,前、后悬架刚度;c2f,c2r分别为前、后悬架阻尼;z0,z1,z2分别为车身垂向位移,左前、左后轮垂向位移;θ为车身度仰角;qf,qr为前、后车轮路面激励;a为前轴距质心距离,b为后轴距质心距离;Ftf,Ftr分别为前轮轮毂电机激励,后轮轮毂电机激励。各参数取值如表1所列。

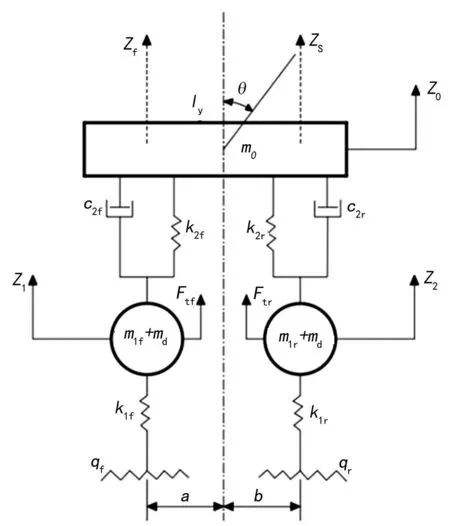
图1 1/2、4-DOF轮毂电机驱动汽车模型

然后,基于Lagrange方程对文中轮毂电机驱动的汽车模型进行计算。1/2、4-DOF轮毂电机驱动电动汽车模型的振动微分方程如式(1)所列,转变为矩阵形式如(2)所列。

(1)

(2)

其中:

[M]=diag[m0Iy(md+m1f)(md+m1r)]

[C]=

[K]=

2 两种路面激励模型与电机垂向电磁激振力

2.1 随机路面激励时域模型

匀速工况时,左前车轮随机路面激励模型可以采用线性滤波白噪声法得到[8]:

(3)

式中:qf为路面位移;Gq(n0)为路面不平度系数;v为车辆行驶速度;w(t)为均值为0的单位白噪声;n0=0.1 m-1,为参考空间频率;n00=0.011 Hz,为下截止空间频率。汽车左后车轮路面激励与左前车轮路面激励的关系如式(4)所示,其中τ=L/v,L为汽车轴距。由此推导出左后车轮随机路面激励模型如式(5)所示。

qr(t)=qf(t-τ)

(4)

(5)

2.2 三角形凸块脉冲激励

汽车行驶中,遇到的弓形、圆形凸起路面会对汽车造成离散事件[9],国标GB/T4970-2009中规定,采用三角形凸块来描述路面脉冲激励,如图2所示。其中凸块的长度和高度分别规定为l=400 mm、h=120 mm;脉冲路面左前车轮激励qf(t)如式(6)所示,t0为前轮距离三角凸块时间。前、后车轮脉冲路面激励关系式同式(4)。

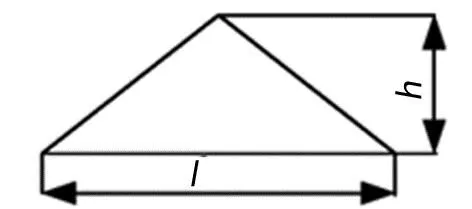
图2 三角形凸块

qf(t)=

(6)

2.3 电机垂向电磁激振力

轮毂盘式永磁直流电机的垂向电机电磁激振力Ft(f)可由式(7)计算得到[10]。

(7)

式中:n是电机转速;R是电机定子平均半径;z是正整数;激振力作用周期T=60/(nm),m是电机极数。

电磁转矩Tem可由式(8)计算得出。

(8)

式中:极弧系数αi=2/π,气隙磁密幅值Bδ=0.7T;w为绕组相数;N定子绕组每相线圈匝数;Iφ为电流有效值;Do和Di分别为永磁体的外径和内径。各参数取值如表1所列。

设汽车在C级路面上匀速行驶速度v=30 m/s,电机驱动转速n=308 r/min,仿真分析前、后车轮随机路面激励,三角形脉冲激励及电机垂向电磁激振力随时间变化图,如图3所示。

图3 路面激励与电机垂向电磁激振力时间历程图

3 集中电机驱动和轮毂电机驱动汽车时域特性对比分析

设汽车匀速行驶在C级路面上,将随机路面激励、三角形脉冲激励及电机垂向电磁激振力模型表达式分别代入系统方程中,对1/2、4-DOF集中电机驱动和轮毂电机驱动电动汽车模型进行时域仿真,得到v=30 m/s时“随机路面激励+电磁激励”、“三角形脉冲激励+电磁激励”下两种模型的平顺性评价指标时间历程图,如图4～5所示。

图4 “随机路面+电磁”复合激励下汽车行驶平顺性对比分析

文中只讨论前轮动载荷和前悬架动挠度时间历程图。由图4(a)、(b)加速度变化幅值可以得出:就乘客乘坐舒适性而言,在随机激励+电磁激振力双重激励下,轮毂电机驱动模型优于集中电机驱动模型。但由于轮毂电机驱动模型中非簧载质量增加,轮毂电机驱动模型中前轮动载荷的振动幅值明显高于集中电机驱动模型,车轮与路面间的附着效果变差,降低了轮胎的接地性,如图4(c)所示。图4(d)中轮毂电机驱动模型对前悬架动挠度的影响趋势相较于车身、轮胎的振动量变化较小,但也有一定程度的恶化。由此得出,轮毂电机驱动模型对汽车平顺性指标的影响程度依次为车轮动载荷>悬架动挠度>车身垂向加速度>车身俯仰角加速度变化;集中电机驱动模型对汽车平顺性指标的影响程度依次为车身垂向加速度>车身俯仰角加速度>车轮动载荷>悬架动挠度。

图5为考虑电机电磁激振力时两种驱动模型汽车以30 m/s速度匀速通过三角形凸块时汽车各平顺性评价指标的时间历程图。

图5 “三角形脉冲+电磁”复合激励下汽车行驶平顺性对比分析

图5(a)、(b)中轮毂电机驱动汽车模型车身垂向加速度和车身俯仰角加速度的振动幅值变化范围分别为[-1.6,1.8],[-1.2,1.7],相比集中电机驱动模型,其振动幅值降低57%,且轮毂电机驱动模型振动衰减平缓,乘坐舒适性相对较好。图5(c)中轮毂电机驱动模型的前轮动载荷正向振动幅值低于集中电机驱动模型对应的正向振动幅值,但车轮的负向振动幅值比集中电机驱动模型增加46.6%。图5(d)中集中电机驱动模型对应的前悬架动挠度最大振幅值为0.032 m,比轮毂电机驱动模型对应的最大振幅增加48.4%,说明集中电机驱动模型撞击悬架限位块的概率大于轮毂电机驱动模型,这必然会降低汽车行驶平顺性。

4 集中电机驱动和轮毂电机驱动汽车频域特性对比分析

根据机械振动原理,有必要对文中所建模型的频域特性加以研究,原因在于机械振动对汽车平顺性的影响除了与振动持续时间有关外,也与振动的频率有关。非平稳工况下汽车受到的路面随机激励在空间域内是平稳的,在时间域内是非平稳的;但由于空间域内振动系统的微分方程为时变微分方程,所以振动系统的输出响应在时间域和空间域上均是非平稳的。文中采用瞬态空间频响函数法,推导系统响应的瞬态空间频率响应函数H(s,n)计算公式[8],令汽车在C级随机路面激励下,以v0=5 m/s,a=2 m/s2的车速起步加速行驶,仿真分析汽车行驶到s=150 m时各响应量对应的瞬时空间功率谱密度图,如图6所示。

图6 非平稳随机路面激励下汽车频域特性对比分析

各部分固有频率计算公式为:

(9)

时间频率f与空间频率n的关系式为:

f=nv

(10)

集中电机驱动模型车身质心处的固有频率为0.048 m-1,轮毂电机驱动模型车身质心处的固有频率0.050 m-1,前轮固有频率为0.438 3 m-1。

图6(a)、(b)中,在0～0.15 m-1的空间低频区域内,两种电动汽车驱动模型对应的车身垂向加速度PSD和车身俯仰角加速度PSD曲线变化规律一致;但图6(b)中轮毂电机驱动模型引起的车身俯仰角加速度PSD最大振幅比集中电机驱动模型高出18%,说明在此模型下克服车身俯仰角振动需要的能量较多;在0.15～0.4 m-1空间频率范围内,轮毂电机驱动模型对应的车身垂向加速度和车身俯仰角加速度PSD曲线先急剧增大后减小,而集中电机驱动模型对应的车身垂向加速度和车身俯仰角加速度PSD曲线在此范围内平稳增大,在车轮固有频率处出现最大峰值,容易引起车轮共振。图6(c)中,在0～0.4 m-1空间频率范围内,轮毂电机驱动模型对前轮相对动载荷PSD的影响远大于集中电机驱动模型产生的影响,说明在此空间频率范围内,轮毂电机驱动模型克服车轮振动需要的能量要大于集中电机驱动模型克服振动所需的能量;振动频率大于0.4 m-1后,两种电机驱动模型对前轮相对动载荷PSD的影响逐渐减小,但集中电机驱动模型对应的PSD曲线值相对较大。图6(d)中,在0～0.15 m-1的低频区域,两种模型对应的悬架动挠度PSD曲线变化趋势一致,均会在车身质心固有频率处引起共振现象,但集中电机驱动模型对应的悬架动挠度PSD振幅较大,说明在此模型下克服悬架振动需要的能力较大。

5 结 论

文中建立了两种路面激励与电机电磁复合激励下的轮毂电机驱动和集中电机驱动1/2、4-DOF模型,运用Variable-step length Runge-Kutta和瞬态空间频响函数法求解模型,从时域和频域两方面对比研究了两种电动汽车驱动形式对汽车平顺性影响,揭示了不同路面激励、不同行驶工况下两种汽车驱动模型的时域和频域响应量动力学变化规律。结论如下。

(1) 建立的1/2,4-DOF电动汽车模型考虑了随机路面激励、三角形脉冲激励和电磁垂向激励力,所建模型更贴近工程实际;考虑了汽车匀速和起步加速行驶工况,贴近汽车真实行驶路况,研究结果更具理论参考价值。

(2) 时域特性分析结果表明,随机路面激励+电磁激振复合激励下,轮毂电机驱动模型对车轮动载荷的影响显著大于集中电机驱动汽车模型;该模型对车身加速度和车身俯仰角加速度的影响程度低于集中电机驱动模型;两种模型对应的悬架动挠度曲线差值很小。三角形脉冲激励+电磁激振复合激励下两种驱动模型对应的悬架动挠度振动幅值差较大,其他响应量变化规律与随机路面激励下各响应量变化规律相似。

(3) 频域特性分析结果表明,轮毂电机驱动模型对车身加速、车身俯仰角加速度、车轮相对动载荷PSD的影响远大于集中电机驱动模型对应的响应量PSD;两种模型对悬架动挠度PSD影响差别很小。综上所述,轮毂电机驱动汽车因其非簧载质量增加而加剧轮胎跳动,降低了车轮与路面间的附着效果,对汽车的接地性与行驶平顺性产生了显著的不利影响。