精心创设情境式任务 促进乘法模型整体建构

李晓梅

（江苏省泰兴市教师发展中心）

《义务教育数学课程标准（2022 年版）》（以下通称“新课标”）要求学生“在具体情境中，利用乘法表示数量之间的关系，建立乘法模型，知道模型中数量的意义。”要求教师“重视单元整体教学设计，改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联。”为此，教师要结合教学需要，精心创设情境式任务，有效驱动学生经历建模过程，整体建构乘法模型。

一、创设探究性情境式任务，促进课时整体乘法模型建构

学生的探究离不开教师的引导。教师要根据学生的已有经验和认知特点，精心创设探究性情境式任务，驱动学生积极、主动地进行探究，以沟通新旧知识之间的联系，促进课时整体乘法模型建构。在以任务为驱动的小学数学课堂上，教师要注重探究性情境式任务的设计，引导学生在情境探究的过程中找到科学的学习数学的方法，培养学生自主学习的意识和能力。除了以学生个人为单位制订活动计划之外，教师也可以设计使学生小组合作的探究性情境式任务，引导学生与同伴相互配合，在共同协作的同时掌握数学知识，并实现合作意识和合作能力的提升。为此，教师要努力为学生提供探究的时间和空间，为学生的积极探究创造机会，为学生整体建构乘法模型提供保障。尤其是当学生探究遇到困难时，教师要给学生提供恰当的指导意见，引导学生在探究中自主发现问题、矫正问题。

例如，在教学“常见的数量关系”时，教师课始可以借助课件创设一个探究性情境式任务：某高速路旁有这样一个标志（见下页图1）。王老师在这条高速路上开车3小时，行驶了240千米。他有没有超速？

图1 某高速路旁的标志

学生根据教师创设的探究性情境式任务，先认识交通标志的含义（限速80千米，说明汽车1小时最多只能行驶80千米），接着，认识汽车仪表盘（见图2）。

图2 汽车仪表盘

学生根据已有经验说明汽车速度快、慢时仪表盘指针的变化情况，再一起认识“km/h”中“km”“h”“/”和“km/h”的意思及其读法。有的学生根据算式240÷3=80千米/小时，判断出王老师没有超速；有的学生认为80千米/小时是平均速度，实际开车可能会有时快有时慢，如果速度超过80千米/小时，王老师就超速，从而引出求汽车平均速度的方法——用汽车行驶的千米数除以汽车行驶的时间（即路程÷时间=速度）。学生从口算骑自行车、直升机飞行以及卫星在太空运行的平均速度中初步感知路程、时间、速度三者之间的关系。在此基础上，教师追问：“如果王老师按80千米/小时的速度开车2 小时，能行驶多少千米？如果这辆汽车要行驶320千米，需要多长时间？”学生从中发现“路程÷时间=速度”“速度×时间=路程”“路程÷速度=时间”都表示路程、速度和时间之间的关系。学生探究“求路程用乘法的理由”（速度相当于每份数，时间相当于份数，路程相当于总数量，要求“几个几是多少”用乘法）后，看图写算式（见图3），并思考：如果把这个问题看作走路问题，就该把哪个数量看作速度？把哪个数量看作时间？把哪个数量看作路程？如果把表1中的问题看作走路问题，该分别把哪个数量看作速度、时间和路程，为什么？

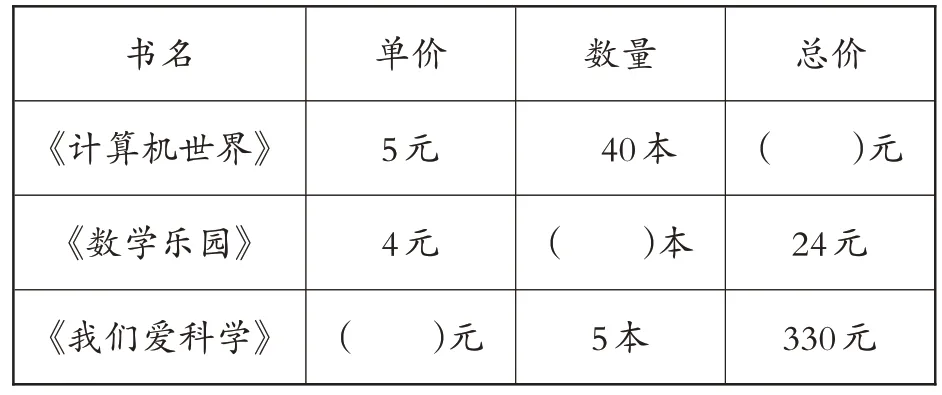
表1 问题情境

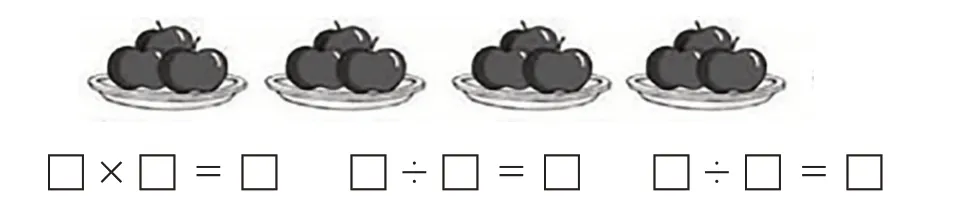
图3 看图写算式

教师联系学生实际生活创设探究性情境式任务，驱动学生亲身经历把实际问题抽象成数学模型并解释的探究过程。这个探究过程就是学生整体建构乘法模型的过程。为了完成教师创设的探究性情境式任务，学生透过现象看本质，发现数量之间的内在联系。“单价×数量=总价”和“速度×时间=路程”都是“几个几相加”的乘法意义的具体化，每组数量关系都能把“一类”关系的结构特点和本质联系明确而清晰地表达出来。为了沟通知识之间的联系，教师不但引导学生思考为什么求速度和时间时用除法、求路程时用乘法，而且引导学生在解决简单的实际问题中进行适当拓展。学生用同一个情境的不同种素材引出三组关系，具有一定的整体性和连贯性；教师引导学生把熟悉的看图写算式和单价、数量与总价问题看作“路程问题”，使其具备了模型的价值。教师这样整体建构乘法模型并适当拓展，帮助学生形成了对所建构乘法模型的全面认识。

二、创设故事性情境式任务，促进单元整体乘法模型建构

听故事是小学生喜闻乐见的活动形式之一。教师创设故事性情境式任务，驱动学生单元整体构建乘法模型，有助于激发学生的学习兴趣。故事可以是历史故事，可以是数学故事，也可以是时事性故事，只要是和教学内容有关，符合学生的认知特点，能有效驱动学生单元整体建构乘法模型的故事就可以。为此，教师要精心设计故事性情境式任务，使学生自然而然地听故事，并在听故事中产生一种不完成任务就放不下的冲动。当然，教师要基于单元整体的视角创设任务，就要充分研读整个单元的教学内容，帮助学生创设故事性情境式任务群，环环紧扣，层层推进，构建单元整体建模教学路径，促进学生在故事性情境式任务群的完成过程中形成和发展数学核心素养。

苏教版数学教材三年级下册第一单元“两位数乘两位数”中共有6 个例题，分别是口算两位数乘10（包括几十乘几十）、估算两位数乘两位数、笔算不进位的两位数乘两位数、笔算需要进位的两位数乘两位数、笔算两位数乘几十、两步连乘解决的实际问题等内容。教材中的情境式任务分别是：买菜椒送给养老院，购买马铃薯把蒜头装在同样大的袋子里，购买“迷你”南瓜，购买足球，购买乒乓球，这些任务虽然能引导学生顺利构建乘法模型，但这些任务之间联系不大，显得比较零散。

为了引导学生从单元整体建构乘法模型，教师可以把这些任务整合到“超市购物”故事主题任务中。教师可以这样设计故事性情境式任务：王老师和李老师一起去超市为学校购物。教师先引导学生猜一猜两位老师要购买哪些商品，再出示王老师购买菜椒、马铃薯和“迷你”南瓜的场景图以及李老师购买足球和乒乓球的场景图：（1）王老师给食堂买菜，先买了10 盒菜椒，每盒12 个；又买了40 袋马铃薯（其中5 袋马铃薯的质量见表2）；还买了12 箱“迷你”南瓜，每箱24个。（如果买53箱呢？）（2）李老师给体育室买足球和乒乓球：足球每个32 元，买了30 个这样的足球；买了6袋乒乓球，每袋5个，每个乒乓球2 元。然后，教师引导学生根据这些信息提出问题。学生根据题目中的信息很快提出相应的数学问题，如一共买了多少个菜椒？一共买了多少千克马铃薯？一共买了多少个“迷你”南瓜？买足球一共用了多少元？一共买了多少个乒乓球？买一袋乒乓球要用多少元？买乒乓球一共要用多少元？

表2 5袋马铃薯的质量

教师引导学生根据相关信息，按课时分别总结出数量关系并建构乘法模型——每盒菜椒的个数×盒数=菜椒的总个数、每袋马铃薯的质量×袋数=马铃薯的总质量、每箱“迷你”南瓜的个数×箱数=“迷你”南瓜的总个数、每个足球的钱数×个数=买足球要用的总钱数、每个乒乓球的钱数×一袋乒乓球的个数=买一袋乒乓球的钱数、每袋乒乓球的个数×袋数=买乒乓球的总个数，每个乒乓球的钱数×乒乓球的总个数=买乒乓球要用的总钱数。最后，教师引导学生把这些模型整体建构为统一的乘法模型——每份数×份数=总数。

“两位数乘两位数”是学生在理解并掌握“两位数乘一位数”基础上进行学习的内容。“两位数乘两位数”的算法是学生迁移应用到解决“三位数乘两位数”“三位数乘三位数”的问题的基础。为此，“两位数乘两位数”是整数乘法教学的关键。教师用故事形式把本单元的所有教学内容都“压缩”在一个比较综合的故事性情境式任务中，一方面是整合教材中的6个任务，形成一个有联系的任务群，使学生直观感知数学知识之间是相互联系的，另一方面有助于学生整体构建统一的乘法模型“每份数×份数=总数”。

其中，“买一盒乒乓球要多少元？”和“买乒乓球一共要用多少元？”两个问题既有联系，又有区别：两个问题都可以用相同的数量关系式“每个乒乓球的钱数×乒乓球的个数=买乒乓球的钱数”来解决，但前一个乒乓球的个数是一盒乒乓球的个数，后一个乒乓球的个数是乒乓球的总个数（或者说是6 袋乒乓球的个数）。求6 袋乒乓球的个数，要根据数量关系“每袋乒乓球的个数×袋数=乒乓球的总个数”进行计算。当然，后一个问题也可以根据前一个问题的结果进行计算，用“每袋乒乓球的钱数×总袋数=买乒乓球的总钱数”解决问题。也就是说，后一个问题要两次运用乘法模型，并且都可以用统一的乘法模型进行表达。

三、创设挑战性情境式任务，结构化梳理整体乘法模型

学生学习的乘法模型往往是点状的、零散的，教师有必要在最后的学习阶段，引导学生对乘法模型进行结构化梳理，帮助学生进一步理解数量关系的数学本质和内在关联，提高学生解决问题的能力。在复习“数与代数”时，教师可以用挑战性情境式学习任务驱动学生主动、积极地结构化梳理乘法模型。挑战性任务是一项能激发学生好奇心、好胜心、成功欲的，有明确目标且需要担负责任的任务。教师有针对性地创设挑战性情境式任务的难易度要适当：如果任务太难，学生无法完成；如果任务太简单，学生没有兴趣完成。对小学生而言，最适宜的挑战性情境式任务是学生“跳一跳能够得到的”，也就是在学生思维“最近发展区”的任务。教师要创设适合学生的、个性化的挑战性任务，使每个学生都能积极、主动地建构乘法模型。

课前，教师可以创设这样一个挑战性情境式任务：整理一下自己在整个小学阶段所学过的用乘法表示的数量关系。对于这个任务，每个学生都能或多或少地完成。学生经过整理，梳理出来的数量关系包括“每份数×份数=总数”“1倍量×倍数=倍数对应的数量”“每辆车乘坐的人数×辆数=乘坐的总人数”“每组的人数×组数=全班的总人数”“每人浇树的棵数×人数=浇树的总棵数”“单价×数量=总价”“速度×时间=路程”“工作效率×工作时间=工作总量”“单位‘1’的量×（百）分率=（百）分率所对应的数量”“本金×利率=利息”“收入×税率=纳税额”“原价×折扣=现价”等。这些数量关系在解决实际问题的过程中可以衍生出新的数量关系，如总价÷单价=数量、总价÷数量=单价、路程÷速度=时间以及路程÷时间=速度等。最终，学生发现总价、路程等都是积，单价、数量、速度和时间等都是因数，学生可以用一般性式子表示乘法模型——一个因数×另一个因数=积，并且可以根据“积÷一个因数=另一个因数”推理出其他数量关系式（见图4）。

图4 数量关系

教师引导学生自主整理所学过的用乘法表示的数量关系，这对小学生而言具有一定挑战性——乘法表示的数量关系分散安排在各册教材，并且按照循序渐进、螺旋上升的原则随着知识发展而不断变化。教学中，笔者发现每个学生都能完成这个挑战性任务，区别在于完成任务的数量和质量。教师如果能引导学生用思维导图加工整理这些内容，就能促进学生沟通知识的联系，把零散的知识点构成一个具有有机联系的知识网络，使学生在融会贯通中理解和掌握乘法模型，自主形成属于自己的认知结构。全面、整体地建构乘法模型，能帮助学生沟通新旧知识间的联系，把一个个零散、孤立的数学模型有机统一起来，形成一般化的数学模型，使学生在知识形成过程中把新知纳入已有知识体系并形成新的认知结构。

总之，情境式教学和任务驱动教学相结合，能使教学任务生动化、形象化、趣味化。教师精心创设的情境式任务是驱动学生整体建构乘法模型的“触发器”。情境式任务驱动学生从整体、系统、关联和结构化的视角推进乘法模型的整体建构，有助于学生更加形象、生动地感受数学的学科魅力，提高整体建构乘法模型的效率；有助于学生在深刻理解乘法模型中逐渐形成和发展数学核心素养。