水下管汇入水冲击数值模拟研究

曹先凡，王姝媛，王 琮，张爱霞，姚志广

1.中国石油集团海洋工程有限公司，天津 300451

2.中国石油天然气集团海洋工程重点实验室，天津 300451

3.中国石油天然气销售公司，北京 100007

水下管汇是海洋工程的重要组成部分，其安装下放时固定于框架之上，入水阶段受到海水的冲击，框架强度安全是保证其顺利就位的关键因素。海水冲击下管汇框架的响应分析需要考虑框架和海水之间的流固耦合作用。拉格朗日分析（Lagrangian analysis）中材料与网格关联，适用于结构变形的模拟。欧拉分析（Eulerian analysis）方法中网格固定，材料在单元间流动，可有效解决流体问题。管汇入水需要考虑结构和流体交界面模拟问题，耦合欧拉-拉格朗日算法（CEL）通过欧拉-拉格朗日的定义和求解成为解决该问题的重要手段。通用有限元软件ABAQUS 开发的CEL 模块已经被广泛应用于汽车、航天及海洋工程等众多领域，该模块可以模拟固体-泥土[1-6]、固体-液体[7-11]、固体-空气[12-17]之间的相互作用。

本文基于ABAQUS CEL 数值模拟方法，对管汇入水时框架的响应进行数值模拟研究，为管汇下放安全提供技术支持。

1 数值模型

针对管汇下放工况中框架受力特点建立有限元模型：框架底层承受入水冲击载荷，可选取底层主要结构进行入水过程的数值模拟，本文管汇框架底层主要由两种工字梁构成，选取这两种工字梁进行了建模；管汇框架入水受到冲击后，入水速度低于上部吊钩下放速度，此时管汇框架不承受吊索拉力作用，因此，模拟不考虑吊索拉力。在该模型中工字梁采用拉格朗日网格，海水采用欧拉网格。

1.1 整体模型构建

管汇框架入水相关的主要模型有：工字梁、海水域。以下给出整体模型的构建过程。

1.1.1 管汇框架底层主要工字梁模拟

管汇框架如图1所示，其底部工字梁分为两类：H440 和H300，最大跨度为4.05 m。所建工字梁模型如图2所示，腹板和翼板采用壳单元模拟，主要参数见表1。设置工字梁入水初始速度为1.00 m/s。

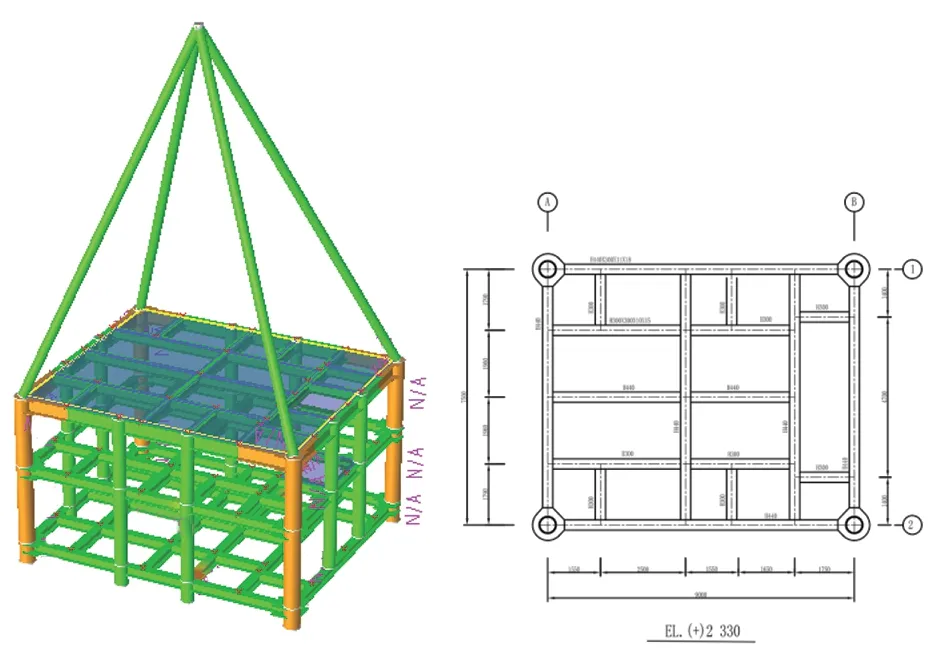
图1 管汇框架示意

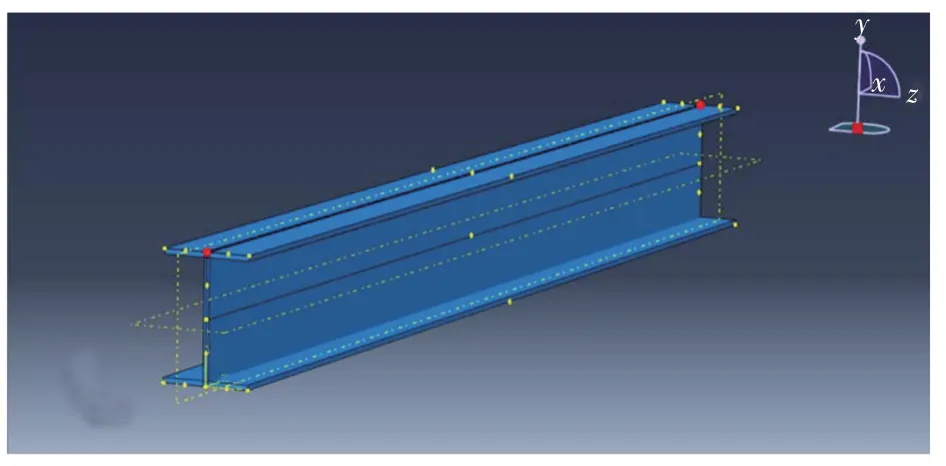
图2 工字梁模型（H440）

1.1.2 欧拉域及初始海水域

欧拉域及初始海水域见图3，欧拉域为整个长方体，采用欧拉网格离散。欧拉域由海平面分为两部分，海平面以下为初始海水域。为消弱边界影响，初始海水域的长度约为工字梁长度的3 倍，水深约为工字梁高度的3倍，欧拉域及初始海水域的主要尺寸见表2，海水主要参数见表3。海水建模为一种几乎不可压缩的黏性牛顿流体，采用线性Us-Up状态方程描述。

图3 欧拉域及初始海水域设置

表2 欧拉域及海水域主要尺寸

表3 海水主要参数

水介质的体积强度及静水状态体积响应特性定义如下：

式中：p为压强，Pa；ρ0为参考密度，kg/m3；c0为水中声速，m/s；η为名义体积压缩应变，η= 1-ρ0/ρ；Γ0为Gruneisen 常数，无量纲；Em为单位质量的内能，N·m/kg；s为无量纲系数，c0和s定义冲击波速度Us和粒子速度Up之间的线性关系如下：

水黏性剪切性质定义如下：

式中：S为应力偏量，Pa；为应变率偏量，s-1；μ为动力黏度，Pa·s；为工程偏应变率，s-1。

1.1.3 模型组装

将工字梁和欧拉域装配至1个模型，见图4。

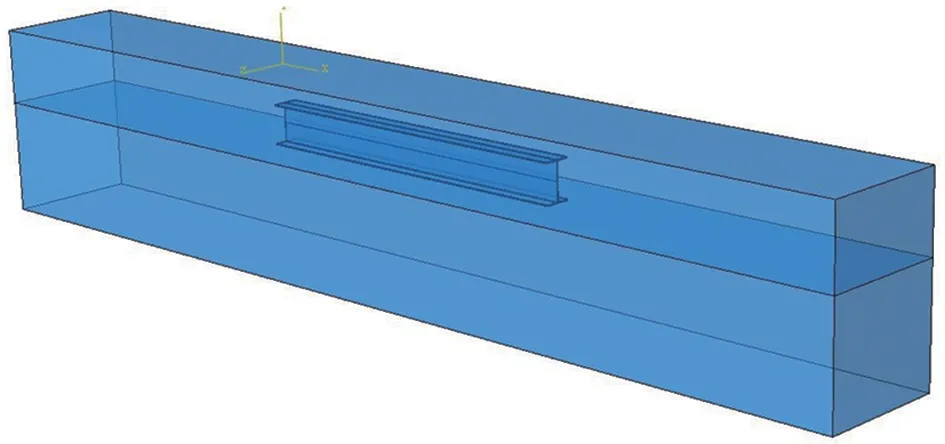
图4 组装模型示意

1.2 管汇质量影响分析及载荷施加

管汇及框架入水时，框架除了承受管汇产生的重力作用外，还应考虑管汇质量在动力分析中的作用。本文通过等效质量的方式考虑了管汇质量的影响，即框架的等效质量与框架、管汇质量之和相同，然后将框架等效质量均匀分布在各个工字梁上。在数值模型中通过设置材料密度计算等效质量。

2 模拟结果

通过数值模型模拟了管汇框架工字梁入水过程，给出了工字梁的速度变化和应力，分析了入水速度对工字梁应力的影响。

2.1 入水过程

图5给出了工字梁入水的过程。

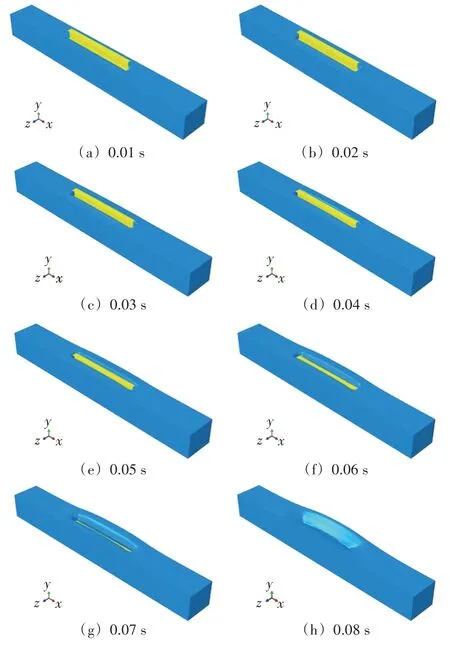
图5 工字梁入水过程

2.2 速度-时间历程

图6 为下放速度为-1 m/s 时工字梁下翼板中点竖向速度与时间的关系曲线，可以看出工字梁在与水面接触后，速度由1 m/s 降低至0.97 m/s，在0.002 s 以后速度超过1 m/s。说明工字梁即使有吊索约束，在此阶段也不承受吊索拉力。

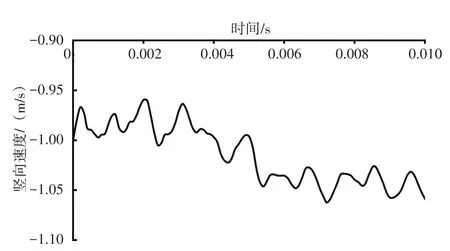
图6 工字梁下翼板中点竖向速度与时间的关系

2.3 应力分析

针对H440 工字梁下放，计算了不同时刻应力场。对于工字梁下翼板中点给出了应力随时间的变化（见图7），可以看出应力呈现两个级别的周期变化，短周期约0.003 5 s，长周期约0.03 s，最大应力出现在第一个短周期内，为38.45 MPa。图8给出了0～0.004 s内的工字梁应力分布。

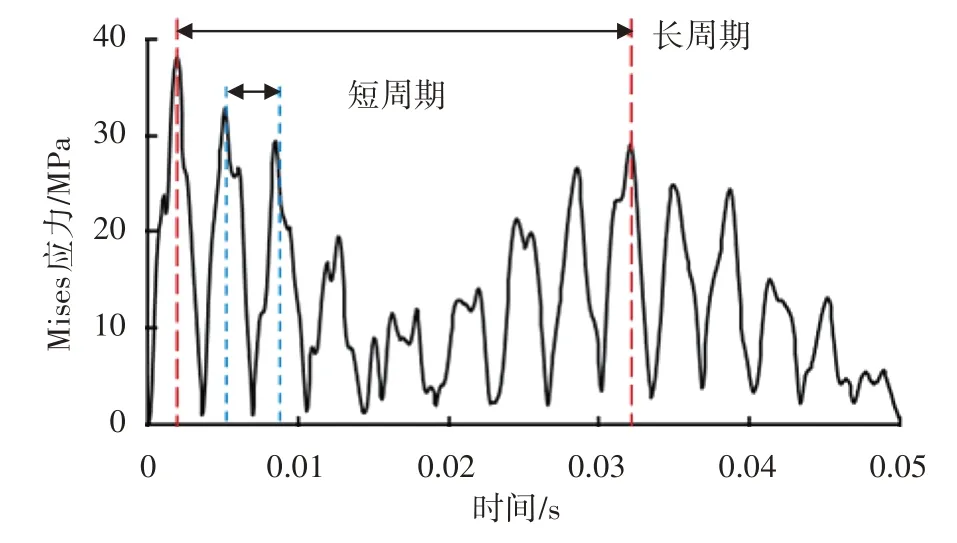
图7 工字梁下翼板中点应力与时间的关系

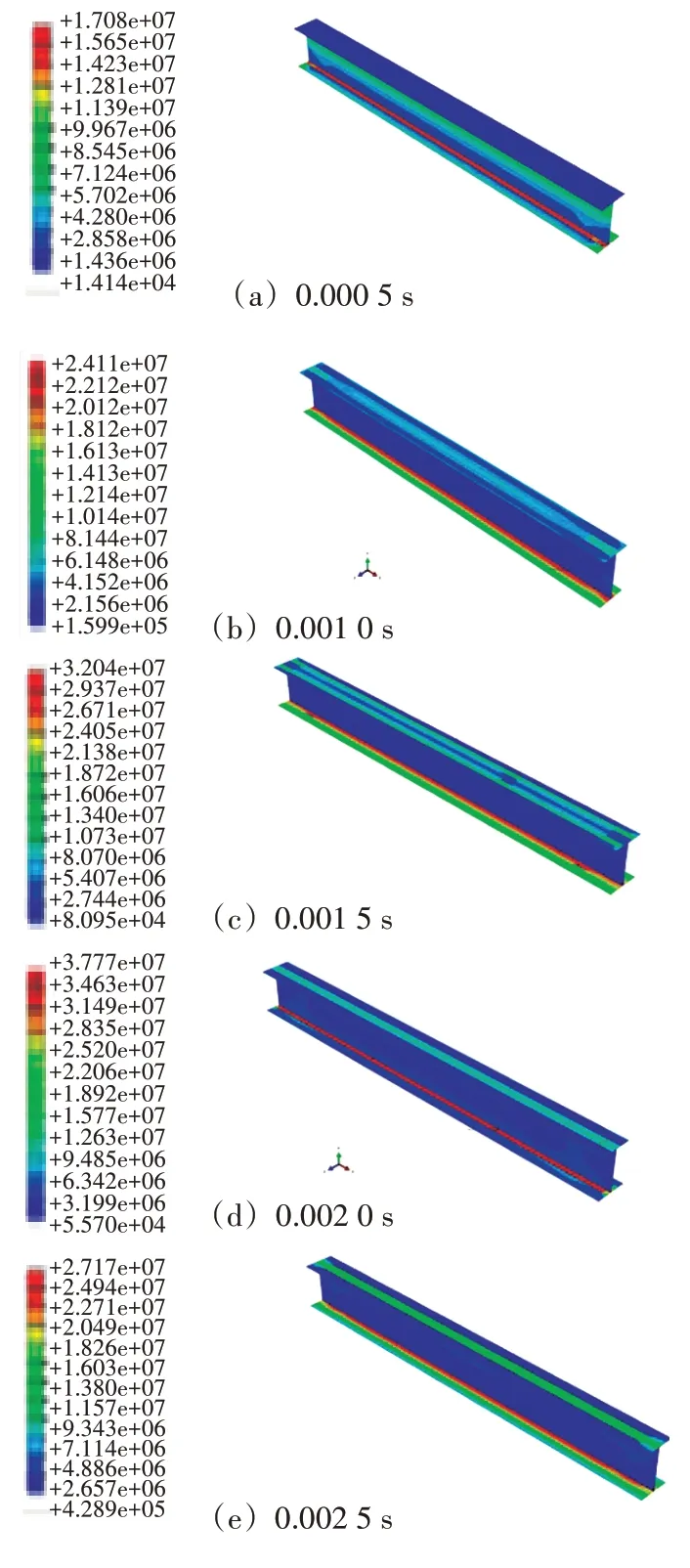
图8 工字梁应力分布

2.4 初始入水速度对最大应力的影响

管汇入水工况的主要参数为初始入水速度，初始入水速度对框架主要工字梁最大应力的影响见图9，最大应力和初始入水速度基本呈线性关系，同时也可看出，H440最大应力稍大于H300。

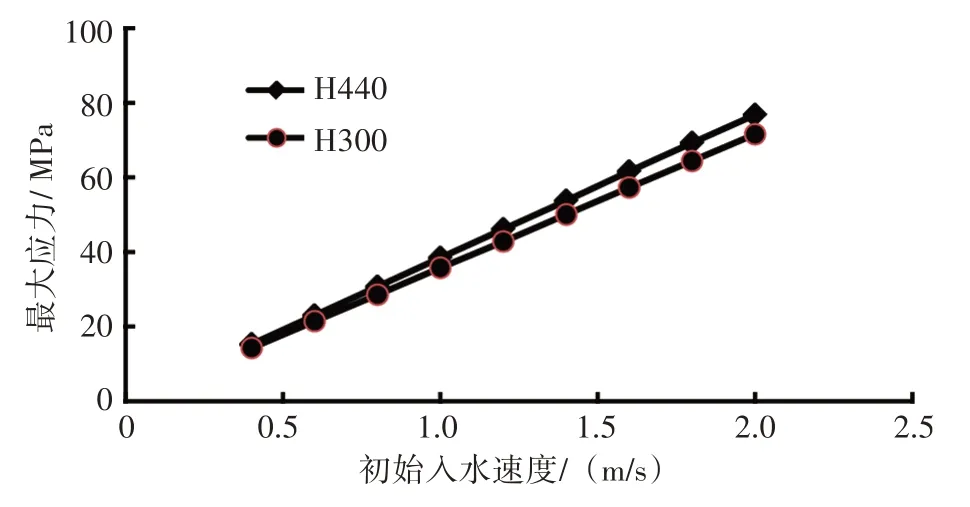
图9 初始入水速度与最大应力的关系

3 结论

本文根据管汇框架入水受力特点，采用耦合欧拉-拉格朗日方法（CEL）模拟了管汇框架主要结构（工字梁）入水过程，给出了工字梁速度-时间历程、应力-时间历程、应力分布图以及入水速度对最大应力的影响，为管汇入水工况安全分析提供了方法支持。